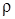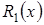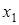АСИМПТОТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ НЕСТАЦИОНАРНЫХ РЕЖИМОВ В СЕТЯХ СЛУЧАЙНОГО ДОСТУПА
(Дипломная работа)
Научный руководитель
д-р тех. наук, профессор
__________
Автор работы
__________
Томск 2002
Содержание
Введение………………………………………………………………………….. 3
1. Исследование нестационарной сети случайного доступа с динамическим протоколом в условиях большой загрузки …………..... 6
2. Исследование неоднородной нестационарной сети случайного
доступа с динамическим протоколом в условиях перегрузки………... 19
3. Исследование нестационарной сети случайного доступа со
статическим протоколом в условиях большой задержки……………... 28
4. Исследование стационарного режима в сети с динамическим протоколом случайного множественного доступа для конечного
числа станций……………………………………………………………. 41
4.1. Асимптотический анализ распределения вероятностей состояний сети……………………………………………………………….... 45
4.2. Численный метод анализа распределения вероятностей………. 52
4.3. Определение области применимости асимптотических формул 55
Заключение…………………………………………………………………….... 60
Список использованной литературы………………………………………….. 62
Введение
В последнее время во многих областях производства возникает необходимость использования процессов распределенной обработки информации, причем на самых различных уровнях: от отдельного учреждения до целой сети предприятий, охватывающей огромные расстояния. Поэтому вполне естественно наблюдаемое ныне бурное развитие сетей связи, позволяющих соединять в единые системы различные устройства вычислительной техники. При этом научные исследования, направленные на улучшение функционирования сетей, ведутся в двух направлениях: повышения физических характеристик канала передачи и создания эффективных сетевых протоколов, позволяющих использовать физические возможности канала оптимальным образом.
При оптимизации и проектировании сетей передачи данных наиболее действенным инструментом является использование математического моделирования. Для того чтобы исследовать уже существующие сети связи специалисты по сетям используют различные анализаторы протоколов, но такие методы не позволяют получать вероятностно-временные характеристики для еще не существующих сетей, находящихся на стадии проектирования. В этих случаях необходимо использовать средства моделирования, с помощью которых разрабатываются адекватные модели, описывающие процессы, протекающие в сетях, и проводится всесторонний анализ этих процессов.
Исследование поведения систем связи из-за случайных влияний возможно только с помощью случайных процессов [1]. Выбор случайных процессов, используемых для описания и анализа систем, зависит от структуры и типа системы, от предположений о независимости или зависимости случайных величин, от вида их функций распределения. Поэтому для исследования таких систем часто используется аппарат теории массового обслуживания [2]. Использование этого аппарата позволяет построить математические модели изучаемой сети связи [3] и провести теоретические исследования параметров функционирования реальной системы.
В классической литературе различают два основных класса систем массового обслуживания [2]: системы с потерями (без очереди) и системы с ожиданиями, а также комбинация этих двух типов – система с ожиданием и потерями (например, система с ограниченным числом мест для ожидания в бункере) [4]. Математические модели спутниковых сетей связи с протоколами случайного множественного доступа формируют третий класс СМО – системы с повторными вызовами. Развитие сетей с множественным доступом началось с появления работы Абрамсона, в которой описано функционирование территориально-распределенных терминалов, соединенных центральной ЭВМ по радиоканалам. Эта система получила название ALOHA. Особенностью протоколов множественного доступа является то, что на множестве станций не вводится изначальной строгой очередности. Каждая станция после появления у нее готового пакета вправе его передавать сразу же, как только обнаружит канал свободным. При этом не исключена возможность, что она попадет в конфликт, то есть ее пакет столкнется с пакетом другой станции. В подобных случаях станция прекращает передачу и генерирует случайную задержку, после которой вновь пытается занять канал.
Асимптотические методы [5] играют важную роль при исследовании различных математических моделей, в том числе таких, которыми описывается функционирование различных типов систем массового обслуживания. Точные формулы для решений удается получить, как правило, лишь в исключительных ситуациях, характеризующихся наложением ограничений на статистическую природу процессов, управляющих системой (таковыми обычно являются входящий поток требований и процесс обслуживания). Однако часто, применяя различные асимптотические методы можно получить удовлетворительное для практики приближенное (асимптотическое) решение задачи при весьма широких предположениях относительно входа и обслуживания даже при отсутствии явного вида распределений характеристик.
Говоря об асимптотических методах, асимптотическом решении и т. д., мы предполагаем, что исследуемая система (или исследуемый процесс, связанный с функционированием системы) характеризуется наличием (одного или нескольких) параметра s, имеющего определенный физический смысл, значение которого близко к некоторому «критическому» значению 
. В каждом конкретном случае параметр s, его предельное значение и характер приближения s к 
имеют вполне определенный смысл, вытекающий из постановки задачи. Часто таким параметром считают время t, и нас интересует поведение тех или иных характеристик СМО в достаточно удаленный от начала момента функционирования системы момент времени. В СМО существенное значение имеет поведение загрузки системы, особенно когда загрузка стремится к критической. Асимптотический метод применяется, если интенсивность повторения заявки в системах с повторными вызовами стремится к нулю. Во всех случаях можно найти асимптотическую плотность распределения вероятностей основных стохастических параметров, обусловливающих функционирование исследуемой системы.
В качестве предельных процессов в теории массового обслуживания чаще других возникают диффузионные марковские процессы [6].
Предложенный метод анализа марковизируемых систем [7] обычно имеет два этапа. На первом этапе удается определить асимптотическое среднее исследуемых характеристик системы, а на втором – распределение вероятностей значений отклонений рассматриваемых характеристик от их асимптотических средних.
Первое приближение
В системе уравнений (2.1) произведем замену переменных: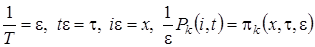 
. В результате такой замены производится переход от дискретной переменной 
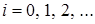к непрерывной переменной 
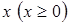, от t перешли к 
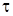, причем 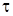такое, что 
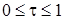. После замены производная равна 
.
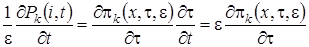Тогда уравнения (2.1) перепишем
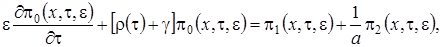
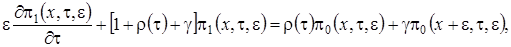(2.2)
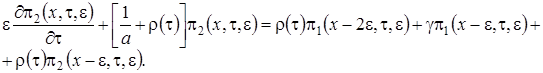
Решим систему уравнений (2.2) в два этапа.
1 этап. Считая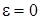 
и предполагая, что 
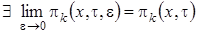будем иметь
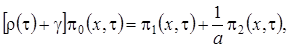
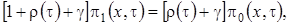(2.3)
.
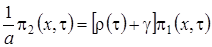Выразим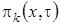 
через функцию 
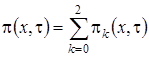и получим
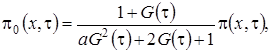
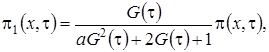(2.4)
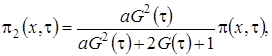
где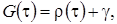 
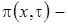асимптотическая плотность распределения нормированного числа заявок в источнике повторных вызовов.
Обозначим
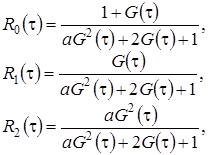(2.5)
( 
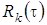- это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Заметим, что из системы (2.3) следуют равенства связывающие 
, 
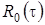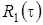и 
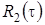
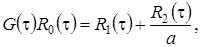
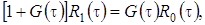(2.6)
.
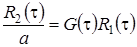Найдем вид функции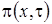 
, для этого перейдем ко второму этапу.
2 этап. В системе дифференциальных уравнений (2.2) все функции с аргументом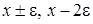 
разложим в ряд по приращению аргумента 
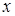, ограничиваясь слагаемыми порядка 
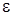, получим
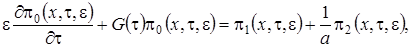
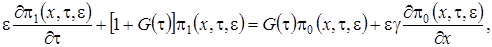(2.7)
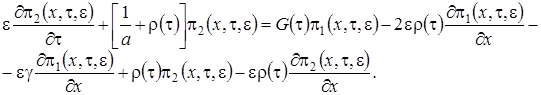
Просуммируем левые и правые части уравнений системы (2.7) и получим равенство
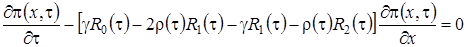. (2.8)
С учетом того, что
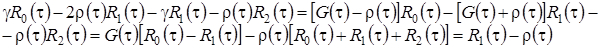
равенство (2.8) принимает вид
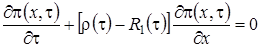. (2.9)
Уравнение (2.9) является однородным линейным уравнением с частными производными первого порядка. Для того чтобы его решить составим уравнение
,
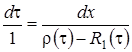его решение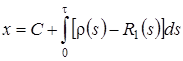 
, тогда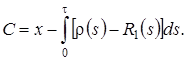 
Общее решение уравнения (2.9) имеет вид
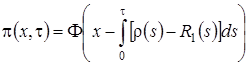, (2.10)
где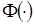 
- произвольная дифференцируемая функция, аналитическое выражение которой найдем из начальных условий.
Пусть распределение в начальный момент времени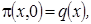 
где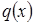 
некоторая плотность распределения. Тогда 
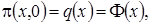следовательно 
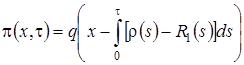. Возьмем в качестве начальной плотности распределения 
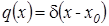, где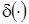 
- дельта-функция Дирака, а 
, 
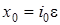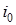- число заявок в источнике повторных вызовов в начальный момент времени.
Таким образом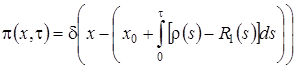 
, из свойств функции Дирака следует, что 
.
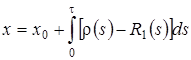То есть мы получили, что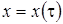 
, 
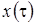имеет смысл асимптотического среднего.
Из приведенных рассуждений вытекает еще одно важное следствие, а именно
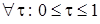имеет место 
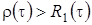, тогда 
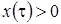(отрицательная функция 
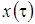противоречит смыслу задачи). В нашем случае 
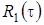совпадает с пропускной способностью системы.
Перейдем ко второму приближению, в котором будем искать распределение отклонения от асимптотического среднего.
Второе приближение
В исходной системе уравнений (2.1) сделаем замену переменных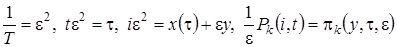 
.
Заметим, что в новых обозначениях производная по времени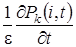 
равна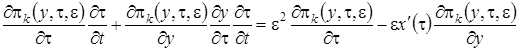 
. С учетом этого система (2.1) примет вид
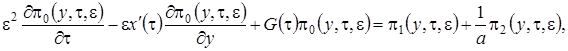
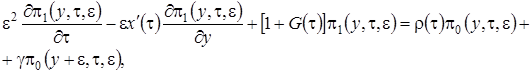(2.11)
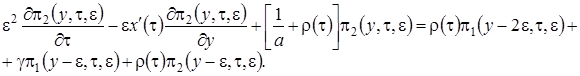
Решение системы уравнений (2.11) аналогично решению системы (2.2), но проводится в три этапа.
1 этап. В системе дифференциальных уравнений (2.13) сделаем предельный переход при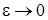 
и предположим, что 
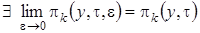, получим
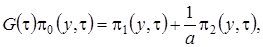
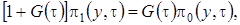(2.12)
.
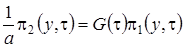Решим эту систему аналогично тому, как решили систему уравнений (2.3). Введем функцию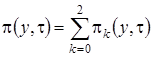 
и выразим через нее 
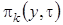, получим
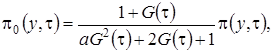
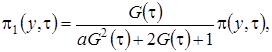(2.13)
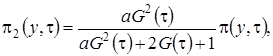
где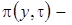 
асимптотическая плотность распределения отклонения числа заявок в источнике повторных вызовов от асимптотического среднего.
2 этап. Функции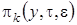 
будем искать с точностью до 
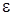в форме
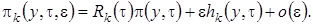(2.14)
Найдем вид функци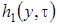й 
, 
и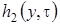 
. Для этого в системе дифференциальных уравнений (2.11) все функции с аргументом 
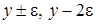разложим в ряд по приращению аргумента 
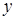, ограничимся слагаемыми порядка 
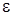. Получим
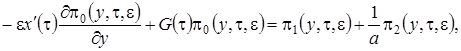
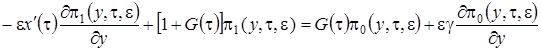(2.15)
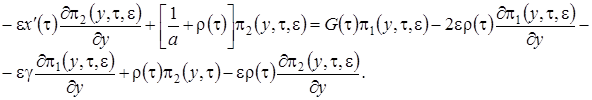
В уравнения (2.15) подставим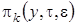 
в форме (2.14), приведем подобные и получим систему неоднородных линейных алгебраических уравнений относительно 
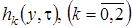вида
,
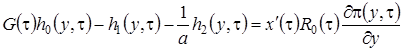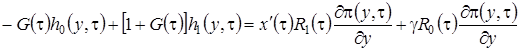, (2.16)
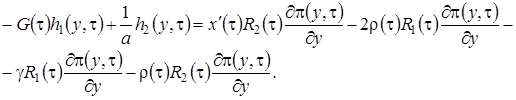
Нетрудно увидеть, что между уравнениями этой системы есть зависимость и ранг матрицы системы равен, следовательно, чтобы решение уравнений (2.16)существовало, необходимо выполнение равенства
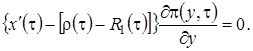(2.17)
Из однородного линейного уравнения с частными производными первого порядка (2.9) мы знаем, что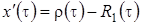 
. Таким образом, можно сделать вывод, что система (2.16) разрешима. При условии, что функция 
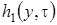известна, решение можно записать в виде
,
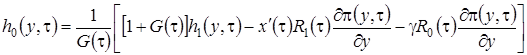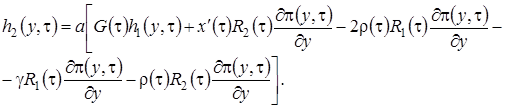(2.18)
Теперь все готово, для того, чтобы найти функцию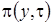 
. Перейдем к третьему этапу.
3 этап. В системе дифференциальных уравнений (2.11) все функции с аргументом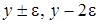 
разложим в ряд по приращению аргумента 
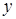, ограничиваясь слагаемыми порядка 
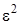, получим
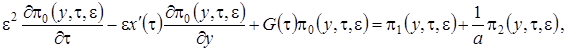
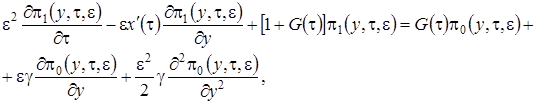(2.19)
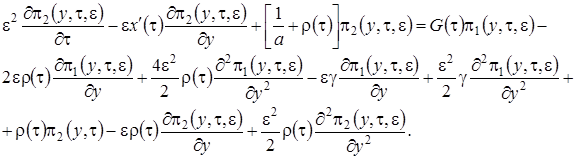
Теперь подставим в уравнения (2.19) 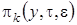в форме (2.14) и просуммируем левые и правые части уравнений, будем иметь
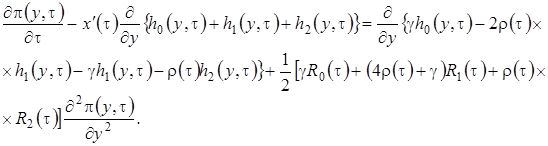(2.20)
Подставляя вместо и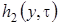 
их выражения, полученные на втором этапе получим для 
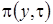уравнение Фоккера-Планка
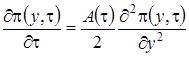, (2.21)
где
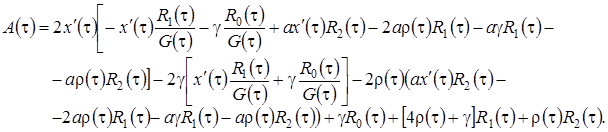
Нормированным решением полученного одномерного уравнения диффузии [8] является плотность нормального распределения вероятностей с нулевым средним и дисперсией
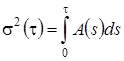. (2.22)
Первое приближение
Для асимптотического решения системы (3.1) сделаем замену переменных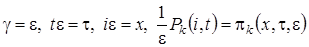 
. В результате замены производится переход от дискретной переменной 
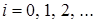к непрерывной переменной 
.
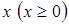В новых обозначениях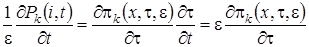 
. Тогда система (3.1) примет вид
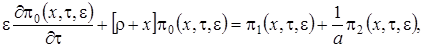
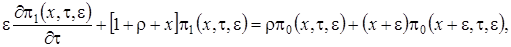(3.2)
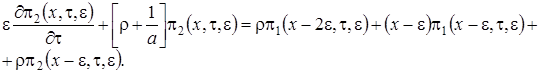
Получим вид решения системы (3.2), которую будем решать в два этапа.
1 этап. Считая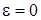 
и предполагая, что 
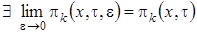, будем иметь
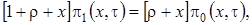(3.3)
.
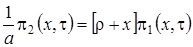Выразим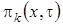 
через функцию 
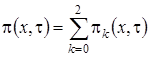и получим
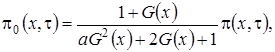
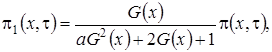(3.4)
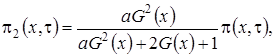
где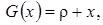 
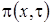- асимптотическая плотность нормированного числа заявок в источнике повторных вызовов.
Обозначим
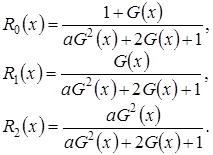(3.5)
Заметим, что из системы (3.3) следуют равенства
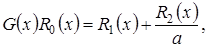
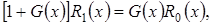(3.6)
.
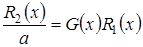Осталось найти вид функции 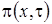. Для этого перейдем ко второму этапу.
2 этап. В системе (3.2) разложим функции по приращению аргумента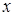 
, ограничиваясь слагаемыми порядка 
, получим систему
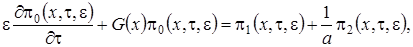
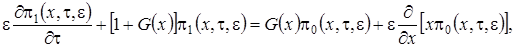(3.7)
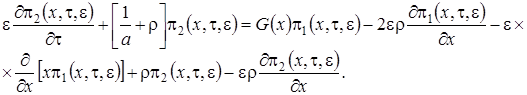
Просуммируем полученные уравнения, поделим на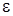 
и перейдем 
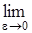. Тогда будем иметь
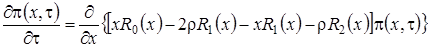. (3.8)
С учетом того, что
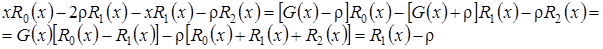
равенство (3.8) принимает вид
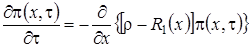. (3.9)
Таким образом мы получили, что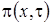 
удовлетворяет уравнению Фоккера-Планка с коэффициентом переноса равным 
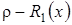, и нулевым коэффициентом диффузии. Из определения для коэффициента переноса можно сделать вывод, что 
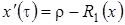, то есть 
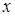зависит от времени и 
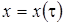– имеет смысл асимптотического среднего, в ее окрестности достаточно долго флуктуируют значения нормированного процесса 
.
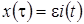Второе приближение
Зная асимптотическое среднее, найдем распределение вероятностей значений отклонения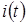 
от его среднего. Для этого в исходной системе уравнений (3.1) сделаем замену переменных 
, 
, 
, 
.
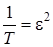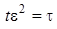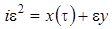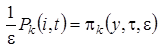В новых обозначениях производная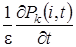 
равна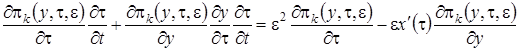 
.
Будем иметь
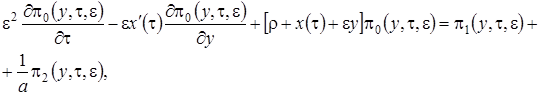
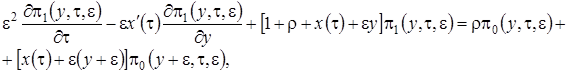(3.10)
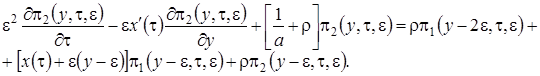
Решение системы (3.10) аналогично решению системы (3.2), но проводится в три этапа.
1 этап. В системе дифференциальных уравнений (3.10) положим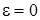 
и найдем решение в виде
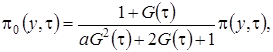
(3.11)
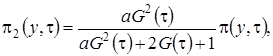
где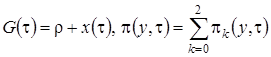 
– асимптотическое распределение нормированного числа заявок в источнике повторных вызовов в окрестности асимптотического среднего.
Перейдем ко второму этапу.
2 этап. Неизвестные функции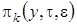 
будем искать с точностью до 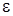форме
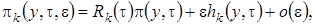(3.12)
где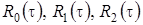 
имеют вид аналогичный (3.5), где в качестве 
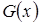выступает 
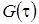и для них справедливы равенства (3.7).
Найдем вид функций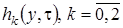 
.
С точностью до 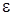(3.10) запишем
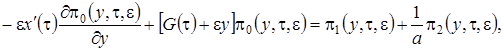
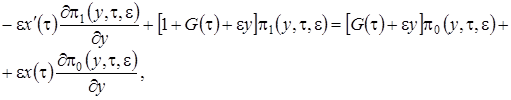(3.13)
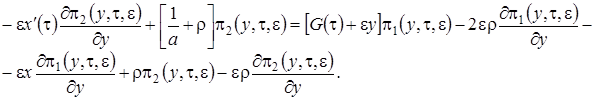
В уравнения (3.13) подставим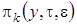 
в форме (3.12), уничтожим подобные слагаемые и получим систему неоднородных линейных алгебраических уравнений относительно функций 
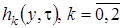вида
,
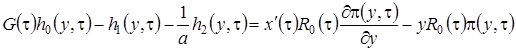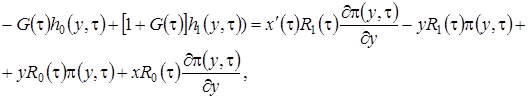, (3.14)
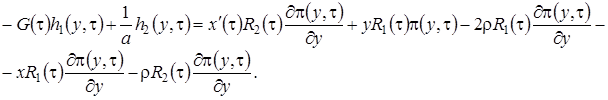
Система (3.14) будет иметь решение, если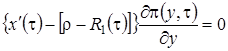 
. Из уравнения Фоккера-Планка (3.9) мы знаем, что 
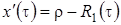. Таким образом, можно сделать вывод, что система (3.14) разрешима. При условии, что функция 
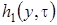известна, решение системы (3.14) можно записать так
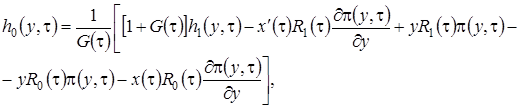(3.15)
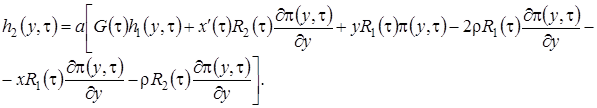
Перейдем к третьему этапу.
3 этап. С точностью до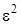 
уравнения (3.10) запишем следующим образом
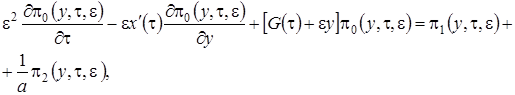
(3.16)
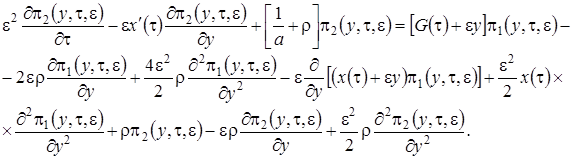
Теперь подставляем в систему уравнений (3.16)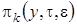 
в форме (3.12), оставляем слагаемые, имеющие порядок не выше 
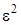и суммируем уравнения. Получим равенство для нахождения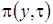 
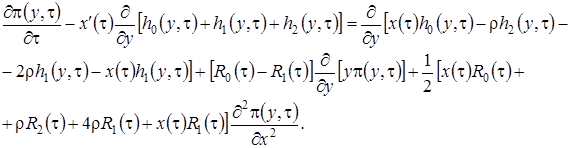(3.17)
В полученное равенство подставим выражения для функци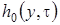и 
и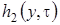 
, найденные на втором этапе. В результате приведения подобных, для 
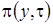получим уравнение Фоккера-Планка
(3.18)
с коэффициентом переноса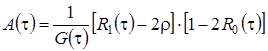 
и коэффициентом диффузии
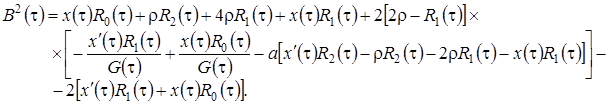
Уравнение Фоккера-Планка (3.18) получено для некоторого диффузионного процесса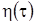 
, плотность распределения вероятностей которого 
.
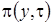Запишем стохастическое дифференциальное уравнение для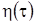 
в общей форме
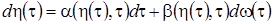, (3.19)
где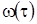 
- винеровский процесс с нулевым средним и единичным коэффициентом диффузии, в нашем случае оно приобретает вид
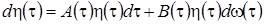. (3.20)
Введем новый случайный процесс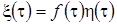 
, (3.21)
для его приращения справедливо
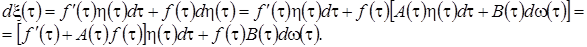
Выберем функцию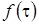 
так, чтобы она удовлетворяла дифференциальному уравнению 
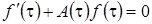. Например, 
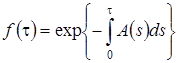. Тогда 
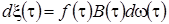и, следовательно, 
.
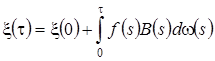Выразим из (3.21) функцию 
(заметим, что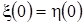 
) и получим
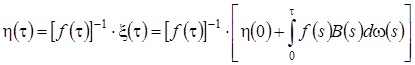(3.22)
Анализируя вид процесса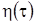 
можно сделать вывод, что он распределен по нормальному закону. Найдем 
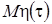и 
, которые полностью определяют вид плотности распределения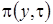 
. Учитывая свойства винеровского процесса, получим
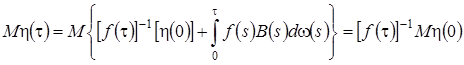(3.23)
Найдем дисперсию.
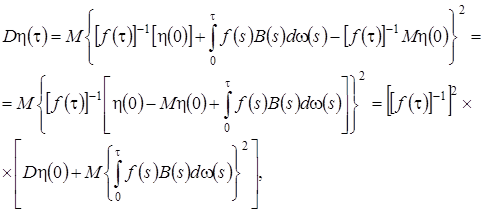
рассмотрим второе слагаемое подробнее. Для этого введем обозначение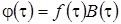 
, тогда получим
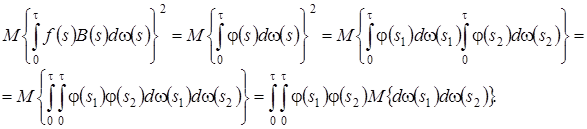
С учетом того, что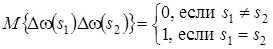 
будем иметь
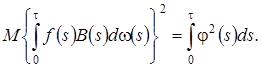
Тогда в окончательном варианте дисперсия равна
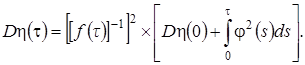(3.24)
Теперь можно записать решение уравнения Фоккера-Планка (3.18), которое имеет вид
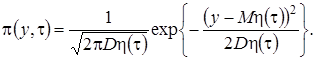(3.25)
Пусть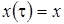 
, где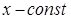 
- точка покоя дифференциального уравнения 
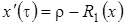, которая определяется конечным уравнением
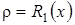, (3.26)
где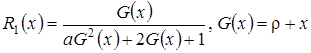 
.
Возможны три варианта:
1. 
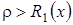, тогда точек покоя не существует (рис. 3.5).
2. 
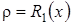, тогда существует одна точка покоя 
.
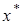3. 
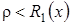, тогда существует две точки покоя 
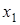и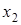 
.
Для примера рассмотрим случай, когда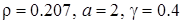 
(рис. 3.6). Тогда уравнение (3.26) имеет единственный корень 
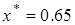. Коэффициенты диффузии уравнения Фоккера-Планка не зависят от времени и равны 
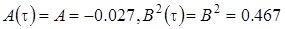. Если взять 
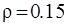, то уравнение (3.26) будет иметь два корня 
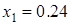и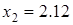 
(рис. 3.7). Для первой точки коэффициенты диффузии равны 
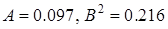, для второй 
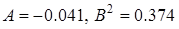. Точка 
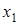является нежелательной. Если предположить, что сеть связи работает в стационарном режиме, то в окрестности точки 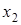распределение нормированного числа заявок в ИПВ является нормальным [1] и имеет вид
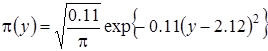, (3.27)
 | |||
| |||
|
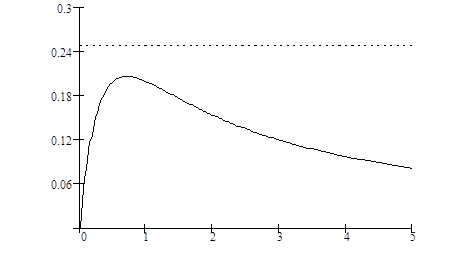
Рис. 3.5
|
|
|
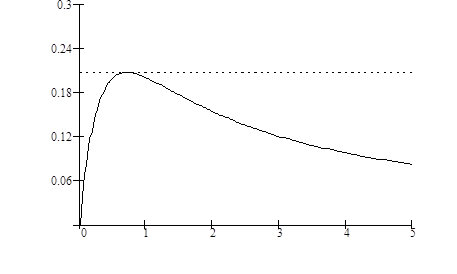
Рис. 3.6
|
|
|
|
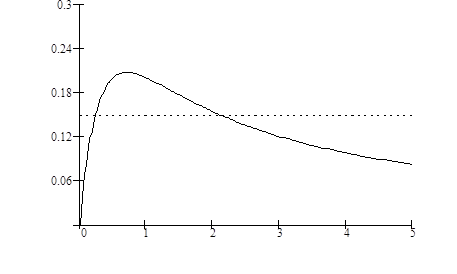
Рис. 3.7
Первое приближение
В системе уравнений (4.1) сделаем следующие замены переменных: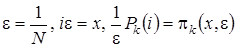 
. В результате такой замены производится переход от дискретной переменной 
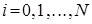к непрерывной переменной 
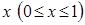. В новых обозначениях система (4.1) примет вид
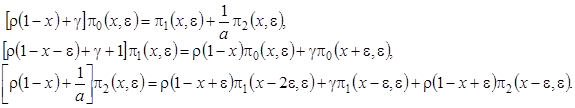(4.2)
Получим вид решения системы (4.2), которую будем решать в два этапа.
1 этап . Устремим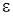 
к нулю и обозначим 
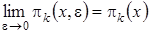. Тогда система (4.2) перейдет в систему
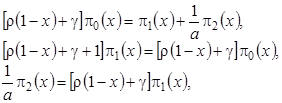(4.3)
решение которой имеет вид
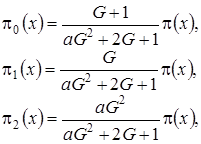(4.4)
где 
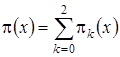– асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.
Осталось найти вид функции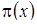 
, для этого перейдем ко второму этапу.
2 этап . В системе (4.2) все функции с аргументом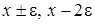 
разложим в ряд по приращению аргумента 
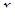, ограничиваясь слагаемыми порядка 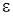, получим
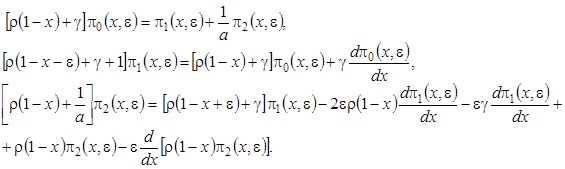(4.5)
Сложив все уравнения системы, будем иметь
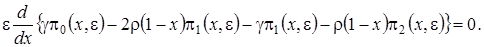(4.6)
В полученном равенстве поделим левую и правую части на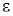 
и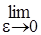 
, прейдем к такому равенству
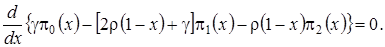(4.7)
Подставим в (4.7) функции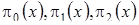 
в форме (4.4) и получим
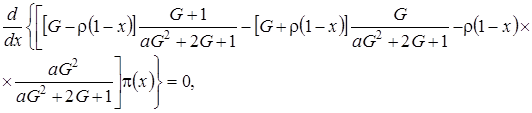(4.8)
следовательно
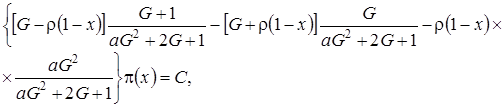(4.9)
где С – некоторая постоянная.
Необходимо найти константу C. Нетрудно заметить, что при х=0 выражение в фигурных скобках не положительно, следовательно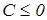 
, а при х=1 
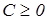. Итак, 
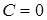. Таким образом, произведение двух функций равно нулю, следовательно, 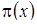может принимать какое-либо ненулевое значение лишь в тех точках, в которых выражение в скобках равно нулю.
Получим функцию 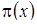, везде равную нулю, за исключением точек, являющихся корнями уравнения
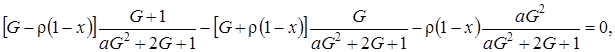
после преобразований это выражение принимает вид
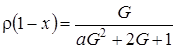(4.10)
Так как 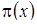– плотность распределения вероятностей, то должно выполняться условие нормировки 
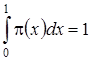. Этим условиям удовлетворяет лишь функция вида
,
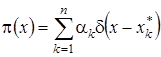где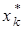 
– корни уравнения (4.10), n – число корней, 
.
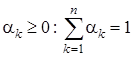Если уравнение (4.10) имеет единственный корень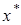 
, то эту точку назовем точкой стабилизации, потому что она является модой распределения вероятностей нормированного процесса заявок в ИПВ 
, и в ее окрестности достаточно долго флуктуируют значения этого процесса. В этом случае назовем сеть моностабильной.
Второе приближение
Пусть уравнение (4.10) имеет единственный корень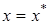 
, то есть плотность распределения исследуемой сети сосредоточена около точки 
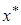. Найдем плотность распределения отклонения от этой точки. Для этого в системе (4.1) сделаем замену переменных: 
, 
, 
.
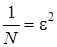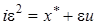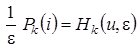В новых обозначениях система (4.1) примет вид
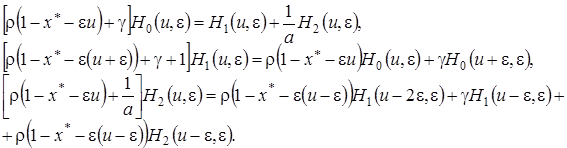(4.11)
Систему (4.11) будем решать в три этапа.
1 этап. Устремим 
к нулю и обозначим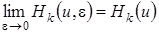 
, тогда система (4.11) перейдет в систему
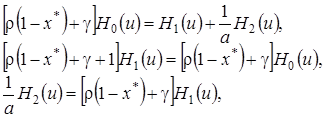(4.12)
решение которой имеет вид
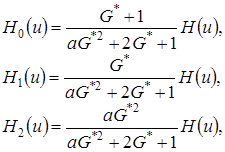(4.13)
где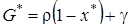 
, 
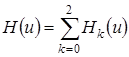– плотность распределения нормированной величины 
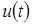отклонения процесса 
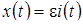от значения 
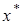– корня уравнения (4.10).
Найдем вид функции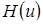 
.
2 этап. Неизвестные функции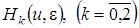 
будем искать в форме
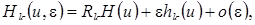(4.14)
где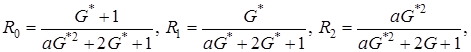 
(4.15)
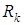– асимптотическая вероятность того, что состояние обслуживающего канала равно 
.
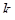В системе уравнений (4.11) все функции с аргументом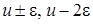 
разложим в ряд по приращению аргумента 
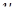, ограничиваясь слагаемыми порядка 
, получим
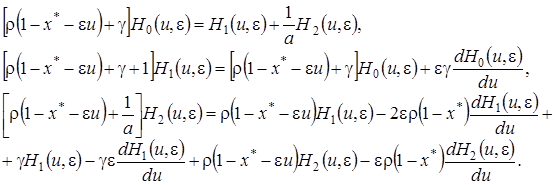(4.16)
В полученных формулах заменяем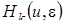 
по формуле (4.14), при этом учитываем, что из системы (4.12) следуют равенства
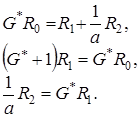(4.17)
Получим неоднородную линейную систему алгебраических уравнений относительно неизвестных функций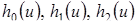 
(в предположении, что 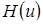известна) вида
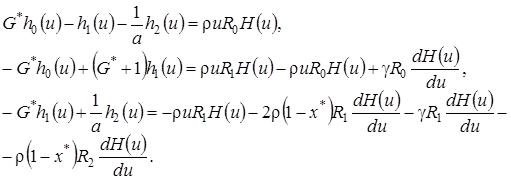(4.18)
Заметим, что ранг соответствующей однородной системы равен двум. Следовательно, для того, чтобы решение системы (4.18) существовало, необходимо, чтобы ранг расширенной матрицы этой системы также равнялся двум, т.е. чтобы выполнялось следующее равенство
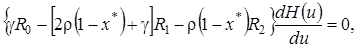(4.19)
откуда следует, что
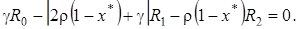(4.20)
Чтобы показать равенство (4.20) воспользуемся определением для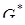 
и свойствами констант 
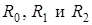, получим
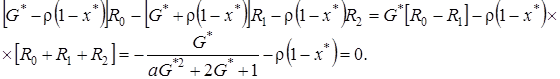(4.21)
Если предположить, что функция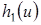 
известна, то решение системы (4.18) примет вид
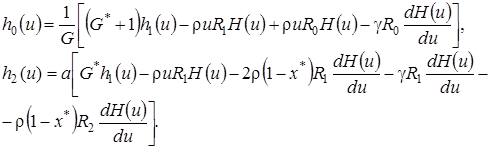(4.22)
3 этап. В системе (4.11) все функции с аргументом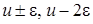 
разложим в ряд по приращению аргумента 
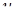, ограничиваясь слагаемыми порядка 
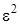, будем иметь
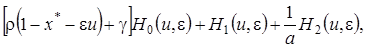
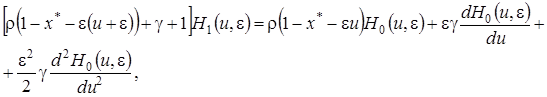(4.23)
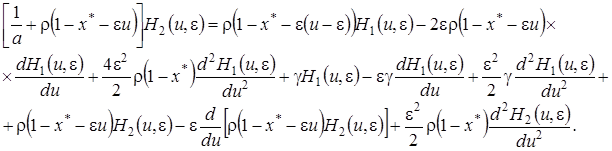
Сложив левые и правые части системы уравнений (4.23) получим
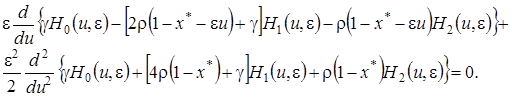(4.24)
Чтобы сделать предельный переход в полученной формуле, нужно чтобы все слагаемые имели порядок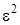 
. Заменим 
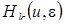по формуле (4.14), подставив вместо 
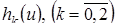их выражения, полученные на втором этапе. Для 
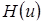получим линейное дифференциальное уравнение второго порядка вида
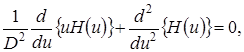(4.25)
где
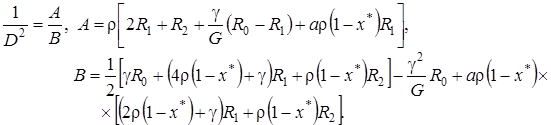(4.26)
Решение уравнения (4.25) можно найти в виде
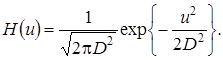(4.27)
Заключение
В данной работе проведено исследование функционирования нестационарных сетей связи случайного доступа с оповещением о конфликте для конечного и бесконечного числа абонентских станций. Рассмотрен динамический и статический протокол случайного множественного доступа.
В первом разделе проведено исследование нестационарной сети случайного доступа с динамическим протоколом в условиях большой загрузки. Определена точная верхняя граница загрузки сети, при которой существует стационарный режим. Исследование показало, что плотность распределения нормированного числа заявок в источнике повторных вызовов удовлетворяет уравнению Фоккера-Планка с постоянными коэффициентами. Предложен метод его решения с помощью преобразования Лапласа.
Во втором разделе проведено исследование неоднородной нестационарной сети случайного доступа с динамическим протоколом в условиях перегрузки. В первом приближении получено асимптотическое среднее, во втором распределение отклонения в окрестности асимптотического среднего, которое удовлетворяет уравнению Фоккера-Планка с нулевым коэффициентом переноса и является нормальным.
В третьем разделе проведено исследование нестационарной сети случайного доступа со статическим протоколом в условиях большой задержки. В первом приближении получено асимптотическое среднее, во втором распределение отклонения в окрестности асимптотического среднего, которое удовлетворяет уравнению Фоккера-Планка и является нормальным. Рассмотрены точки покоя.
В четвертом разделе исследовано функционирование сети случайного множественного доступа с динамическим протоколом для конечного числа абонентских станций. В п. 4.1. изложены два этапа асимптотического анализа. На первом этапе удалось определить асимптотическую «предельную» точку, в окрестности которой «концентрируется» искомая плотность распределения вероятности, а на втором этапе – нашли распределение отклонения в окрестности «предельной» точки. На этом этапе получено асимптотически нормальное распределение, что является аналогом известных в теории вероятностей законов больших чисел и центральных предельных теорем. Особенностью рассматриваемой СМО, является то, что алгебраические уравнения, описывающие ее функционирование, имеют точное численное решение, которое изложено в п. 4.2. Поэтому в п. 4.3. проводится аналогия между численным и асимптотическим решением и определяется область применимости асимптотических формул.
Список использованной литературы
1. Радюк Л.Е., Терпугов А. Ф. Теория вероятностей и случайных процессов – учебное пособие. Томск: Издательство Томского университета, 1988.
2. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. М: Наука, 1987.
3. Клейнрок Л. Вычислительные системы с очередями. М: Мир, 1979.
4. Кениг Д., Штоян Д. Методы теории массового обслуживания. М: Радио и связь, 1981.
5. Боровков А. А. Асимптотические методы в теории массового обслуживания. М: Наука, 1980.
6. Гихман И. И., Скороход А. В. Стохастические дифференциальные уравнения. Киев: Наукова думка, 1968.
7. Назаров А. А. Асимптотический анализ марковизируемых систем. Томск: Издательство Томского университета, 1991.
8. Араманович И. Г., Левин В. И. Уравнения математической физики. М: Наука, 1969.
9. Саати Т. Л. Элементы теории массового обслуживания и ее приложения .М: Советское радио, 1971.
10. Климов Г.П. Стохастические системы обслуживания. М: Наука, 1966.
11. Ги К. Введение в локальные вычислительные сети. М: Радио и связь, 1986.
12. Бертсекас Д., Галлагер Р. Сети передачи данных. М: Мир, 1989.
13. Баруча-Рид А. Т. Элементы теории марковских процессов и их приложения. М: Наука, 1969.
14. Шохор С. Л. Математические модели локальных вычислительных сетей с динамическими протоколами случайного множественного доступа и их исследование//Автореферат диссертации. Томск, 2001.
15. Одышев Ю. Д. Исследование сетей связи, управляемых протоколом случайного множественного доступа «Адаптивная АЛОХА»//Автореферат диссертации. Томск, 2001.
16. Туенбаева А. Н. Исследование математических моделей сетей связи со статическими протоколами случайного множественного доступа//Автореферат диссертации. Томск, 2001.
АСИМПТОТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ НЕСТАЦИОНАРНЫХ РЕЖИМОВ В СЕТЯХ СЛУЧАЙНОГО ДОСТУПА
(Дипломная работа)
Научный руководитель
д-р тех. наук, профессор
__________
Автор работы
__________
Томск 2002
Содержание
Введение………………………………………………………………………….. 3
1. Исследование нестационарной сети случайного доступа с динамическим протоколом в условиях большой загрузки …………..... 6
2. Исследование неоднородной нестационарной сети случайного
доступа с динамическим протоколом в условиях перегрузки………... 19
3. Исследование нестационарной сети случайного доступа со
статическим протоколом в условиях большой задержки……………... 28
4. Исследование стационарного режима в сети с динамическим протоколом случайного множественного доступа для конечного
числа станций……………………………………………………………. 41
4.1. Асимптотический анализ распределения вероятностей состояний сети……………………………………………………………….... 45
4.2. Численный метод анализа распределения вероятностей………. 52
4.3. Определение области применимости асимптотических формул 55
Заключение…………………………………………………………………….... 60
Список использованной литературы………………………………………….. 62
Введение
В последнее время во многих областях производства возникает необходимость использования процессов распределенной обработки информации, причем на самых различных уровнях: от отдельного учреждения до целой сети предприятий, охватывающей огромные расстояния. Поэтому вполне естественно наблюдаемое ныне бурное развитие сетей связи, позволяющих соединять в единые системы различные устройства вычислительной техники. При этом научные исследования, направленные на улучшение функционирования сетей, ведутся в двух направлениях: повышения физических характеристик канала передачи и создания эффективных сетевых протоколов, позволяющих использовать физические возможности канала оптимальным образом.
При оптимизации и проектировании сетей передачи данных наиболее действенным инструментом является использование математического моделирования. Для того чтобы исследовать уже существующие сети связи специалисты по сетям используют различные анализаторы протоколов, но такие методы не позволяют получать вероятностно-временные характеристики для еще не существующих сетей, находящихся на стадии проектирования. В этих случаях необходимо использовать средства моделирования, с помощью которых разрабатываются адекватные модели, описывающие процессы, протекающие в сетях, и проводится всесторонний анализ этих процессов.
Исследование поведения систем связи из-за случайных влияний возможно только с помощью случайных процессов [1]. Выбор случайных процессов, используемых для описания и анализа систем, зависит от структуры и типа системы, от предположений о независимости или зависимости случайных величин, от вида их функций распределения. Поэтому для исследования таких систем часто используется аппарат теории массового обслуживания [2]. Использование этого аппарата позволяет построить математические модели изучаемой сети связи [3] и провести теоретические исследования параметров функционирования реальной системы.
В классической литературе различают два основных класса систем массового обслуживания [2]: системы с потерями (без очереди) и системы с ожиданиями, а также комбинация этих двух типов – система с ожиданием и потерями (например, система с ограниченным числом мест для ожидания в бункере) [4]. Математические модели спутниковых сетей связи с протоколами случайного множественного доступа формируют третий класс СМО – системы с повторными вызовами. Развитие сетей с множественным доступом началось с появления работы Абрамсона, в которой описано функционирование территориально-распределенных терминалов, соединенных центральной ЭВМ по радиоканалам. Эта система получила название ALOHA. Особенностью протоколов множественного доступа является то, что на множестве станций не вводится изначальной строгой очередности. Каждая станция после появления у нее готового пакета вправе его передавать сразу же, как только обнаружит канал свободным. При этом не исключена возможность, что она попадет в конфликт, то есть ее пакет столкнется с пакетом другой станции. В подобных случаях станция прекращает передачу и генерирует случайную задержку, после которой вновь пытается занять канал.
Асимптотические методы [5] играют важную роль при исследовании различных математических моделей, в том числе таких, которыми описывается функционирование различных типов систем массового обслуживания. Точные формулы для решений удается получить, как правило, лишь в исключительных ситуациях, характеризующихся наложением ограничений на статистическую природу процессов, управляющих системой (таковыми обычно являются входящий поток требований и процесс обслуживания). Однако часто, применяя различные асимптотические методы можно получить удовлетворительное для практики приближенное (асимптотическое) решение задачи при весьма широких предположениях относительно входа и обслуживания даже при отсутствии явного вида распределений характеристик.
Говоря об асимптотических методах, асимптотическом решении и т. д., мы предполагаем, что исследуемая система (или исследуемый процесс, связанный с функционированием системы) характеризуется наличием (одного или нескольких) параметра s, имеющего определенный физический смысл, значение которого близко к некоторому «критическому» значению . В каждом конкретном случае параметр s, его предельное значение и характер приближения s к имеют вполне определенный смысл, вытекающий из постановки задачи. Часто таким параметром считают время t, и нас интересует поведение тех или иных характеристик СМО в достаточно удаленный от начала момента функционирования системы момент времени. В СМО существенное значение имеет поведение загрузки системы, особенно когда загрузка стремится к критической. Асимптотический метод применяется, если интенсивность повторения заявки в системах с повторными вызовами стремится к нулю. Во всех случаях можно найти асимптотическую плотность распределения вероятностей основных стохастических параметров, обусловливающих функционирование исследуемой системы.
В качестве предельных процессов в теории массового обслуживания чаще других возникают диффузионные марковские процессы [6].
Предложенный метод анализа марковизируемых систем [7] обычно имеет два этапа. На первом этапе удается определить асимптотическое среднее исследуемых характеристик системы, а на втором – распределение вероятностей значений отклонений рассматриваемых характеристик от их асимптотических средних.
Дата: 2019-07-24, просмотров: 186.
