ГЛАВА I . ОРГАНИЗАЦИЯ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКАХ МАТЕМАТИКИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

ДИПЛОМНАЯ РАБОТА

Организация познавательной деятельности учащихся

на факультативных занятиях по теме

«Иррациональные неравенства»

Выполнила: студентка

VI курса МФ

Филиппова Ольга

Владимировна

Научный руководитель:

Кузьмичев Анатолий

Иванович

старший преподаватель

Кафедры алгебры

Г.НОВОСИБИРСК

Г.

СОДЕРЖАНИЕ

Введение.

Глава 1. Организация познавательной деятельности на факультативных занятиях.

1. История развития форм обучения. Сущность понятия “форма” организации познавательной деятельности.

2. Самостоятельная работа учащихся - один из важнейших способов организации познавательной деятельности.

3. Фронтальная и групповая формы организации познавательной деятельности учащихся.

4. Оптимальное сочетание и взаимодействие форм учебно-познавательной деятельности.

Выводы по 1-й главе.

Глава 2. Анализ опытно-экспериментальной работы по применению самостоятельной работы учащихся и других форм познавательной деятельности на факультативных занятиях в выпускных классах.

1. Изучение учебных возможностей учащихся. Методика организации факультативных занятий.

2. Результаты опытно-экспериментальной работы.

Выводы по 2-й главе.

Глава 3. Иррациональные неравенства, способы их решения.

1. Краткие исторические сведения.

2. Неравенства и их основные свойства.

3. Корень n-ой степени. Иррациональные неравенства.

4. Решение простейших иррациональных неравенств.

1-2

3-6

7-10

11-12

13-15

17-21

22-23

25-27

28-38

39-40

41-48

5. Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов чётной степени.

6. Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечётной степени.

7. Решение иррациональных неравенств с параметрами.

8. Решение иррациональных неравенств, способом ведения новой переменной.

9. Способ домножения обеих частей иррационального неравенства на некоторое число, либо выражение.

10. Метод выделения полного квадрата в подкоренных выражениях при решении иррациональных неравенств, либо разложения подкоренного выражения на множители.

11. Решение иррациональных неравенств путём проб, выводов.

12. Решение более сложных примеров.

13. Подборка задач по теме «Решение иррациональных неравенств».

14. Классические неравенства.

Заключение.

Литература.

Приложение.

1. Введение.

2. Разработка факультатива по теме «Иррациональные неравенства».

49-53

54-59

60-65

66-71

72-74

75-77

79-81

83-97

99-100

101-103

104-133

ВВЕДЕНИЕ.

Вспомним, с каким интересом ребёнок первый раз идёт в школу, ведь его ждёт там много нового и неизведанного, интересного и необычного. Но проходит время и интерес к учению пропадает, исчезает желание идти в школу, на уроки, не хочется делать домашнего задания. Неинтересные, однообразные уроки, построенные по одной схеме, повторяющиеся изо дня в день, из урока в урок, быстро надоедают. Почему это происходит? В современной дидактике основное внимание уделяется проблемам, связанным с содержанием обучения и его методами, а самой организации познавательной деятельности учащихся уделяется гораздо меньше внимания, от этого и идёт неумения учителя организовать деятельность учащихся на уроке, незнание учителя как это сделать.

Для того чтобы интерес к учению не пропал, чтобы ученики хотели, а главное умели получать знания, необходимо активизировать деятельность самих учащихся на уроке. Учебный процесс должен строиться так, чтобы ученики сами получали знания, а учитель являлся бы организатором этой деятельности. Учитель должен применять различные формы организации познавательной деятельности, варианты их оптимального сочетания.

Цель дипломной работы – показать эффективность самостоятельной работы учащихся на факультативе при изучении темы «Иррациональные неравенства» в выпускных классах средней школы.

В ходе дипломной работы была выдвинута рабочая гипотеза: самостоятельная работа учащихся является одной из эффективнейших форм обучения, способствует лучшему усвоению знаний, развитию навыков и умений по применению этих знаний, повышает уровень активности учащихся.

В соответствии с целью и принятой гипотезой были выдвинуты следующие задачи:

1. Изучение психолого-педагогической литературы по данной теме.

2. Характеристика и анализ самостоятельной работы учащихся.

3. Изучение учебных возможностей учащихся на факультативе.

4. Проведение опытно-экспериментальной работы в выпускных классах средней школы № 9 г. Куйбышева НСО.

Выполнение задач осуществлялось следующими методами:

1. Анализ психолого-педагогической литературы;

2. Наблюдение;

3. Анкетирование учащихся;

4. Беседы с учащимися;

5. Проведение опытно-экспериментальной работы.

Самостоятельная работа учащихся - один из важнейших способов организации познавательной деятельности.

В учебной деятельности важно, чтобы учащиеся учились не просто запоминать то, что говорит учитель, не просто учили то, что им объясняет учитель, а сами, самостоятельно, могли добывать знания, важно на сколько самостоятелен ученик в усвоении знаний и формировании умений. В этом учителю помогает индивидуальная форма познавательной деятельности. Индивидуальная форма работы учащихся заключается в том, что весь процесс обучения, прежде всего, определяется индивидуальной работой учителя с учеником, либо учащийся самостоятельно выполняет учебное задание на основе рекомендаций и инструкций, полученных от учителя, в соответствии со своими индивидуальными возможностями, без взаимодействия с другими учениками.

Неравномерность усвоения знаний, умений и навыков учащимися одного класса связана с наличием значительных индивидуальных различий среди детей. Всякое общее человек усваивает индивидуально в зависимости от воспитания, жизненных условий, от темперамента и т. д.. Работая самостоятельно, ученик проявляет инициативу, его темп работы зависит от его работоспособности, склонностей, учебных возможностей, подготовленности, целеустремлённости. Такая форма работы предполагает подбор приёмов и дидактических средств обучения, которые обеспечат оптимальное развитие любого ученика в классе, как самостоятельного сильного, так и слабого.

Главный признак индивидуальной формы работы - выполнение «своего» задания. Индивидуальное задание отличается от фронтального тем, что оно подбирается не для всех вместе, а для каждого в отдельности, с учётом индивидуальных особенностей школьника.

Самостоятельность - качество, которое необходимо воспитывать у учащихся. В жизни каждого человека есть ситуации, когда всё приходиться решать самому и переложить на другого нет возможности. Чтобы не растеряться, чтобы быть в состоянии самостоятельно принимать решения - для этого в процессе обучения нужно создавать такие ситуации, где бы ребята без чьей бы то ни было помощи могли решать предложенные познавательные задачи, сами могли изучить материал и рассказать товарищам, сами могли составить задачу и решить её.

Самостоятельная работа учащихся - это работа, которая выполняется без непосредственного участия учителя. Существуют специальные задания, ориентирующие школьников на их самостоятельное выполнение: работа над учебниками, решение задач, написание рефератов, изложений и сочинений и т. д..

Выделяют 4 разновидности самостоятельной, познавательной деятельности в процессе обучения:

1. Цель и план работы ученик осуществляет с помощью учителя;

2. Цель учащийся определяет с помощью учителя, а план - самостоятельно;

3. Цель и план учащийся определяет самостоятельно, но задание даёт учитель;

4. Без помощи учителя учащийся сам определяет содержание, цель, план работы и самостоятельно её выполняет.

Первая разновидность наиболее простая, и с неё учитель должен начинать подготовку ребят к более сложным этапам самостоятельной работы. Затем постепенно, переходя от этапа к этапу, самостоятельная работа «становится всё более «самостоятельной», где ученик может полностью проявлять свои знания, инициативу, личные качества и индивидуальные особенности.

Самостоятельная работа организуется с помощью индивидуальных форм обучения.

Ученик работает самостоятельно дома при выполнении домашних заданий, написании рефератов и т. д.

Индивидуальная форма предполагает деятельность ученика по выполнению общих для всего класса заданий без контакта с одноклассниками, в едином для всех темпе.

Она преимущественно используется при закреплении знаний, формировании умений и навыков, контроле знаний.

Индивидуальная работа на уроке требует от учителя тщательной подготовки, большой затраты сил и времени. Однако эта форма организации познавательной деятельности не всегда создаёт условия для полной самостоятельной деятельности учащихся. Она является хорошим средством организации деятельности сознательных учеников. Но нередко можно наблюдать на уроках картину, когда слабо успевающие учащиеся либо ничем не занимаются, т. к. не могут справиться самостоятельно с заданием, либо спрашивают у соседей по парте о способе решения, что ведёт к списыванию и подсказкам.

Для организации большей самостоятельности школьников используется индивидуализированная форма обучения. Эта форма предполагает такую организацию работы, при которой каждый ученик выполняет своё, отличное от других, задание с учётом учебных возможностей. Дифференцированные индивидуальные задания бывают различной глубины и степени трудности - от простых, на восприятие по образцу, до творческих. Эти задания оформляются на специальных карточках. В начальных классах широкое применение получили тетради с печатной основой. Эта форма организации познавательной деятельности требует от учителя много дополнительных затрат времени и знаний для приготовления карточек, подбора заданий. Сейчас в помощь учителю выпускается специальная методическая литература, где печатаются различные работы нескольких вариантов. Чаще всего индивидуализированная форма обучения применяется с целью проверки степени усвоения учащимися материала.

Индивидуализированная форма учебной деятельности, способствуя воспитанию самостоятельности учеников, таит в себе недостатки. Она разъединяет школьников, создаёт условия для развития эгоизма, снижает положительное влияние на формирование и развитие коллектива, учащийся может замыкаться в себе, становиться малообщительным человеком. Чтобы этого избежать, необходимо включать эту форму в процесс обучения как вспомогательную на продолжительное время.

Нередко встречаются ученики, которые усваивают учебный материал после неоднократного разбора. По этой причине на уроке необходимо находить время для повторного разбора.

Индивидуализированно-групповая форма является дополнительной. Благодаря ей учитель имеет возможность на отдельных этапах урока специально заниматься с 1-2 учениками, не отрывая класс от работы по выполнению общего задания. Эта форма способствует предупреждению отставания слабых и создаёт лучшие условия для развития и повышения своего уровня знаний одарённых школьников. Эта форма организации познавательной деятельности учащихся на уроке может применяться при изучении нового материала, при проверке выполнения домашнего задания, при контроле знаний. Организация индивидуализированно-групповой работы требует высокого мастерства учителя, который должен уметь распределять внимание, использовать разнообразный дидактический материал, работая с отдельными учениками, преподаватель не должен выпускать из вида всех учащихся класса, всё, что происходит на уроке, должно быть в поле его зрения.

Деятельности.

Любая форма учебно-понавательной деятельности имеет свои преимущества и недостатки, выбор той или иной формы обусловлен рядом обстоятельств. В частности, необходимо учитывать специфику изучаемого предмета, его сложность, материал может иметь разную сложность, разную новизну. Трудный материал, обладающий большой степенью новизны на первом этапе, требует фронтальная работы, где главная роль в изложении принадлежит учителю. Подготовленность учащихся и их индивидуальные особенности, квалификация учителя- всё это влияет на выбор той или иной формы организации деятельности учащихся. Сочетание различных форм многовариантно. Оно осуществляется либо последовательно, когда одна форма следует за другой, либо параллельно, когда сочетание протекает одновременно и формы работы входят одна в другую.

Как показывает опыт и множество экспериментов, проведённых различными педагогами, сочетание форм организации деятельности следует применять, идя от сочетания простых, к более сложным, учитывая возраст учащихся, специфику предмета. Для определения оптимального варианта организации деятельности необходимо знать, как влияет конкретная форма на эффективность учебной деятельности различных групп учащихся. «Такое сочетание форм учебной работы, при котором нейтрализуются недостатки одних и обеспечивается более высокая результативность других при минимальных затратах времени, является оптимальным». (Чередов И.М. «Методика планирования школьных форм организации обучения»).

«Оптимальным вариантом сочетания коллективной, групповой и индивидуальной форм работы учащихся будет тот, который в соответствии с дидактической целью и спецификой учебного материала создаёт наилучшие условия для обучения и воспитания». (Виноградова М.Д., Первин И.В. «Коллективная познавательная деятельность и воспитание школьников»).

Выбор формы зависит от многих факторов, но в большей степени от этапа в процессе обучения. Педагоги, которые занимаются этим вопросом, выявили некоторые закономерности и разработали рекомендации по выбору оптимального сочетания форм работы учеников на уроке.

При ознакомлении с новым материалом:

Специфика учебного материала.	Метод учебной работы.	Форма учебной работы.
Материал лёгкий, доступный для самостоятельного обучения.	Самостоятельная работа с учебником, книгой.	И+Ф
Материал труден некоторым учащимся или доступен , но велик по объёму.	Объяснение, беседа, самостоятельная работа.	Ф+Г
Материал трудный или велик по объёму, или неполно освещён в учебнике.	Объяснение, рассказ, лекции, демонстрация.	Ф+И+Ф или Ф+Г+Ф

При закреплении и применении знаний:

Материал лёгкий, доступный для самостоятельного обучения.	Самостоятельная работа, упражнения, лабораторная или практическая работа.	И+Ф
Материал представляет трудность для отдельных учеников.	Самостоятельная работа, лаборатор., практические занятия.	И+Г или Г+Ф
Материал трдный, усвоение требует постоянного руководства учителя.	Упражнения с коментариями, объяснение.	Ф+Г+Ф или Ф+И+Ф

При опросе и проверке знаний:

Материал хорошо усвоен всеми учащимися класса.	Фронтальный опрос, общеклассная контрольная работа.	Ф
Материал недостаточно усвоен отдельными учениками.	Самостоятельная работа по вариантам с учётом уровня знаний.	Г+Ф
Материал сложен, большой по объёму, требует глубокого осмысления, анализа, синтеза.	Индивидуальный опрос с его коллективным обсуждением.	И+Ф

Конечно, эти рекомендации не являются идеальными для всех случаев, они требуют определённой корректировки и доработки в конкретных условиях, на конкретном уроке и предмете.

Выводы по 1-й главе:

В первой главе дипломной работы исследуется теоретическая сторона данной проблемы, характеризуется самостоятельная работа учащихся, другие формы организации познавательной деятельности, раскрывается история развития форм обучения с древнейших времён до наших дней. Существуют три основные формы организации учебно-познавательной деятельности учащихся на уроке: индивидуальная (самостоятельная работа учащихся), фронтальная и групповая. Каждая форма имеет свои недостатки и преимущества, поэтому, планируя урок, учитель должен подбирать сочетание форм так, чтобы усилить сильные и нейтрализовать слабые стороны каждой формы.

ГЛАВА II. АНАЛИЗ ОПЫТНО- ЭКСПЕРИМЕНТАЛЬНОЙ РАБОТЫ ПО ПРИМЕНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ УЧАЩИХСЯ И ДРУГИХ ФОРМ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ НА ФАКУЛЬТАТИВНЫХ ЗАНЯТИЯХ В ВЫПУСКНЫХ КЛАССАХ.

Выводы по 2 главе.

Во 2 главе давался анализ опытно- экспериментальной работе, проведённой на факультативных занятиях в выпускных классах средней школы №9 г. Куйбышева НСО. Первым этапом этой работы было выявление учебных возможностей учеников. В данной главе рассказано о том, как были построены занятия на факультативе. Во второй главе приводятся результаты опытно-экспериментальной работы, которые подтверждают выдвинутую нами рабочую гипотезу о том, что самостоятельная работа учащихся является одной из эффективнейших форм обучения, способствует лучшему усвоению знаний, развитию навыков и умений по применению этих знаний, повышает уровень активности учащихся.

Противоречие.

Итак, получаем: левая положительная часть меньше отрицательной правой, что не имеет смысла.

Решим неравенство

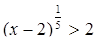
Возведем обе части неравенства в пятую степень, получим x – 2 > 32, откуда x > 34.

Ответ: x > 34.

Классические неравенства.

Рассмотрим некоторые наиболее важные для математического анализа неравенства. Эти неравенства служат аппаратом, который повседневно используют специалисты, работающие в этой области математики.

Теорема о среднем арифметическом и среднем геометрическом.

Теорема 1. Среднее арифметическое любых двух неотрицательных чисел а и b не меньше их среднего геометрического, т. е.:

(1)

Равенство имеет место в том и только том случае, когда a = b.

Доказательство. Поскольку квадратный корень может доставить немало хлопот, мы постараемся от него избавиться, положив a = c², b = d², что допустимо, ибо в теореме 1 предполагается, что числа а и b неотрицательны. При этом соотношение (1), в справедливости которого для произвольных неотрицательных чисел а и b мы хотим убедиться, примет следующий вид:

, (2)

где с и d – произвольные действительные числа.

Неравенство (2) имеет место в том и только том случае, когда

что в силу основных правил, относящихся к неравенствам, равносильно тому, что

с² + d² – 2cd ≥ 0 (3)

Но с² + d² – 2cd = (с – d)² , значит неравенство (3) равносильно

(с – d)² ≥ 0 (4)

Так как квадрат любого действительного числа неотрицателен, то ясно, что соотношение (4) всегда имеет место. Значит справедливы и неравенства (3), (2), (1). Равенство в формуле (4), а значит и в формуле (1) достигается в том и только в том случае, когда c – d = 0, т.е. c = d, или, иначе говоря, когда a = b.

Покажем теперь, что теорему 1 можно вывести геометрическим путем простого сравнения некоторых площадей.

Рассмотрим график функции у = х, изображенный на рисунке.

Пусть S и Т точки прямой у = х с координатами (с, с) и (d, d). Рассмотрим также точки Р(с, 0), Q(0, d), R(c, d). Так как длина отрезка ОР равна с, то длина отрезка PS также равна с. Поэтому площадь ∆OPS, полупроизведение длин его основания и высоты равна .

Рассмотрим теперь прямоугольник OPRQ. Он полностью покрывается ∆OPS и ∆OQT, так что

S_OPS + S_OQT ≥ S_OPRQ (5)

Так как площадь прямоугольника OPRQ – произведение длин его основания и высоты – равна сd, то при помощи алгебраических символов соотношение (5) можно записать так:

Кроме того, легко видеть, что равенство достигается только тогда, когда площадь ∆TRS равна нулю, что возможно только при условии совпадания точек S и Т, т. е. когда с = d.

Теорема 2. Среднее арифметическое любых трех неотрицательных чисел a, b и с не меньше их среднего геометрического, т.е.

(1)

Равенство достигается в том случае и только том случае, когда а = b = с.

Доказательство: пусть а = х³, b = у³, с = z³.

Подставим эти значения в неравенство (1):

, (2)

что равносильно неравенству

x³ + y³ + z³ – 3xyz ³ 0 (3)

Мы докажем теорему 2, если установим, что неравенство (3) имеет место для произвольных неотрицательных чисел x, y, z.

x³ + y² + z² – 3xyz = (x + y + z + )(x² + y² + z² – xy – xz – yz) (4)

x + y + z – неотрицательное число, покажем, что

x² + y² + z² – xy – xz – yz ³ 0 (5)

Выпишем три неравенства x² + y² ³ 2xy, x² + z² ³ 2xz, y² + z² ³ 2yz (эти неравенства истинны по теореме 1) и сложим их почленно:

2(x² + y² + z²) ³ 2(xy + xz + yz)

это неравенство равносильно неравенству (5). Равенство достигается тогда и только тогда, когда x = y = z.

Мы получили, что в (4) левая часть ³ 0, т.е. неравенство (3) имеет место. Но неравенство (3) равносильно (1). Теорема доказана. Условие x = y = z равносильно условию a = b = c.

Теорема будет верна и для n чисел, примем ее без доказательства.

Теорема 3. Среднее арифметическое любых n неотрицательных чисел а₁, а₂,…а_n не меньше их среднего геометрического, т.е.

Равенство достигается в том и только том случае, когда а1 = а2 = аn.

Неравенство Коши.

а) Двумерный вариант:

(1)

для любых неотрицательных чисел a, b c, d.

Доказательство. Так как a, b, c, d – неотрицательные, то ac + bd ³ 0 и имеем право возвести в квадрат обе части неравенства (1):

(a² + b²)(c² + d²) ³ (ac + bd)² (2)

В первую очередь отметим, что неравенство a² + b² ³ 2ab, на котором основывались все выводы в предыдущих теоремах, является простым следствием тождества a² – 2ab + b² = (a – b)², верного для всех действительных чисел. Рассмотрим произведение

(a² + b²)(c² + d²)

Произведя умножение, получим многочлен a²c² + b²d² + a²d² + b²c²,

Совпадающий с тем, который получается после раскрытия скобок в выражении (ac + bd)² + (bc – ad)²

Отсюда получаем

(a² + b²)(c² + d²) = (ac + bd)² + (bc – ad)² (3)

Так как квадрат (bc – ad)² неотрицателен, то из (3) следует неравенство

(a² + b²)(c² + d²) ³ (ac + bd)²

для любых действительных чисел a, b, c, d.

Мы получили неравенство (2) – неравенство Коши для любых действительных чисел a, b, c, d.

Для любых неотрицательных чисел a, b, c, d неравенство Коши примет вид (1). Из соотношения (3) вытекает, что равенство в (2), а значит и в (1) достигается тогда и только тогда, когда

bc – ad = 0 (4)

В этом случае говорят, что две пары чисел (a, b) и (c, d) пропорциональны. При с ¹ 0 и d ¹ 0 условие (4) можно записать следующим образом:

Геометрическая интерпретация.

Рассмотрим треугольник, изображенный на рисунке.

Очевидно, что длины отрезков OР и OQ и PQ определяются равенствами

ОР = (a² + b²)^½

ОQ = (c² + d²)^½

РQ = [(a – c)² + (b – d)²]^½

Обозначим угол между сторонами ОР и OQ через q. На основании теоремы косинусов имеем:

PQ2 = OP2 + OQ2 – 2OP × OQ cosq

Подставляя значения OP, OQ, и РQ и упрощая полученное выражение, имеем

Поскольку значение косинуса всегда заключено между –1 и +1, мы имеем

-1 £ cos q £ 1

или

значит

А это двумерный вариант неравенства Коши. Кроме того, мы видим, что равенство здесь достигается тогда и только тогда, когда сos q =1, т.е. когда q = 0 или q = p, - другими словами в том и лишь в том случае, когда точки О, Р, и Q лежат на одной прямой. При этом должно иметь место равенство подъемов прямых ОР и OQ; иначе говоря, если с ¹ 0 и d ¹ 0, то должно быть

б) Трехмерный вариант неравенства Коши.

Вышеприведенная интерпретация неравенства Коши для двумерного случая хороша еще и тем, что позволяет нам при помощи геометрической интуиции легко сообразить, какой вид будут иметь аналогичные результаты, относящиеся к более сложному случаю любого числа измерений. Перейдем к случаю трехмерного пространства. Пусть Р(а₁, а₂, а₃) и Q(b₁, b₂, b₃) – две точки, не совпадающие с началом координат О (0, 0, 0). Тогда косинус угла q между прямыми ОР и OQ будет определяться равенством

которое, в силу того, что сosq £ 1, приводит к трехмерному варианту неравенства Коши для неотрицательных чисел а_i и b_i, i = 1, 2, 3

(1)

Равенство здесь достигается тогда и только тогда, когда три точки О, Р и Q лежат на одной прямой, что выражается соотношениями

имеющими смысл при условии, что все числа bi, стоящии в знаменателях отличны от нуля.

Чисто алгебраическое доказательство трехмерного варианта неравенства Коши (1) можно вывести из следующего тождества:

(a₁² + a₂² + a₃²)(b₁² + b₂² + b₃²) – (a₁b₁ + a₂b₂ + a₃b₃)² = (a₁²b₂² + a₂²b₁²) +

+ (a₁²b₃² + a₃²b₁²) + (a₂²b₃² + a₃²b₂²) – 2a₁b₁a₂b₂ – 2a₁b₁a₃b₃ – 2a₂b₂a₃b₃ =

= (a₁b₂ – a₂b₁)² + (a₁b₃ – a₃b₁)² + (a₂b₃ – a₃b₂)² (2)

Очевидно, что последнее выражение в (2) неотрицательно, так как оно состоит из суммы трех неотрицательных членов. Поэтому

(a₁² + a₂² + a₃²)(b₁² + b₂² + b₃²) – (a₁b₁ + a₂b₂ + a₃b₃)²³ 0.

Приведем еще одно доказательство этого неравенства, которое пригодится нам дальше.

Начнем с основного неравенства (х – у²) ³ 0, которое можно записать в следующем виде:

(3)

Неравенство (3) имеет место для любых действительных чисел х и у. Вместо х и у последовательно подставим в (3) следующие выражения:

сначала:

затем

и, наконец,

где a_i, b_i – действительные числа.

Складывая три полученных таким образом неравенства, имеем

что бесспорно равносильно неравенству

(a₁² + a₂² + a₃²)^½(b₁² + b₂² + b₃²)^½ ³ a₁b₁ + a₂b₂ + a₃b₃

А это неравенство равносильно неравенству (1) при a_i, b_i – неотрицательных.

в) n – мерный вариант неравенства Коши будет выглядеть так

где a_i, b_i, i = 1, 2, … n – неотрицательные числа.

Неравенство Гёльдера.

Одно из наиболее полезных неравенств математического анализа – неравенство Гёльдера. Оно утверждает, что для любой системы неотрицательных чисел a_i и b_i (i – 1, 2, … , n)

(1)

где числа р и q удовлетворяют условию

и р > 1

Фактически мы докажем неравенство (1) только для рациональных р и q. Однако окончательный результат сохраняет силу и для иррациональных р и q.

Начнем с неравенства

(2)

Оно выводится как частный случай теоремы о среднем арифметическом среднем геометрическом. Положим, что первые m чисел x_i в неравенстве

равны некоторому неотрицательному числу х, тогда остается N-m чисел и пусть они равны неотрицательному числу у, т.е.

x₁ = x₂ = … = x_m = x

x_m+1 = x_m+2 = … = x_n= y

В этом случае теорема о среднем арифметическом и среднем геометрическом для чисел x₁, x₂, … , x_n примет вид

или

Здесь n – любое целое число, а m – целое число значения которого заключены в пределах 1 £ m £ n – 1. Отсюда следует, что число m/n может быть любой рациональной дробью r, принадлежащей интервалу 0 < r < 1. Теперь последнее неравенство можно переписать так:

rx + (1 – r)y ³ x^ry^1-r (3)

Это неравенство имеет место для любых неотрицательных чисел х и у и для любой дроби r, значения которой заключены между 0 и 1. Равенство здесь достигается тогда и только тогда, когда х = у.

Обозначим число r через 1/р; поскольку 0 < r < 1, то p > 1. Отсюда

. Пусть , тогда и

В этих обозначениях неравенство (3) принимает вид

(4)

С целью исключить из рассмотрения дробные показатели степени положим

х = а^р, у = b^р.

При этом неравенство (4) принимает вид

, где a и b – неотрицательные числа, а р и q – такие рациональные числа, что . Равенство здесь достигается тогда и только тогда, когда а^р = b^р. Итак, мы вывели неравенство (2).

Положим

затем

и т. д. (как в доказательстве неравенство Коши) и сложим неравенства, получающиеся после последовательных подстановок этих значений в (2). При этом получим

(5)

Используя равенство , получаем неравенство, равносильное (1). Равенство в (5) достигается тогда и только тогда, когда все отношения b_i/a_i равны между собой.

Неравенство треугольника.

Из геометрии мы знаем, что сумма длин двух сторон треугольника не меньше длины его третьей стороны. Посмотрим, как можно выразить эту теорему алгебраически.

Рассмотрим треугольник ORP, расположенный так, как показано на рисунке.

Геометрическое неравенство ОР + PR ³ OR равносильно алгебраическому неравенству треугольника

(1)

Для доказательства возведем обе части неравенства (1) в квадрат, при этом мы придем к неравенству, равносильному (1):

Легко видеть, что последнее неравенство в свою очередь равносильно неравенству:

Но это неравенство является простым следствием неравенства Коши

что и доказывает неравенство треугольника.

Равенство в неравенстве треугольника, как и в неравенстве Коши достигается тогда и только тогда, когда х₁ = кх₂ и у₁ = ку₂, где к – неотрицательный коэффициент пропорциональности.

Доказательство неравенства треугольника можно обобщить, следуя по тому же пути, что и при выводе неравенства Гёльдера, а именно доказать, что неравенство

имеет место для любых действительных значений x_i, y_i. Равенство достигается в том и только том случае, когда числа x_i и y_i пропорциональны и коэффициент пропорциональности положителен.

Рассмотрим еще одно доказательство неравенства треугольника, которое можно использовать также и для получения более общих результатов. Имеет место тождество

(х₁ + х₂)² + (у₁ + у₂)² = х₁(х₁ + х₂) + у₁(у₁ + у₂) + х₂(х₁ + х₂) + у₂(у₁ + у₂)

Неравенство Коши в форме, использующей квадратные корни, применим по очереди к двум выражениям:

х₁(х₁ + х₂) + у₁(у₁ + у₂) и

х₂(х₁ + х₂) + у₂(у₁ + у₂).

Мы получим

(х₁² + у₁²)^1/2 [(х₁ + х₂)² + (у₁ + у₂)²]^1/2 ³ х₁(х₁ + х₂) + у₁(у₁ + у₂) и

(х₂² + у₂²)^1/2 [(х₁ + х₂)² + (у₁ + у₂)²]^1/2 ³ х₂(х₁ + х₂) + у₂(у₁ + у₂)

Сложим эти два неравенства

[(х₁² + у₁²)^1/2 + (х₂² + у₂²)^1/2]*[(х₁ + х₂)² + (y₁ + у₂)²]^1/2³ (х₁ + х₂)² + (у₁ + у₂)²

разделив обе части на общий множитель

[(х₁ + х₂)² + (у₁ + у₂)²]^1/2 ,

будем иметь

(х₁² + у₁²)^1/2 + (х₂² + у₂²)^1/2 ³ [(х₁ + х₂)² + (у₁ + у₂)²]^1/2

таким образом, мы еще раз доказали неравенство треугольника. Равенство опять будет иметь место тогда и только тогда, когда х₁ = кх₂ и у₁ = ку₂, где к – неотрицательный коэффициент пропорциональности, другими словами, тогда и только тогда, когда три точки О, Р и Q лежат на одной прямой, причем точки Р и Q расположены по одну сторону от точки О.

Неравенство Минковского.

Неравенство Минковского утверждает, что для любых неотрицательных чисел х₁, у₁, х₂, у₂ при любом р > 1

(х₁^р + у₁^р)^1/р + (х₂^р + у₂^р)^1/р ³ [(х₁ + х₂)^р + (у₁ + у₂)^р]^1/р (1)

Неравенство треугольника составляет частный случай неравенства Минковского для р = 2 и их доказательства подобны.

Запишем тождество

(х₁ + х₂)^р + (у₁ + у₂)^р = [х₁(х₁ + х₂)^р-1 + у₁(у₁ + у₂)^р-1] ×

× [х₂(х₁ + х₂)^р-1 + у₂(у₁ + у₂)^р-1]

и применим неравенство Гёльдера к каждому члену правой части этого тождества. В результате получим:

(х₁^р + у₁^р)^1/р= [ (х₁ + х₂)^(р-1)^q + (у₁ + у₂)⁽^р-1^)q]^1/q ³ х₁(х₁ + х₂)^р-1 + у₁(у₁ + у₂)^р-1

^и

(х₂^р + у₂^р)^1/р= [ (х₁ + х₂)^(р-1)^q + (у₁ + у₂)⁽^р-1^)q]^1/q ³ х₂(х₁ + х₂)^р-1 + у₂(у₁ + у₂)^р-1

Так как , то (p – 1)q = p. Складывая последние два неравенства, имеем

[(х₁ + х₂)^р + (у₁ + у₂)^р]^1/q[(х₁^р + у₁^р)^1/р + (х₂^р + у₂^р)^1/р] ³ (х₁ + х₂)^р + (у₁ + у₂)^р

Разделив затем на [(х₁ + х₂)^р + (у₁ + у₂)^р]^1/q

получим

(х₂^р + у₂^р)^1/р + (х₁^р + у₁^р)^1/р ³ [(х₁ + х₂)^р + (у₁ + у₂)^р]^1-1/q

Так как , то последнее неравенство полностью совпадает с требуемым неравенством Минковского (1).

Знак равенства в неравенстве (1) имеет место тогда и только тогда, когда точки (х₁ у₁) и (х₂ у₂) лежат на одной прямой с точкой (0, 0).

Аналогично обобщением неравенства Гёльдера и неравенства треугольника можно получить и неравенство Минковского для двух систем их n неотрицательных чисел х₁, х₂, … , х_n и у₁, у₂, … , у_n. Оно имеет вид:

[х₁^р + х₂^р +… х_n^р ]^1/р + [у₁^р + у₂^р+… + у_n^р]^1/р ³

³ [(х₁ + у₁)^р + (х₂ + у₂)^р + … +(х_n + у_n)^р]^1/р , где р ³ 1

При p < 1 знак неравенства следует изменить на обратный.

ЗАКЛЮЧЕНИЕ.

В дипломной работе изучен и дан анализ самостоятельной работе учащихся наряду с другими формами организации познавательной деятельности. На основе изученной психолого-педагогической литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения.

Разработано и проведено 8 занятий по теме «Иррациональные неравенства». На основе изученной литературы дается анализ иррациональных неравенств и способов их решения.

Проведение опытно- экспериментальной работы подтверждает выдвинутую гипотезу. Применение самостоятельной работы учащихся способствует лучшему усвоению знаний, о чем свидетельствуют результаты контрольной работы, способствует повышению активности познавательной деятельности учащихся. Конечно, если бы эксперимент длился дольше, то результаты были бы более ощутимы.

ЛИТЕРАТУРА.

1. Андреева И.Н. Индивидуальные творческие работы учащихся в обучении // Автореферат, МГПИ- М; 1967

2. Аношнин А.П. Оптимизация форм организации учебной деятельности школьников на уроке. // Автореферат, ЧГУ- Челябинск: 1986

3. Бабанский Ю.К. Оптимизация процесса обучения // Советская педагогика- М.: Просвещение

4. Верцинская Н.Н. Индивидуальная работа с учащимися- Минск: 1983

5. Дьяченко В.К. Организационные формы обучения и их развитие. //Советская педагогика- М: Просвещение, 1985, № 9

6. Дьяченко В.К. Организационная структура учебного процесса и ее развитие- М: Педагогика, 1989

7. Зотов Ю.Б. Организация современного урока.- М: Просвещение, 1984

8. Лийметс Х.И. Групповая работа на уроке. – М: Просвещение, 1975

9. Махмутов М.И. Вопросы организации процесса проблемного обучения. – Казань: Издательство Казанского университета, 1972

10. Николаева Т.М. Сочетание общеклассной, групповой и индивидуальной работы учащихся на уроке как одно из средств повышения эффективности учебного процесса. //Автореферат, М: 1972

11. Семенов Н.А. О способах организации обучения. //Советская педагогика, 1966, № 11

12. Стрезикозин В.П. Организация процесса обучения в школе. //М: Просвещение, 1968

13. Уфимцева М.А. Формы организации обучения в современной общеобразовательной школе. //М: Просвещение, 1986

14. Хабиб О.А. Организация учебно-познавательной деятельности учащихся. –М: Педагогика, 1979

15. Чередов И.М. Методика планирования школьных форм организации обучения. –Омск: Педагогика, 1983

16. Чередов И.М. Пути реализации принципа оптимального сочетания форм организации учебной деятельности в 5-9 классах. //Автореферат, КГУ, Красноярск, 1970

17. Чередов И.М. Система форм организации в советской общеобразовательной школе. –М: Педагогика, 1987

18. Чередов И.М. Формы учебной работы в средней школе. – М: Просвещение, 1988

19. Ю.В. Нестеренко и др. Задачи вступительных экзаменов по математике //М: Наука, 1980

20. Белоносов В.С. Задачи вступительных экзаменов по математике в НГУ //Новосибирск, НГУ, 1992

21. Литвиненко В.Н., Морднович А.Г. Практикум по элементарной математике. //М: Просвещение, 1991

22. Литвиненко В.Н. Морднович А.Г. Практикум по решению математических задач. //М: Просвещение, 1984

23. Вересова Е.Е. и др. Практикум по решению математических задач. //М: Просвещение, 1979

24. Блох А.Ш., Трухан Т.Л. Неравенства //Минск: Народная Асвета, 1972

25. Задачи повышенной трудности по алгебре и началам анализа //М: Просвещение, 1990

26. Коровкин П.П. Неравенства //М: Наука, 1974

27. Башмаков М.И. Уравнения и неравенства //М: Наука, 1976

28. Беккенбах Э., Беллман Р. Введение в неравенства //М: Мир, 1965

29. Невежский Г.Л. Неравенства //М: Учпедгиз, 1947

30. Алгебра, 8 класс //М: Просвещение, 1980

ПРИЛОЖЕНИЕ.

Введение

Изучая школьную программу, я выяснила, что иррациональные неравенства не рассматриваются в курсе средней школы. В 11классе изучаются лишь иррациональные уравнения. Они входят в раздел «Показательные функции», и учитель может уделить им внимание в течение 2-3 уроков. Однако для тех учащихся, которые хотят иметь хорошую подготовку для поступления в ВУЗы этого явно недостаточно. Просматривая программы, предлагавшиеся на вступительных экзаменах в НГУ и МГУ находим, что кроме иррациональных уравнений в них предлагается решить и иррациональные неравенства. Например, НГУ:

75 год механико-математический факультет

В-I решить неравенство

В-II решить неравенство

81 год геолого – геодезический факультет

В-I решить неравенство

В-IV решить неравенство

81 год физический факультет

В – I решить неравенство

В – II решить неравенство

МГУ:

78 год механико – математический факультет

В-I решить неравенство

79 год физический факультет

В-I решить неравенство

78 год химический факультет

В-I решить неравенство

Цели проведения и написания этого факультатива: подготовить учащихся к поступлению в ВУЗы, расширить и систематизировать полученные ранее сведения и решении иррациональных уравнений, научить учащихся решать иррациональные неравенства, а также отработать технические навыки тождественных преобразований иррациональных уравнений. Данный материал требует достаточной логической грамотности учащихся, так как для того, чтобы найти множество решений иррационального неравенства, приходится, как правило, возводить обе части неравенства в натуральную степень. Необходимо довести до понимания учащихся, что несмотря на внешнюю схожесть процедуры решения иррационального уравнения и иррационального неравенства, между ними существует большое отличие. При решении неравенства невозможно проверкой установить «лишние» решения, которые могут появиться при возведении в четную степень. Единственный способ, гарантирующий правильность ответа, заключается в том, что мы должны следить за тем, чтобы при каждом преобразовании неравенства у нас получалось неравенство, эквивалентное исходному. Цель дипломной работы – оказать конкретную помощь учителю в подготовке учеников к поступлению в ВУЗы, в более углубленном изучении материала. Самым распространенным методом обучения решению иррациональных неравенств является выявление типичных способов решения иррациональных неравенств. Наша задача – дать основные рекомендации для поиска решения неравенств и приобрести некоторый опыт при решении.

Занятие№1

Тема: Понятие иррационального неравенства, его особенности.

Цель: дать понятие об иррациональных неравенствах, научить находить ОДЗ иррациональных неравенств.

I. Вспомнить (вопросы классу):

1) что называется корнем n – ной степени из числа а?

2) Что называется арифметическим корнем n – ной степени из числа а (а ³ 0)?

3) Какие свойства арифметического корня n – ной степени вы знаете?

II. Самостоятельная работа на 2 варианта

В – I В – II

1) Докажите, что истинно равенство

2) Найдите значений корня

3) Найдите значение выражения

4) Решите уравнения

х³ = 4 х⁴ = 10

х⁴ = -10 х³ = -4

х⁶ = 7 х⁵ = 6

5) Решите уравнение и неравенства

6) Найти значения выражения

III. Учитель объясняет новый материал, опираясь не знания учащихся.

IV. Найти ОДЗ неравенств (учащиеся решают самостоятельно, затем устно проверяем ответы)

V. Д/з

1 группа самостоятельно разбирает тему «Простейшие иррациональные неравенства, содержащие радикал четной степени» и пишет доклады по этой теме по плану:

1) Уединение радикала

2) Решение неравенств вида

3) Решение неравенств вида

4) Примеры

2 группа повторяет пройденный материал.

Занятие №2

Тема: Простейшие иррациональные неравенства, содержащие переменную под знаком радикала четной степени.

Цель: Отработать навыки решения иррациональных неравенств, содержащих переменную под знаком радикала четной степени.

I. Чтение доклада одним из учащихся 1 группы, дополнения остальных учащихся 1 группы, разбор у доски 3 – 4 примеров, которые ребята нашли и решили дома.

II. Следующие неравенства ребята решают самостоятельно, затем в парах проверяют решения друг у друга.

Ответ: х ³

Ответ: х £ -1 и х ³ 1

Ответ: х ³

Ответ:

III. Д/з

1 группа самостоятельно разбирает простейшие иррациональные неравенства, содержащие переменную под знаком радикала нечетной степени и пишет доклад по плану:

1) возведение неравенств в нечетную степень;

2) примеры с решениями.

2 группа учит решение иррациональных неравенств, разобранных в классе, решает неравенства:

Занятие №3

Тема: Решение иррациональных неравенств, содержащих переменную под знаком радикала нечетной степени.

Цель: Закрепление изученного, научить учащихся решать простейшие иррациональные неравенства, содержащие переменную под знаком радикала нечетной степени.

I. Повторение

1) Расскажите правила решения неравенств вида

а)

б)

в)

г)

2) Решить неравенства (кто-то из учащихся 2 группы решает у доски, остальные – в тетрадях)

а)

Ответ:

б)

Ответ:

II. Разбор нового материала (ребята из 1 группы рассказывают, объясняют свои примеры).

III. Самостоятельно решить неравенства

x(x-3)(x+2)>0

-2 0 3

Ответ:

- + - +

Ответ:

Ответы проверить в парах.

IV. Подведение итогов занятия: видим, что при возведение неравенств в нечетную степень эквивалентность не нарушается и под знаком радикала выражение может принимать любые значения. А в четную степень имеем право возводить только те неравенства, у которых обе части неотрицательны; под знаком радикала четной степени может стоять только неотрицательная функция.

V. Д/з

1 группа изучает тему «Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени», подбирает и решает неравенства по теме. Цель этой самостоятельной работы: научиться самим и научить затем ребят из второй группы решать такие неравенства.

2 группа повторяет изученное.

Занятие №4.

Тема: Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени.

Цель: отработка навыков решения иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени.

I. Учащиеся из 1 группы у доски рассказывают новый материал, объясняют неравенства, которые они решили дома, с помощью учителя разбираются непонятные места.

II. Делаем вывод: при возведении таких неравенств в четную степень эквивалентность не нарушается только тогда, когда обе части неравенства неотрицательны. Некоторые неравенства следует сначала привести к такому виду, когда ясно видно, что обе части его неотрицательны.

Решим пример (кто-то из ребят 2 группы решает у доски).

Ответ:

III. Решить неравенства

Ответ:

На ОДЗ

Значит неравенство истинно.

Ответ:

IV. Д/з

1 группа пишет доклады по теме: «Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечетной степени». Особое внимание обратить на решение неравенств вида:

и неравенств, содержащих радикалы третьей и второй степени.

2 группа: повторение, решить неравенства а) ;

б)

Занятие №5

Тема: решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечетной степени.

Цель: познакомить учащихся с неравенствами, содержащими переменную под знаком двух и более радикалов нечетной степени и показать способы их решения.

I. Проверка Д/з 2 группы (устно)

II. Учащиеся 1 группы читают доклады, объясняют у доски решенные неравенства. Все остальные ребята с учителем разбирают решения.

III. Решить неравенства (решения проверить друг у друга в парах).

Ответ:

+ - +

-1 3

Ответ:

найдем решение соответствующего уравнения:

возводим в куб

делаем замену

Проверка:

-2=1 – ложно, корень х = 0 – посторонний

Ответ:

решим соответствующее уравнение:

возводим в куб

делаем подстановку

Проверка:

1 3

Ответ:

возводим в куб

При

Значит последнее неравенство на ОДЗ всегда истинно.

Ответ:

IV. Д/з

1 группа на примерах рассматривает решение иррациональных неравенств с параметрами.

2 группа учит рассмотренный в классе материал, решает неравенства

а)

б)

Занятие №6

Тема: Решение иррациональных неравенств с параметрами.

Цель: научить учащихся решать иррациональные неравенства с параметрами.

I. Вопросы классу

1) Что называют параметрами?

2) Когда неравенство, содержащее параметры считается решенным?

II. Учащиеся из 1 группы рассказывают о решении неравенств, которые они решали дома. Учитель помогает сделать выводы.

III. Решить неравенства

все значения принадлежат ОДЗ, так как значит

Ответ: 1)

ОДЗ неравенства

а) при а < 0

на ОДЗ всегда и неравенство истинно

б) при

последнее неравенство имеет смысл при , значит при нет решений

при

возводим в квадрат обе части неравенства

1 – 2а² + a⁴ > 4a²(x – 1)

a⁴ + 2a² + 1 > 4a²x

(a² + 1)² > 4a²x

Ответ: 1) при

2) при нет решений

3) при

ОДЗ неравенства

а) при а = 0 нет решения

б) при а > 0 ОДЗ

х = 0 и х = а не удовлетворяют неравенству х(х – а) < 0 на ОДЗ, а

всегда и неравенство истинно всегда

в) при а < 0 ОДЗ х Î [a;0] неравенство истинно

Ответ: а) если а > 0 0 < x < a

б) если а = 0 нет решения

в) если а < 0

при а £ 0 неравенство не имеет смысла, так как получаем

при а > 0

Сравним а² и :

Ответ: если a > 2, то

если a ³ 2, Æ

ОДЗ неравенства:

а) при а = 0 ОДЗ х £ 0

при х = 0 решения нет

при х < 0 - истинно

б) при а < 0

2а а

ОДЗ х £ 2а

последнее неравенство истинно на ОДЗ, кроме х = 2а

в) при а > 0

ОДЗ х £ а

(а – х)(2а – х) > 0

истинно на ОДЗ, кроме х = а

Ответ: а) при а = 0 х < 0

б) при a < 0 x < 2a

в) при а > 0 x < a

IV. Д/з

1 группа подбирает и решает неравенства по теме «Решение иррациональных неравенств» способом введения новой переменной».

2 группа решает неравенства

а)

б)

Занятие №7

Тема: Решение иррациональных неравенств, способом введения новой переменной.

Цель: познакомить учащихся с методом решения иррациональных неравенств – введением новой переменной.

I. Разбор неравенств, приготовленных учащимися 1 группы.

II. Решить неравенства

тогда х² + 5х + 4 = у² – 24

у² – 5у – 24 < 0

у² – 5у – 24 = 0

D = 25 + 96 = 121

у₁ = -3 у₂ = 8

(у – 8)(у + 3) < 0

-3 < y < 8

- истинно для любого х из ОДЗ: х² + 5х + 28 ³ 0 – истинно всегда (D < 0, a > 0)

Ответ: х Î]–9; 4[

- истинно для любого х из ОДЗ х² – 3х + 5 ³ 0 – истинно всегда

D <0, a = 1 > 0

Ответ: х Î [-1; 4]

ОДЗ: 5 – х ³ 0 или х £ 5

пусть , тогда у > x – 3, у ³ 0

выразим х через у: у² = 5 – х Þ х = 5 – у²

получаем систему:

Значения х < 4 принадлежат ОДЗ

Ответ: х < 4

ОДЗ: 2х + 10 ³ 0, х ³ -5 3x – 5 ³ 0, x ³

пусть , тогда у < 3x – 5, y ³ 0

выразим х через у : у² = 2х + 10 Þ х = ½у² – 5

получаем систему:

x > 3

Значения х > 3 принадлежат ОДЗ

Ответ: х > 3

Найдем ОДЗ неравенства:

х ³ 2

при х ³ 2 второе и третье неравенства системы истинны

ОДЗ: х ³ 2

пусть

|t + 1| - |t – 1| > 1

a) t £ -1

-t – 1 + t – 1 > 1

-2 > 1 – ложно Æ

б) –1 < t £ 1

t + 1 + t –1 >1

учитывая, что –1 < t £ 1, получаем

в) t > 1

t + 1 – t + 1 > 1 2 > 1 – истинно

решением неравенства на всех трех промежутках будет

x > 2,25 – принадлежит ОДЗ

Ответ: x > 2,25

ОДЗ неравенства:

пусть , тогда

|t +-3| + |t – 2| > 1

a) t £ 2

- t + 3 – t + 2 > 1 t <2

учитывая, что t £ 2 получаем t <2

б) 2 < t £ 3

- t + 3 + t – 2 > 1 1 > 1 – ложно Æ

в) t > 3

t – 3 + t – 2 > 1 t >3

получаем:

учитывая ОДЗ получаем: 2 £ x < 6, x > 11

Ответ: 2 £ x < 6, x > 11

III. Д/з

1 группа разбирает способы решения иррациональных неравенств домножением обеих частей на некоторое число или выражение, разложением подкоренного выражения на множители, выделением полного квадрата в подкоренных выражениях.

2 группа решает неравенства:

а)

б)

Занятие № 8

Тема: Решение иррациональных неравенств, способами домножения обеих частей на некоторое число, либо выражение, выделения полного квадрата в подкоренных выражениях, либо разложения подкоренного выражения на множители.

Цель: дать учащимся представление о способах решения иррациональных неравенств.

I. Разбор Д/з 2 группы (устно)

II. Разбор задач, приготовленных 1 группой.

III. решить неравенства

ОДЗ: х ³ 1

домножим на

последнее неравенство всегда истинно на ОДЗ

Ответ: х ³ 1

ОДЗ: х < 2

домножим на

Ответ:

Ответ: хÎ[0;3]

ОДЗ: х £ 1, х £ 5, х = 2

учитывая ОДЗ получаем

Ответ:

Итоговая контрольная работа

Вариант I.

Решить неравенства

Вариант II.

Решить неравенства

Филиппова Ольга Владимировна.

Дипломная работа «Организация познавательной деятельности учащихся на факультативных занятиях по теме «Иррациональные неравенства»

Руководитель: Кузьмичев Анатолий Иванович.

З А Щ И Т А (устно)

Дипломная работа состоит из введения, трех глав, заключения, списка литературы и приложения с разработкой факультатива по теме.

В дипломной работе мне хотелось собрать и проанализировать знания, полученные за пять лет обучения, и применить их к конкретной задаче. А именно, я попыталась на примере изучения очень трудной и, прямо сказать, непопулярной среди школьников темы «Иррациональные неравенства» подтвердить положение о том, что интерес, а с ним и знания, умения, навыки приходят вместе с упорным трудом, причем, этот труд должен носить в большой мере самостоятельный характер и в части подготовки к занятиям, и даже части проведения и поиска нужных форм их организации.

Важным подспорьем в развитии познавательного интереса учащихся являются, как оказалось, исторические сведения по теме. Их поиск значительно активизировал работу с литературой, в которой помимо всего учащиеся искали еще и сведения по методике проведения занятий, изучения темы, задач, предлагавшихся на вступительных экзаменах в различные ВУЗы.

При проведении факультативных занятий ученики были разбиты на 2 группы: экспериментальную и контрольную, примерно равные по силам. У всех учащихся была одна цель – подготовиться к вступительным экзаменам в ВУЗ. Это определило их первоначальный интерес. Разбиение на 2 группы проводилось по желанию самих ребят. Они посещали одни и те же занятия, изучали на уроках один и тот же материал. Но ребята 1-ой экспериментальной группы имели гораздо больше возможностей и причин для самостоятельной работы по теме: они в качестве домашнего задания должны были самостоятельно изучить новую тему, начиная с поиска материала (под руководством учителя), далее написать доклады, найти и прорешать задачи, а затем рассказать все это остальным участникам факультатива.

Учитель предлагал темы, литературу, определял докладчиков, акцентировал в нужных местах внимание и на уроках давал задачи по теме, которые, по его мнению, нужно было прорешать, а докладчики таковых не предложили.

Заключительная работа по теме показала, что учащиеся из 1-ой группы получили результаты, пусть и ненамного, но лучше учащихся контрольной группы.

Но, кроме того, они получили бесценный опыт самостоятельной работы, который, как мне кажется, еще даст свои положительные результаты в будущем.

По материалам проведенного факультатива и был написан диплом.

В первой главе разбираются основные формы организации познавательной деятельности, проводится их сравнительный анализ и выясняются оптимальные сочетания и взаимодействия этих форм (в зависимости от специфики материала и от того, как он усвоен учащимися, выбирались сочетания фронтальной, групповой и индивидуальной форм).

Во второй главе рассматриваются вопросы методики организации факультативных занятий, необходимость и обоснованность их проведения. Далее излагаются результаты опытно-экспериментальной работы.

Глава три – основная часть работы. В ней содержится необходимый теоретический и практический материал для факультатива. К сожалению, сюда не вошли все задачи, которые предлагали учащиеся, найденные ими к занятиям, из-за их однотипности с опубликованными.

Учащимися, с помощью учителя, были выделены 9 частных случаев и способов решения иррациональных неравенств и к каждому из них учащиеся придумывали неравенства для последующего решения их всем классом.

Учителем была поставлена задача выяснить, какие трудности характерны для каждого из способов решения.

Большое внимание уделялось оформлению решения задачи, в частности, записи ответа, за что в ВУЗах на приемных экзаменах часто снижают бал.

Эта часть диплома может служить основой для проведения соответствующего факультатива для любого учителя. Данная глава заканчивается подборкой задач по теме и доказательством классических неравенств.

В приложении приводится разработка факультатива из 8 занятий по теме «Иррациональные неравенства» и итоговая контрольная работа.

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

ДИПЛОМНАЯ РАБОТА

Организация познавательной деятельности учащихся

на факультативных занятиях по теме

«Иррациональные неравенства»

Выполнила: студентка

VI курса МФ

Филиппова Ольга

Владимировна

Научный руководитель:

Кузьмичев Анатолий

Иванович

старший преподаватель

Кафедры алгебры

Г.НОВОСИБИРСК

Г.

СОДЕРЖАНИЕ

Введение.

Глава 1. Организация познавательной деятельности на факультативных занятиях.

1. История развития форм обучения. Сущность понятия “форма” организации познавательной деятельности.

2. Самостоятельная работа учащихся - один из важнейших способов организации познавательной деятельности.

3. Фронтальная и групповая формы организации познавательной деятельности учащихся.

4. Оптимальное сочетание и взаимодействие форм учебно-познавательной деятельности.

Выводы по 1-й главе.

1. Изучение учебных возможностей учащихся. Методика организации факультативных занятий.

2. Результаты опытно-экспериментальной работы.

Выводы по 2-й главе.

Глава 3. Иррациональные неравенства, способы их решения.

1. Краткие исторические сведения.

2. Неравенства и их основные свойства.

3. Корень n-ой степени. Иррациональные неравенства.

4. Решение простейших иррациональных неравенств.

1-2

3-6

7-10

11-12

13-15

17-21

22-23

25-27

28-38

39-40

41-48

7. Решение иррациональных неравенств с параметрами.

8. Решение иррациональных неравенств, способом ведения новой переменной.

9. Способ домножения обеих частей иррационального неравенства на некоторое число, либо выражение.

11. Решение иррациональных неравенств путём проб, выводов.

12. Решение более сложных примеров.

13. Подборка задач по теме «Решение иррациональных неравенств».

14. Классические неравенства.

Заключение.

Литература.

Приложение.

1. Введение.

2. Разработка факультатива по теме «Иррациональные неравенства».

49-53

54-59

60-65

66-71

72-74

75-77

79-81

83-97

99-100

101-103

104-133

ВВЕДЕНИЕ.

В соответствии с целью и принятой гипотезой были выдвинуты следующие задачи:

1. Изучение психолого-педагогической литературы по данной теме.

2. Характеристика и анализ самостоятельной работы учащихся.

3. Изучение учебных возможностей учащихся на факультативе.

4. Проведение опытно-экспериментальной работы в выпускных классах средней школы № 9 г. Куйбышева НСО.

Выполнение задач осуществлялось следующими методами:

1. Анализ психолого-педагогической литературы;

2. Наблюдение;

3. Анкетирование учащихся;

4. Беседы с учащимися;

5. Проведение опытно-экспериментальной работы.

ГЛАВА I . ОРГАНИЗАЦИЯ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКАХ МАТЕМАТИКИ

Дата: 2019-07-24, просмотров: 176.

12 3 4 5 6 7 8 9 10 Следующая ⇒