Определение. Граф называется эйлеровым, если в нем существует цикл, проходящий по всем ребрам графа по одному разу.
Определение. Граф называется гамильтоновым, если в нем существует цикл, проходящий по всем вершинам по одному разу.
Эйлеровы графы изучены наиболее полно, получено необходимое и достаточное условие эйлеровости графа.
Теорема об эйлеровых графах. Cвязный граф будет эйлеровым тогда и только тогда, когда степень каждой вершины четная.
Доказательство. Пусть граф эйлеров, т. е. существует цикл, проходящий по всем ребрам графа по одному разу. Если в вершину 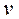 пришли по ребру
пришли по ребру  , то должно существовать ребро
, то должно существовать ребро  , по которому из этой вершины можно выйти. Если в эту же вершину
, по которому из этой вершины можно выйти. Если в эту же вершину 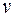 попали еще раз, то уже по ребру
попали еще раз, то уже по ребру  и выходим по ребру
и выходим по ребру  . Число ребер, по которым мы попадаем в некоторую вершину, равно числу ребер, по которым мы из нее выходим, следовательно,
. Число ребер, по которым мы попадаем в некоторую вершину, равно числу ребер, по которым мы из нее выходим, следовательно,  – четное число.
– четное число.
Пусть  – четное число для любой вершины
– четное число для любой вершины 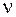 и граф связен. Покажем, что в этом случае существует цикл, проходящий по всем ребрам по одному разу. Возьмем вершину
и граф связен. Покажем, что в этом случае существует цикл, проходящий по всем ребрам по одному разу. Возьмем вершину  и пойдем из нее по ребрам и вершинам графа G так далеко, насколько это возможно. Ребра в этом пути не должны повторяться. Если мы пришли в вершину
и пойдем из нее по ребрам и вершинам графа G так далеко, насколько это возможно. Ребра в этом пути не должны повторяться. Если мы пришли в вершину 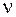 по некоторому ребру, то выйдем из нее по другому ребру, это возможно, так как
по некоторому ребру, то выйдем из нее по другому ребру, это возможно, так как  – четное число. Этот путь завершится в вершине
– четное число. Этот путь завершится в вершине  , так как только у нее осталось нечетное число неиспользованных ребер. Таким образом, мы получили цикл
, так как только у нее осталось нечетное число неиспользованных ребер. Таким образом, мы получили цикл  , если в него вошли все ребра графа, то теорема доказана. Если остались ребра графа, не вошедшие в цикл
, если в него вошли все ребра графа, то теорема доказана. Если остались ребра графа, не вошедшие в цикл  , то благодаря связности графа хотя бы одно из них должно быть инцидентно какой-либо вершине, вошедшей в
, то благодаря связности графа хотя бы одно из них должно быть инцидентно какой-либо вершине, вошедшей в  , назовем ее
, назовем ее  . Из вершины
. Из вершины  пойдем по неиспользованным ребрам, этот путь завершится в вершине
пойдем по неиспользованным ребрам, этот путь завершится в вершине  , получим цикл
, получим цикл  . Рассмотрим цикл
. Рассмотрим цикл  и
и  – последовательности вершин и ребер цикла
– последовательности вершин и ребер цикла  . Если в цикл
. Если в цикл  вошли все ребра графа
вошли все ребра графа 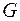 , то
, то  – эйлеров цикл, если нет, то повторим процедуру.
– эйлеров цикл, если нет, то повторим процедуру.
Определение. Граф называется полуэйлеровым, если в нем существует цепь, проходящая по всем ребрам по одному разу.
Теорема. Cвязный граф будет полуэйлеровым тогда и только тогда, когда в нем существуют ровно 2 вершины нечетной степени.
Теорема Дирака (достаточное условие гамильтоновости неориентированного графа).
Если 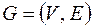 – связный простой граф с
– связный простой граф с  вершинами и для любой вершины
вершинами и для любой вершины 
 , то в нем существует гамильтонов цикл.
, то в нем существует гамильтонов цикл.
Доказательство. Пусть условия теоремы выполняются, тем не менее 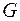 не является гамильтоновым графом, т. е. существует вершина
не является гамильтоновым графом, т. е. существует вершина 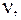 из которой нельзя попасть в вершину
из которой нельзя попасть в вершину  . Тогда добавим к графу
. Тогда добавим к графу 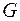
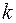 новых вершин, соединим их со всеми вершинами графа
новых вершин, соединим их со всеми вершинами графа  так, чтобы полученный граф
так, чтобы полученный граф  стал гамильтоновым, и пусть
стал гамильтоновым, и пусть  – минимальное число требуемых вершин.
– минимальное число требуемых вершин.
В  существует гамильтонов цикл:
существует гамильтонов цикл:  , где
, где 
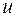 – вновь добавленная вершина. Удалить ее нельзя, так как вершины
– вновь добавленная вершина. Удалить ее нельзя, так как вершины 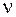 и
и  не являются смежными по предположению. C другой стороны, не может быть цикла вида
не являются смежными по предположению. C другой стороны, не может быть цикла вида  , где добавленные вершины
, где добавленные вершины  и
и  смежны, так как мы добавляем минимальное число новых вершин.
смежны, так как мы добавляем минимальное число новых вершин.
Не может быть и такого случая:  , где
, где  смежна с
смежна с 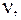 а
а  смежна с
смежна с  . В этом случае можно было бы перевернуть часть цикла от
. В этом случае можно было бы перевернуть часть цикла от  до
до  :
:  и обойтись без добавления вершины
и обойтись без добавления вершины  для получения гамильтонова цикла.
для получения гамильтонова цикла.
Число вершин в графе  , смежных с вершиной
, смежных с вершиной 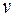 (или
(или  ) не меньше чем
) не меньше чем  , так как степень вершины не меньше чем
, так как степень вершины не меньше чем  , а добавленные вершины смежны со всеми вершинами графа по построению.
, а добавленные вершины смежны со всеми вершинами графа по построению.
Рассмотрим вершины, не смежные с  . Так как вершина
. Так как вершина  , смежная с
, смежная с  , не может идти в цикле сразу за вершиной
, не может идти в цикле сразу за вершиной  , смежной с
, смежной с 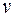 , то вершин, не смежных с
, то вершин, не смежных с  должно быть не меньше, чем вершин, смежных с
должно быть не меньше, чем вершин, смежных с 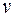 (в цепочке должно быть
(в цепочке должно быть  ), т. е. не меньше чем
), т. е. не меньше чем  Тогда общее число вершин в графе
Тогда общее число вершин в графе 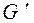 не меньше чем
не меньше чем  . C другой стороны, их ровно
. C другой стороны, их ровно  , отсюда
, отсюда  , и теорема доказана.
, и теорема доказана.
Деревья
Определение. Деревом называется связный граф без циклов.
Определение. Остовным деревом связного графа 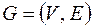 называется подграф
называется подграф  ,
,  , который является деревом.
, который является деревом.
Теорема о существовании остовного дерева. Из любого связного графа можно выделить остовное дерево.
Доказательство. Пусть 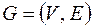 – связный граф, если в нем нет циклов, то он сам дерево. Пусть граф
– связный граф, если в нем нет циклов, то он сам дерево. Пусть граф 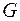 содержит цикл
содержит цикл  . Возьмем ребро
. Возьмем ребро  , рассмотрим граф
, рассмотрим граф  , граф
, граф  – связный (по лемме об удалении ребра из цикла), но количество циклов в нем уменьшилось, по крайней мере, на 1. Повторяя эту процедуру до тех пор, пока не разрушатся все циклы, мы получим связный граф без циклов – остовное дерево графа
– связный (по лемме об удалении ребра из цикла), но количество циклов в нем уменьшилось, по крайней мере, на 1. Повторяя эту процедуру до тех пор, пока не разрушатся все циклы, мы получим связный граф без циклов – остовное дерево графа 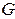 .
.
Теорема о числе ребер в дереве. Пусть 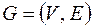 – дерево,
– дерево,  , тогда
, тогда  .
.
Доказательство. Так как в дереве нет циклов, то  . Дерево – связный граф, следовательно,
. Дерево – связный граф, следовательно, 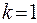 , тогда
, тогда  или
или  .
.
Теорема об эквивалентных определениях дерева. Пусть  ,
,  , тогда следующие утверждения попарно эквивалентны:
, тогда следующие утверждения попарно эквивалентны:
1. 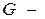 дерево, т. е. связный граф без циклов;
дерево, т. е. связный граф без циклов;
2. 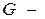 граф без циклов и
граф без циклов и  ;
;
3. 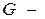 связный граф и
связный граф и  ;
;
4. 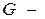 связный граф, но при удалении любого ребра становится несвязным;
связный граф, но при удалении любого ребра становится несвязным;
5.  граф без циклов, но при добавлении любого ребра в нем образуется цикл.
граф без циклов, но при добавлении любого ребра в нем образуется цикл.
Доказательство. Покажем, что из  .
.
 :
: 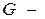 дерево, по теореме о числе ребер в дереве
дерево, по теореме о числе ребер в дереве  .
.
 : По лемме о числе связных компонент в графе без циклов
: По лемме о числе связных компонент в графе без циклов
 , у нас
, у нас  , т. е.
, т. е. 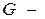 связный граф.
связный граф.
 : Если
: Если  и
и  , то
, то  , т. е.
, т. е.  граф
граф
несвязен.
 : Если в графе
: Если в графе  имеется цикл, то удаление ребра из цикла
имеется цикл, то удаление ребра из цикла
оставляет граф связным, что противоречит условию.
 :
: 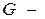 граф без циклов, надо показать, что он связен. Но если граф несвязен, то можно добавить ребро, соединяющее вершины из разных связных компонент, при этом не образуется цикл, что противоречит условию.
граф без циклов, надо показать, что он связен. Но если граф несвязен, то можно добавить ребро, соединяющее вершины из разных связных компонент, при этом не образуется цикл, что противоречит условию.
Заключение. Из двух последних утверждений следует, что дерево – минимальный связный граф, но максимальный граф без циклов.
Cреди деревьев особое место занимают корневые деревья, которые используются в процедурах поиска в информационных системах.
Дадим индуктивное определение корневого дерева.
1. Граф, имеющий единственную вершину 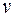 и пустое множество ребер, называется корневым деревом с корнем
и пустое множество ребер, называется корневым деревом с корнем 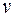 .
.
2. Пусть  – корневые деревья с корнями
– корневые деревья с корнями  и каждое
и каждое  . При этом
. При этом 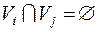 при
при  .
.
3. Пусть  , тогда граф
, тогда граф  , где
, где  и
и  , называется корневым деревом с корнем
, называется корневым деревом с корнем 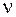 . Деревья
. Деревья  называются поддеревьями дерева
называются поддеревьями дерева  .
.
Определение. Упорядоченным корневым деревом называется корневое дерево  , в котором задан порядок его поддеревьев и каждое поддерево – упорядоченное дерево.
, в котором задан порядок его поддеревьев и каждое поддерево – упорядоченное дерево.
Получим оценку числа упорядоченных корневых деревьев. Для этого введем кодировку упорядоченных корневых деревьев. Кодировать будем согласно индуктивному определению корневого дерева.
1. Дереву  поставим в соответствие пустое слово.
поставим в соответствие пустое слово.
2. Пусть упорядоченное корневое дерево имеет поддеревья  и каждому поддереву
и каждому поддереву  поставлен в соответствие код
поставлен в соответствие код  .
.
3. Тогда кодом дерева  будет код
будет код  .
.
Так как корневыми деревьями являются только деревья, которые могут быть построены в соответствие с определением, то все они могут быть закодированы.
Из определения кода дерева следует, что код дерева – это слово из нулей и единиц.
Лемма о коде дерева. Пусть  – код упорядоченного корневого дерева
– код упорядоченного корневого дерева  . Обозначим через
. Обозначим через  – число нулей,
– число нулей,  – число единиц в коде,
– число единиц в коде,  – общее число символов. Пусть
– общее число символов. Пусть  , где
, где  и
и  два подслова. Тогда
два подслова. Тогда
а)  , где
, где  число ребер в дереве
число ребер в дереве  ;
;
б)  ;
;
в)  , причем равенство достигается только тогда, когда
, причем равенство достигается только тогда, когда  , где
, где  – коды первых
– коды первых  поддеревьев дерева
поддеревьев дерева  .
.
Доказательство. Доказательство проведем методом индукции по построению дерева  .
.
1. Если  , то его кодом является пустое слово, число ребер так же равно нулю, и все утверждения леммы становятся тривиальными.
, то его кодом является пустое слово, число ребер так же равно нулю, и все утверждения леммы становятся тривиальными.
2. Пусть дерево  имеет поддеревья
имеет поддеревья  , и для их кодов
, и для их кодов  все утверждения леммы справедливы.
все утверждения леммы справедливы.
3. Покажем, что они справедливы для кода дерева  . Пусть
. Пусть  число ребер в поддереве
число ребер в поддереве  , тогда число ребер в дереве
, тогда число ребер в дереве  будет равно
будет равно  .
.
а) 
так как по индуктивному предположению  .
.
б) По индуктивному предположению  , при построении кода
, при построении кода  добавляется равное число нулей и единиц,
добавляется равное число нулей и единиц,
отсюда  .
.
в) Если  , то очевидно,
, то очевидно,  . Пусть
. Пусть  имеет вид:
имеет вид:  , то есть
, то есть  . Найдем в этом случае
. Найдем в этом случае  .
.  , здесь s – количество 0, и
, здесь s – количество 0, и  ,
,  по индуктивному предположению, тогда
по индуктивному предположению, тогда
 , т. е.
, т. е.  , что и требовалось доказать.
, что и требовалось доказать.
Последнее утверждение позволяет в коде дерева выделить коды отдельных поддеревьев. Для этого надо найти точки, где количество нулей совпадает с количеством единиц, т. е. надо найти  и т. д. Затем в каждом
и т. д. Затем в каждом  проделать такую же процедуру. Таким образом, по коду упорядоченного корневого дерева можно восстановить само дерево.
проделать такую же процедуру. Таким образом, по коду упорядоченного корневого дерева можно восстановить само дерево.
Теорема о числе упорядоченных корневых деревьев. Число упорядоченных корневых деревьев с  ребрами не превосходит
ребрами не превосходит  .
.
Доказательство. Так как между упорядоченными корневыми деревьями и их кодами существует биекция, то их число равно числу кодов деревьев. Код дерева с 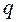 ребрами – слово длины
ребрами – слово длины  , состоящее из нулей и единиц.
, состоящее из нулей и единиц.
Число кодов не превосходит общего числа слов длины  , состоящих из 0 и 1, которое равно
, состоящих из 0 и 1, которое равно  . Таким образом, число упорядоченных корневых деревьев с
. Таким образом, число упорядоченных корневых деревьев с  ребрами не превосходит
ребрами не превосходит  .
.
Следствия:
1. Число попарно неизоморфных неупорядоченных корневых деревьев с  ребрами не превосходит числа упорядоченных корневых деревьев и, следовательно, не превосходит
ребрами не превосходит числа упорядоченных корневых деревьев и, следовательно, не превосходит  .
.
2. Число попарно неизоморфных деревьев с  ребрами не превосходит числа корневых деревьев с
ребрами не превосходит числа корневых деревьев с  ребрами, так как они различаются выбором корневой вершины, следовательно, не превосходит
ребрами, так как они различаются выбором корневой вершины, следовательно, не превосходит  .
.
Пример. Деревья, приведенные на рис. 5.12, попарно изоморфны, но различны с точки зрения корневых деревьев.
 Рис. 5 .12
Рис. 5 .12
|
Задача о соединении городов. Пусть есть 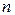 городов, расстояние между каждыми двумя городами известно. Надо соединить их дорогой минимальной длины (или минимальной стоимости, если известна цена дороги между каждыми двумя городами).
городов, расстояние между каждыми двумя городами известно. Надо соединить их дорогой минимальной длины (или минимальной стоимости, если известна цена дороги между каждыми двумя городами).
Эту задачу можно сформулировать на языке теории графов, полагая города вершинами, а расстояния – ребрами графа. Пусть каждому ребру графа поставлено в соответствие положительное число  , называемое мерой ребра (расстояние между городами или стоимость прокладываемой дороги). Обозначим меру графа
, называемое мерой ребра (расстояние между городами или стоимость прокладываемой дороги). Обозначим меру графа 
 .
.
Стоит следующая задача: дан простой полный граф на 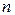 вершинах, задана мера каждого ребра, надо построить связный подграф минимальной меры. (Требование полноты исходного графа необязательно, достаточно, чтобы он был связным). Очевидно, что минимальный связный граф – дерево, поэтому задачу можно уточнить: построить остовное дерево минимальной меры.
вершинах, задана мера каждого ребра, надо построить связный подграф минимальной меры. (Требование полноты исходного графа необязательно, достаточно, чтобы он был связным). Очевидно, что минимальный связный граф – дерево, поэтому задачу можно уточнить: построить остовное дерево минимальной меры.
Алгоритм Краскала построения остовного дерева минимальной меры.
Выберем ребро минимальной меры, обозначим его 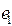 . Если несколько ребер имеют одну и ту же меру, берем любое. Затем выбираем ребро минимальной меры из оставшихся, обозначим его
. Если несколько ребер имеют одну и ту же меру, берем любое. Затем выбираем ребро минимальной меры из оставшихся, обозначим его 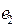 . Затем выбираем ребро минимальной меры из оставшихся, но так, чтобы оно не образовывало цикла с выбранными ранее ребрами. Выбрав таким образом
. Затем выбираем ребро минимальной меры из оставшихся, но так, чтобы оно не образовывало цикла с выбранными ранее ребрами. Выбрав таким образом  ребро, получим остовное дерево
ребро, получим остовное дерево  , причем
, причем
 .
.
Покажем, что не будет остовных деревьев с мерой меньшей, чем мера дерева  .
.
Пусть есть остовное дерево  такое, что
такое, что  . Пусть
. Пусть 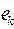 – первое ребро из T, не вошедшее в S. Рассмотрим граф
– первое ребро из T, не вошедшее в S. Рассмотрим граф  , он не является деревом, следовательно, в нем существует цикл
, он не является деревом, следовательно, в нем существует цикл 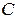 . Пусть
. Пусть  и
и  , такое ребро существует, так как
, такое ребро существует, так как  – дерево, и не содержит циклов. Удалив это ребро из графа
– дерево, и не содержит циклов. Удалив это ребро из графа  , получим граф
, получим граф  , он – связный граф, в нем
, он – связный граф, в нем  ребро, следовательно, он – дерево. При этом графы T и
ребро, следовательно, он – дерево. При этом графы T и  содержат на одно общее ребро больше, чем графы T и S.
содержат на одно общее ребро больше, чем графы T и S.
 ,
,
так как  , иначе при построении дерева
, иначе при построении дерева  по алгоритму Краскала мы вместо ребра
по алгоритму Краскала мы вместо ребра  взяли бы ребро
взяли бы ребро  (ребра
(ребра  у деревьев T и S общие и
у деревьев T и S общие и  не образует с ними цикла).
не образует с ними цикла).
Пусть  – следующее ребро из
– следующее ребро из  , не вошедшее в
, не вошедшее в  . Присоединим его к графу
. Присоединим его к графу  , вновь образуется цикл, удалим из него ребро
, вновь образуется цикл, удалим из него ребро  и
и  . Получим граф
. Получим граф  этот граф и граф
этот граф и граф  будут иметь на 2 общих ребра больше, чем графы
будут иметь на 2 общих ребра больше, чем графы  и
и  , при этом
, при этом

 .
.
Повторив эту процедуру конечное число раз, перестроим граф  в
в  и получим противоречие
и получим противоречие
 .
.
Пример. C помощью алгоритма Краскала найти остовное дерево минимальной меры в графе (рис. 5.13).
 Рис. 5 .13 Рис. 5 .14
Рис. 5 .13 Рис. 5 .14
|
Определение. Циклическим рангом связного графа (или цикломатическим числом)  называют число ребер, которые необходимо убрать, чтобы граф стал деревом.
называют число ребер, которые необходимо убрать, чтобы граф стал деревом.
Если  и так как в дереве число ребер
и так как в дереве число ребер  , то
, то  .
.
Дата: 2019-04-23, просмотров: 433.