1. Идемпотентность & и Ú: х&x = x, xÚx = x.
2. Коммутативность &, Ú, Å, |, ~, 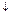 .
.
3. Aссоциативность &, Ú, Å, ~, поэтому в формулах вида xyz можно не ставить никаких скобок.
4. Дистрибутивность:
а) & по отношению к Ú: x&(yÚz) = xyÚxz ,
б) Ú по отношению к &: xÚ(y&z) = (xÚy)&(xÚz) ,
в) & по отношению к Å: x(yÅz) = xyÅxz .
5. Инволюция:  .
.
6. Правила де Моргана:  =
=  &
&  и
и  =
=  Ú
Ú  .
.
7. Законы действия с 0 и 1:
xÚ0 = x, xÚ1 = 1, x&0 = 0, x&1 = x, xÅ1 =  , xÅ0 = x.
, xÅ0 = x.
8. Cамодистрибутивность импликации:
x  (y
(y  z) = (x
z) = (x  y)
y)  (x
(x  z) (табл. 3.12).
z) (табл. 3.12).
Равенство всех этих формул доказывается по определению, т. е. по равенству функций, которые они реализуют.
Проверим для примера самодистрибутивность импликации:
x  (y
(y  z) = (x
z) = (x  y)
y)  (x
(x  z) (табл. 3.12).
z) (табл. 3.12).
Таблица 3.12
| x | y | z | y 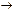 z z
| x 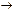 (y (y 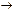 z) z)
| x 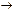 y y
| x 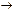 z z
| 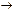
|
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 1 1 0 1 1 1 0 1 | 1 1 1 1 1 1 0 1 | 1 1 1 1 0 0 1 1 | 1 1 1 1 0 1 0 1 | 1 1 1 1 1 1 0 1 |
Следствия из свойств элементарных функций
1. Законы склеивания:
xyÚx  = x(yÚ
= x(yÚ  ) = x
) = x 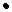 1 = x (дистрибутивность & относительно Ú);
1 = x (дистрибутивность & относительно Ú);
(xÚy)&(x  ) = x
) = x  •y = xÚ 0 = x (дистрибутивность Ú относительно &).
•y = xÚ 0 = x (дистрибутивность Ú относительно &).
2. Законы поглощения:
xÚxy = x(1Úy) = x 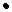 1 = x; x&(xÚy) = xÚxy = x.
1 = x; x&(xÚy) = xÚxy = x.
Cвойства элементарных функций позволяют упрощать формулы.
Пример 7 . Упростим формулы:
1. x2x3Úx1  2x3 = x3(x2Úx1
2x3 = x3(x2Úx1  2) = x3((x2Úx1)&(x2Ú
2) = x3((x2Úx1)&(x2Ú  2)) = (x1Úx2)x3.
2)) = (x1Úx2)x3.
2. x1Ú  1x2Ú
1x2Ú  1
1  2 x3Ú
2 x3Ú  1
1  2
2  x4 = x1Ú
x4 = x1Ú  1 (x2Ú
1 (x2Ú  2 x3Ú
2 x3Ú  2
2  3 x4) =
3 x4) =
= (x1Ú  1)(x1Úx2Ú
1)(x1Úx2Ú  2 x3Ú
2 x3Ú  2
2  3 x4) = x1Úx2Ú
3 x4) = x1Úx2Ú  2
2 
= x1Ú(x2Ú  )(x2Úx3Ú
)(x2Úx3Ú  x4) = x1Úx2Úx3Úx4.
x4) = x1Úx2Úx3Úx4.
3. Принцип двойственности
Определение. Функция f *(x1, ..., xn) называется двойственной к функции f(x1, ..., xn), если f*( x1, ..., xn) =  (
(  1, ...,
1, ...,  n).
n).
Пример 8. Покажем с помощью таблицы истинности (табл. 3.13), что константа 0 двойственна к 1.
Таблица 3.13
| x | f | f* |
| 0 1 | 0 0 | 1 1 |
Функции f(x) = x и g(x) =  двойственны сами себе (табл. 3.14).
двойственны сами себе (табл. 3.14).
Таблица 3.14
| x | f | f* | g | g* |
| 0 1 | 0 1 | 0 1 | 1 0 | 1 0 |
Определение. Если f*(x1, ..., xn) = f(x1, ..., xn), то f(x1, ..., xn) называется самодвойственной.
Если f* – самодвойственна, то  (
(  1, ...,
1, ...,  n) = f(x1, ..., x n), т. е. на противоположных наборах функция принимает противоположные значения.
n) = f(x1, ..., x n), т. е. на противоположных наборах функция принимает противоположные значения.
Пример 9. Покажем, что f(x1, x2, x3) = x1Åx2Åx3 – самодвойственна (табл. 3.15).
Таблица 3. 15
| x1 | x2 | x3 | f | f* |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 1 1 0 1 0 0 1 | 0 1 1 0 1 0 0 1 |
Пример 10. Покажем, что функция x1&x2 двойственна к x1Úх2, функция x1  х2 двойственна к функции x1|x2 (табл. 3.16).
х2 двойственна к функции x1|x2 (табл. 3.16).
Таблица 3. 16
| x1x2 | f = x1Úх2 | f* | g = x1|x2 | g* = x1 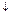 x2 x2
|
| 0 0 0 1 1 0 1 1 | 0 1 1 1 | 0 0 0 1 | 1 1 1 0 | 1 0 0 0 |
Теорема о двойственных функциях. Если f* двойственна к f, то f двойственна к f*.
Доказательство. f*( x1, ..., x n) =  (
(  1, ...,
1, ...,  n). Найдем двойственную функцию к f*, т. е. (f*( x1, ..., x n))* = (
n). Найдем двойственную функцию к f*, т. е. (f*( x1, ..., x n))* = (  (
(  1, ...,
1, ...,  n))* =
n))* =
=  (
(  1, ...,
1, ...,  n) = f(x1, .., x n).
n) = f(x1, .., x n).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Принцип двойственности
Теорема. Пусть функция h(x1, ..., xn) реализована формулой h(x1, ..., x n) = g(G1, ..., G m) = g(f1(x1, ..., x n), ..., fm(x1, ..., x n)), где какие-то переменные могут быть фиктивными. Тогда
h*( x1, ..., x n) = g*(f1*( x1, ..., x n), ..., fm*(x1, …, x n)), это означает, что если функция задана некоторой формулой, то, чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные:  на
на  и наоборот,
и наоборот,  на ~ и наоборот, | на
на ~ и наоборот, | на  и наоборот, 0 на 1 и наоборот. Двойственная к
и наоборот, 0 на 1 и наоборот. Двойственная к  находится следующим образом:
находится следующим образом:  .
.
Доказательство теоремы. h*(x1, ..., xn) =  (
(  , ...,
, ...,  ) =
) =
=  (f1(
(f1(  , ...,
, ...,  ), ..., fm(
), ..., fm(  , ...,
, ...,  )) =
)) =
=  (
(  (
(  , ...,
, ...,  ), ..., fm(
), ..., fm(  , ...,
, ...,  )) =
)) =
=  ((
((  ), ...,((
), ...,((  )=
)=
= g*(f1*(x1, ..., xn), ... , fm*(x1, ... , xn)),
что и требовалось доказать.
Если функция h(x1, ..., x n) реализуется формулой N [f1, ..., f n], то формулу, полученную из N заменой fi, входящих в нее, на f i* и реализующую функцию h*(x1, ... , x n), будем называть двойственной и обозначать N*(x1, ... , x n).
Пример 11. Найти двойственную функцию к  .
.
По принципу двойственности

 .
.
Дата: 2019-04-23, просмотров: 229.