Отношение эквивалентности
Пусть A и В – множества.
Определение. Произведением множеств А и В называется множество всех упорядоченных пар (а, b), где аÎА и bÎВ. Произведение обозначается А ´ В.
А ´ В = {(a, b): aÎA и bÎB}.
Произведение двух множеств часто называют прямым или декартовым произведением. Заметим, что произведение 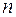 штук одного и того же множества А обозначается через
штук одного и того же множества А обозначается через 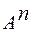 .
.
Примеры. 1) Если А = {a, b}, B = {0, 1}, C = Æ,
то А ´ В = {(a, 0), (a, 1), (b, 0), (b, 1)},
B ´ A = {(0, a) (0, b), (1, a), (1, b)},
A ´ C = C´A = Æ.
2) Пусть R – множество действительных чисел. Тогда 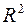 – множество, которое обычно изображается в виде плоскости, а элементы из
– множество, которое обычно изображается в виде плоскости, а элементы из 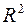 называются точками плоскости.
называются точками плоскости.
3) Пусть [a, b], [c, d] – отрезки прямой. Тогда [a, b] ´ [c, d] – прямоугольник на плоскости.
Определение. Бинарным отношением (или просто отношением) в А ´ В называется любое подмножество множества А ´ В.
Примеры. 1) Пусть А = {1, 2, 3}, B = {1, 2, 3, 4, 5, 6, 7}. Тогда A ´ B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (2, 7), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (3, 7)}.
Возьмем S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6)}. Ясно, что SÍA ´ B, т. е. S является бинарным отношением в A ´ B. Это отношение может быть охарактеризовано следующей формой
S = {(x, y)ÎA ´ B: xÎA является делителем yÎB}.
2) Пусть А некоторое множество, а b(А) множество всех его подмножеств. Множество b(А) называется булеаном. Пусть W отношение в b(А) ´ b(А), задаваемое формой:
W = {(B, C)Îb(A) ´ b(A) : BÍC}.
Тогда W является отношением включения множеств.
Если S является некоторым отношением и (x, y)ÎS, то мы будем писать x Sy и говорить, что x находится в отношении S с y.
Если S является отношением в А ´ А, то говорят, что S является отношением в А.
Пусть S некоторое отношение в А ´ В. Введем два множества:
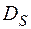 = {aÎA: $ bÎB: (a, b)ÎS},
= {aÎA: $ bÎB: (a, b)ÎS},
 = {bÎB: $ aÎA: (a, b)ÎS}.
= {bÎB: $ aÎA: (a, b)ÎS}.
Множество 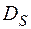 называется областью определения отношения, а множество
называется областью определения отношения, а множество  – областью значений. Если
– областью значений. Если 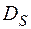 = A, то такое отношение называют всюду определенным, а если
= A, то такое отношение называют всюду определенным, а если  = B – сюръективным. Когда отношение одновременно является сюръективным и всюду определенным, то говорят, что S отношение на А ´ В (соответственно на А, если В = А).
= B – сюръективным. Когда отношение одновременно является сюръективным и всюду определенным, то говорят, что S отношение на А ´ В (соответственно на А, если В = А).
Отношение S называется инъективным, если из (a, b)ÎS и (c, b)ÎS следует, что а = с.
Иногда отношения называются соответствием между элементами множества А и В.
Пусть S некоторое отношение в А ´ В. Введем отношение 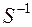 следующим образом: (у, х)Î
следующим образом: (у, х)Î  Û(х, у)ÎS. Отношение
Û(х, у)ÎS. Отношение  назовем обратным отношением.
назовем обратным отношением.
Определение. Отношение S на множестве А называется отношением эквивалентности, если оно удовлетворяет следующим условиям:
1) а Sа для " аÎА (рефлексивность);
2) если а Sв, то в Sа (симметричность);
3) если а Sв и в Sс, то а Sс (транзитивность).
В дальнейшем отношение эквивалентности будем обозначать значком.
Определение. Пусть задано отношение эквивалентности на А. Множество ХÍА называется классом эквивалентности для этого отношения, если оно удовлетворяет следующим условиям:
1) для любых хÎХ и уÎХ выполняется х»у;
2) если хÎХ , уÎА и х»у, то уÎХ.
Пусть на А задано отношение эквивалентности. Введем следующее обозначение:
[x = {yÎA: x»y}.
Нетрудно видеть из определений, что [x] является классом эквивалентности. Его называют классом эквивалентности, порожденным элементом х.
Лемма 1. Для классов эквивалентности [x] и [y] возможны только следующие два случая:
1) [x] = [y];
2) [x]Ç[y] = Æ.
Доказательство. Предположим, что [x]Ç[y]¹Æ и аÎ[x]Ç[y]. Тогда x»a и y»a. Покажем, что в этом случае один класс эквивалентности содержится в другом, а так как они равнозначны, то будет доказано равенство этих классов.
Пусть вÎ[x]. Тогда х»в, а»х, следовательно в»а. Но а»y, значит в»y и вÎ[y], т. е. [x]Í[y].
Пусть некоторое множество А представимо в виде:
А = 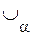 А, где
А, где 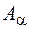 Ç
Ç 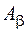 = Æ , если a ¹ b.
= Æ , если a ¹ b.
В этом случае говорят, что { 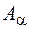 } задает разбиение А. Из доказанной леммы вытекает, что классы эквивалентности задают разбиение на А. Оказывается, верно и обратное.
} задает разбиение А. Из доказанной леммы вытекает, что классы эквивалентности задают разбиение на А. Оказывается, верно и обратное.
Лемма 2. Если { 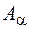 } – некоторое разбиение множества А, то отношение S, определяемое следующим условием: а SвÛ$a: аÎ
} – некоторое разбиение множества А, то отношение S, определяемое следующим условием: а SвÛ$a: аÎ 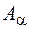 и вÎ
и вÎ 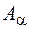 , является отношением эквивалентности.
, является отношением эквивалентности.
Доказательство. По существу, в доказательстве нуждается лишь третье свойство эквивалентности. Пусть а Sв и вSс. Тогда из задания отношения S вытекает следующее: $a: аÎ 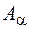 и вÎ
и вÎ 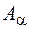 , а также $b: вÎ
, а также $b: вÎ 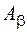 и сÎ
и сÎ 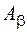 . Тогда вÎ
. Тогда вÎ 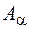 Ç
Ç 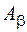 и из свойств разбиения следует, что
и из свойств разбиения следует, что 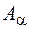 =
= 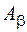 или a = b, следовательно, аÎ
или a = b, следовательно, аÎ 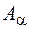 и сÎ
и сÎ 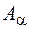 . Это доказывает, что а Sс и отношение S является отношением эквивалентности.
. Это доказывает, что а Sс и отношение S является отношением эквивалентности.
Теорема. Пусть S – некоторое отношение эквивалентности на А. Пусть { 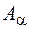 } – разбиение множества А, порожденное этим отношением (лемма 1). Пусть Т – отношение эквивалентности, порожденное разбиением {
} – разбиение множества А, порожденное этим отношением (лемма 1). Пусть Т – отношение эквивалентности, порожденное разбиением { 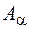 } (лемма 2). Тогда S = T.
} (лемма 2). Тогда S = T.
Доказательство. Для доказательства напомним, что S и T являются подмножеством А ´ А и их равенство понимается как равенство множеств. Пусть (а, в)ÎS, т. е. аSв. Тогда а и в из одного класса эквивалентности, т. е. $a: аÎ 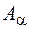 и вÎ
и вÎ 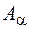 . Это означает, что (а, в)ÎT и SÍT. Aналогично показывается обратное включение.
. Это означает, что (а, в)ÎT и SÍT. Aналогично показывается обратное включение.
Задачи.
1. Доказать, что существуют А, В и С такие, что
а) А ´ В ¹ В ´ А;
б) А ´ (В ´ С) ¹ (А ´ В) ´ С.
2. Доказать, что если А, В, С и D не пусты, то
а) АÍВ и СÍDÛА ´ СÍВ ´ D;
б) А = В и С = DÛA ´ C = B ´ D.
3. Доказать, что
а) (АÇВ) ´ (СÇD) = (А ´ С)Ç(В ´ D);
б) (А ´ В)È(C ´ D)Í(AÈC) ´(BÈD);
в) (АÈВ) ´ С = (А ´ С)È(В ´ С);
г) А ´ (ВÈС) = (А ´ В)È(А ´ С);
д) (АÈВ) ´ (CÈD) = (A ´ C)È(B ´ C)È(A ´ D)È(B ´ D);
е) (А – В) ´ С = (А ´ С) – (В ´ С);
ж) А ´ (В – С) = (А ´ В) – (А ´ С);
з) А ´ В = (A ´ D) Ç (C ´ B), где АÍС и BÍD.
4. Найти область определения и область значений для отношений:
а) R={(x, y): x, yÎN и x делит y};
б) R={(x, y): x, yÎN и y делит x};
в) R={(x, y): x, yÎR и x + y ³ 0};
г) R={(x, y): x, yÎR и 2x > 3y}.
5. Пусть S отношение в А ´ В, а R – в В´С. Через SoR (суперпозиция отношений) обозначается отношение в А ´ С, определяемое равенством SoR = {(x, y)ÎA ´ C: $ zÎB: (x, z)ÎS и (z, y)ÎR}.
Пусть R, S, T – некоторые отношения. Проверить справедливость равенств:
а) Ro(SoT) = (RoS)oT;
б) 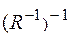 = R;
= R;
в) (RoS)–1 = 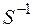 o
o  .
.
6. Пусть на множестве А заданы отношения 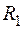 и
и 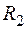 . Доказать:
. Доказать:
а) если отношения 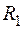 и
и 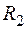 рефлексивны, то рефлексивны отношения
рефлексивны, то рефлексивны отношения 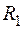 È
È 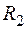 ,
, 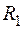 Ç
Ç 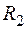 ,
,  ,
, 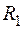 o
o 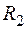 ;
;
б) если отношения 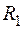 и
и 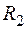 иррефлексивны (т. е. для "хÎА не выполняется х R х), то иррефлексивны
иррефлексивны (т. е. для "хÎА не выполняется х R х), то иррефлексивны 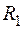 È
È 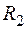 ,
, 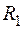 Ç
Ç 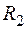 ,
, 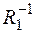 , суперпозиция
, суперпозиция 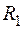 о
о 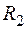 может быть иррефлексивной;
может быть иррефлексивной;
в) если отношения 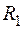 и
и 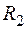 симметричны, то симметричны отношения
симметричны, то симметричны отношения 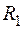 È
È 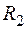 ,
, 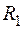 Ç
Ç 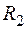 ,
,  ,
, 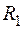 о
о 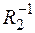 ;
;
г) отношение 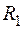 о
о 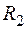 , где
, где 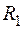 и
и 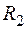 симметричны, симметрично тогда и только тогда, когда
симметричны, симметрично тогда и только тогда, когда 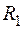 о
о 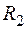 =
= 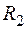 о
о 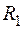 ;
;
д) если отношения 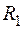 и
и 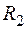 антисимметричны, то антисимметричны
антисимметричны, то антисимметричны 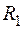 Ç
Ç 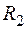 ,
,  .
.
7. Пусть А ‒ конечное множество, n – число его элементов. Доказать, что число подмножеств множества А, состоящих из m элементов, где 0 £ m £ n, равно
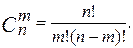
8. Пусть r – отношение, обладающее свойством рефлексивности и транзитивности в множестве А. Определим для а, bÎА отношение R, полагая а Rb, если аrb и brа.
а) Доказать, что R есть отношение эквивалентности на А.
в) Доказать, что если а Rа', b Rb' и а rb, то а'rb'.
9. Во множестве Z+ ´ Z+ положим по определению (а, b) r (с, d), если а + d = b + с. Доказать, что r является отношением эквивалентности на данном множестве.
| «Понятие функции такое же основное, как и понятие множества». Хаусдорф |
Функция
Пусть Х и У два множества и F отношение в Х ´ У.
Определение. Отношение F называется функцией из Х в У, если оно удовлетворяет свойству: из x Fy и x Fz следует, что y = z.
В дальнейшем мы будем применять также обозначение y = F(x) вместо x Fy, если F является функцией. Множества D F и R F, введенные в предыдущем пункте для функции F носят соответственно названия: D F – область определения и R F – область значений функции F. Очень часто область определения и область значений заранее не задаются, а возникают, исходя из задания функции.
Примеры.
1) {(1,2), (2,2), (Рузвельт, Черчилль)};
2) {(1,2), (1,3), (2,2)};
3) {(x, x2 + x + 1)|xÎR};
4) {(x2, x)|xÎR}.
Из приведенных примеров 1 и 3 определяют функцию, а 2 и 4 не являются функцией, так как не выполнено определение функции.
Для функции применяются также другие названия: преобразование, отображение, соответствие. Если y = F(x), то x называют аргументом функции, а y образом.
Две функции F и G считаются равными, если выполнены равенства соответствующих множеств. Последнее эквивалентно следующим двум равенствам:
DF = DG и F(x) = G(x) для "xÎDF .
Следующие определения переносятся с отношений:
1) В случае, когда D F = Х функцию называют всюду определенной.
2) Функция F из Х в Y называется сюръекцией (или отображением на), если R F = Y.
3) Функция F из Х в Y называется инъекцией (или однозначным отображением), если из х1¹х2 следует, что F(х1) ¹ F(х2).
Всюду определенная функция F из Х в Y называется биекцией, если она одновременно является сюръекцией и инъекцией.
Примеры: 1) функция у = е x – биекция из R в R+;
2) у = х2 – сюръекция из [–1, 1] на [0, 1], не являющаяся инъекцией.
Определение. Пусть F – функция из X в Y, а G – из Y в Z. Суперпозицией функций F и G называется такая функция H из X в Z, что z = H(x) (т. е. (x, z)ÎHÍX ´ Z) тогда и только тогда, когда y = F(x) и z = G(y). Cуперпозиция обозначается GoF.
Определение. Для функции F из Х в Y функция G из Y в Х называется правой обратной (соответственно левой обратной, если справедливо равенство FoG=I Y (соответственно G o F = IХ), где через I Х (I Y) обозначено тождественное отображение на Х (соответственно на Y), т. е. I Х(x) = x (I Y(y) = y).
Функция у = х2, из рассмотренного выше примера не имеет левой обратной, но имеет правую обратную (ею является функция х= 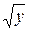 ). Однако если сузить область определения функции у = х2 до отрезка [0,1] (или [–1,0]), оставив без изменений область значений, то эта функция будет иметь уже и левую обратную: х =
). Однако если сузить область определения функции у = х2 до отрезка [0,1] (или [–1,0]), оставив без изменений область значений, то эта функция будет иметь уже и левую обратную: х = 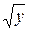 (соответственно, х = –
(соответственно, х = – 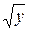 ).
).
Лемма 1. Если функция F имеет левую обратную, то F является инъекцией.
Доказательство. Действительно, если бы F не являлась инъекцией, то существовали бы х1¹х2 такие, что y = F(x1) = F(x2). Пусть G – левая обратная к F, то x1 = G o F(x1) = G(y) = G o F(x2) = x2, что противоречит предположению.
Лемма 2. Если функция F имеет правую обратную, то F является сюръекцией.
Доказательство. Утверждение легко вытекает из определения правой обратной функции G: для любого уÎYÞFoG(у) = у.
Лемма 3. Если у функции F из Х в Y существуют левая и правая обратная функции, то они совпадают.
Доказательство. Пусть G и H – обозначают соответственно левую и правую обратную функции к F. Тогда D G = RF = DH = Y. Остается проверить равенство G(y) = H(y) для любого yÎY. Но (y) = G(I Y(y)) = G(F(H(y))) = I Х(H(y)) = H(y).
Определение. Функция из Y в Х, которая является правой и левой обратной к функции F, называется обратной функцией к F и обозначается через F –1.
Теорема. Пусть F является функцией из Х в Y. Для существования обратной функции F–1 из Y в Х необходимо и достаточно, чтобы F была биекцией.
Необходимость легко вытекает из лемм 1 и 2.
Достаточность. Пусть yÎY. Так как F является сюръекцией, то существует хÎХ такое, что F(x) = y. При этом такое х одно, так как F также и инъекция. Определим функцию G(x) = y. Легко проверить, что таким образом определенная функция является обратной к F.
Следствие. Если F является биекцией, то и F–1 также является биекцией.
Задачи.
1. Установить, что следующие отношения являются функцией:
а) bÎУ, R = X ´ {в}ÍX ´ У (постоянное отображение);
б) R = {(x, x): xÎX}ÍX ´ X (тождественное отображение IX);
в) R = {((x, y), x)}Í(X ´ Y) ´ X (проекция на Х);
г) R = {((x, y), у)}Í(X ´ Y) ´ Y (проекция на Y).
2. Пусть A – произвольное множество из области определения функции f(х). Верно ли равенство f –1 [f(A)] = A всегда ?
3. Пусть В – произвольное множество из области значений функции f(х). Верно ли равенство: f[f –1 (B)] = B всегда ?
4. Верны ли равенства:
f(AÈB) = f(A)Èf(B);
f(AÇB) = f(A)Çf(B)?
5. Верно ли, что f(R – A) = f(R) – f(A), где R – область определения функции?
6. Пусть A и В – два множества из области значений функции
у = f(х). Верны ли равенства:
f –1 (AÇB) = f –1 (A)Ç f –1 (B),
f –1 (AÈB) = f –1 (A)È f –1 (B)?
7. Пусть L – область значений функции у = f(х), а AÍL. Cправедливо ли равенство: f –1(L – A) = f –1 (L) – f –1 (A)?
8. Задана функция f из A в В. Доказать, что для всякого МÍВ справедливо включение f[f –1(M)]ÍM. Пусть ЕÍA. Доказать, что f –1 [f(E)]ÊE.
9. Задана функция f из A в В. Пусть Е 1ÍA, Е2ÍA, М 1ÍВ, М 2ÍВ. Доказать, что если Е 1ÍЕ2, то f(Е 1)Íf(Е 2), если М 1ÍМ2, то f –1(М 1)Í f–1 (М2).
10. Задана функция f из A в В. Доказать, что следующие условия попарно эквивалентны:
а) f – инъекция;
б) f –1 (f(Е)) = Е для любого ЕÍA;
в) f(ЕÇМ) = f(Е)Çf(М) для любых Е, МÍA;
г) f(Е)Çf(М) = Æ для любой пары множеств ЕÍA, МÍA такой, что ЕÇМ= Æ;
д) F(Е – М) = f(Е) – f(М) для любой пары множеств ЕÍA, МÍA такой, что МÍЕ.
11. Пусть даны множества A, В, С, D и функции
f: A ® В, g: В ® С, h: С ® D.
Доказать, что если каждая из суперпозиций gof и hog есть биекция, то и все функции f, g и h являются биекциями.
12. Пусть A – конечное множество и f функция из A в A. Доказать, что:
а) если f является сюръекцией, то f также и инъекция;
б) если f является инъекцией, то f также и сюръекция.
13. Построить отношения, удовлетворяющие следующим требованиям:
а) рефлексивное, симметричное, не транзитивное;
б) рефлексивное, транзитивное, не симметричное;
в) симметричное, транзитивное, не рефлексивное.
Дата: 2019-04-23, просмотров: 170.