Комбинированный метод хорд и касательных
а=
0
b=
1
ε=
0,01
х_неп=
1
f(x_неп)=
0,459698
a(Xорд)
B(Kасат)
Δ.
0
0
0,5
0,5
>
0,01
1
0,685
0,755
0,070149
>
0,01
2
0,736
0,739
0,002843
>
0,01
3
0,739
0,739
0,00014
<
0,01
4
0,739
0,739
7E-06
<
0,01
Как видно из таблицы на 3 -ей итерации получен корень уравнения, равный x=(a3+b3)/2=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0.685,0.755]+ É -[0.736,0.739]+ É -[0.739,0.739]+ É 0.739.
Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
Использование математического пакета MathCad в расчетах
По поиску корней уравнения
MathCad позволяет находить корни любого уравнения с одним неизвестным f(x) = 0 в численном виде, а для многих уравнений и в аналитическом (символьном виде). Если уравнение можно решить аналитически, то приводятся сразу все корни (исключая тригонометрические уравнения, где приводится один корень). Если же уравнение решается численно, то целесообразно вначале локализовать корень, то есть выделить отрезок существования лишь одного пересечения графика функции y = f(x) с осью абсцисс.
Для решения уравнения в аналитическом виде используется оператор solve, вызываемый с панели инструментов Solving(«Символика»), при этом уравнение в левой части оператора solve необходимо вводить в виде f(x)=0, где знак «=» вводится с панели булевых операторов.
Пример 4.2.
Найти решение уравнения из примера 4.1.
Решение.
Как видно, решение уравнения совпадает с ранее найденным различными численными методами. Тот же ответ дает использование оператора root :
Приведенное решение показывает, что вначале необходимо ввести начальное приближение к корню, если же необходимо найти корень на отрезке , то функция root может быть записана иначе:
Получаемый ответ тот же.
Помимо root, для f(x), имеющих вид полинома, можно использовать функцию polyroots, которая позволяет найти все корни уравнения f(x)=0, включая комплексные, но в качестве аргумента используется не функция f(x), а вектор коэффициентов полинома, начиная со свободного.
Пример 4.3.
Для функции f(x) = x2 - 10x + 13 найти корни.
Решение.
Функция является левой частью уравнения (1) для матрицы из примера 3.2:
Полученное решение совпадает с уже найденным.
Задания для лабораторной работы №4:
Задание 1.
а) Известно, что вещество С расходуется в мономолекулярной реакции с константой скорости k=8,2*10-2 с-1. Начальное значение концентрации вещества С равно N*10-2. Определить аналитическую зависимость для концентрации вещества С от времени реакции и найти такое время, при котором значение концентрации вещества С было бы равно N*10-3.
Примечание. Для решения задачи принять: а=25 с, b=35 c, e=0,001.
б) Найти решение скалярного уравнения: y = sin(N) + lg(x) + x – 10,5, a=8, b=12, e=0.001.
Задание 2.
а) - Построить в редакторе EXCEL (GNUPLOT) графическую зависимость C(t), ограничив время реакции 45 сек.
- Табулирование функции вести с шагом по t, равным 3 с.
- Шкала графика по оси C имеет:
максимальное значение = 3/2* N*10-2;
минимальное значение = -3/2* N*10-2
цена основного деления = 5* N*10-3.
б) Построить в редакторе GNUPLOT график функции y(x) на промежутке [a,b] с шагом по сетке, равным (b-a)/10. Добавить на рисунок надпись «Точка пересечения графика функции y(x)=… с осью Ох есть точка х=…».
Задание 3.
Найти решение задач в MathCad:
а) из задания 1 а) путем использования функции root с локализацией и без локализации корня, приняв за начальное приближение t=0;
б) из задания 1 б) путем использования функции root с локализацией и без локализации корня, приняв за начальное приближение х=25;
в) в обоих случаях построить графики функций на соответствующих отрезках: a) [0;45]; б) [25;35].
Контрольные вопросы
1. Сформулируйте теорему о существовании нуля непрерывной функции.
2. Какие случаи поведения функции возможны на выбранном отрезке.
3. Назовите суть метода бисекции.
4. Как рассчитать количество итераций при поиске корня заданного уравнения, используя метод бисекции?
5. Назовите суть метода итераций.
6. Для каких функций подходит метод итераций при поиске нуля функции?
7. Какая формула применяется для остановки работы алгоритма метода итераций?
8. Назовите суть метода хорд.
9. Назовите суть метода касательных.
10. В чем преимущество комбинированного метода хорд и касательных?
ТЕМА 5. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
На отрезке [a,b] рассматривается функция y=f(x), значения которой определены лишь в конечном числе точек. Эти точки образуют на отрезке [a,b] сетку
a=x0<x1<x2<…<xn-1<xn=b (5.1)
а соответствующие им значения функции f:
yi = f ( xi ), i=0, 1, 2, …, n (5.2)
представляют собой сеточную функцию. Такой способ задания функции называется табличным.
Задача аппроксимации заключается в следующем: по сеточной функции (5.1),(5.2) построить функцию непрерывного аргумента g ( x ), аппроксимирующую функцию f ( x ): g ( x ) » f ( x ).
Это позволит приближенно вычислять функцию f ( x ) в любой точке отрезка [ a , b ], а не только в точках сетки (5.1).
Интерполирование.
Пусть дана система функций j 0 ( x ), j 1 ( x ), …, j n ( x ), определенная на отрезке [a,b]. Для этой системы ищется аппроксимирующая функция g ( x ) в виде линейной комбинации функций:
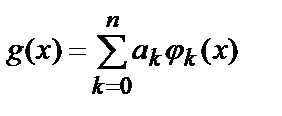(5.3)
Требование: в точках сетки (5.1) функция g (х) должна принимать такие же значения (5.2), что и функция f ( x ):
g ( xi )= f ( xi ) (5.4)
Сформулированную таким образом задачу построения функции непрерывного аргумента g ( x ), аппроксимирующей функцию f ( x ), называют задачей интерполирования.
Наиболее часто рассматривают интерполирование полиномами, тогда:
j 0 ( x )=1, j 1 ( x )= x , …, j n ( x )= xn . (5.5)
В этом случае функция g ( x ) записывается как полином n-ой степени:
g(x)=Pn(x)=a0+a1x+a2x2+…+anxn. (5.6)
Существует несколько форм его записи, одна из них принадлежит Лагранжу:
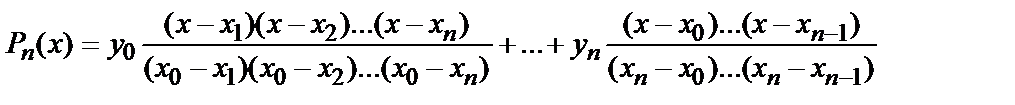(5.7)
При этом условие (4.6) выполняется во всех точках сетки:
Pn ( xi )= yi , i =0, 1, 2,…, n (5.8)
Пример 5.1. Построить интерполяционный полином для функции y=sin(x). Сетка состоит из трех точек: x0 = 0, x1 = π/6, x2 = π/2. Сеточная функция имеет вид: y0 = 0, y1 = 1/2, y2 = 1.
Решение:
Поскольку максимальный индекс точек сетки равен 2, то и степень интерполяционного полинома будет равна двум. Используя формулу Лагранжа (4.7), получится:
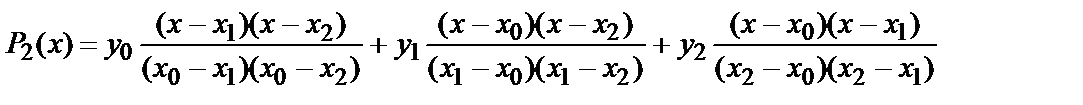
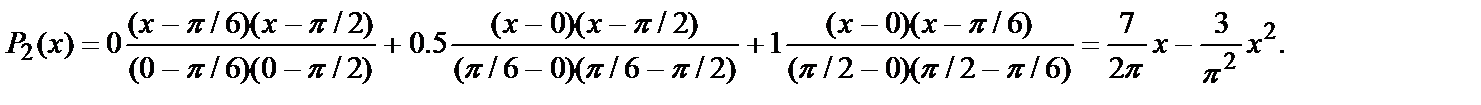
Легко проверить, что в точках сетки этот полином Р2(х) принимает нужные значения.
Для определения погрешности интерполирования можно рассчитать значение sin(x) и P2(x) в точке х= π/4:
e=sin(π/4) – P2(π/4) = 0.7071 – 0.6875 = 0.02
Значительная величина погрешности определяется тем, что на отрезке длиной π/2, взята грубая сетка, состоящая всего из трех точек.
Метод наименьших квадратов.
А) аппроксимация полиномами.
В методе наименьших квадратов аппроксимирующая функция y(x) ищется в виде суммы, аналогичной (5.3), но содержащей сравнительно небольшое число слагаемых:
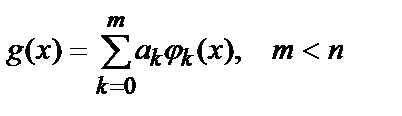(5.9)
Предполагая, что каким-то образом выбраны коэффициенты ak, тогда в каждой точке сетки (451) можно вычислить погрешность:
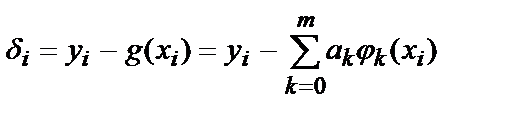(5.10)
Функция δ, принимающая значения δ1, δ2, …, δn, представляет собой сеточную функцию и называется погрешностью решения .
Сумма квадратов этих величин называется суммарной квадратичной погрешностью:
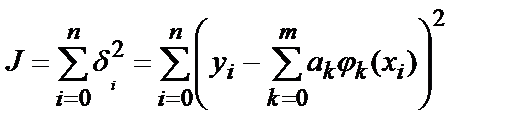(5.11)
Возникает задача: найти такой набор коэффициентов ak , при которых суммарная квадратичная погрешность J оказывается минимальной.
Функцию (5.9) с набором коэффициентов, удовлетворяющих этому требованию, называют наилучшим приближением по наименьших квадратов.
Построение наилучшего приближения сводится к задаче поиска экстремума функции J от нескольких переменных:
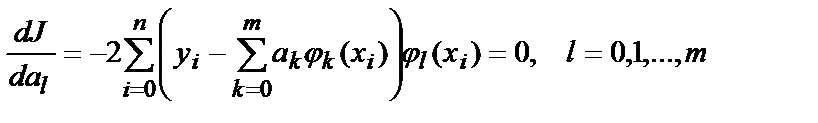(5.12)
Уравнения (4.12) можно переписать в виде:
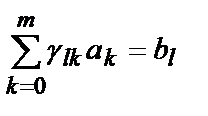, l=0,1,…,m (5.13)
где
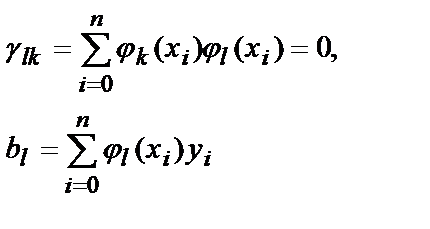(5.14)
Таким образом, получена система линейных алгебраических уравнений (5.14), в которой роль неизвестных играют искомые коэффициенты разложения a0, a1, … , am.
Пример 5.2. Пусть известны экспериментальные значения концентрации некоторого вещества M в зависимости от времени протекания реакции:
Таблица 1.
| t, min | M, моль/л |
| 30 | 1,526 |
| 40 | 1,341 |
| 50 | 1,195 |
| 60 | 0,962 |
| 70 | 0,871 |
Считая, что концентрация вещества описывается полиномом второй степени, определить его коэффициенты.
Решение:
Здесь общее количество точек равно 5, степень полинома m =2, j 0 (х)=1, j 1 (х)=х, j 2 (х)=х2.
Для нахождения коэффициентов полинома, необходимо решить систему линейных уравнений. Определим ее коэффициенты:
, 
, 
, 
, 
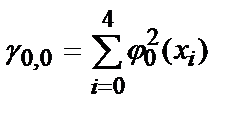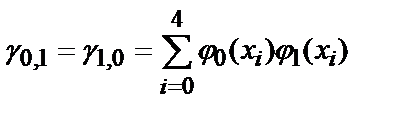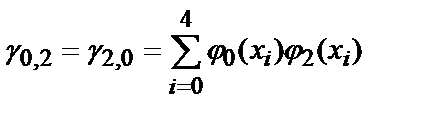
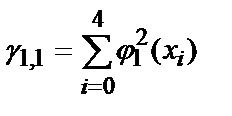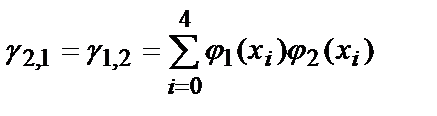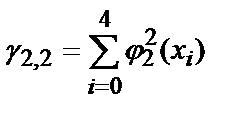
g 0,0 =5, g 0,1 =250, g 0,2 =13 ¢ 500, g 1,1 =13 ¢ 500, g 1,2 =775 ¢ 000, g 2,2 =46 ¢ 590 ¢ 000
и коэффициенты, стоящие в правых частях системы:
, 
, 
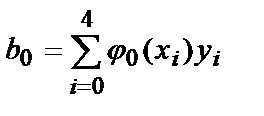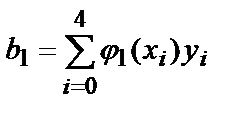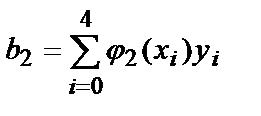
b 0 = 5,895 , b 1 =27 7,86 , b 2 =1423 7,6
Итоговая система для определения коэффициентов имеет вид:
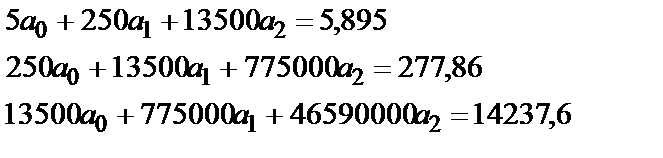
Для решения этой системы можно использовать любые имеющиеся пакеты математических прикладных программ, в том числе можно использовать и написанную программу для решения систем линейных алгебраических уравнений, приведенной в теме 2.
Применяя эту программу, можно рассчитать коэффициенты а0, а1, а2.
Окно ввода этой программы будет иметь вид:
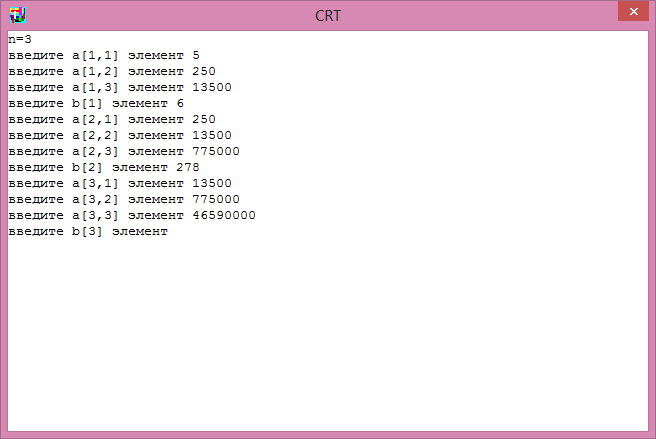
Данные в программу вводятся согласно вышеописанной системе.
После введения данных программа выдает исходную матрицу А и после этого преобразованную матрицу. Поскольку матрица верхнетреугольная, то при выводе второй и третьей строк они немного смещены влево относительно первой строки. В правой части каждой строки стоят значения bi.
Значения полученных переменных даны в виде x[1], x[2], x[3].
Следует учитывать, что коэффициент x[1] – это коэффициент, стоящий при х2, т.е. а2 ; коэффициент х[2] это коэффициент, стоящий при х, т.е. а1; а x[3] – это коэффициент, стоящий без х, т.е. а0..
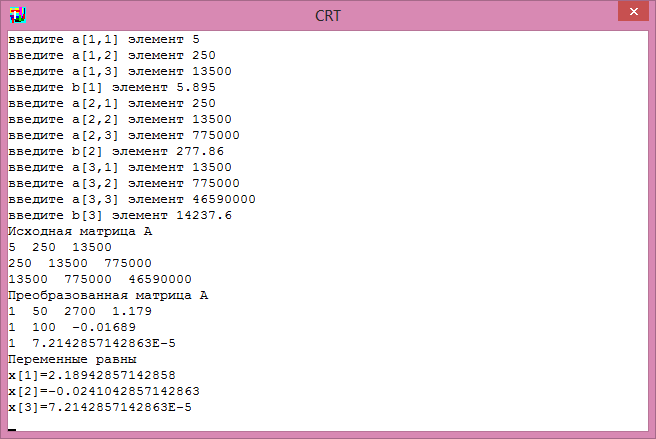
Зная эти значения, можно выписать уравнение квадратичной функции, аппроксимирующей экспериментальные данные:
Р2(х) = 7 × 10-5 x2 - 0,024 x + 2,19 (5.15)
Экспериментальные и расчетные значения показаны в таблице:
| t, min | M, моль/л | P2 |
| 30 | 1,526 | 1,531229 |
| 40 | 1,341 | 1,340686 |
| 50 | 1,195 | 1,164571 |
| 60 | 0,962 | 1,002886 |
| 70 | 0,871 | 0,855629 |
Рассчитаем суммарную квадратичную погрешность замены экспериментальных значений функцией вида (4.15):
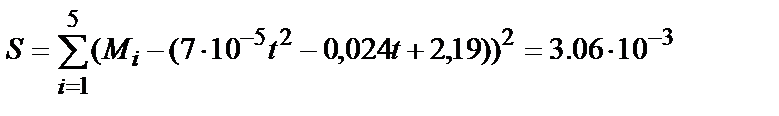
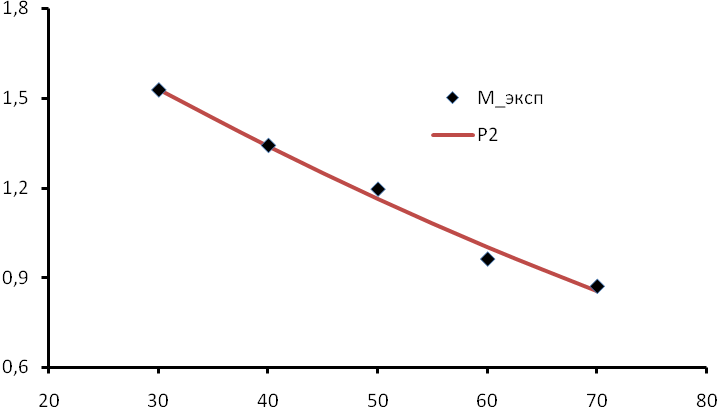
Таким образом, найденная зависимость, описываемая уравнением (5.15), имеет достаточно хорошую согласованность с эмпирически полученными значениями М., что видно по следующему рисунку:
Б) аппроксимация методом выравнивания (линеаризация).
Очень часто вид эмпирической зависимости подсказывает исследователю, какой именно аналитической функцией ее можно описать. Но, зачастую, количество параметров, от которых зависит выбранная аналитическая функция больше двух. Для их определения необходимо применять методы оптимизации, которые дадут значения параметров с некоторой погрешностью.
Однако, если выбранная аналитическая зависимость характеризуется лишь двумя параметрами, то можно использования метод выравнивания. Лишь после этого можно перейти к отысканию тех значений постоянных коэффициентов, которые дадут наилучшее приближение экспериментальных и расчетных величин.
Метод выравнивания заключается в преобразовании функции y=j(x) таким образом, чтобы превратить ее в линейную функцию. Достигается это путем замены переменных х и y новыми переменными:
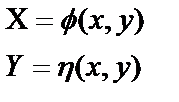(5.16)
которые выбираются так, чтобы получилось уравнение прямой:
Y = A + BX (5.17)
Числовые значения коэффициентов А и В определяются как:
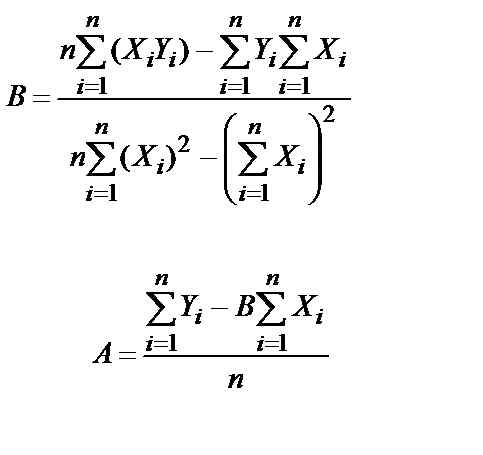(5.18)
Пример 5.3. Изменение концентрации вещества M в реакции подчиняется экспоненциальному закону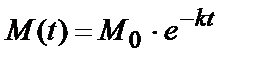 
. Необходимо определить начальное значение вещества M 0 и значение константы скорости расхода вещества k .
Решение:
Для того, чтобы превратить исходную экспоненциальную зависимость в линейную, необходимо ее прологарифмировать. Тогда получим:
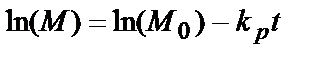(5.19)
Вводя новые переменные: Y = ln ( M ), A = ln ( M 0 ), B = –- kP, X = t
cоставим дополнительную таблицу (помимо таблицы 1) для расчета коэффициентов линейной зависимости Y(X):
Таблица 2.
| X | Y | XY | X2 |
| 30 | 0.423 | 12.678 | 900 |
| 40 | 0.293 | 11.736 | 1600 |
| 50 | 0.178 | 8.905 | 2500 |
| 60 | -0.039 | -2.322 | 3600 |
| 70 | -0.138 | -9.667 | 4900 |
| 250 | 0.717 | 21.330 | 13500 |
В последней строке таблицы приведены суммы величин.
Подставляя требуемые значения в формулу (4.18), рассчитаем коэффициенты линейной зависимости:
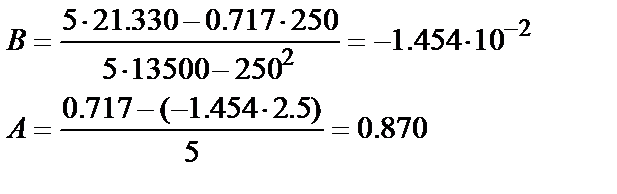
Отсюда, kP =1.45 × 10-2, М0 = е0.87 = 2.39.
Следовательно, экспоненциальное уравнение, описывающее изменение концентрации вещества M в реакции имеет вид:
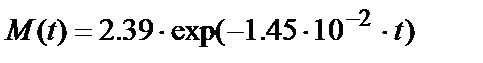(5.20)
Таблица данных, содержащая экспериментальные значения М и расчетную зависимость приведена ниже:
| t, min | M_расч | М_расч |
| 30 | 1,526 | 1,546963 |
| 40 | 1,341 | 1,338157 |
| 50 | 1,195 | 1,157536 |
| 60 | 0,962 | 1,001294 |
| 70 | 0,871 | 0,866142 |
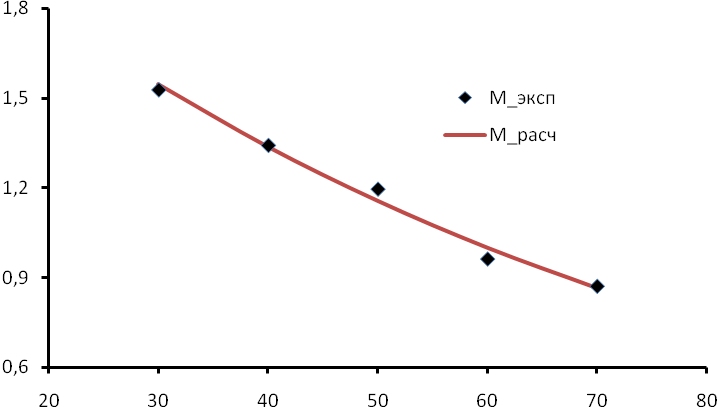
Таблица проиллюстрирована на следующем рисунке:
Рассчитаем суммарную квадратичную погрешность замены экспериментальных значений функцией вида (5.20):
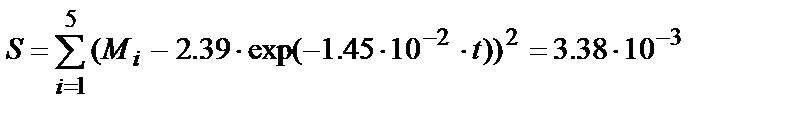
Таким образом, найденная зависимость, описываемая уравнением (5.20), имеет также достаточно хорошую согласованность с эмпирически полученными значениями М.
В) Сравнение методов
Проанализируем полученные в пунктах А) и Б) значения. Для этого достаточно сравнить эти значения между собой.
Сравнение можно провести путем поиска наименьшего среди суммарных отклонений функции.
В данном случае наилучшее приближение дает описание экспериментальной кривой полиномом второго порядка. Квадратичная погрешность замены экспериментальных значений функциональной зависимостью равна:
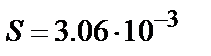
Это означает, что полином второго порядка лучше приближен к экспериментальным точкам, чем экспоненциальная зависимость. Хотя, экспоненциальная зависимость дает возможность определять недостающие кинетические параметры: начальную концентрацию и константу скорости реакции.
Поэтому, при решении задачи аппроксимации выбор аппроксимирующей функции следует делать, исходя из требований и условий задачи.
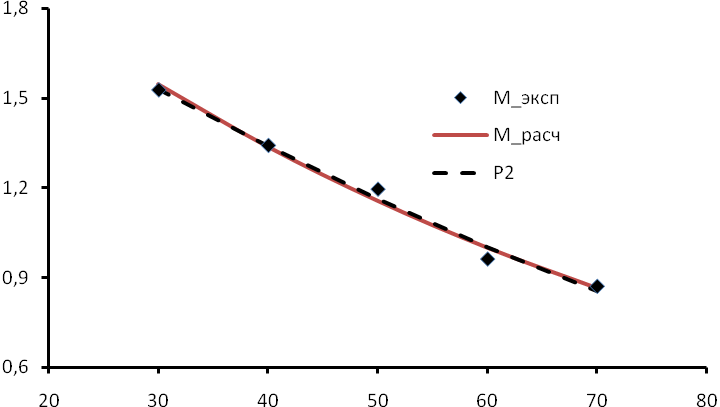
Как видно по рисунку, сравнение «на глаз» невозможно, поскольку графики расчетных зависимотей сливаются между собой, поэтому единственно допустимым способом выбора вида аппроксимирующей функции остается поиск наименьшей суммарной квадратичной погрешности.
Вообще говоря, некоторые пакеты прикладных программ имеют в своем арсенале готовые модули, позволяющие подбирать для экспериментальной зависимости аналитические функции различного вида.
Выбор той или иной аппроксимирующей функции пользователь делает сам, а на экран выдается коэффициент корреляции.
Дата: 2019-03-05, просмотров: 261.
