Пусть рассматривается некий процесс, зависящий от одного параметра х и описываемый функцией y = f ( x ). Поставим задачу: определить такие значения параметра х, равные х*, которые вызывают остановку процесса, то есть выполнение условия:
f ( x )=0 (4.1)
Теорема о существовании нуля непрерывной функции : Если функция f ( x ) непрерывна на отрезке [ a , b ] и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения (3.1).
Пусть известно, что на [ a , b ] существует единственный корень уравнения (1). Потребуем, чтобы функция:
1) была непрерывна на [ a , b ] вместе со своими производными f ¢ ( x ) и f ² ( x );
2) в точках a и b функция имеет разные знаки, т.е. f ( a ) × f ( b )<0;
3) производные f ¢ ( x ), f ² ( x ) – сохраняют знак на всем [ a , b ], т.е. функция должна быть строго монотонной на [ a , b ].
Метод бисекции (половинного деления). Суть метода: [ a , b ] делится на два равных отрезка [ a , c ] и [ c , b ]. Рассчитывается значение функции в точке с. Если f ( c ) ¹ 0, то из двух отрезков [ a , c ] и [ c , b ] выбирается тот, в котором функция f ( x ) имеет разные знаки на концах и обозначается за [ a 1 , b 1 ]. Отрезок [ a 1 , b 1 ] разбивается на два равных отрезка точкой с1.Считается значение f(c1). Если оно не равно нулю, то из двух отрезков [ a 1 , c 1 ] и [ c 1 , b 1 ] выбирается тот, в котором функция f ( x ) имеет разные знаки на концах и обозначается за [ a 2 , b 2 ]. Продолжая аналогичные действия, в результате строится последовательность отрезков [ an , bn ]. На n-ом шаге процесса получаем:
an £ х* £ bn. (4.2)
Это двойное неравенство показывает, что число an определяет х* с недостатком, а число bn – с избытком. За решение уравнения (4.1) принимается значение x*=(an + bn)/2 при условии, что
Dn < e (4.3)
где Dn = |bn – an|, а e - заданная точность.
Очевидно, что скорость сходимости метода половинного деления будет равна ½.
Метод итераций. Предположим, что уравнение (3.1) можно переписать в виде:
x = j ( x ) (4.4)
Возьмем произвольное значение х0 из области определения функции j(x) и будем строить последовательность чисел {xn}, определенных с помощью рекуррентной формулы
xn +1 = j ( xn ), n =0, 1, 2, … (4.5)
Последовательность {xn} называется итерационной последовательностью.
Точность найденного решения определяется формулой (4.3):
Dn = |xn – xn-1| < e (4.6)
где e - заданная точность.
Метод хорд. Будем полагать, что функция f ( x ) дважды дифференцируема на [ a , b ] функция.
| f(a) × f ² (а) >0 |
| a |
| х 1 |
| х 2 |
| b |
Метод хорд требует, чтобы один конец отрезка [a,b], был неподвижен. Условие неподвижности точки:
f ”( x н ) × f ( x н ) > 0 (4.7)
Расчетная формула для определения n-ого приближения:
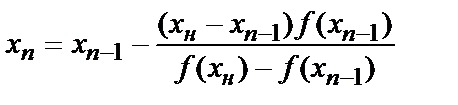(4.8)
При выполнении условия (4.6) за решение принимается х*= xn .
Метод касательных (метод Ньютона). Будем полагать, что функция f ( x ) – это дважды дифференцируемая на [ a , b ] функция.
Метод заключается в следующем: из точки, для которой выполняется условие (4.7) испускается касательная к кривой y = f ( x ), которая пересекает ее в точке х1 – эта точка станет первым приближением к корню х*, затем вновь проводим касательную к кривой в точке (х1, f ( x 1 )) – получим х2 и т.д.
|
| Формула определения абсцисс точек пересечения касательных с осью Ох имеет вид:
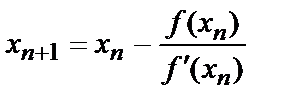 (4.9)
Точка xn будет являться корнем уравнения (4.1) при выполнении (4.6).
Геометрическое представление метода показано на рисунке:
|
Комбинированный метод хорд и касательных. Для ускорения сходимости используют комбинированный метод хорд и касательных. Здесь одновременно из точки ( b , f ( b )) проводят касательную, а из точки ( a , f ( a )) – хорду. Получается новый интервал ( a 1 , b 1 ) и процедура повторяется до выполнения условия
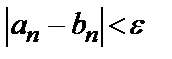(4.10)
В это)м случае за «истинное» решение уравнения (4.1) можно принять значение
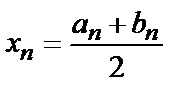(4. 11)
Пример 4.1.
Найти решение уравнения f(x)=x-cos(x)=0 на отрезке [0,1] с ε=0, 01 с помощью каждого описанного метода.
Решение:
Для этой функции на указанном отрезке выполняются следующие условия:
f’>0, f’’>0.
Следующая таблица показывает работу метода половинного деления:
Метод половинного деления
а=
0
b=
1
ε=
0,01
№ ит
А
c
b
Знак
(f(a))
Знак
(f(c))
Знак
(f(b))
Δ
0
0
0,5
1
-
-
+
1
1
0,5
0,75
1
-
+
+
0,5
2
0,5
0,625
0,75
-
-
+
0,25
3
0,625
0,688
0,75
-
-
+
0,125
4
0,688
0,719
0,75
-
-
+
0,0625
5
0,719
0,734
0,75
-
-
+
0,03125
6
0,734
0,742
0,75
-
+
+
0,015625
7
0,734
0,738
0,742
-
-
+
0,007813
8
0,738
0,740
0,742
-
+
+
0,003906
Как видно из таблицы на 7 -ой итерации получен корень уравнения х=0,738. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Замечание. Для метода половинного деления всегда можно определить количество требуемых итераций по формуле:
n > log2 ((b-a)/e)
где n – ближайшее большее целое число.
Следовательно, для нашей задачи: n > log2 ((1-0)/0.01) = log2100 = 6.64 , то есть n=7, что и видно из таблицы.
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0.5,1]+ É -[0.5,0.75]+ É -[0.625,0.75]+ É -[0.688,0.75]+ É -[0.719,0.75]+ É -[0.734,0.75]+ É -[0.734,0.742]+ É 0.738
Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
Метод итераций.
Метод итераций
а=
0
b=
1
ε=
0,01
№
х
φ(x)
Δ
0
0,5
0,877583
0,5
>
0,01
1
0,877583
0,639012
0,377583
>
0,01
2
0,639012
0,802685
0,23857
>
0,01
3
0,802685
0,694778
0,163673
>
0,01
4
0,694778
0,768196
0,107907
>
0,01
5
0,768196
0,719165
0,073418
>
0,01
6
0,719165
0,752356
0,04903
>
0,01
7
0,752356
0,730081
0,03319
>
0,01
8
0,730081
0,74512
0,022275
>
0,01
9
0,74512
0,735006
0,015039
>
0,01
10
0,735006
0,741827
0,010114
>
0,01
11
0,741827
0,737236
0,00682
<
0,01
12
0,737236
0,74033
0,004591
<
0,01
Как видно из таблицы на 11 -ой итерации получен корень уравнения х=0,742. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Замечание. Для нулевой итерации за х0 взяли среднее значение между a и b, равное 0,5.
Метод хорд. Определим неподвижную точку, для этого проверим условие (4.7) в точках a и b:
f ”(а) × f (а) < 0, f ”( b ) × f ( b ) > 0
Значит, неподвижной точкой является точка b.
Таблица по работе метода хорд имеет вид:
|
Метод хорд | |||||
| а= | 0 | b= | 1 | ε= | 0,01 |
| х_неп=1, f(x_неп)= 0,459698 | х0=0 | ||||
| № | X |
F(x) | Δ | ||
| 0 | 0 | -1 | 1 | > | 0,01 |
| 1 | 0,685 | -0,0893 | 0,685073 | > | 0,01 |
| 2 | 0,736 | -0,00466 | 0,051226 | > | 0,01 |
| 3 |
0,739 | -0,00023 |
0,002646 | < |
0,01 |
| 4 | 0,739 | -1,2E-05 | 0,000133 | < | 0,01 |
Как видно из таблицы на 3 -ей итерации получен корень уравнения x=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0.685,1]+ É -[0.736,1]+ É -[0.739,1]+ É 0.739
Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
Метод касательных.
Метод касательных
а=
0
b=
1
ε=
0,01
№
Х
F(x)
F'(x)
Δ
0
0,5
-0,37758
1,479426
1
>
0,01
1
0,755
0,027103
1,685451
0,255222
>
0,01
2
0,739
9,46E-05
1,673654
0,016081
>
0,01
3
0,739
E-09
1,673612
E-05
<
0,01
4
0,739
0
1,673612
7,06E-10
<
0,01
Как видно из таблицы на 3 -ей итерации получен корень уравнения x=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0,755]+ É -[0,0.739]+ É -[0,0.739]+ É 0.739.
Верхние индекс, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
Дата: 2019-03-05, просмотров: 258.
