Математическое моделирование систем и процессов

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Математическое моделирование систем и процессов

Практикум

по выполнению контрольной работы для студентов заочной формы обучения специальности

23.05.05 «Системы обеспечения движения поездов»

Красноярск

2018

УДК 519.6

ББК 22.19

Белобородова Татьяна Викторовна. Математическое моделирование систем и процессов: Практикум по выполнению контрольной работы для студентов заочной формы обучения специальности 23.05.05 «Системы обеспечения движения поездов» / Т.В. Белобородова, П.В. Новиков. – КрИЖТ ИрГУПС. – Красноярск, 2018. - 35 с.

Практикум разработан на основе рабочей программы дисциплины «Математическое моделирование систем и процессов» для студентов заочной формы обучения специальности 23.05.05 «Системы обеспечения движения поездов». Практикум содержит теоретический материал, задание и примеры выполнения контрольной работы по дисциплине.

Издается по решению Методического совета КрИЖТ ИрГУПС.

СОДЕРЖАНИЕ

Введение. 4

Требования к содержанию и оформлению контрольной работы.. 4

1. Задание на контрольную работу. 5

Задача 1. Решение нелинейного уравнения. 5

Задача 2. Решение систем линейных алгебраических уравнений. 5

Задача 3. Вычисление определенных интегралов. 6

Задача 4. Решение дифференциальных уравнений. 6

Задача 5. Задачи регрессии. 7

2. Численные методы решения задач. 8

2.1. Решение нелинейных уравнений. 8

2.1.1. Постановка задачи. 8

2.1.2. Метод Ньютона. 9

2.2. Решение систем линейных алгебраических уравнений. 12

2.2.1. Постановка задачи. 12

2.2.2. Методы исключения. 13

2.3. Численные методы интегрирования. Квадратурные формулы.. 16

2.3.1. Постановка задачи. 16

2.3.2. Формула Симпсона. 17

2.4. Решение задачи Коши для обыкновенных дифференциальных уравнений 19

2.4.1. Постановка задачи. 19

2.4.2. Метод Рунге-Кутта. 20

2.5. Методы обработки числовых данных. 21

3. Реализация численных методов в среде MathCad или SMath Studio. 26

3.1. Решение нелинейных уравнений. 26

3.2. Решение систем линейных алгебраических уравнений. 27

3.3. Вычисление определенных интегралов. 29

3.4. Решение задач Коши для обыкновенных дифференциальных уравнений с начальными условиями. 30

3.5. Нахождение уравнения линейной регрессии. 33

Заключение. 34

Библиографический список. 35

Введение

Основная задача данного практикума – помочь студентам-заочникам в выполнении контрольной и лабораторных работ, а также в подготовке к зачету. В практикуме даны пояснения к выполнению лабораторных работ, варианты заданий, общие методологические правила выполнения контрольной работы.

Студентам при выполнении контрольной и лабораторных работ нужно:

· решить нелинейное равнение;

· решить систему линейных алгебраических уравнений;

· вычислить определенный интеграл;

· решить дифференциальное уравнение;

· решить задачу регрессии.

Все необходимые сведения для решения задач в контрольной работе и выполнения лабораторных работ, даны в п. 2 и п. 3 данных указаний.

Требования к содержанию и оформлению контрольной работы

Контрольная работа выполняется на листах формата А4 с соблюдением требований Положения «Требования к текстовой и графической документации. Нормоконтроль» [10]:

Контрольная работа включает следующие части:

· титульный лист;

· решенные задания. Каждое задание должно содержать:

1 условие задачи,

2 решение задачи, проведенное без помощи программных пакетов по примерам, приведенным в п. 2 практикума. Решение записывается от руки;

3 решение задачи с помощью программного пакета SMathStudio или MathCAD, по примерам, приведенным в п. 3 практикума. Решение распечатывается в виде одного или нескольких скриншотов программного пакета;

· список использованных источников.

Вариант контрольной работы выбирается по последней цифре студенческого билета.

Список литературы, который является заключительной частью контрольной работы, должен содержать не менее пяти литературных источников.

Работа выполняется и сдается в соответствии с «Инструкцией по выполнению, сдаче, регистрации, проверке, хранению контрольных и курсовых работ (проектов) студентов заочной формы обучения» в установленные учебным процессом сроки.

Задание на контрольную работу

Данная контрольная работа содержит 5 задач. Вариант каждой задачи выбирается в соответствии с личным учебным шифром (номером зачетной книжки).

Задача 5. Задачи регрессии

Методом наименьших квадратов построить линейную функцию для табличных данных (табл. 5). Нарисовать график полученной функции и показать исходные данные.

Таблица 5

Значения x	-4	-3	-2	-1	0	1	2	3	4	5
Вариант	Значения y
1.	-3,32	-3,64	-3,57	3,54	2,75	4,02	5,24	5,79	7,48	13,49
2.	-3,51	-1,68	1,1	-2,2	3,81	4,79	2,51	5,7	8,84	11,72
3.	-4,66	-3,5	0,7	-2,39	-0,06	2,47	5,74	4,83	6,18	8,51
4.	-7,49	-4,4	-0,28	-0,82	-1,15	4,38	7,26	7,31	7,92	9,6
5.	-3,25	-2,07	-2,23	-1,24	4,9	2,92	8,25	5,15	6,53	11,23
6.	-5,35	-1,5	-0,86	0,27	0,49	3,63	7,78	6,27	8,33	13,07
7.	-2,36	-5,62	-3,53	-1,64	-0,66	5,24	7,89	7,87	7,83	10,96
8.	-5,44	-1,57	-0,23	-0,46	-0,29	5,86	8,07	5,01	6,28	7,55
9.	-7,13	-1,88	-1,06	-0,17	2_?65	1,2	2,71	6,19	6,59	8,38
10.	-4,94	-2,25	0,67	-1,57	2,49	2,7	6,26	5,88	9,44	10,1

Постановка задачи

Требуется найти такие значения аргумента x, для которых справедливо уравнение

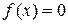(1)
где функция 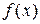дифференцируема. При этом уравнение (1) может быть алгебраическим или трансцендентным*.

Корень x уравнения (1) геометрически представляет собой абсциссу точки пересечения (рис. 1а), точки касания (рис. 1б) или другой общей точки (рис. 1в) графика функции 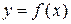и оси х.

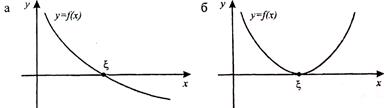
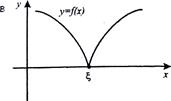
Рис. 1

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни уравнения (1) в виде некоторого конечного соотношения (формулы). Примером такого решения является нахождение корней квадратного уравнения, известного из школьного курса алгебры.

В дальнейшем будут рассматриваться только уравнения, которые, как правило, не имеют аналитических формул для вычисления корней уравнения. Для них приходится пользоваться итерационными методами нахождения решения, которые состоят из двух этапов:

1. Отыскание приближенного значения корня (отделение корня), т.е. нахождение такого конечного промежутка, внутри которого имеется единственное решение данного уравнения (1). Отделение корней можно осуществить аналитическим (находя критические точки функции) и графическим (путем построения графика функции) способами.

Для отделения корней применяют следующий критерий: если на отрезке [a; b] функция 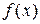непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то этот отрезок содержит один и только один корень уравнения (1). Достаточным признаком монотонности функции 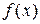на некотором отрезке является сохранение знака ее производной на этом отрезке (если 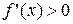, то функция возрастает; если 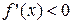, функция убывает).

2. Уточнение приближенного значения до некоторой заданной степени точности.

В практических задачах решением называют любое значение аргумента x отличающееся по модулю от точного значения корня x не более чем на малую величину e.

В общем случае итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, ..., х_к, ... Если эти значения с ростом k стремятся к истинному значению корня

,
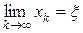то говорят, что итерационный процесс сходится.

Метод Ньютона

В основе метода Ньютона (метода касательных) лежит разложение функции f(x) в ряд Тейлора:

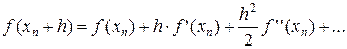
Члены, содержащие h во второй и более высоких степенях, отбрасываются, используется соотношение 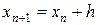и предполагается, что 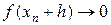при 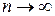. Отсюда получается итерационная формула

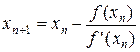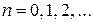, (2)

Графическое представление метода показано на рис. 2. В точке (х₀, f(х₀)) проводят касательную к графику функции f(x) и точку пересечения ее с осью х принимают за новое приближение x₁. Для него строят новую касательную, находят точку х₂ и т.д. до тех пор, пока значение 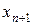не станет достаточно близко к корню x.

Счет прекращается, когда выполняется условие

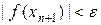. (3)

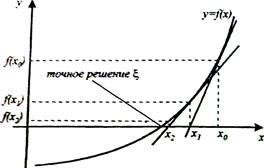
Рис. 2

Метод Ньютона обладает квадратичной скоростью сходимости для .достаточно гладких функций f(x). Быстрота его сходимости в большой степени зависит от выбора начального приближения х₀. Метод обеспечивает быструю сходимость, если выполняется неравенство

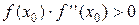, (4)
поэтому чаще всего в качестве начального приближения выбирают тот конец интервала [а; b], на котором знаки f и f ’’ совпадают (условие Фурье).

Достоинством этого метода является его быстрая сходимость, а недостатком то, что помимо 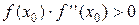надо вычислять и 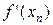, поэтому метод применим, если вычисление производной f ' не сложнее, чем вычисление функции f.

Пример 2.1. Найти корень уравнения

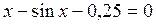(5)

с точностью e = 0,001 методом Ньютона.

Решение

1. Обозначим левую часть уравнения как функцию .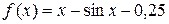

2. Вычислим первую и вторую производные:

,
.

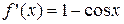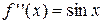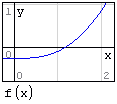3. Построим график функции и определим по нему отрезок, на котором функция пересекает ось x. В данном примере на графике видим, что f(x) обращается в нуль на отрезке от 0 до 2. Отрезок следует выбрать так, чтобы на нем было только одно пересечение f(x) с осью x.

4. Проверим выполнение условия Фурье ( 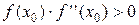) на границах заданного интервала [0;2].

Подставляем левую границу интервала :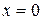

,
.

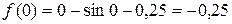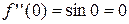Произведение 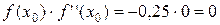, т.е. условие Фурье не выполняется.

Подставляем правую границу интервала :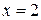

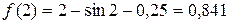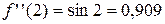Произведение 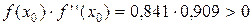, т.е. условие Фурье выполняется. Поэтому за начальное приближение 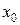принимаем правую границу интервала: .

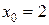5. Первая итерация. Найдем уточненное значение :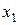

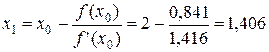Найдем модуль функции для значения :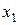

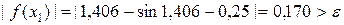Поскольку условие 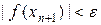не выполняется, то делаем следующую итерацию.

6. Вторая итерация. Найдем уточненное значение :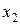

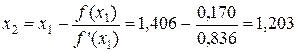Найдем модуль функции для значения :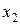

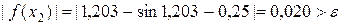Поскольку условие 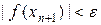не выполняется, то делаем следующую итерацию.

7. Третья итерация. Найдем уточненное значение :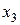

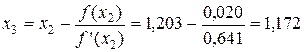Найдем модуль функции для значения :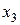

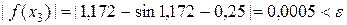Условие 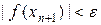выполняется, решение найдено с заданной точностью.

8. Ответ: На отрезке 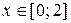корень уравнения 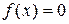равен х = 1,172 с точностью e = 0,001.

Постановка задачи

В общем случае система линейных алгебраических уравнений
имеет вид

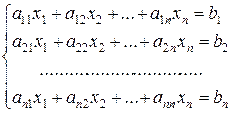(6)

Требуется найти неизвестные 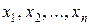, удовлетворяющие системе уравнений (6).

В матричной форме СЛАУ (6) записывается в виде

,
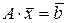где

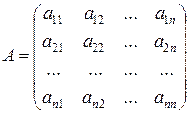; - вещественная матрица данной системы (6);

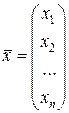; - вектор неизвестных;

; - вектор свободных членов.

Матрица А системы (6) является квадратной. Определитель
матрицы

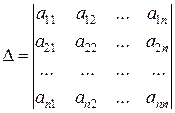
называется определителем системы.

Необходимым и достаточным условием того, что система (6) имеет единственное решение, является условие, что ее определитель д не равен нулю. Если D = 0, то решений может быть или бесконечное множество, если уравнения системы линейно зависимы, или не существовать ни одного, если уравнения противоречивы.

Эффективность способов решения СЛАУ во многом зависит от структуры и свойств матрицы А: размерности я, обусловленности, симметричности, заполненности (т.е. соотношения между числом нулевых и ненулевых элементов), специфики расположения ненулевых элементов в матрице и др.

Все существующие численные методы решения СЛАУ делятся на прямые и итерационные. Прямые методы дают точное решение задачи за конечное число операций, если все они выполняются без погрешностей округления. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса линейных систем. К прямым методам относятся методы исключения (Гаусса, Гаусса-Жордана и др.), декомпозиции и др. Итерационные методы позволяют находить приближенное решение СЛАУ путем построения последовательности приближений (итераций), начиная с некоторого начального приближения. К этому классу относятся методы простых итераций, Зейделя и множество других. Их достоинством является то, что они обладают свойством самоисправления ошибок в ходе вычислений. Недостатком является то, что они не всегда сходятся. Алгоритмы решения линейных систем с использованием итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений заранее определить трудно. Чаще всего итерационные методы применяются к большим системам уравнений с разреженными или слабозаполненными матрицами.

Методы исключения

Метод исключения Гаусса основан на приведение системы уравнений (6) к треугольному виду и является одним из наиболее часто используемых прямых методов решения СЛАУ. Процесс решения состоит из двух этапов.

1-й этап – прямой ход – система уравнений приводится к треугольному виду. Для этого на первом шаге из всех уравнений кроме первого, исключается неизвестное 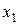. На втором шаге из всех уравнений, кроме первого и второго исключается 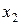и т.д., пока не исключатся неизвестные 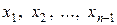. В итоге приходим к новой системе уравнений

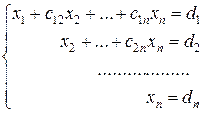(7)

2-й этап – обратный ход. Из полученной системы уравнений (7) последовательно, начиная с последнего уравнения, определяются неизвестные .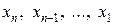

Если главные коэффициенты а_и в системе (б) близки к нулю, то этот метод становится непригоден для нахождения решения. В этом случае применяют метод Гаусса с выбором главного элемента. Он заключается в том, что при прямом ходе производится выбор наибольшего по модулю (главного) элемента в рассматриваемом столбце и соответствующая перестановка строк. Это исключает деление на ноль при исключении неизвестных и повышает точность вычислений при наличии ошибок округления.

Усовершенствованной разновидностью метода Гаусса является метод Гаусса-Жордана. Если в методе Гаусса преобразования затрагивают только уравнения, стоящие под главной диагональю, то в методе Гаусса-Жордана преобразуются также и уравнения, стоящие над главной диагональю. В результате последовательного исключения неизвестных исходная матрица приводится к диагональному виду.

Достоинством этого метода является облегчение получения решения – не нужен обратный ход. Недостатком является увеличение числа операций по сравнению с классическим методом Гаусса.

Алгоритмы исключения неизвестных зарекомендовали себя на практике как эффективные и надежные методы. Тем не менее, и эти алгоритмы могут не привести к решению, если система уравнений плохо обусловлена. Говорят, что линейная система уравнений (6) является плохо обусловленной, если малые изменения элементов матрицы коэффициентов А или правых частей 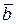приводят к большим изменениям в решении 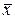. В этом случае ни от какого численного метода нельзя ожидать, что он даст точное решение, а во многих случаях не следует даже и пытаться искать решение.

Пример 2.2. Решить методом Гаусса систему уравнений

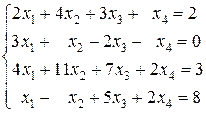(8)

Решение

Прямой ход. 1-й шаг.

Разделим первое уравнение системы (8) на 2:

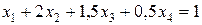, (9)

умножим уравнение (9) на (–3) и сложим со вторым уравнением системы (8):

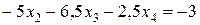Умножим уравнение (9) на (–4) и сложим с третьим уравнением системы (8):

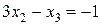Вычтем уравнение (9) из четвертого уравнения исходной системы (8):

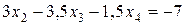В результате всех преобразований получили новую систему уравнений

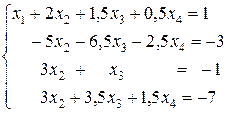(10)

2-й шаг.

Разделим второе уравнение полученной системы (10) на (–5):

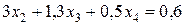. (11)

Умножим уравнение (11) на (–3) и сложим с третьим уравнением системы (10):

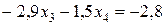Умножим уравнение (11) на (–3) и сложим с четвертым уравнением системы (10):

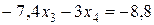В итоге получили систему уравнений

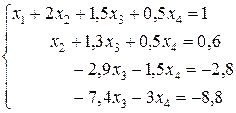(12)

3-й шаг.

Делим третье уравнение полученной системы (12) на (–2,9):

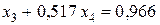. (13)

Умножим уравнение (13) на 7,4 и сложим с третьим уравнением системы (12):

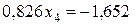В итоге получили систему уравнений

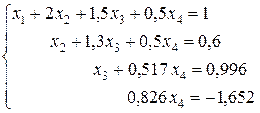
4-й шаг.

Делим четвертое уравнение полученной системы на 0,826:

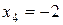В результате всех преобразований получили треугольную систему уравнений

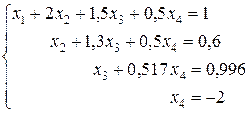
Обратный ход. Из этой системы уравнений последовательно находим

;

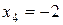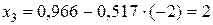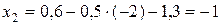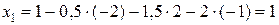Проверка

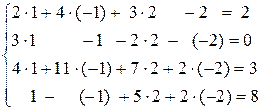
Постановка задачи

Найти значение определенного интеграла

(14)
при условии, что концы отрезка интегрирования а и b конечны, а f(x) является непрерывной, функцией от х на всем интервале a ≤ x ≤ b.

Общий подход к решению данной задачи следующий. Определенный интеграл I представляет собой площадь криволинейной трапеции, ограниченной кривой f(x), осью х и прямыми х = а и х = b. Разбивая интервал [a,b] на множество меньших интервалов, можно приближенно найти площадь каждой полоски, получающейся при таком разбиении, и, суммируя площади этих полосок, получить приближенное значение интеграла. При этом можно рассмотреть два способа разбиения исходного отрезка интегрирования:

Разбиение на интервалы производится заранее, они обычно выбираются равными. Кроме того, если вычисление интеграла предполагается производить «вручную», то интервалы выбираются так, чтобы значения х, соответствующие концам каждого интервала, было как можно легче вычислять. К этой категории методов принадлежат методы прямоугольников, трапеций и Симпсона.

Местоположение и длина интервалов определяются путем анализа: сначала ставится требование достичь наивысшей точности с заданным числом интервалов, а затем в соответствии с этим определяются их границы. Примером такого подхода является метод Гаусса.

Формулы для приближенного вычисления определенного интеграла (14) вида

(15)
называются квадратурными. Постоянные являются коэффициентами (весами) квадратуры, – ее узлами, а правая часть равенства (15) – квадратурной суммой. Чем больше значение n, тем точнее вычисляется интеграл. Все методы различаются значениями узлов и весов . Сравнение эффективности различных методов производится по степени полинома, который данным методом интегрируется точно, без ошибки. Чем выше степень полинома, тем выше точность метода.

2.3.2. Формула Симпсона

Разобьем отрезок интегрирования на 2n равных частей длиной ; при этом , , , (рис. 3).

Через каждую тройку точек

проведем параболу.

Рис.3

В результате получим n криволинейных трапеций, ограниченных сверху параболами. На каждом отрезке заменим площадь под кривой f(x) на площадь такой трапеции и просуммируем их:

Можно доказать, что для каждой трапеции справедлива формула

Тогда

(16)

Эта формула называется формулой Симпсона. В ней все ординаты с четными номерами (кроме нулевой и последней) имеют коэффициент 2, а с нечетными - 4. Формула (16) точна для полиномов третьего порядка.

Абсолютная погрешность формулы (16) оценивается неравенством

Пример 2.3. Вычислить определенный интеграл

методом Симпсона. Отрезок интегрирования разбить на 10 частей.

Решение

Разбиваем отрезок интегрирования [а; b] на 10 частей. При этом . Шаг интегрирования . Подынтегральная функция . Узлы интегрирования вычисляют по формуле

, , , .

Для удобства сведем вычисление узлов интегрирования и значений функции в них в таблицу (табл. 6).

Таблица 6

Номер узла
0	1	3·1 + ln 1 = 3
1	1 + 0,1 = 1,1	3·1,1 + ln 1,1 = 3,395
2	1,1 + 0,1 = 1,2	3·1,2 + ln 1,2 = 3,782
3	1,2 + 0,1 = 1,3	3·1,3 + ln 1,3 = 4,162
4	1,3 + 0,1 = 1,4	3·1,4 + ln 1,4 = 4,534
5	1,4 + 0,1 = 1,5	3·1,5 + ln 1,5 = 4,905
6	1,5 + 0,1 = 1,6	3·1,6 + ln 1,6 = 5,27
7	1,6 + 0,1 = 1,7	3·1,7 + ln 1,7 = 5,631
8	1,7 + 0,1 = 1,8	3·1,8 + ln 1,8 = 5,988
9	1,8 + 0,1 = 1,9	3·1,9 + ln 1,9 = 6,342
10	1,9 + 0,1 = 2	3·2 + ln 2 = 6,693

По формуле Симпсона (16) имеем

Постановка задачи

Рассмотрим задачу Коши для дифференциального уравнения 1-го порядка

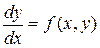(17)

с начальным условием

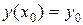. (18)

Требуется найти функцию 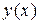, удовлетворяющую уравнению (17) и начальному условию (18).

Хотя решение некоторых задач Коши может быть найдено аналитически, во многих случаях, в том числе для большинства задач, представляющих практический интерес, такой путь часто оказывается невозможным, например, коэффициенты или функции в дифференциальном уравнении могут содержать нелинейности или задаваться в виде таблиц экспериментальных данных. В этом случае пользуются приближенным методам решения задач Коши.

Выделяют два класса приближенных методов решения задач (17), (18): одношаговые и многошаговые. Первый класс методов требует для нахождения следующего значения неизвестной функции 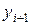значение только в одной текущей точке 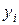, т.е.

,
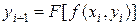а второй класс – в нескольких, например,

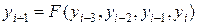Методы второго класса поэтому не обладают свойством «самостартования», т.е. ими нельзя начать решение задачи Коши, оно всегда начинается одношаговыми методами. К достоинствам многошаговых методов относят в основном меньший объем памяти компьютера, требующейся для их реализации, и возможность теоретической оценки погрешности решения. Представителем класса многошаговых методов являются методы прогноза и коррекции. К классу одношаговых методов относятся методы Эйлера, Рунге-Кута и др. Как и во многих других случаях, эти два класса методов лучше сочетать, учитывая их достоинства и недостатки.

Метод Рунге-Кутта

Идея метода Рунге-Кутта состоит в представлении разности

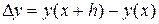
в виде суммы поправок 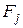с коэффициентами :

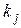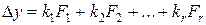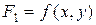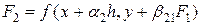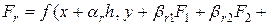
где , , …, 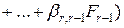. Коэффициенты 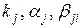находятся сравнением разложения 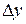и 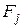, по степеням h.

В сущности, этот метод объединяет целое семейство методов решения дифференциальных уравнений первого порядка (метод Эйлера, модифицированный метод Эйлера и др.). Наиболее распространенным из них является метод четвертого порядка точности для r = 4, ошибка при этом имеет порядок. Этот метод часто и называют методом Рунге-Кутта. Расчеты в нем проводятся по формулам

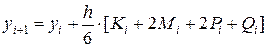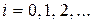, (19)
где

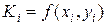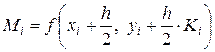, , (19a)

, .

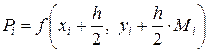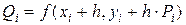Пример 2.4. Решить уравнение

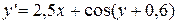
с начальным условием

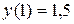
на отрезке [1; 3] с шагом .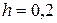

Решение

Имеем 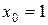, 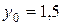. Используя формулу (19) для нахождения значений K_i, M_i, P_i, Q_i получим значения 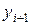. Для удобства сведем все вычисления в таблицу (табл. 7).

Таблица 7


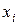
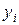
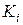
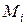
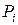
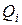
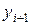
1	1,5	1,995	2,084	2,077	2,19	1,917
1,2	1,917	2,189	2,331	2,326	2,513	2,384
1,4	2,384	2,512	2,754	2,757	3,077	2,938
1,6	2,938	3,078	3,488	3,515	4,046	3,642
1,8	3,642	4,047	4,684	4,748	5,461	4,588
2	4,588	5,458	6,103	6,135	6,491	5,802
2,2	5,802	6,493	6,469	6,471	6,157	7,086
2,4	7,086	6,167	5,816	5,848	5,658	8,258
2,6	8,258	5,656	5,75	5,75	6,165	9,419
2,8	9,419	6,171	6,898	6,967	7,905	10,813
3	10,813

Решение

Сведем все вычисления, необходимые для составления
нормальной системы уравнений (21), в таблицу (табл. 9).

Таблица 9


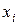
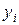
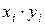
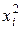
	–2	0,5	–1	4
	0	1	0	0
	1	1,5	1,5	1
	2	2	4	4
	4	3	12	16
Σ	5	8	16,5	25

Тогда система нормальных уравнений (21) имеет вид

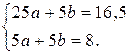
Отсюда

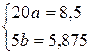
или

; .

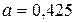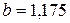Получаем зависимость

y = 0,425х + 1,175.

Для сравнения полученной зависимости и исходных данных

можно составить таблицу

Таблица 10

x	–2	0	1	2	4
y	0,5	1	1,5	2	3
0,425x+1,175	0,325	1,175	1,6	2,025	2,875
δ	–0,175	0,175	0,1	0,025	–0,125

Также для сравнения можно построить график, где исходные данные отобразить точками, а полученную зависимость – линией (рис. 6).

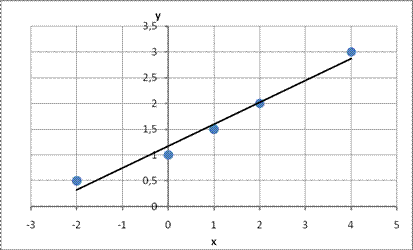
Рис. 6

MathCAD

Для решения одного нелинейного уравнения с одной неизвестной система MathCAD имеет встроенную функцию, которая в зависимости от типа задачи может иметь или два или четыре аргумента и, соответственно, работает несколько по-разному: root(f(x),x); root(f(x),x,a,b), где f(x) - скалярная функция, определяющая исходное нелинейное уравнение (4.1); х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которопй происходит поиск корня.

Первый тип функции root требует предварительного задания начального приближения х₀ переменной х. Поиск корня будет производиться вблизи этого значения методом секущих. Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума функции f(x). В этом случае секущая будет иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого корня. Аналогичные проблемы могут возникнуть, если начальное приближение выбрано слишком далеко от настоящего решения, или f(x) имеет особенность типа бесконечности.

Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого заведомо находится корень. В этом случае следует использовать функцию root с четырьмя аргументами; присваивать начальное значение переменной х в этом случае не нужно. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента).

Решение (распечатка MathCAD)
f(x) := x – sin(x) – 0.25 x := 0,0.1..2 х := 1 – начальное приближение s := root(f(x), x) s =1.171 - корень уравнения f(s)=–4.836´10^–5 - погрешность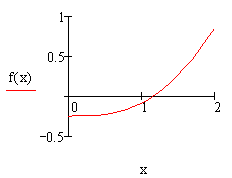

SMath Studio

Для решения одного нелинейного уравнения с одной неизвестной система SMath Studio имеет встроенную функцию, которая в зависимости от типа задачи может иметь или два или три аргумента: roots(f(x); x) или roots(f(x); x; a), где f(x) – скалярная функция, определяющая исходное нелинейное уравнение (4.1); х – скалярная переменная, относительно которой решается уравнение; а – начальное приближение переменной х.

Решение (распечатка SMath Studio)

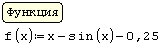
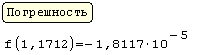
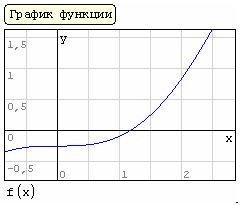
MathCAD

Для решения систем уравнений в среде MathCAD можно применять вычислительный блок Given/Find. Он состоит из трех частей:

1. ключевое слово Given;

2. система уравнений, записанная с помощью логических операторов;

3. вызов встроенной функции Find(xl, х2,..., хп).

Перед применением блока Given/Find необходимо задать начальные значения переменным xl, x2,хп.

Однако более наглядным является решение СЛАУ в матричной форме. В этом случае используется встроенная функция lsolve(A,b), где А - матрица коэффициентов системы, b - вектор правых частей.

Решение (распечатка MathCAD)

Решение с помощью вычислительного блока Given/Find	Решение с помощью встроенной функции lsolve
xl :=1 х2:=1 х3:= 1 х4:=1 Given 2·xl + 4·х2 – 3·хЗ + х4 = 2 3·xl + х2 – 2·хЗ - х4 = 0 4·xl +11·х2 + 7·х3 + 2·х4 = 3 xl – x2 + 5·x3+2·x4 = 8 y := Find(xl ,х2,хЗ,х4)

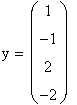
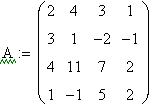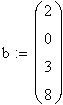
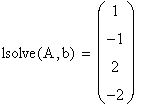
SMath Studio

Для решения систем уравнений в среде SMath Studio применяется матричный метод решения: коэффициенты левых частей уравнений записываются в квадратную матрицу A размером 4´4, свободные коэффициенты записываются в столбец B размером 4´1. Решением будет столбец X, который находится умножением обратной матрицы на столбец B: 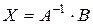. Решение существует, если определитель матрицы A не равен нулю. Получив решение, нужно сделать проверку, т.е. убедиться, что .

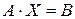Решение (распечатка SMath Studio)

MathCAD

Интегрирование в MathCAD может быть аналитическим или численным. В случае аналитического интегрирования вводится знак символьного равенства (→). В этом случае будет найдено точное значение интеграла. Конечно, возможно это только для относительно небольшого круга несложных подынтегральных функций.

В случае численного интегрирования после ввода интеграла нужно ввести знак равенства (=). В этом случае будет найдено приближенное значение интеграла одним из встроенных численных методов.

Пользователь в среде MathCAD имеет возможность сам выбрать алгоритм численного интегрирования. Для этого необходимо:

записать вычисляемый интеграл;

щелкнуть правой кнопкой мыши на любой части интеграла;

в появившемся контекстном меню выбрать один |из. четырех численных метода интегрирования:

Romberg (Ромберга) - для большинства функций, не содержащих особенностей;

Adaptive (адаптивный) - для функций, быстро меняющихся на интервале/интегрирования;

Infinite Limit (бесконечный предел) - для интегралов с бесконечными пределами (несобственных);

Singular Endpoint (сингулярность на конце) - модифицированный алгоритм Ромберга для функций, не определенных на одном или обоих концах отрезка интегрирования.

В большинстве случаев MathCAD сам выбирает численный метод. Для этого в том же контекстном меню устанавливается флажок AutoSelect (автоматический выбор). Если подынтегральная функция «хорошая», т.е. не меняется на интервале интегрирования слишком быстро и не обращается на нем в бесконечность, то чаще всего применяется алгоритм Ромберга.

Решение (распечатка MathCAD)

Аналитическое вычисление интеграла

Численное вычисление интеграла

- использован адаптивный метод

SMath Studio

Интегрирование в SMath Studio может быть только численным. Сначала нужно задать функцию f(x) и пределы интегрирования. Затем с панели Функции вставить шаблон определенного интеграла, заполнить его и нажать знак равенства (=). В этом случае будет найдено приближенное значение интеграла встроенным численным методом. Для наглядности на графике отобразить функцию f(x) и область интегрирования с помощью матрицы ab.

Решение (распечатка SMath Studio)

Пределы интегрирования

Примечание1: границы области интегрирования вставляются как матрица 4 ´ 2, затем матрица заполняется как на рисунке.

Примечание2: под график нужно сначала вставить алгебраическую систему с панели «Функции», затем в нее вписать f(x) и ab

MathCAD

При решении задач Коши для обыкновенных дифференциальных уравнении методом Рунге-Кутта с переменным шагом в MathCAD пользуются вычислительным блоком Given/Odesolve. Он состоит из трех частей:

1. ключевое слово Given;

2. уравнение и начальные условия, записанные с помощью логических операторов;

3. вызов встроенной функции Odesolve(x, x1) дадя. решения, уравнения на интервале (x0,x1).

Допустимо задание функции в виде Odesolve(x, x1, step), где step-, внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге-Кутта будет вычислять решение. Чем больше step, тем с лучшей точностью будет получен результат, нотем больше времени будет затрачено на его поиск. Подбором этого параметра можно в несколько раз ускорить расчеты без существенного ухудшения точности решения.

Решение (распечатка MathCAD)

Решение в среде MathCAD с помощью функции rkfixed методом Рунге-Кутта четвёртого порядка:

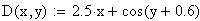
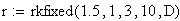
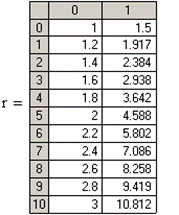
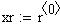
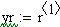
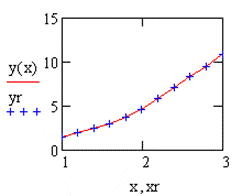
Решение в среде MathCAD с помощью функции Odesolve:

Given

у' (х) = 2.5 -х + cos(y (х) + 0.6)

у(1)=1.5

y:=Odesolve(x,3)

SMath Studio

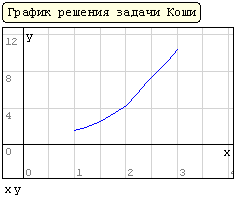
При решении задач Коши для обыкновенных дифференциальных уравнений методом Рунге-Кутта с фиксированным шагом в SMath Studio используется функция rkfixed. Правая часть дифференциального уравнения записывается как функция D(x;y). Кроме этого, задаются: шаг, границы интервала решения, начальное значение функции y(x) на левой границе интервала, и вычисляется количество точек на интервале.

Решение (распечатка SMath Studio)

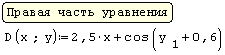
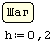Границы интервала

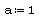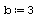
Примечание: Если в правой части сама функция y встречается внутри функций sin, cos, tg, ln и т.п., ее нужно написать с индексом 1 (единица), т.е. вместо y должно быть написано y ₁. Это можно сделать с помощью шаблона

«Элемент вектора» с панели Матрицы.

Начальное значение функции

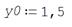
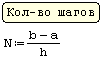
Примечание: Для выполнения задания необходимо, чтобы в SMathStudio было установлено дополнение «ODE Solvers». Наличие дополнения можно проверить в менеджере расширений SMathStudio, открыв его через главное меню программы: Сервис – Дополнения… . Если дополнение отсутствует, его можно установить при наличии подключения к Интернету, сменив «Локальное хранилище» на «Галерею онлайн» в окне менеджера расширений.

MathCAD

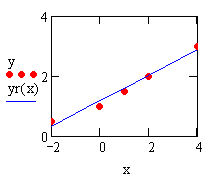
Для реализации линейной регрессии в системе MathCAD имеется функция line(x,y), которая выдает вектор из двух элементов (а, b) линейной регрессии a+b х; где x – вектор значений аргумента; у – вектор значений функции.

Решение (распечатка MathCAD)

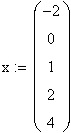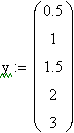
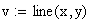
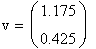
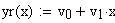
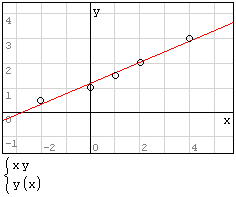
SMath Studio

Для реализации линейной регрессии в системе SMath Studio используются функции Slope и Intercept, которые дают значения коэффициента наклона прямой и сдвига по оси ординат, соответственно. Данные по х и по у нужно задать в виде матриц-столбцов. Кроме того, нужно задать дополнительный столбец из латинских букв "o" в кавычках для наглядного построения данных в виде точек.

Решение (распечатка SMath Studio)

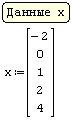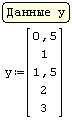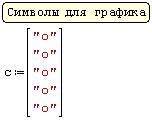
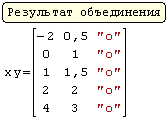
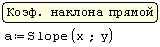
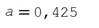
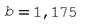
Примечание: Для выполнения задания необходимо, чтобы в SMathStudio было установлено дополнение «Statistical Tools». Как установить дополнение, см. в примечании к предыдущему примеру.

Заключение

Выполнение контрольной работы позволит студентам освоить численные методы решения тех задач, которые встречаются в их профессиональной сфере. Краткая теоретическая часть позволит студентам глубже понять теоретические основы используемых численных методов, а применение пакетов программ сделает решение профессиональных задач более эффективным.

Библиографический список

1 Кирьянов, Д.В. Самоучитель MathCAD 2001 [Текст] : самоучитель / Д. В. Кирьянов.- СПб. : БХВ-Петербург, 2002. - 544 с

2 Бахвалов, Н.С. Численные методы [Текст] : учеб. пособие для ВУЗов / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков.- М. : БИНОМ, 2006. - 636 с.

3 Голубева, Н.В. Математическое моделирование систем и процессов [Текст] : учеб. пособие для ВУЗов ж.-д. трансп. / Н. В. Голубева.- СПб.: Лань, 2013. - 192 с.

4 Белобородова, Т.В. Математическое моделирование в среде MathCAD [Текст] : учебное пособие / Т. В. Белобородова.- Красноярск: КФ ИрГУПС, 2003. - 366 с.

5 Бояркина, Галина Петровна. Математическое моделирование систем и процессов [Электронный ресурс]: учеб. пособие. Часть 1: Численные методы, 2011. - 160 с. on-line

6 Багдуева, Ханда Нимаевна. Математическое моделирование систем и процессов [Электронный ресурс]: учеб. пособие. Часть 2: Моделирование динамических систем, 2011. - 144 с.

7 Менакер, К.В. Математическое моделирование систем и процессов [Электронный ресурс]: методические указания по выполнению контрольной работы для студентов 2 курса заочной формы обучения специальности 23.05.05 "Системы обеспечения движения поездов" всех специализаций / К. В. Менакер, М. А. Павленко.- Чита: ЗабИЖТ, 2014. -15 с.

8 Маничев, В.Б. Численные методы. Достоверное и точное численное решение дифференциальных и алгебраических уравнений в CAE-системах САП [Электронный ресурс]: учебное пособие / В. Б. Маничев, В. В. Глазкова, И. А. Кузьмина.- М.: ИНФРА-М, 2016.

9 Безруков, А.И. Математическое и имитационное моделирование [Электронный ресурс]: учебное пособие / А. И. Безруков, О. Н. Алексенцева.- М. : ФОРУМ : ИНФРА-М, 2017. - 227 с.

10 Положение «Требования к оформлению текстовой и графической документации. Нормоконтроль» [Электронный ресурс]: принято решением Ученого Совета 27.01.2012г., протокол № 6; Утв. приказом ректора 06.03.2012г., № 63 (изд. апрель 2017 г.).- Иркутск: ИрГУПС, 2017. - 46 с.

Практикум по выполнению контрольной работы

Белобородова Татьяна Викторовна

Новиков Павел Вадимович

Математическое моделирование систем и процессов

Практикум

по выполнению контрольной работы для студентов заочной формы обучения специальности

23.05.05 «Системы обеспечения движения поездов»

Красноярск

2018

УДК 519.6

ББК 22.19

Издается по решению Методического совета КрИЖТ ИрГУПС.

СОДЕРЖАНИЕ

Введение. 4

Требования к содержанию и оформлению контрольной работы.. 4

1. Задание на контрольную работу. 5

Задача 1. Решение нелинейного уравнения. 5

Задача 2. Решение систем линейных алгебраических уравнений. 5

Задача 3. Вычисление определенных интегралов. 6

Задача 4. Решение дифференциальных уравнений. 6

Задача 5. Задачи регрессии. 7

2. Численные методы решения задач. 8

2.1. Решение нелинейных уравнений. 8

2.1.1. Постановка задачи. 8

2.1.2. Метод Ньютона. 9

2.2. Решение систем линейных алгебраических уравнений. 12

2.2.1. Постановка задачи. 12

2.2.2. Методы исключения. 13

2.3. Численные методы интегрирования. Квадратурные формулы.. 16

2.3.1. Постановка задачи. 16

2.3.2. Формула Симпсона. 17

2.4. Решение задачи Коши для обыкновенных дифференциальных уравнений 19

2.4.1. Постановка задачи. 19

2.4.2. Метод Рунге-Кутта. 20

2.5. Методы обработки числовых данных. 21

3. Реализация численных методов в среде MathCad или SMath Studio. 26

3.1. Решение нелинейных уравнений. 26

3.2. Решение систем линейных алгебраических уравнений. 27

3.3. Вычисление определенных интегралов. 29

3.4. Решение задач Коши для обыкновенных дифференциальных уравнений с начальными условиями. 30

3.5. Нахождение уравнения линейной регрессии. 33

Заключение. 34

Библиографический список. 35

Введение

Студентам при выполнении контрольной и лабораторных работ нужно:

· решить нелинейное равнение;

· решить систему линейных алгебраических уравнений;

· вычислить определенный интеграл;

· решить дифференциальное уравнение;

· решить задачу регрессии.

Требования к содержанию и оформлению контрольной работы

Контрольная работа включает следующие части:

· титульный лист;

· решенные задания. Каждое задание должно содержать:

1 условие задачи,

· список использованных источников.

Вариант контрольной работы выбирается по последней цифре студенческого билета.

Задание на контрольную работу

Дата: 2019-03-05, просмотров: 349.

12 3 4 5 6 7 8 9 Следующая ⇒