В практике проектирования дискретных вычислительных устройств для минимизации булевых функций «вручную» используют специального вида таблицы, представляющие собой разложение единичного n-мерного куба на плоскости, сохраняющее отношение смежности вершин. Такие таблицы известны для nÎ{3,4-18}. Очевидно, с точки зрения здравого смысла таблицы для больших значений n (скажем, n>8) использовать не целесообразно (лучше написать программу). Для n-местной булевой функции такая таблица должна содержать 2n клеток, в каждую из которых записывается значение функции на том наборе значений переменных, номер которого совпадает с номером клетки. Нумерация клеток сохраняет отношение смежности вершин, так что любые две рядом расположенные клетки являются соседними и могут склеиваться друг с другом. В таблицах также возможно склеивание клеток, расположенных рядом по вертикали и по горизонтали, а также симметрично относительно некоторых осей симметрии таблицы. В склеивании могут участвовать 2k клеток, в которых k каких-либо переменных принимают все возможные наборы значений. Эти k переменных являются свободными переменными интервала, который содержит k свободных и n-k связанных переменных. Интервалу соответствует множество, содержащее 2k вершин единичного n-мерного куба {0,1}n
Процесс минимизации в классе дизъюнктивных нормальных форм (ДНФ) сводится к визуальному отысканию максимальных интервалов функции, покрывающих наибольшее число вершин единичного n-мерного куба. При этом отпадает необходимость в использовании импликантных таблиц.
Диаграммы Вейча
При небольшом числе переменных (n=3,4) для минимизации булевых функций используют диаграммы Вейча.
Для функции трех переменных нумерация клеток диаграммы Вейча приведена на Рис. 1.
| x1 |
| |||||
|
| ||||||
| x2 | 6 | 7 | 3 | 2 | ||
| 4 | 5 | 1 | 0 | |||
|
| ||||||
| x3 |
| |||||
Рисунок 1 Диаграмма Вейча для 3-х переменных
Диаграмма содержит 23=8 клеток. В диаграмме указаны группы по 23-1=4 клеток, в которых каждая из переменных принимает значение 1.
Определим максимальные интервалы и соответствующую МДНФ для функции трех переменных, заданной вектором af=(0111 1011).Изображение этой функции на диаграмме Вейча показано на рис.4 в предположении, что нумерация переменных в последовательности, задающей номер клетки, производится слева направо.
Из рис.4 видно, что множество единиц данной функции покрывается тремя максимальными интервалами, которым соответствует МДНФ = x2 Ú x1`x3 Ú`x1x3.
|
 | |||||
 | |||||
 | |||||
   1 1
| 1 |  1 1
| 1 | ||
| 1 | 0 | 1 | 0 |
|
Обозначенные на рис. 2 максимальные интервалы покрывают множество N1, образуя неприводимое покрытие, которому соответствует МДНФ
f (x1,x2,x3)=x1`x2 Ú x2 Ú`x1x3
Для четырехместной булевой функции таблица содержит 24=16 строк. Соответственно, диаграмма Вейча такой функции содержит 16 клеток, расположение которых показано на Рис. 3, 4. Каждой клетке сопоставлена одна из вершин единичного 4-мерного куба, описанная кортежем 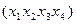 . Двоичные коды кортежей, соответствующие нумерации клеток, приведенной на Рис. 3, представлены на Рис. 4. Из последнего рисунка видно, что каждая переменная принимает значение 1 в 8 клетках таблицы, обозначенных соответствующим указателем.
. Двоичные коды кортежей, соответствующие нумерации клеток, приведенной на Рис. 3, представлены на Рис. 4. Из последнего рисунка видно, что каждая переменная принимает значение 1 в 8 клетках таблицы, обозначенных соответствующим указателем.
| 12 | 13 | 9 | 8 |
| 14 | 15 | 11 | 10 |
| 6 | 7 | 3 | 2 |
| 4 | 5 | 1 | 0 |
|
 | |||
 | |||
| 1100 | 1101 | 1001 | 1000 | ||
| 1110 | 1111 | 1011 |
 1010 1010
| ||
| 0110 | 0111 | 0011 | 0010 | ||
| 0100 | 0101 | 0001 | 0000 |
|
| ||||
| ||||

Примеры минимизации 4-местных булевых функций, заданных векторами a(f)=(1010101010101010) и a(f)=(1001100110011001) приведены на Рис. 5.
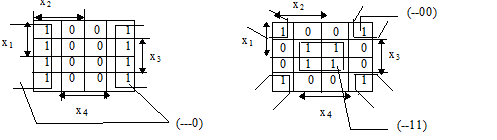
Рисунок 5 Пример определения МДНФ
При дальнейшем увеличении местности булевых функций их минимизация с использованием диаграмм Вейча становится затруднительной из-за громоздкости таблицы и уменьшения ее наглядности. Поэтому при n>4 используют метод симметричных таблиц.
Дата: 2019-03-05, просмотров: 225.