Булевы векторы и единичный n-мерный куб
Вектор  , координаты которого принимают значение в множестве
, координаты которого принимают значение в множестве  , называется двоичным или булевым вектором.
, называется двоичным или булевым вектором.
Множество  называется единичным n-мерным кубом. Упорядоченная последовательность (кортеж) длины n называется вершиной единичного n-мерного куба. Мощность множества вершин единичного n-мерного куба равна
называется единичным n-мерным кубом. Упорядоченная последовательность (кортеж) длины n называется вершиной единичного n-мерного куба. Мощность множества вершин единичного n-мерного куба равна  .
.
На множестве вершин единичного n-мерного куба задаются следующие характеристики:
· Вес вектора или норма вектора, равный  ;
;
· Номер вектора, равный десятичному числу, записанному в двоичной системе счисления:  если разряды двоичного вектора нумеруются справа налево, начиная с 0, т.е.
если разряды двоичного вектора нумеруются справа налево, начиная с 0, т.е.  .
.
· Расстояние Хемминга между двумя булевыми векторами, равное числу разрядов, в которых эти векторы различаются, определяемое как  . Два вектора
. Два вектора  называются соседними, если расстояние Хемминга между ними равно 1, и противоположными, если расстояние Хемминга между ними равно n. Расстояние Хемминга является метрикой, а куб
называются соседними, если расстояние Хемминга между ними равно 1, и противоположными, если расстояние Хемминга между ними равно n. Расстояние Хемминга является метрикой, а куб  - метрическим пространством.
- метрическим пространством.
· На множестве булевых векторов длины n определено отношение предшествования:  . Нетрудно доказать, что отношение предшествования является отношением частичного порядка на множестве вершин единичного n-мерного куба.
. Нетрудно доказать, что отношение предшествования является отношением частичного порядка на множестве вершин единичного n-мерного куба.
· Неупорядоченная пара соседних вершин единичного n-мерного куба называется ребром куба.
· Множество  называется сферой радиуса k с центром
называется сферой радиуса k с центром  .
.
· Множество  называется шаром радиуса k с центром
называется шаром радиуса k с центром  .
.
· Последовательность вершин куба  называется цепью, соединяющей вершины
называется цепью, соединяющей вершины  и
и  , если
, если  . Число k называется длиной цепи.
. Число k называется длиной цепи.
· Множество  называется гранью куба
называется гранью куба  . Множество
. Множество  называется направлением грани, число k – рангом грани, а n- k - размерностью грани. Содержательно грань единичного n-мерного куба – это множество вершин, в которых координаты с индексами
называется направлением грани, число k – рангом грани, а n- k - размерностью грани. Содержательно грань единичного n-мерного куба – это множество вершин, в которых координаты с индексами  принимают одинаковые для всех вершин значения
принимают одинаковые для всех вершин значения  , а все остальные переменные принимают
, а все остальные переменные принимают  возможных наборов значений. Грани ранга k соответствует интервал ранга k. Например, интервал (-01-)={(0010), (0011), (1010), (1011)}. Переменные интервала, которым сопоставляются фиксированные для этого интервала значения из множества {0,1}, называются связанными, переменные, которым сопоставлены другие символы (например, -) называются свободными переменными интервала. Число связанных переменных интервала называется его рангом. Интервалу ранга k соответствует грань размерностью n- k, содержащая
возможных наборов значений. Грани ранга k соответствует интервал ранга k. Например, интервал (-01-)={(0010), (0011), (1010), (1011)}. Переменные интервала, которым сопоставляются фиксированные для этого интервала значения из множества {0,1}, называются связанными, переменные, которым сопоставлены другие символы (например, -) называются свободными переменными интервала. Число связанных переменных интервала называется его рангом. Интервалу ранга k соответствует грань размерностью n- k, содержащая  вершин куба.
вершин куба.
Элементарные булевы функции
Элементарными булевыми функциями называются функции с арностью 0, 1 и 2. При этом нужно заметить, что множество функций двух переменных включает в себя все 0-местные и 1-местные функции, в описании которых присутствует две или одна фиктивная переменная соответственно. Множество всех элементарных булевых функций может быть представлено в виде таблицы, содержащей 4 строки и 16 столбцов. Каждый столбец определяет одну из элементарных булевых функций. Наиболее употребимыми являются двуместные функции: {&,Ú,®,«,Å,ê,¯}, одноместные функции f(x)=x и f(x)=`x, и две 0-местные функции: константа 0 и константа 1, не имеющие ни одной существенной переменной (других таких функций в множестве элементарных булевых функций нет).
Элементарные булевы функции используются для аналитического задания булевых функций произвольной местности формулами. При этом используется принцип суперпозиции функций. Согласно этому принципу формула определяется индуктивно:
· Пропозициональная переменная есть формула.
· Если А и В формулы, то любое слово А·В – формула, если ·Î{&,Ú,®,«,Å,ê,¯}. Слово `А также является формулой.
· Других формул нет.
Для формулы может быть построена таблица истинности, которая является ее интерпретацией. Говорят, что пропозициональная формула задает булеву функцию. Соответственно, булева функция реализует ту формулу, которая задает функцию. Очевидно, формула задает единственную булеву функцию. Обратное не справедливо.
Формулы, определяемые суперпозицией функций, могут преобразовываться как алгебраические выражения с использованием множества аксиом и тождеств. Основными из них являются аксиомы тождественности (идемпотентности), коммутативности, ассоциативности, дистрибутивности, поглощения, закон двойного отрицания, правило де-Моргана. Целью преобразования формул является приведение их к каноническому виду. В теории булевых функций используются канонические представления: дизъюнктивная нормальная форма (ДНФ), конъюнктивная нормальная форма (КНФ), полиномиальная нормальная форма. (ПНФ). Для выполнения преобразований используется правило подстановки, которое формулируется следующим образом: если формула образована суперпозицией функций над некоторым множеством функций, то замена вхождения какой-либо функции на равносильную ей не меняет логическое значение функции. Это можно представить как  , если
, если  с точностью до фиктивных переменных.
с точностью до фиктивных переменных.
Диаграммы Вейча
При небольшом числе переменных (n=3,4) для минимизации булевых функций используют диаграммы Вейча.
Для функции трех переменных нумерация клеток диаграммы Вейча приведена на Рис. 1.
| x1 |
| |||||
|
| ||||||
| x2 | 6 | 7 | 3 | 2 | ||
| 4 | 5 | 1 | 0 | |||
|
| ||||||
| x3 |
| |||||
Рисунок 1 Диаграмма Вейча для 3-х переменных
Диаграмма содержит 23=8 клеток. В диаграмме указаны группы по 23-1=4 клеток, в которых каждая из переменных принимает значение 1.
Определим максимальные интервалы и соответствующую МДНФ для функции трех переменных, заданной вектором af=(0111 1011).Изображение этой функции на диаграмме Вейча показано на рис.4 в предположении, что нумерация переменных в последовательности, задающей номер клетки, производится слева направо.
Из рис.4 видно, что множество единиц данной функции покрывается тремя максимальными интервалами, которым соответствует МДНФ = x2 Ú x1`x3 Ú`x1x3.
|
 | |||||
 | |||||
 | |||||
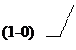   1 1
| 1 |  1 1
| 1 | ||
| 1 | 0 | 1 | 0 |
|
Обозначенные на рис. 2 максимальные интервалы покрывают множество N1, образуя неприводимое покрытие, которому соответствует МДНФ
f (x1,x2,x3)=x1`x2 Ú x2 Ú`x1x3
Для четырехместной булевой функции таблица содержит 24=16 строк. Соответственно, диаграмма Вейча такой функции содержит 16 клеток, расположение которых показано на Рис. 3, 4. Каждой клетке сопоставлена одна из вершин единичного 4-мерного куба, описанная кортежем 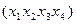 . Двоичные коды кортежей, соответствующие нумерации клеток, приведенной на Рис. 3, представлены на Рис. 4. Из последнего рисунка видно, что каждая переменная принимает значение 1 в 8 клетках таблицы, обозначенных соответствующим указателем.
. Двоичные коды кортежей, соответствующие нумерации клеток, приведенной на Рис. 3, представлены на Рис. 4. Из последнего рисунка видно, что каждая переменная принимает значение 1 в 8 клетках таблицы, обозначенных соответствующим указателем.
| 12 | 13 | 9 | 8 |
| 14 | 15 | 11 | 10 |
| 6 | 7 | 3 | 2 |
| 4 | 5 | 1 | 0 |
|
 | |||
 | |||
| 1100 | 1101 | 1001 | 1000 | ||
| 1110 | 1111 | 1011 |
 1010 1010
| ||
| 0110 | 0111 | 0011 | 0010 | ||
| 0100 | 0101 | 0001 | 0000 |
|
| ||||
| ||||

Примеры минимизации 4-местных булевых функций, заданных векторами a(f)=(1010101010101010) и a(f)=(1001100110011001) приведены на Рис. 5.
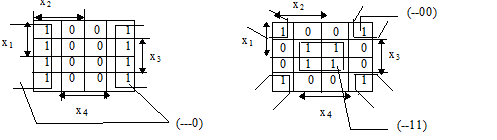
Рисунок 5 Пример определения МДНФ
При дальнейшем увеличении местности булевых функций их минимизация с использованием диаграмм Вейча становится затруднительной из-за громоздкости таблицы и уменьшения ее наглядности. Поэтому при n>4 используют метод симметричных таблиц.
Метод таблиц различий
Метод таблиц различий применяется для минимизации слабо определенных функций произвольной арности, заданных множествами N1 и N0. В отличие от метода симметричных таблиц этот метод является алгоритмизируемым, т.е. можно построить программу минимизации булевых функций. Как и в случае метода Квайна, результатом работы рассматриваемого метода является множество максимальных интервалов функции. Для построения МДНФ потребуется построение импликантной таблицы.
Число строк таблицы различий равно числу единичных интервалов минимизируемой функции. Число столбцов таблицы равно числу нулевых интервалов функции. В ячейках левого столбца таблицы различий, начиная со второй строки, записывают транспонированный вектор, обозначающий один из единичных интервалов функции. В ячейках верхней строки таблицы различий записывают (начиная со второго столбца слева) значения разрядов нулевых интервалов функции.
Векторы, обозначающие интервалы N1 и N0, определяют значения вершин единичного n-мерного куба кортежами вида (xn, xn-1,…,x2,x1), где переменные xi принимают значения в множестве {0,1,-}. Каждая из строк таблицы различий содержит n подстрок, соответствующих индексам переменных в обозначении интервала, Таблица 2. На пересечении i-й строки и j-го столбца записывают вектор, значения разрядов которого определяются применением к одноименным разрядам единичного и нулевого интервалов модифицированной операции суммы по модулю 2, представленной Табл. 1.
Таблица 1 Модифицированная сумма mod2
| x0 x1 | 0 | 1 | - |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| - | 0 | 0 | 0 |
Единица в столбце таблицы различий означает, что значение соответствующей переменной в нулевом и единичном интервалах различны. Следовательно, данная переменная может войти в максимальный интервал данной функции с тем значением, которое эта переменная принимает в множестве N1. Если какой-либо столбец таблицы содержит более одной единицы, это означает, что в обозначение максимального интервала может войти любая из переменных, соответствующих этим единицам, со значением, равным значению этой переменной в единичном интервале.
Таблица 2 Применение метода таблиц различий
|
| Интервалы нулевой области | Допустимые импликанты | |||
| Имена переменных | Интервалы единичной области | 1-10- | 1-001 | 0-100 | |
| x5 x4 x3 x2 x1 | - 0 - 1 0 | 0 0 0 1 0 | 0 0 0 1 1 | 0 0 0 1 0 | 
|
| x5 x4 x3 x2 x1 | 1 0 - 1 1 | 0 0 0 1 0 | 0 0 0 1 0 | 1 0 0 1 1 | 
|
| x5 x4 x3 x2 x1 | 0 - 1 0 1 | 1 0 0 0 0 | 1 0 1 0 0 | 0 0 0 0 1 | 
|
В последнем (правом) столбце таблицы различий записывают формулу вида КНФ, длина которой равна числу нулевых интервалов, и каждый дизъюнкт в которой определяется множеством переменных, отмеченных единицами в каждом столбце данной строки таблицы. Полученную КНФ затем преобразуют к ДНФ. Каждая элементарная конъюнкция, полученная при этом, определяет один из допустимых простых импликантов функции.
Когда все строки таблицы обработаны и получены все допустимые простые импликанты функции, с помощью импликантной таблицы определяют все неприводимые покрытия данной функции с последующим выбором среди них тех, которые имеют минимальный суммарный ранг.
Если среди полученных неприводимых покрытий имеется более одного покрытия с минимальным суммарным рангом, это означает, что данная функция имеет такое же число МДНФ.
Рассмотрим пример минимизации частично определенной функции методом таблиц различий. Пусть 5-местная частично определенная функция задана указанием множеств единичных и нулевых вершин:


В последнем столбце Табл.2 перечислены все претенденты на роль простых импликант. Им соответствуют максимальные интервалы функции.
Для определения МДНФ построим импликантную таблицу, в которой столбцы будут именоваться именами единичных интервалов, которыми задана функция, а строки – именами максимальных интервалов, соответствующих простым импликантам, полученным в Табл. 2. На пересечении i-й строки и j-го столбца импликантной таблицы записывают 1, если j-й единичный интервал является подмножеством i-го максимального интервала, и прочерк в противном случае, Табл 3.
Таблица 3 Импликантная таблица
| N1 Imax | (-0-10) | (10-11) | (0-101) |
| (---1-) | 1 | 1 | - |
| (0---1) | - | - | 1 |
Каждый столбец Табл. 3 содержит по одной единице. Следовательно, найденное множество максимальных интервалов образует покрытие множества N1. Все интервалы являются обязательными. Следовательно, оба импликанта, соответствующие этим максимальным интервалам, должны войти в единственную МДНФ. Таким образом, решением данной задачи является
МДНФ=  .
.
Класс монотонных функций М
 тогда и только тогда, когда на наборах значений переменных, находящихся в отношении предшествования, значения функции находятся в отношении £:
тогда и только тогда, когда на наборах значений переменных, находящихся в отношении предшествования, значения функции находятся в отношении £:

Два булевых вектора  и
и  находятся в отношении предшествования тогда и только тогда, когда одноименные координаты этих векторов находятся в отношении £:
находятся в отношении предшествования тогда и только тогда, когда одноименные координаты этих векторов находятся в отношении £:  . например, в случае трех переменных наборы их значений имеют номера от 0 до 7. Соответственно отношение предшествования на этих наборах определяется так:
. например, в случае трех переменных наборы их значений имеют номера от 0 до 7. Соответственно отношение предшествования на этих наборах определяется так: 
Отношение предшествования на множестве Bn при n³2 является частичным порядком. Мажоритарная функция  в соответствии с определением является монотонной, а трехместная функция XOR – нет,
в соответствии с определением является монотонной, а трехместная функция XOR – нет,  .
.
Множество всех монотонных функций определим как 
Теорема. Класс М замкнут и неполон, т.е. [M]=M¹P2.
ª Так как тождественная функция монотонна, для доказательства замкнутости достаточно показать, что суперпозиция монотонных функций монотонна. Пусть ФÎP2(m), fiÎP2(n), i=1,2,…,m. Докажем, что 
Возьмем два произвольных набора значений переменных таких, что  Тогда
Тогда

и, следовательно,

А так как  то монотонность
то монотонность  доказана, а значит, доказана и замкнутость класса М. Неполнота М следует из существования немонотонных функций. ¨
доказана, а значит, доказана и замкнутость класса М. Неполнота М следует из существования немонотонных функций. ¨
Лемма о немонотонной функции: из произвольной немонотонной функции с помощью подстановки констант и отождествления переменных можно получить функцию отрицания.
ª Пусть  Это означает, что существуют такие наборы значений переменных, находящихся в отношении предшествования, что
Это означает, что существуют такие наборы значений переменных, находящихся в отношении предшествования, что  а
а  Последнее означает, что
Последнее означает, что  Из того, что значения функции на выбранных наборах не равны, следует, что сами наборы также не равны. Пусть расстояние Хемминга между наборами равно 1 и обусловлено различием значений переменной
Из того, что значения функции на выбранных наборах не равны, следует, что сами наборы также не равны. Пусть расстояние Хемминга между наборами равно 1 и обусловлено различием значений переменной  Образуем функцию
Образуем функцию  Тогда
Тогда  Так как функция не монотонна, то
Так как функция не монотонна, то
 .
.
Соотношение  определяет одноместную функцию отрицания.
определяет одноместную функцию отрицания.
Если  , то следует найти в множестве промежуточных наборов два таких соседних набора, на которых происходит нарушение монотонности. После этого задача сводится к предыдущему примеру.
, то следует найти в множестве промежуточных наборов два таких соседних набора, на которых происходит нарушение монотонности. После этого задача сводится к предыдущему примеру.
Пример применения леммы о немонотонной функции. Рассмотрим элементарную булеву функцию ®, вектор значений которой имеет вид:  . Это двуместная функция, нулевой набор предшествует второму, расстояние Хемминга между ними равно 1 по первой переменной и
. Это двуместная функция, нулевой набор предшествует второму, расстояние Хемминга между ними равно 1 по первой переменной и  . Вторая переменная в обоих наборах равна 0, а первая принимает оба возможных значения (мелькает). «Работа» леммы над этой функцией представлена ниже:
. Вторая переменная в обоих наборах равна 0, а первая принимает оба возможных значения (мелькает). «Работа» леммы над этой функцией представлена ниже:
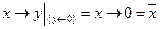 .
.
В соответствии с леммой из немонотонной функции получена одноместная функция отрицания.
¨
Класс линейных функций L
Произвольная булева функция может быть представлена полиномом по mod2 в виде суммы по mod2 монотонных конъюнкций (полинома Жегалкина). Пусть  Говорят, что функция f линейна, если ее полином Жегалкина не содержит конъюнкций, ранг которых превышает 1 и имеет вид
Говорят, что функция f линейна, если ее полином Жегалкина не содержит конъюнкций, ранг которых превышает 1 и имеет вид
 где коэффициенты
где коэффициенты  . Такая функция называется симметрической.
. Такая функция называется симметрической.
Множество всех линейных функций обозначается 

Терема. Класс L замкнут и неполон, т.е. [L]=L¹P2.
ª Так как тождественная функция линейна, то для доказательства замкнутости класса L достаточно показать, что суперпозиция линейных функций есть линейная функция. Доказывается записью соответствующей суперпозиции. Неполнота L следует из существования нелинейных функций. ¨
Очевидно, что мощность класса n-местных линейных функций равна |L(n)|=2n+1.
Лемма о нелинейной функции. Из произвольной нелинейной функции с помощью подстановки констант, тождественной функции и функции отрицания и, возможно, навешиванием отрицания на всю функцию, можно получить конъюнкцию и дизъюнкцию.
Пусть  . Тогда ее полином по mod2 содержит монотонные элементарные конъюнкции ранга выше 1. Выберем среди этих элементарных конъюнкций конъюнкцию минимального ранга (>=2). Для удобства рассуждений положим, что выбранная конъюнкция содержит переменные x1 и x2. Выполним следующие подстановки: всем переменным, участвующим в выбранной конъюнкции, кроме переменных x1 и x2, присвоим значение1. А всем переменным, не вошедшим в выбранную конъюнкцию, присвоим значение 0. В силу единственности полинома, представляющего данную функцию, после выполнения равносильных преобразований полином примет вид:
. Тогда ее полином по mod2 содержит монотонные элементарные конъюнкции ранга выше 1. Выберем среди этих элементарных конъюнкций конъюнкцию минимального ранга (>=2). Для удобства рассуждений положим, что выбранная конъюнкция содержит переменные x1 и x2. Выполним следующие подстановки: всем переменным, участвующим в выбранной конъюнкции, кроме переменных x1 и x2, присвоим значение1. А всем переменным, не вошедшим в выбранную конъюнкцию, присвоим значение 0. В силу единственности полинома, представляющего данную функцию, после выполнения равносильных преобразований полином примет вид:
 .
.
Полином содержит три коэффициента (  ) . Каждому набору значений коэффициентов соответствует своя собственная функция. Следовательно, таких функций будет восемь. Для определения всех функций, порождаемых нелинейной функцией заданного вида, построим таблицу.
) . Каждому набору значений коэффициентов соответствует своя собственная функция. Следовательно, таких функций будет восемь. Для определения всех функций, порождаемых нелинейной функцией заданного вида, построим таблицу.
| a0 a1 a2 | Полином | Функция |
| 000 | x1x2 | F(x1x2)=x1x2 |
| 001 | x2Åx1x2= 
| 
|
| 010 | 
| 
|
| 011 | 
| 
|
| 100 | 
| 
|
| 101 | 
| 
|
| 110 | 
| 
|
| 111 | 
| 

|
Доказано, что из нелинейной функции могут быть получены конъюнкция и дизъюнкция.
Теорема Поста
Теорема. Чтобы множество DÍP2 было функционально полным в P2, необходимо и достаточно, чтобы среди функций этого множества нашлась хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна не самодвойственная функция, хотя бы одна немонотонная и хотя бы одна нелинейная функции.
Следствие 1. В любом функционально полном в Р2 множестве существует функционально полное подмножество, состоящее не более, чем из пяти функций.
Следствие 2. В любом функционально полном множестве существует функционально полное подмножество, состоящее не более чем из четырех функций.
Для доказательства функциональной полноты системы булевых функций по критерию Поста необходимо построить таблицу Поста, строки которой именуются функциями исследуемой системы, а столбцам присваиваются имена предполных классов. На пересечении i-й строки и j-го столбца таблицы ставится 1, если i-я функция принадлежит j-му классу, и 0 – в противном случае. Система функций полна, если в каждом столбце таблицы имеется хотя бы один 0. В противном случае система не является функционально полной в Р2, так как входит целиком в один из предполных классов.
Пусть имеется система функций D={(x1Å x2Åx3 ), (x1®x2), (x1&`x2) , 1}. Таблица Поста для нее будет иметь вид:
| T0 | T1 | S | M | L | |
| f1={(x1Å x2Åx3 ) | 1 | 1 | 1 | 0 | 1 |
| f2=(x1®x2) | 0 | 1 | 0 | 0 | 0 |
| f3=(x1&`x2) | 1 | 0 | 0 | 0 | 0 |
| f4=1 | 0 | 1 | 0 | 1 | 1 |
Согласно критерию Поста система функций D функционально полна, так как в каждом столбце имеется хотя бы один 0. Критерии вхождения функции в предполные классы описаны выше.
Другой вопрос, связанный с использованием теоремы Поста, состоит в определении минимально необходимого набора функций из множества D, образующих функционально полную систему. Система функций D ÍР2 называется базисом в Р2, если она функционально полна в Р2, но при исключении из нее любой функции, она перестает быть функционально полной, т.е. [D]=P2, и "f:((fÎD)®([D\{f}]ÌP2)). Для определения базиса, соответствующего данной системе D, используют метод Петрика, состоящий в следующем. Рассматривая функции системы D как переменные, строим из них конъюнктивную нормальную форму, содержащую пять (по числу предполных классов) элементарных дизъюнкций, включая в каждую элементарную дизъюнкцию только те функции системы, которые принадлежат данному предполному классу, и соединяя полученные дизъюнкции связкой &. Затем преобразуем полученное выражение к ДНФ, использую аксиомы и тождества логики высказываний. Каждая из конъюнкций в полученной ДНФ содержит все функции, образующие базис. Длина ДНФ соответствует числу базисов, соответствующих данной системе. Для рассмотренного примера применение метода Петрика состоит в следующем:
(f2Úf4)&f3&(f2Úf3Úf4)&(f1Úf2Úf3)&(f2Úf3)=(f2Úf4)&f3=f2f3 Ú f3f4.
Таким образом, данная система содержит два базиса: D1= {f2,f3 }, D2={f3, f4}.
Теорема Поста позволяет также определить, можно ли из данного множества булевых функций получить некоторую функцию методом суперпозиций. Рассмотрим, например, можно ли получить симметрическую функцию трех переменных суперпозициями над мажоритарной функцией трех переменных. Построив таблицу Поста, убедимся в невозможности этого, так как m(x3) сохраняет 0, 1, самодвойственная, монотонная и нелинейная, а симметрическая трехместная функция сохраняет 0, 1, самодвойственная, не монотонная и линейная. В тоже время, добавив к мажоритарной функции функцию голосования, получим функционально полную в Р2 систему, позволяющую согласно теореме Поста получить любую булеву функцию, в том числе и искомую. В этом можно убедиться, выполнив соответствующие преобразования.
Список литературы
1. Ерусалимский Я.М. Дискретная математика: теория задачи, приложения. – М.: «Вузовская книга», 1999. – 280 с.
2. Лавров И.А., Л.Л. Максимова. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: издательство «Наука», 1975. – 240 с. (и более поздние издания этой книги).
3. Г.П. Гаврилов, А.А. Сапоженко. Сборник задач по дискретной математике. М.: издательство «Наука», главная редакция физико-математической литературы. 1977 г. 368 с.
4. С.П. Плеханов. Симметричные карты - мощное средство минимизации булевых функций при проектировании цифровых устройств больших размерностей.// Электронная техника. Сер. 10. Микроэлектронные устройства. Вып. 4(88), 1991
Булевы векторы и единичный n-мерный куб
Вектор  , координаты которого принимают значение в множестве
, координаты которого принимают значение в множестве  , называется двоичным или булевым вектором.
, называется двоичным или булевым вектором.
Множество  называется единичным n-мерным кубом. Упорядоченная последовательность (кортеж) длины n называется вершиной единичного n-мерного куба. Мощность множества вершин единичного n-мерного куба равна
называется единичным n-мерным кубом. Упорядоченная последовательность (кортеж) длины n называется вершиной единичного n-мерного куба. Мощность множества вершин единичного n-мерного куба равна  .
.
На множестве вершин единичного n-мерного куба задаются следующие характеристики:
· Вес вектора или норма вектора, равный  ;
;
· Номер вектора, равный десятичному числу, записанному в двоичной системе счисления:  если разряды двоичного вектора нумеруются справа налево, начиная с 0, т.е.
если разряды двоичного вектора нумеруются справа налево, начиная с 0, т.е.  .
.
· Расстояние Хемминга между двумя булевыми векторами, равное числу разрядов, в которых эти векторы различаются, определяемое как  . Два вектора
. Два вектора  называются соседними, если расстояние Хемминга между ними равно 1, и противоположными, если расстояние Хемминга между ними равно n. Расстояние Хемминга является метрикой, а куб
называются соседними, если расстояние Хемминга между ними равно 1, и противоположными, если расстояние Хемминга между ними равно n. Расстояние Хемминга является метрикой, а куб  - метрическим пространством.
- метрическим пространством.
· На множестве булевых векторов длины n определено отношение предшествования:  . Нетрудно доказать, что отношение предшествования является отношением частичного порядка на множестве вершин единичного n-мерного куба.
. Нетрудно доказать, что отношение предшествования является отношением частичного порядка на множестве вершин единичного n-мерного куба.
· Неупорядоченная пара соседних вершин единичного n-мерного куба называется ребром куба.
· Множество  называется сферой радиуса k с центром
называется сферой радиуса k с центром  .
.
· Множество  называется шаром радиуса k с центром
называется шаром радиуса k с центром  .
.
· Последовательность вершин куба  называется цепью, соединяющей вершины
называется цепью, соединяющей вершины  и
и  , если
, если  . Число k называется длиной цепи.
. Число k называется длиной цепи.
· Множество  называется гранью куба
называется гранью куба  . Множество
. Множество  называется направлением грани, число k – рангом грани, а n- k - размерностью грани. Содержательно грань единичного n-мерного куба – это множество вершин, в которых координаты с индексами
называется направлением грани, число k – рангом грани, а n- k - размерностью грани. Содержательно грань единичного n-мерного куба – это множество вершин, в которых координаты с индексами  принимают одинаковые для всех вершин значения
принимают одинаковые для всех вершин значения  , а все остальные переменные принимают
, а все остальные переменные принимают  возможных наборов значений. Грани ранга k соответствует интервал ранга k. Например, интервал (-01-)={(0010), (0011), (1010), (1011)}. Переменные интервала, которым сопоставляются фиксированные для этого интервала значения из множества {0,1}, называются связанными, переменные, которым сопоставлены другие символы (например, -) называются свободными переменными интервала. Число связанных переменных интервала называется его рангом. Интервалу ранга k соответствует грань размерностью n- k, содержащая
возможных наборов значений. Грани ранга k соответствует интервал ранга k. Например, интервал (-01-)={(0010), (0011), (1010), (1011)}. Переменные интервала, которым сопоставляются фиксированные для этого интервала значения из множества {0,1}, называются связанными, переменные, которым сопоставлены другие символы (например, -) называются свободными переменными интервала. Число связанных переменных интервала называется его рангом. Интервалу ранга k соответствует грань размерностью n- k, содержащая  вершин куба.
вершин куба.
Дата: 2019-03-05, просмотров: 517.