Пусть имеем дифференциальное уравнение второго порядка 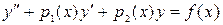 , (4.1)
, (4.1)
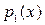 ,
,  ,
,  - непрерывные функции. И пусть известна фундаментальная система решений
- непрерывные функции. И пусть известна фундаментальная система решений 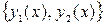 соответствующего однородного уравнения
соответствующего однородного уравнения 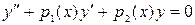 (4.2)
(4.2)
тогда 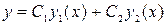 - есть общее решение уравнения (4.2).
- есть общее решение уравнения (4.2).
Будем искать решение уравнения (4.1) в виде 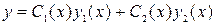 (4.3), где
(4.3), где 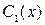 и
и 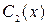 - неизвестные функции от х.
- неизвестные функции от х.
 .
.
На 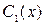 и
и  наложим следующее условие
наложим следующее условие 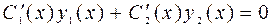 . (4.4)
. (4.4)
Тогда  . (4.5)
. (4.5)
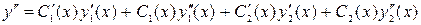 (4.6)
(4.6)
Подставляя (4.3), (4.5), (4.6) в (4.1) получим:
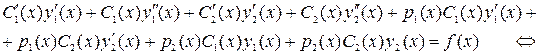
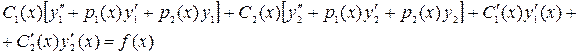
Так как  и
и 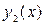 есть решение однородного уравнения (4.2) получаем:
есть решение однородного уравнения (4.2) получаем: 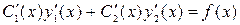 (4.7)
(4.7)
Значит функция  будет решением уравнения (4.1), если функции
будет решением уравнения (4.1), если функции 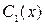 и
и  будут удовлетворять одновременно уравнениям (4.4) и (4.7), то есть системе:
будут удовлетворять одновременно уравнениям (4.4) и (4.7), то есть системе:
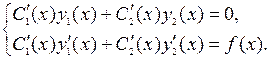 (4.8)
(4.8)
Определитель системы (4.8) – есть определитель Вронского линейно независимых решений  и
и 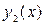 уравнения (4.2), то есть отличен от нуля. Поэтому система (4.8) имеет единственное решение:
уравнения (4.2), то есть отличен от нуля. Поэтому система (4.8) имеет единственное решение:

Подставляя эти выражения для 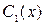 и
и 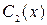 в (4.3), найдём частное решение (при
в (4.3), найдём частное решение (при  ,
,  ) уравнения (4.1)
) уравнения (4.1)
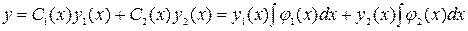 .
.
Общее решение дифференциального уравнения (4.1) будет
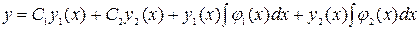 .
.
Пример 4.1. Решить уравнение 
Найдём решение характеристического уравнения 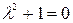 Þ
Þ 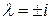 , запишем
, запишем  .
.
 будем искать в виде
будем искать в виде  , для этого рассмотрим и решим систему (4.8) для данного уравнения
, для этого рассмотрим и решим систему (4.8) для данного уравнения
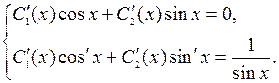 Û
Û 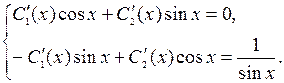
 Û
Û
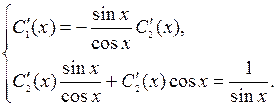 Û
Û 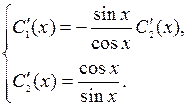 Û
Û 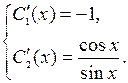 Û
Û 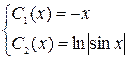 , получим
, получим 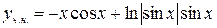 .
.
Итак 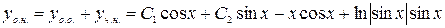 .
.
III. РЯДЫ.
ЧИСЛОВЫЕ РЯДЫ.
Вычисление суммы числового ряда.
Рассмотрим числовой ряд:
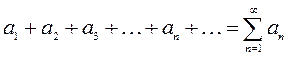 (1.1)
(1.1)
Сумма  первых членов ряда (1.1) называется его n-ой частичной суммой:
первых членов ряда (1.1) называется его n-ой частичной суммой: 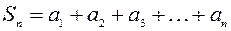
Ряд называется сходящимся, если существует конечный предел последовательности  его частичных сумм.
его частичных сумм. 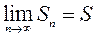
Число 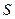 называют суммой ряда и обозначают
называют суммой ряда и обозначают 
Ряд называется расходящимся, если не существует или бесконечен предел последовательности частичных сумм 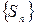 .
.
Теорема. Необходимый признак сходимости. Если числовой ряд 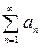 сходится, то предел его общего члена равен нулю
сходится, то предел его общего члена равен нулю  .
.
При исследовании ряда на сходимость необходимый признак обычно используют в следующей эквивалентной форме: если предел общего члена отличен от нуля или не существует, то ряд расходится.
Пример 1.1. Исследовать ряд на сходимость 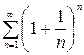 .
.
Применим необходимый признак сходимости. Для этого найдем предел общего члена ряда 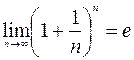 , так как он отличен от нуля, делаем вывод - искомый ряд расходится.
, так как он отличен от нуля, делаем вывод - искомый ряд расходится.
Пример 1.2. Найти сумму ряда  .
.
Воспользуемся определением сходимости ряда, предварительно упростив 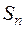 . Общий член ряда – правильная рациональная дробь. Применим метод неопределенных коэффициентов и представим общий член ряда как сумму элементарных дробей:
. Общий член ряда – правильная рациональная дробь. Применим метод неопределенных коэффициентов и представим общий член ряда как сумму элементарных дробей:
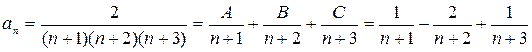
Имеем

| 
| 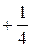
| ||||||
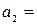
| 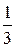
| 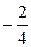
| 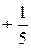
| |||||
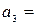
| 
| 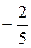
| 
| |||||
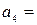
| 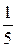
| 
| 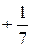
| |||||
| ……………………………………………………………………………… | ||||||||
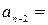
| 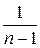
| 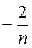
| 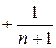
| |||||

| 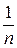
| 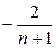
| 
| |||||
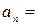
| 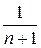
| 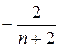
| 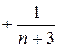
| |||||
Суммируя члены ряда (выделенные пунктиром слагаемые в суме дают нуль), получим:
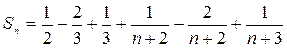 ,
, 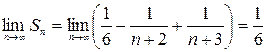 .
.
Значит, ряд сходится и его сумма 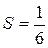 .
.
Дата: 2018-12-21, просмотров: 225.