Интегрирование по частям
Пусть u = u ( x ) и v = v ( x ) – непрерывно дифференцируемые (имеющие непрерывные производные) функции на отрезке [a , b], тогда
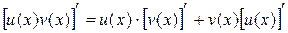 . (1.1)
. (1.1)
Интегрируя (1.1) в пределах от a до b с использованием формулы Ньютона-Лейбница, находим
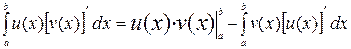 , (1.2)
, (1.2)
или, учитывая, что 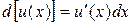 и
и  ,
,
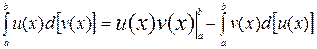 . (1.3)
. (1.3)
Для неопределенного интеграла имеем формулы
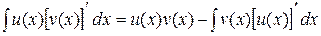
или
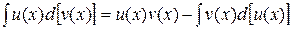 .
.
Замена переменной
Пусть выполняются следующие условия:
1) функция f ( x ) непрерывна на отрезке [a , b];
2) функция х= j ( t ) строго монотонна и непрерывна вместе со своей производной 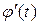 на отрезке [a , b];
на отрезке [a , b];
3) a = j ( a ), b = j ( b );
4) функция f(j(t)) определена и непрерывна на отрезке [a , b],
тогда справедливо равенство
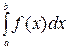 =
= 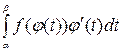 .
.  (1.4)
(1.4)
В случае неопределенного интеграла
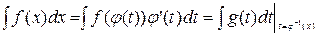 .
.

 Пример 1.1 Вычислить интеграл
Пример 1.1 Вычислить интеграл 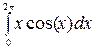 .
.
Решение.
Применим метод интегрирования по частям, опираясь на формулы (1.1), (1.2):
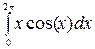 =
= 
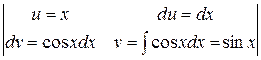 =
= 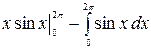 = =
= = 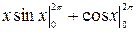 =
= 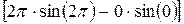 +
+ 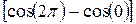 =0.
=0. 

 Пример1. 2 Вычислить
Пример1. 2 Вычислить 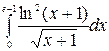 .
.
Решение:
Применим метод интегрирования по частям:
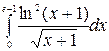 =
= 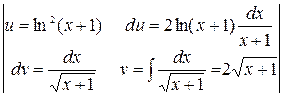 =
= 
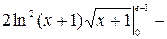
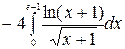 =
= 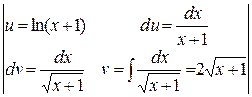 = 2
= 2 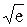
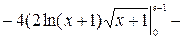
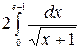 ) = 2
) = 2 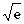 - 4(2
- 4(2 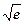 - 4
- 4 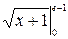 ) = 10
) = 10 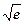 - 16.
- 16.
Пример 1.3 Вычислить определенный интеграл 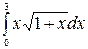 .
.
Решение.
Применим метод замены переменной с учетом формулы (1.3):
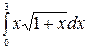 =
= 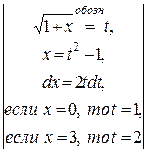 =
= 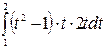 =
= 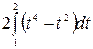 = =
= = 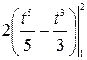 =
= 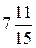 .
.
В достаточно простых случаях при интегрировании методом замены переменной можно не вводить обозначение новой переменной, а использовать прием внесения под знак дифференциала 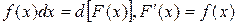 и инвариантность формул интегрирования.
и инвариантность формул интегрирования.
Пример 1.4 Вычислить 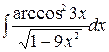 .
.
Решение.
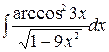 = -
= - 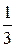
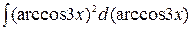 = -
= - 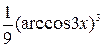 + C.
+ C.
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Для неправильной рациональной дроби (дробно-рациональной функции) 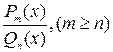 следует выделить целую часть :
следует выделить целую часть :
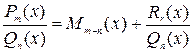 . (2.1)
. (2.1)
где 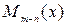 и
и 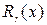 - многочлены степени
- многочлены степени 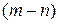 и
и 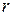 , причем
, причем 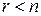 .
.
Разложение правильной дроби 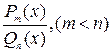 на сумму простейших дробей имеет вид:
на сумму простейших дробей имеет вид:
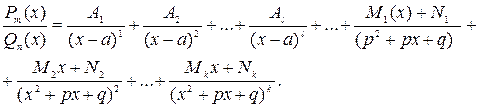 (2.2)
(2.2)
Для вычисления коэффициентов 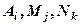 следует последнее равенство (2.2) привести к общему знаменателю, приравнять коэффициенты при одинаковых степенях
следует последнее равенство (2.2) привести к общему знаменателю, приравнять коэффициенты при одинаковых степенях 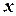 в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной
в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной 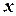 произвольные числовые значения.
произвольные числовые значения.
Простейшие дроби 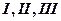 типов в правой части (2.2) интегрируются следующим образом:
типов в правой части (2.2) интегрируются следующим образом:
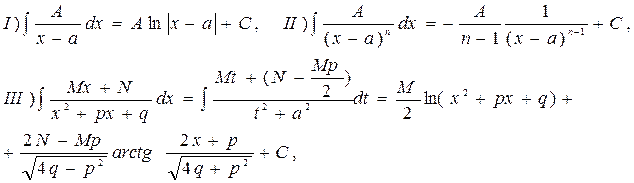
где трехчлен 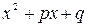 не имеет действительных корней,
не имеет действительных корней, 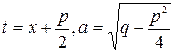 . Дроби четвертого типа интегрируются так:
. Дроби четвертого типа интегрируются так:
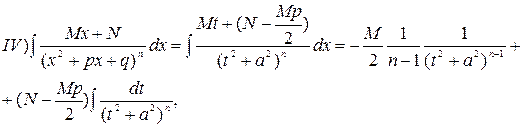
причем при 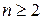 интеграл
интеграл 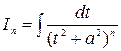 вычисляется по рекуррентной формуле:
вычисляется по рекуррентной формуле:
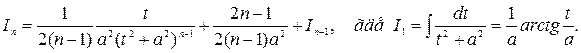
Пример2.1 Вычислить 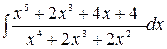 .
.
Решение.
Подынтегральная функция – неправильная рациональная дробь. Представим ее в виде суммы многочлена и правильной рациональной дроби (например, способом деления числителя на знаменатель) как в (2.1):
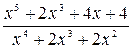 =
= 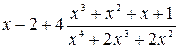 .
.
Следовательно:
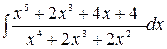 =
= 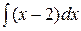 + 4
+ 4 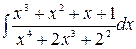 . (2.3)
. (2.3)
Разложим знаменатель дроби на множители:
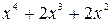 =
= 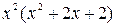 , где квадратный трехчлен
, где квадратный трехчлен 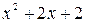 не имеет действительных корней.
не имеет действительных корней.
Согласно (2.2) можно записать в виде:
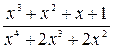 =
= 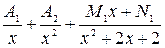 . (2.4)
. (2.4)
Для определения коэффициентов 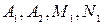 дроби в правой части равенства (2.4) приведем к общему знаменателю и сложим. В результате получим равенство двух дробей с одинаковыми знаменателями. Следовательно, числители дробей в левой и правой частях полученного равенства должны быть равны, т.е.:
дроби в правой части равенства (2.4) приведем к общему знаменателю и сложим. В результате получим равенство двух дробей с одинаковыми знаменателями. Следовательно, числители дробей в левой и правой частях полученного равенства должны быть равны, т.е.:
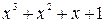
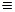
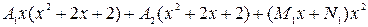 .
.
Два многочлена относительно переменной 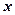 тождественно равны тогда и только тогда, когда их коэффициенты при одинаковых степенях
тождественно равны тогда и только тогда, когда их коэффициенты при одинаковых степенях 
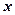 равны между собой.
равны между собой.
Приравняем эти коэффициенты и получим систему уравнений относительно 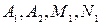 :
:
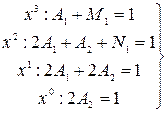
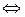
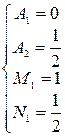 .
.
Подставив найденные коэффициенты 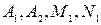 в (2.4), получим:
в (2.4), получим:
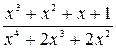 =
= 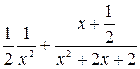 . (2.5)
. (2.5)
Из (2.3) и (2.5) следует, что:
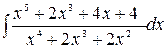 =
= 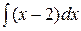 +4
+4 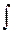 (
( 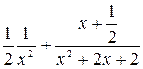 )
) 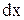 =
= 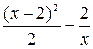 + 2
+ 2 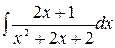 =
= 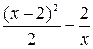 + 2
+ 2 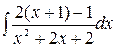 =
= 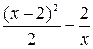 + 2
+ 2 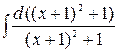
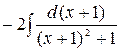 =
= 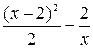 +
+ 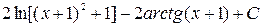 .
.
Дата: 2018-12-21, просмотров: 223.