Сущность метода
Метод характеризуется относительно малым постоянным шагом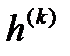 
= h, который задаётся как параметр метода.
Идея метода видна из простого соотношения:
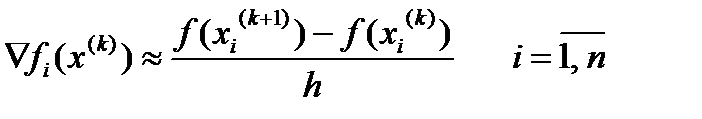(5.75)
где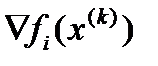 
– i -я составляющая вектора - градиента функции в точке x ( k ) .
При заданном малом шаге h алгоритм метода определяется формулой (5.74).
Замечание
Хотя шаг поиска h должен быть малым, но не меньше порога чувствительности функции:
| f(x(k+1)) - f(x(k)) | > d
где d - максимальная вычислительная погрешность ПЭВМ.
Окончание численной процедуры поиска минимума функции может определяться выполнением следующего условия.
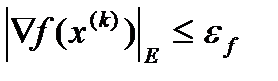
где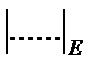 
- евклидова норма вектора, 
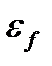- малая положительная величина, задаваемая как параметр.
Графически метод простой градиентной минимизации в двумерном пространстве иллюстрируется на рис. 5.18.
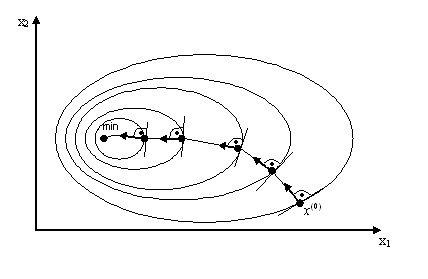
Рис. 5.18
Недостатки
· Основным недостатком метода является его низкая эффективность с точки зрения количества шагов поиска, а также с точки зрения затрат машинного времени.
· Метод склонен к зацикливанию в местах резкого изменения направления «оврага» целевой функции.
Преимущества
· Метод прост при программной реализации.
Метод надежен при использовании его в условиях сложной поверхности целевой функции.
Блок-схема метода простой градиентной минимизации:
| НАЧАЛО |
| gradF[1] := 100; gradF[2] := 100; h := 0.000001; CaseSwitch := 0; Sol := false; |
| alfa <> 0 |
| CaseSwitch := CSwitch(X[1], X[2]) |
| then |
| else |
| А while (((Abs(gradF[1]) > Eps) and (Abs(gradF[2]) > Eps)) and (Sol = false)) do |
| gradF[1] :=…; gradF[2] :=…; |
| 2 |
| 2 |
| X[1] := X[1] - h * gradF[1]; X[2] := X[2] - h * gradF[2]; |
| n = 1000 |
| Sol := true; |
| then |
| else |
| A |
| GetSolution := Sol; |
| КОНЕЦ |
Примеры работы программы:
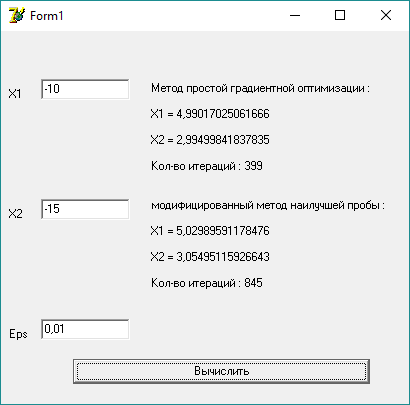
В данном примере введена начальная точка (-10;-15) и точность 0,01. Программа приходит к точке (5; 3), что является минимумом целевой функции.
Метод простой градиентной оптимизации сходится за 399 итераций, а модифицированный метод наилучшей пробы за 845 итераций.
Выводы
В первой части курсовой работы я находила безусловный минимум целевой функции с помощью метода простой градиентной оптимизации и модифицированного метода наилучшей пробы.
Метод простой градиентной оптимизации сходится за 399 итераций, а модифицированный метод наилучшей пробы за 845 итераций.
Листинг метода случайного поиска с направляющей сферой:
procedure TMetNaiProb.Executing(var X : TVectorMass; Eps : real;var n : integer);
var
h,hrab,A1,A2: real;
g1 : array[1..100] of real;
g2 : array[1..100] of real;
g3 : array[1..100] of real;
m,i: integer;
begin
n:=2;
m:=20;
h:=0.1;
hrab:=0.3;
A1:=0;
A2:=F(X[n-1,1],X[n-1,2]);
while (Abs(A2-A1)>Eps) Do
begin
A2:=A1;
for i:=1 to m do
begin
g1[i]:=Random(100)-50;
g2[i]:=Random(100)-50;
g3[i]:=Power((g1[i]*g1[i])+(g2[i]*g2[i]),0.5);
if g3[i]=0 then
g3[i]:=1;
g1[i]:=g1[i]/g3[i];
g2[i]:=g2[i]/g3[i];
end;
for i:=1 to m do
begin
A1:=F(X[n-1,1]+g1[i]*h,X[n-1,2]+g2[i]*h);
if A1<A2 then
begin
X[n,1]:=X[n-1,1]+g1[i]*hrab;
X[n,2]:=X[n-1,2]+g2[i]*hrab;
n:=n+1;
end;
end;
end;
n:=n-2;
end;
function TMetNaiProb.F(X1, X2 : real) : real;
begin
F := Power(X1 - 5, 2) + 2 * Power(X2 - 3, 2);
end;
Листинг метода простой градиентной минимизации:
procedure TOptGradMeth.GetSolution(var X : TVectorMass; Eps : real; var n : integer);
var
gradF : TVector;
h, step : real;
begin
n := 1;
h := 0.1;
gradF[1] := 100;
gradF[2] := 100;
while ((Abs(gradF[1]) > Eps) or (Abs(gradF[2]) > Eps)) do
begin
gradF[1] := (F(X[n, 1] + h, X[n, 2]) - F(X[n, 1], X[n, 2])) / h;
gradF[2] := (F(X[n, 1], X[n, 2] + h) - F(X[n, 1], X[n, 2])) / h;
n := n + 1;
X[n, 1] := X[n - 1, 1] - h * gradF[1];
X[n, 2] := X[n - 1, 2] - h * gradF[2];
end;
end;
function TOptGradMeth.F(X1, X2 : real) : real;
begin
F := Power(X1 - 5, 2) + 2 * Power(X2 - 3, 2);
end;
Дата: 2018-12-21, просмотров: 221.
