Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Постановка задачи

Рассматривается задача оптимизации целевой скалярной функции 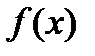 по аргументам (параметрам) 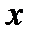, на вариации которых никаких ограничений не накладывается.

                                                             

    Моему варианту № 5 соответствуют следующие данные:

 

f(x₁, x₂) = 2 (х₁ – 5)² + (х₂ – 8)²

        

16	Модифицированный метод наилучшей пробы
	Метод простой градиентной оптимизации

 

 

Модифицированный метод наилучшей пробы

Суть метода

Этот метод в отличие от предыдущего позволяет выбирать наилучшее направление изменения функции (при этом оно не обязательно совпадает с антиградиентом функции).

Алгоритм метода

Из некоторой промежуточной точки поиска минимума целевой функции x ^{( k )} осуществляется m-случайных независимых пробных шагов:

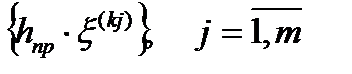                                                        (5.52)

Также, как и ранее (см. предыдущий метод) x ^{(к j )}- единичные случайные независимые векторы с равномерной функцией распределения вероятности внутри шара единичного радиуса (в частном случае – круга).

Наилучшим направлением считается направление, в котором функция достигает минимального значения.

f(x^(k)+h_прx^(kj*)) = min f(x^(k)+h_прx^(kj)),                         (5.53)

                                  

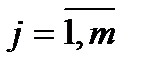
В этом направлении - x^(kj*) совершается рабочий шаг движения:

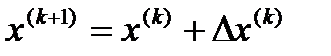 ,                                         (5.54)

где 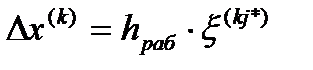   .                                                 (5.55)

Из формул (5.52)-(5.55) следует, что эффективность метода определяется следующими параметрами метода, задаваемыми оператором:

h _пр , h _раб , m.

Они, как правило, входят в состав формальных параметров компьютерной подпрограммы, реализующей данный метод.

Замечание

Можно показать, что в пределе при m стремящемся к ¥ , направление x ^{( kj *)} стремится к антиградиенту функции, то есть:

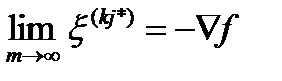                                            (5.56)

Преимущества метода

- Метод позволяет при количестве проб m < n получить направление x ^{( kj *)} близкое к антиградиенту функции.

- Метод просто программируется.

- Позволяет определить глобальный экстремум (в принципе).

Недостатки метода

- Метод не исключает выбор «наилучшего» из m-направлений , в котором функция f(x) будет возрастать !

- Накопленная при m-проб информация о поведении целевой функции используется не эффективно.

 

Модификация метода наилучшей случайной пробы

В ответ на 1-ый недостаток рассмотренного метода возникла идея дополнить процедуру (5.53) операцией, присущей методу простой случайной оптимизации.

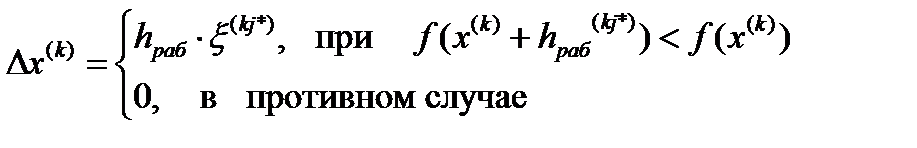(5.57)

С помощью такого условного оператора будет исключена возможность роста функции при неудачных случайных пробах.

 

Блок-схема модифицированного метода наилучшей пробы

1.

А while(Abs(A2-A1)>Eps) Do

B for i:=1 to m do

g1[i]:=Random(100)-50; g2[i]:=Random(100)-50;

НАЧАЛО

n:=2;m:=20; h:=0.1; hrab:=0.15; A1:=0;

A2:=A1;

A2:=F(X[n-1,1],X[n-1,2]);

2

Блок-схема основного метода:

 

2

then

else

g1[i]:=g1[i]/g3[i]; g2[i]:=g2[i]/g3[i];

B

g3[i]:=Power((g1[i]*g1[i])+(g2[i]*g2[i]),0.5);

3

g3[i]:=1;

g3[i]=0

C for i:=1 to m do

 

 

КОНЕЦ

3

then

else

n:=n-2;

A1<A2

C

A

A1:=F(X[n-1,1]+g1[i]*h,X[n-1,2]+g2[i]*h);

X[n,1]:=X[n-1,1]+g1[i]*hrab; X[n,2]:=X[n-1,2]+g2[i]*hrab; n:=n+1;