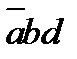Операция конъюнкция (называемая двоичным умножением) совпадает с арифметической операцией умножения над числами 0, 1, т. е.:
0 ∙ 1=0; 0 
1 ≡ 0;
0 ∙ 0=0; 0 
0 ≡ 0;
1 ∙ 0=0; 1 0 ≡ 0;
1 ∙ 1=1; 1 1 ≡ 1.
Обычное арифметическое сложение выводит за пределы множества {0;1}. Поэтому рассматривают операцию, называемую двоичным сложением и обозначаемую символом «+», которая определяется следующей таблицей истинности:
42
| x | y | x + y |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Для двоичного сложения имеют место все основные арифметические законы:
1) коммутативность: x + y ≡ y + x;
2) ассоциативность: (x + y) + z ≡ x + (y + z);
3) дистрибутивность умножения относительно сложения:
x(y + z) ≡ xy + xz.
Справедливость этих законов может быть установлена путём составления таблиц истинности.
Из определения операции двоичного сложения (см. таблицу 8) следует, что x + y ≡ 0 при x ≡ y, т.е. x + x ≡ 0. Имеет место и равносильность x + 0 ≡ x. В этом можно убедиться, составив соответствующую таблицу истинности.
Выразим основные логические операции через конъюнкцию, двоичное сложение и константу 1:
1) операция отрицания: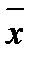 
≡ x + 1;
для доказательства достаточно составить таблицу истинности (таблица 9); из неё видно, что при одинаковых значениях х формулы 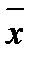и x + 1 принимают одинаковые значения;
х 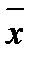x + 1
0 1 1
1 0 0
43
2) дизъюнкция:
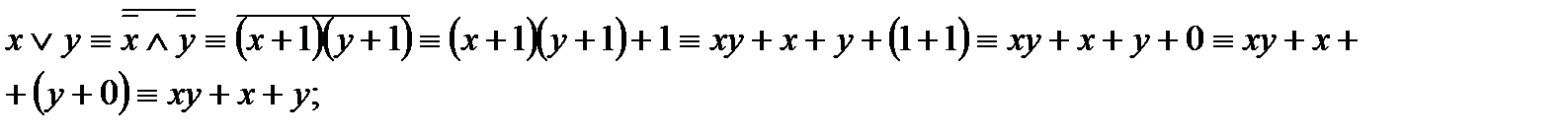
3) импликация:
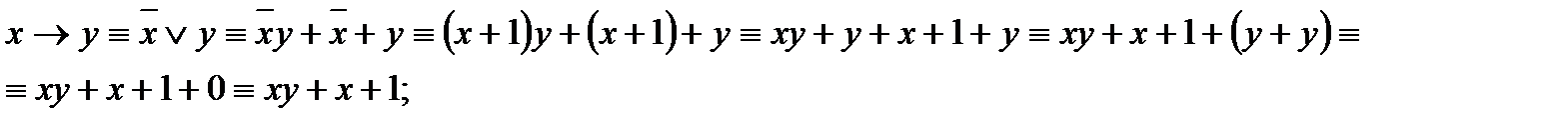
5) двойная импликация:
,
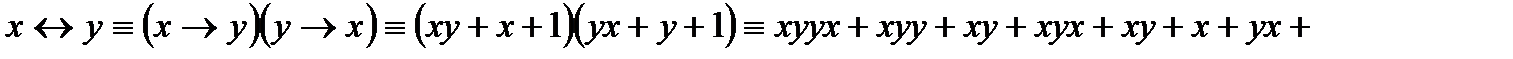
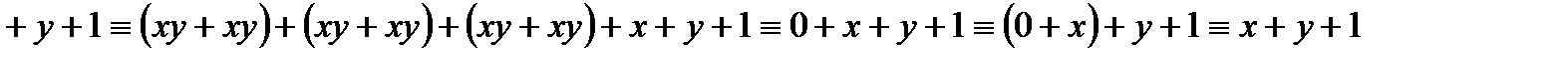т. к. xy + xy ≡ 0 (в силу равносильности х + х ≡ 0), х + 0 ≡ х.
Таким образом, имеют место равносильности:
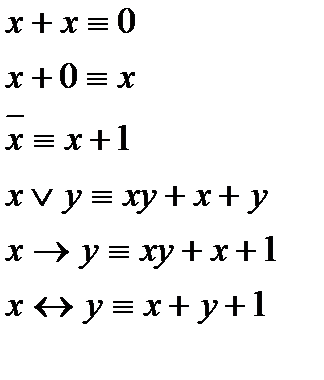
Эти равносильности позволяют переводить формулы, содержащие знаки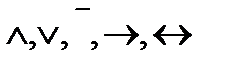 
, в равносильные им формулы, содержащие лишь знаки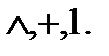 
Формулы, содержащие лишь знаки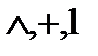 
, называются полиномами (многочленами).
Полином вида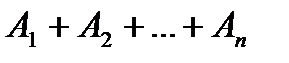 
, где каждая из формул 
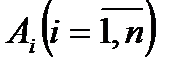есть либо константа (0 или 1), либо элементарная переменная, либо конъюнкция элементарных переменных, в которой каждая переменная встречается не более одного раза, при этом все 
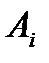различны, называется полиномом (многочленом) Жегалкина.
Например, x(y + yz), xy + xyz – полиномы Жегалкина.
44
Любая булева функция может быть представлена многочленом Жегалкина (причём, единственным образом). Для этого используются равносильные преобразования.
Пример 1. Представить функцию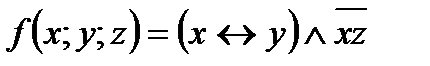 
в виде полинома Жегалкина.
Решение:
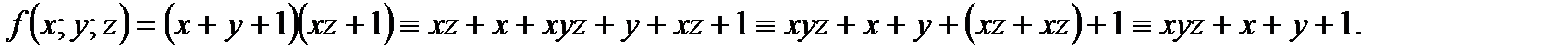
Пример 2. Представить функцию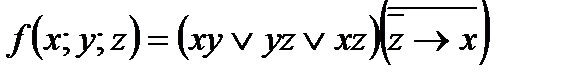 
в виде полинома Жегалкина.
Решение:
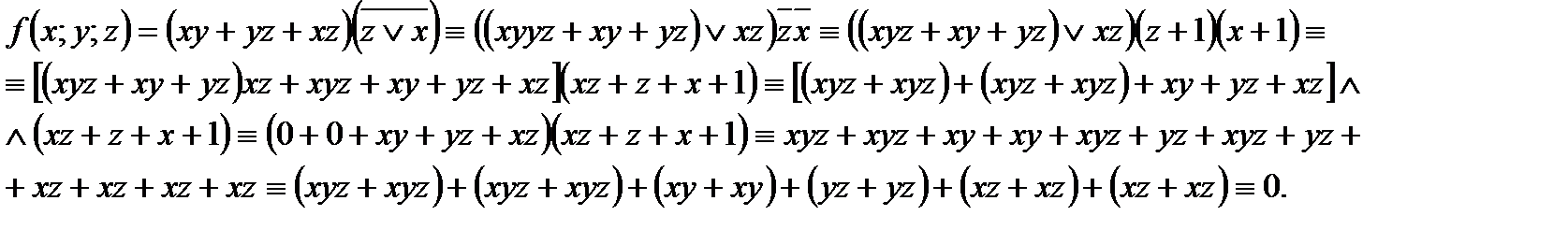
Примеры решения задач рассмотрены на третьем и четвертом обзорных установочных занятиях.
Пример 1:
Задать формулой функцию f (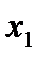 
; 
; 
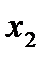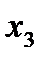) , имеющую таблицу истинности:
| Таблица истинности | ||||
| 
| 
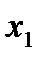
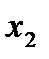
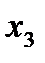
| f( ; ; )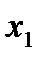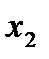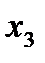
| |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 1 | |
45
Решение: для наборов значений переменных (1;1;0), (1;0;1), (0;1;0), (0;0;0), на которых функция принимает значение 1, запишем конъюнкции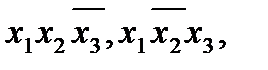 
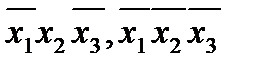, а искомая формула имеет вид:
f ( ; ; )=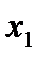 
.
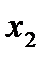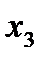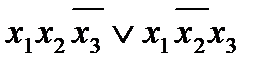
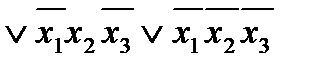Пример 2:
Найти формулу, определяющую функцию f(x; y; z), по заданной таблице истинности. Упростить полученную формулу.
| Таблица истинности | |||
| х | y | z | f(х; y; z) |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
Решение: используя правило получения формулы из таблицы истинности для функции f(x; y; z), имеем: f(x; y; z) =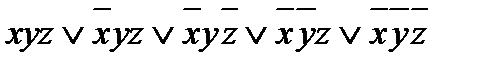 
.
Упрощаем полученную формулу, используя формулы логики:
f(x; y; z) =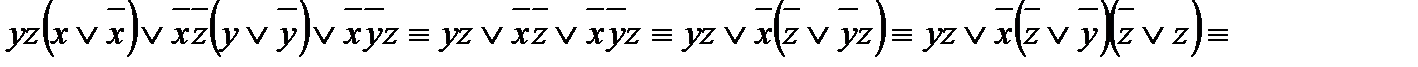 
.
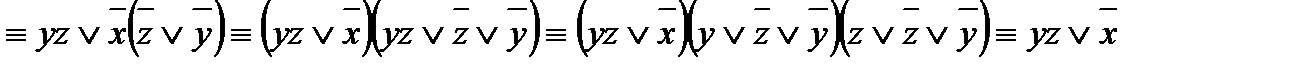Таким образом, f(x; y; z) =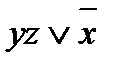 
.
Пример 3. Привести функцию f(x; y; z) =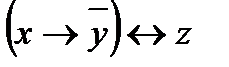 
к ДНФ.
Решение:
f(x; y; z) =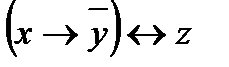 
.
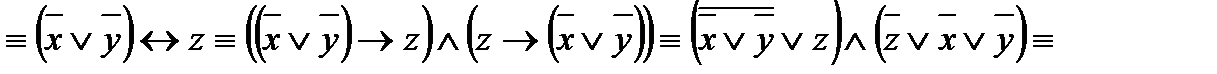
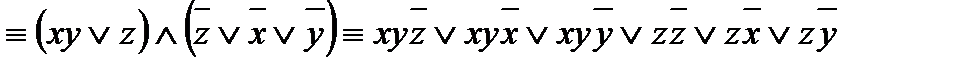Функция f(x; y; z) уже записана в виде ДНФ. Но её можно упростить:
f(x; y; z) =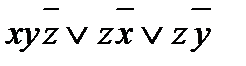 
.
46
Пример 4. Найти СДНФ для функции f(x; y; z) =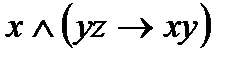 
.
Решение:
1) ищем ДНФ для данной функции:
f(x; y; z) =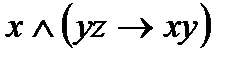 
;
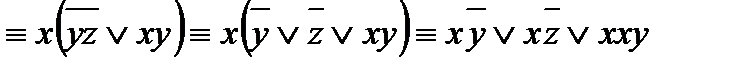2) конъюнкция xxy содержит переменную x дважды, поэтому используем равносильность x 
x ≡ x:
f(x; y; z) =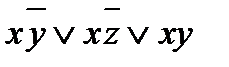 
;
3) элементарные конъюнкции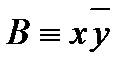 
и С ≡ xy не содержат переменной z, а элементарная конъюнкция 
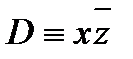не содержит переменной y , поэтому используем равносильности 
, 
, 
:
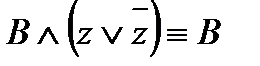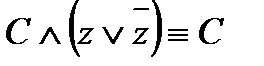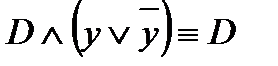f(x; y; z) =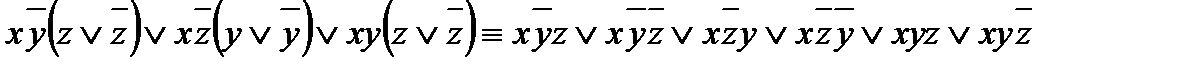 
;
4) теперь ДНФ содержит две одинаковые элементарные конъюнкции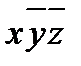 
и две одинаковые элементарные конъюнкции 
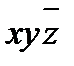, поэтому лишние отбрасываем, используя равносильности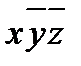 
≡ , 
≡ :
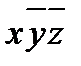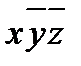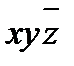
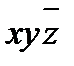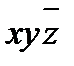f(x; y; z) =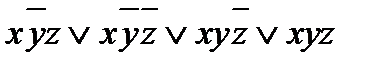 
.
Таким образом, функция f(x; y; z) записана в виде ДНФ.
Пример 5. Дана функция f(x; y; z) = 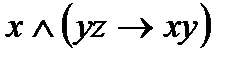. Записать её в виде СДНФ путём составления таблицы истинности.
Решение: составляем таблицу истинности:
| х | y | z | yz | xy | yz→xy | f(x; y; z) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
47
Тогда СДНФ для данной функции будет выглядеть так:
f(x; y; z) =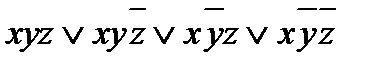 
.
Пример 6. Метод Карно.
Покажем карты Карно для функций от двух, трех и четырех переменных:
B
| 01 | ||||||||
| 10 | 11 |
| 000 | 010 | 011 | 001 |
| 100 | 110 | 111 | 101 |
| 0000 | 0010 | 0011 | 0001 |
| 0100 | 0110 | 0111 | 0101 |
| 1100 | 1110 | 1111 | 1101 |
| 1000 | 1010 | 1011 | 1001 |
По карте можно составить СДНФ и СКНФ, как по таблице истинности. Мы показали , какие наборы соответствуют каждой ячейке. Для задания функции по карте в ячейке указывается значение функции на данном наборе. Необходимо составить СДНФ:
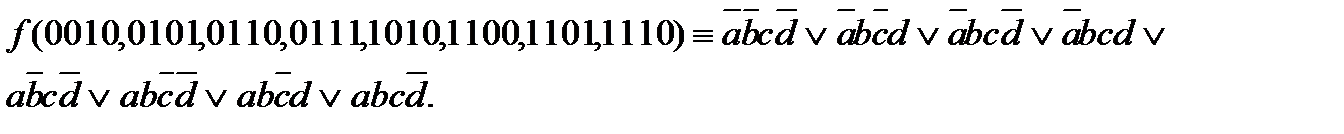
Минимизируем функцию с помощью карты.
|
| 0 |
| ||||
| 0 | 1 | 1 | 1 | ||||
| 1 | 0 | 1 | ||||
| 0 | 1 | 0 | 0 |
|
|
48
Получим ДНФ: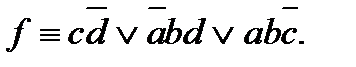 
Пример 7. Представить функцию 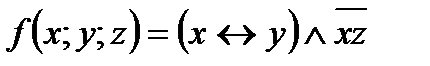в виде полинома Жегалкина.
Решение:
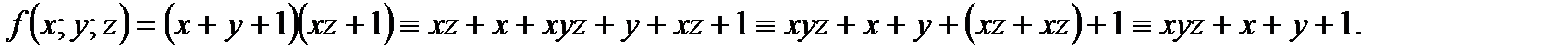Пример 8. Представить функцию 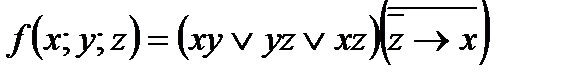в виде полинома Жегалкина. Решение:
После изучения теории и решения примеров по данной теме можно решить задание №4 и №5 контрольной работы.
Логика предикатов.
Изучить по учебной литературе вопросы:
4.1. Предикаты. Основные понятия.
4.2. Следование одного предиката из другого. Равносильность предикатов. Равносильные преобразования.
4.3. Логические операции над одноместными предикатами.
4.4. Кванторные операции над одноместными и двуместными предикатами.
4.5. Построения отрицаний к предикатам, содержащим кванторы.
4.6. Запись математических утверждений с помощью логики предикатов.
Предикаты. Основные понятия.
Предикат – это предложение с одной или несколькими переменными, становящееся высказыванием при постановке вместо переменных конкретных значений.
Пример: «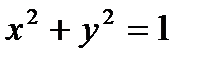 
» - предикат, т. к. при подстановке x=1, y=0 предложение « 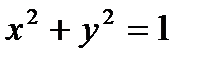» становится истинным высказыванием, а при подстановке 
, 
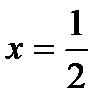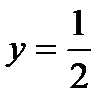– ложным высказыванием. 49
«Он пошёл в кино» - предикат, в котором переменная – «он».
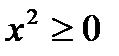– предикат. Это предложение становится истинным высказыванием при подстановке любого вещественного числа x.
Наличие переменной в предложении необязательно делает это предложение предикатом. Нужно всегда смотреть на то, какие предложения получаются при подстановке конкретных значений переменной, а именно – будут ли они высказываниями.
В предикат можно подставлять вместо переменных не все значения, а лишь взятые из какого-либо множества. Множество всех таких значений называется областью определения предиката.
«Он пошёл в кино». Область определения: ученик, житель, но не число 2.
Обычно область определения предиката задают заранее.
Одноместный предикат (имеющий одну переменную) определяет отношение принадлежности некоторому множеству. Принято одноместный предикат называть предикатом-свойством, n- местный (имеющий n переменных, для n>1) – предикатом-отношением, 0- местный предикат – высказыванием.
Полный прообраз (1) при Р называют множеством истинности Т(Р) предиката Р.
§4.2. Следование одного предиката из другого. Равносильность предикатов. Равносильные преобразования.
Предикат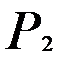 
следует из предиката 
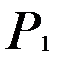, если импликация 
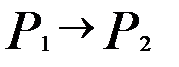обращается в истинное высказывание при любых наборах значений переменных, входящих в неё.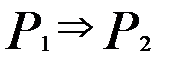 
Тогда 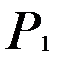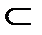Т( ) 
Т(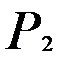 
)
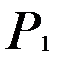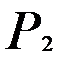Пусть даны два предиката, определенные на одном множестве. Предикаты и называются равносильными, если при любом наборе значений переменных, входящих в них, предикаты принимают одинаковые значения истинности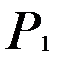: Т( )=Т( )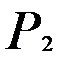
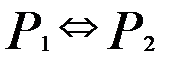
Тогда равносильным преобразованием предиката называется его замена на равносильный предикат. Эти свойства предиката используются при решении уравнений и неравенств. Так, решение любого уравнения или неравенства предусматривает установление множества его истинности, т.е. множества истинности соответствующего ему предиката. В процессе поиска множества истинности производят замену одного предиката другим, равносильным данному, с целью упрощения.
Пример.
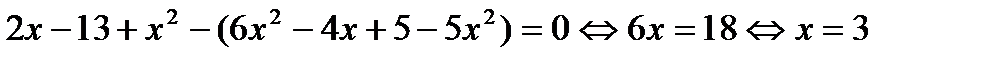
т.е. множество истинности каждого из этих уравнений состоит из одного числа 3. 50
Дата: 2018-11-18, просмотров: 1094.
