Кафедра Методики преподавания математики
КУРСОВАЯ РАБОТА
Эвристические методы поиска
Способа решения задач
Выполнила студентка
математического факультета
4 курса группы М - 43
Гагаринова Ольга
Научный руководитель:
ассистент Шилова З.В.
Киров 2003
СОДЕРЖАНИЕ
Введение.
1. Структура процесса решения задач. Поиск способа решения задач.
2. Эвристический метод решения задач, его понятие.
3. Система эвристических методов Л.М. Фридмана/
3.1 Метод разбиения задачи на подзадачи.
3.2 Метод преобразования задачи.
3.3 Метод моделирования.
3.4 Метод вспомогательных элементов.
4. Система эвристических методов М.Б. Балка/
4.1 Аналогия.
4.2. Индукция.
4.3 Предельный случай.
4.4 Соображения непрерывности.
Заключение.
ВВЕДЕНИЕ
В настоящее время во всех сферах человеческой жизнедеятельности – науке, технике, народном хозяйстве и др. – возникают вопросы, проблемы нестандартного характера, разрешение которых зачастую невозможно осуществить посредством стандартных приемов, методов, ставших уже привычными. Условия жизни ставят всех нас перед необходимостью полного применения своих способностей и психо-физических ресурсов для решения сложных, нестандартных задач, что в итоге приводит к психическому и физическому перенапряжению, истощению жизненных сил. Такое положение вещей приводит нас к необходимости научиться решать подобные задачи с наименьшим объемом затрат. Известный психолог XX века В.Н.Пушкин по этому поводу высказывал свое мнение: “Человек должен совершить некоторую совокупность действий, решить ту или иную задачу, однако наличные условия не подсказывают ему способа решения этой задачи… . Чтобы найти выход из подобной ситуации, человеку необходимо создать новую, не имевшуюся у него ранее стратегию деятельности, т.е. совершить акт творчества”. В итоге встает вопрос об универсальном методе действий, который включает в себя продуктивный способ мышления, характер (направленность) действий, позволяющем разрешить поставленную проблему.
В науке давно известен и до сих пор совершенствуется такой метод. Название его – эвристический метод. Эвристическая деятельность является “разновидностью человеческого мышления, которая создает новую систему действий или открывает ранее неизвестные закономерности …”[7, стр.6].
С точки зрения американского математика Дердье Пойа цель эвристики – исследовать правила и методы, ведущие к открытиям и изобретениям.
Однако, по мнению того же В.Н.Пушкина, эвристика-наука исследует закономерности эвристической как творческой деятельности человека.
В виду этого несложно усмотреть, что эвристика, в частности, эвристические приемы, методы оказывают достаточно сильное влияние на развитие творческих способностей, и, что не менее важно, на развитие творческого мышления.
Поэтому оказывается очень важным прививать новому поколению эвристические знания, а значит, обучать в школе эвристическому мышлению. Лучше всего это можно осуществить на уроках математики, изучая “общие приемы поиска решения задач, пригодных к любым, в том числе и “нетиповым”, нестандартным задачам”, иначе, обучая владению эвристическими приемами (методами) решения математических задач.
В связи с этим, целью данной работы является изучение эвристических методов решения математических задач.
В процессе выполнения работы необходимо было решить следующие задачи:
● во-первых, для осознания сути решения математической задачи важно было изучить структуру решения задачи;
● было рассмотрено понятие эвристического метода решения задачи и трактовка его особенностей с различных позиций;
● далее нужно было изучить соответствующие эвристические системы методов решения задач русских математиков Л.М. Фридмана и М.Б. Балка;
● в работе излагаются обе системы эвристических методов, причем система методов Л.М. Фридмана иллюстрируется примерами задач, подобранными самостоятельно;
● кроме того, в работе сравниваются две данные системы эвристических методов на основе выделения особенностей каждой.
Метод моделирования
Этот метод состоит в замене исходной задачи другой задачей, моделью исходной. Примером использования такого метода является широко применяемый метод решения текстовых (сюжетных) задач путем составления уравнения или системы уравнений. Приведем пример использования этого метода.
Задача 8. В квартире десять лампочек. Сколько существует различных способов освещения квартиры? Два способ освещения считаются различными, если они отличаются состоянием хотя бы одной лампочки. Каждая лампочка может гореть и не гореть. Случай, когда все лампочки не горят, - это тоже способ освещения.
Решение. Чтобы легче подсчитать все различные способы освещения квартиры, изобразим каждую лампочку в виде квадрата, а ее состояние будем отмечать знаком “+”, если лампочка горит, и знаком “ – ” в противоположном случае.
Тогда каждому способу освещения квартиры будет соответствовать строка из десяти квадратов со знаком “+” или “ – ”.
| + | + | – | – | + | – | + | + | – | – |
Число же таких строк в таблице и есть искомое число различных способов освещения квартиры
Исходя из выше сказанного, получаем следующую задачу.
Имеем прямоугольную таблицу, содержащую 10 столбцов. В каждой клетке стоит “+” или “ – ”. Любые две строки таблицы отличаются знаками в клеточках, стоящих хотя бы в одном и том же столбце. Какое наибольшее число строк имеет эта таблица?
Если решение этой задачи не очевидно, то можно рассматривать каждую строку таблицы, о которой идет речь в предыдущей задаче, как десятичное число, составленное из цифр 1 и 0 ( 1 ~ “+”, 0 ~ “ – ”). Тогда вопрос задачи будет звучать следующим образом: сколько различных десятизначных чисел можно образовать из цифр 0 и 1? (При этом числа, в записи которых слева стоят одни нули, например, 0100001101 или 0000000001 или даже, 0000000000, также рассматриваются).
Решение. На каждом месте в записи десятизначного числа могут стоять лишь цифры 1 и 0. Поэтому имеется лишь две комбинации цифр на каждом месте. Эти комбинации независимы друг от друга, так как проставление цифры на данном месте в записи числа не зависит от того, какие цифры стоят на других местах. Поэтому общее число комбинаций или возможных десятичных различных чисел равно 2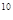 
= 1024.
Итак, ответ: общее число способов освещения квартиры равно 1024.
Задача 9. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.
Данная задача легко решается, если построить физическую или векторную ее модели.
Физическая модель. Для построения физической модели нужно вспомнить положения курса физики: 1) центр тяжести двух материальных точек с одинаковой массой лежит в середине отрезка, соединяющего эти точки, с массой, равной сумме масс этих точек;
2) центр тяжести двух материальных точек с различной массой лежит в точке, делящей отрезок в отношении масс (большей массе соответствует меньший отрезок и, наоборот);
3) Центр тяжести системы точек находится путем нахождения центра тяжести пар точек из этой системы, и при этом он не зависит от того , в каком порядке соединяются эти точки попарно.
Решение. Докажем сначала, что медианы треугольника пересекаются в одной точке. Для этого определим центр тяжести системы вершин треугольника. В вершины треугольника – как материальные точки поместим массы по 1 в каждую. Тогда, по 1) положению центр масс каждой пары вершин находится в середине отрезка с концами в этих вершинах.
 |
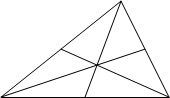Так как 2)середины сторон треугольника – основания медиан, то получаем, что каждая медиана этого треугольника имеет на своих концах массы 1 и 2, считая от вершин треугольника.
3) Пользуясь третьим положением, получим, что точка равновесия каждой медианы имеет массу равную трем. Это говорит о том, что точки равновесия медиан совпадают, то есть медианы пересекаются в одной точке. Используя второе положение, получаем, что данной точкой равновесия каждая медиана делится на два отрезка, которые будут находиться в отношении 2 к 1, считая от вершин треугольника.
Векторная модель. Для доказательства данного утверждения необходимо вспомнить формулу деления отрезка в данном отношении для векторов.
Итак, пусть точка M делит отрезок AB так, что AM=λMB (*), тогда для любой точки О выполнимо следующее векторное соотношение: . .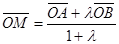 
, где λ≠ – 1.
Чтобы доказать эту формулу, возьмем векторы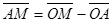 
и 
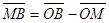. Подставляя эти соотношения в формулу (*), получаем
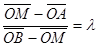, иначе 
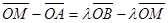. Группируя векторы 
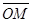, получаем выражение 
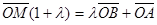. Отсюда
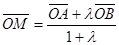, где λ≠ – 1.
Решение. Выберем произвольную точку О в качестве общего начала векторов.
 |
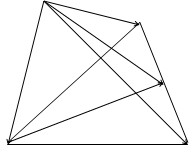На медиане А А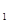 
возьмем точку G, делящую ее C в отношении 2 : 1, считая от точки А. Тогда на основании формулы деления отрезка в данном отношении будем иметь: 
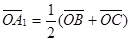и GА₁
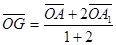.А В
Тогда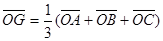 
для произвольной точки О.
В это выражение векторы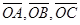 
входят равноправно, поэтому векторы к точкам, делящих медианы в отношении 2 : 1, будут иметь то же выражение. Это означает, что делящие точки совпадают.
Аналогия
В математике зачастую имеют место такие случаи, когда аналогичные, сходные условия приводят к сходным результатам. Чтобы таким положением было возможно воспользоваться, необходимо научиться (хотя бы на небольшом числе упражнений) формулировать математические предложения по аналогии. Но также нельзя забывать, что сравнение не является доказательством и предложения, сформулированные по аналогии, могут оказаться ошибочными.
И хотя предложения, сформулированные по аналогии, могут оказаться ошибочными, все же часто оказывается, что такие предложения истинны.
Но не только для формулировки новых правдоподобных математических фактов полезно привлекать аналогию, поскольку еще более ценно научиться сознательно привлекать аналогию при поиске способа решения трудной задачи.
В основном метод аналогии применим при решении геометрических задач (в том числе задач стереометрии по аналогии с планиметрическими).
Рассмотрим пример геометрической задачи, когда найти способ решения позволяет метод аналогии.
Задача 12. Зная стороны треугольника ABC, вычислить радиус r 
вневписанной окружности, касающейся стороны BC и продолжений сторон AB и AC.
Данная задача не является стандартной, поэтому сразу трудно определить алгоритм ее решения. Но возможно, что из рассмотрения вспомогательной задачи, сформулированной для исходной по аналогии, нетрудно будет найти способ решения исходной. Аналогичная ей может выглядеть следующим образом:
Зная стороны a, b, c треугольника ABC, вычислить радиус r вписанной окружности.
 |
Решение. 1. Соединим центр О вписанной окружности с вершинами треугольника ABC.
2. S = S 
+ S 
+ S 
(1)
3. Обозначим площадь треугольника ABC через S, тогда по формуле Герона
S = 
.
4. S = 
cr, S = br, S = ar.
5. Из (1) следует, что S = ( c+ b+ a )r = pr, откуда r = 
, или A
r = 
.BC
 |
Решение задачи К+1. 1. Соединим центр О 
вневписанной окружности с вершинами 
ABC.
2. S 
= S 
+ S 
– S 
(1).
3. Обозначим площадь треугольника ABC через S, тогда по формуле Герона
S = 
.
4. S 
= 
, S = 
, S 
= 
.
5. Из (1) первого следует, что S = ( c+ b - a )r =( p- a) r 
, откуда
r = 
или r = 
. Задача решена.
На данном примере наглядно показан прием аналогии решения задач, которым можно пользоваться, соблюдая следующие этапы:
a) подбор задачи, аналогичной исходной, т.е. такой, что у нее и исходной задачи сходные условия и сходные заключения. Вспомогательная задача конечно должна быть проще исходной или ее решение должно быть известно;
б) после решения вспомогательной задачи проводятся аналогичные рассуждения для решения исходной задачи.
4.2 Индукция
Индукция один из самых важных эвристических методов, поскольку рассмотрение частных случаев задачи вполне вероятно может привести решающего к методу решения задачи в общем случае. Подробнее – если задача трудная, то полезно попытаться выделить какой-либо простой ее частный случай, с которым нетрудно справиться. После этого следует перейти к другим, более сложным случаям, и так до тех пор, пока будет решена задача.
Соображения непрерывности”
В математике часто заключения об истинности или правдоподобии какого-то факта выводятся с помощью соображений непрерывности. Несмотря на то, что для учащихся школы строгое определение непрерывности сложно, наглядное представление о величинах, меняющихся непрерывно с течением времени имеет каждый (например, путь, величина угла и т.д.).
Отправляясь от таких наглядных представлений, можно дать математическое определение того, что значит, какая-то величина U менялась с течением времени непрерывно: это значит, что при любом выборе момента t 
в течение достаточно малого промежутка времени (t 
- h, t + h) значения этой величины отличались от ее значения в момент t меньше, чем наперед заданное допустимое отклонение d. Следует иметь ввиду, что допустимое отклонение d задается здесь заранее и может быть выбрано как угодно малым. Утверждается, что при любом таком выборе d можно в зависимости от этого d для каждого момента t подобрать настолько малый промежуток времени (t - h, t + h), чтобы значения величины U в любой момент из этого промежутка отличались от его значения в момент t меньше, чем на d. В конкретных случаях обычно бывает достаточно ясно, можно ли считать, что та или иная величина меняется непрерывно.
При решении задач особенно полезно бывает следующее интуитивно очевидное свойство непрерывно меняющейся величины: если какая-либо величина (например, длина, сумма углов, площадь и т.п.) менялись непрерывно в течение какого-либо отрезка времени и в начальный момент она была меньше постоянной величины а, а в конечный момент больше, чем а, то в какой-то промежуточный момент она была равна а.
Применение данного свойства хорошо иллюстрирует следующий пример.
Задача15. Легко догадаться, что уравнение 2 
=4х имеет корень х=4. Имеет ли оно еще хотя бы один корень?
Решение. Рассмотрим “поведение ” этой функции на отрезке [ 0; 1].
При х= 0 2 
- 4х > 0, а при х= 1 2 
- 4х < 0, поэтому найдется такое промежуточное значение х, что 2 
- 4х = 0.
Заключение
В работе на основе изучения структуры решения математической задачи был выделен этап поиска решения задачи, который в случае решения нестандартной задачи выполняется, если используется применение эвристических приемов решения задачи.
Такое условие привело к необходимости изучения понятия эвристического метода и систем эвристических приемов решения математических задач Л.М. Фридмана и М.Б. Балка. Изучение и сравнение данных систем потребовало их изложения с приведением примеров математических задач с решениями в роли иллюстраций к особенностям каждой системы.
Литература
1. Балк Г.Д. О применении эвристических приемов в школьном курсе математики // Математика в школе. – 1969. – №5. – С.21–28.
2. Балк М.Б., Балк Г.Д. О привитии школьникам эвристического мышления // Математика в школе. – 1985. – №2. – С.55 – 60.
3. Большая Советская Энциклопедия, 1978. Том 29.
4. Пойа Д. Как решать задачу. – Львов: журнал “Квантор”,1991.
5. Фридман Л.М. Теоретические основы методики обучения математике в школе: Пособие для учителей, методистов и педагогических высших учебных заведений. – М.: Флинта, 1998.
6. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Книга для учащихся старших классов средней школы. – М.: Просвещение, 1989.
7. Пушкин В.Н. Эвристика – наука о творческом мышлении. – М.: Политиздат, 1967.
Кафедра Методики преподавания математики
КУРСОВАЯ РАБОТА
Эвристические методы поиска
Способа решения задач
Выполнила студентка
математического факультета
4 курса группы М - 43
Гагаринова Ольга
Научный руководитель:
ассистент Шилова З.В.
Киров 2003
СОДЕРЖАНИЕ
Введение.
1. Структура процесса решения задач. Поиск способа решения задач.
2. Эвристический метод решения задач, его понятие.
3. Система эвристических методов Л.М. Фридмана/
3.1 Метод разбиения задачи на подзадачи.
3.2 Метод преобразования задачи.
3.3 Метод моделирования.
3.4 Метод вспомогательных элементов.
4. Система эвристических методов М.Б. Балка/
4.1 Аналогия.
4.2. Индукция.
4.3 Предельный случай.
4.4 Соображения непрерывности.
Заключение.
ВВЕДЕНИЕ
В настоящее время во всех сферах человеческой жизнедеятельности – науке, технике, народном хозяйстве и др. – возникают вопросы, проблемы нестандартного характера, разрешение которых зачастую невозможно осуществить посредством стандартных приемов, методов, ставших уже привычными. Условия жизни ставят всех нас перед необходимостью полного применения своих способностей и психо-физических ресурсов для решения сложных, нестандартных задач, что в итоге приводит к психическому и физическому перенапряжению, истощению жизненных сил. Такое положение вещей приводит нас к необходимости научиться решать подобные задачи с наименьшим объемом затрат. Известный психолог XX века В.Н.Пушкин по этому поводу высказывал свое мнение: “Человек должен совершить некоторую совокупность действий, решить ту или иную задачу, однако наличные условия не подсказывают ему способа решения этой задачи… . Чтобы найти выход из подобной ситуации, человеку необходимо создать новую, не имевшуюся у него ранее стратегию деятельности, т.е. совершить акт творчества”. В итоге встает вопрос об универсальном методе действий, который включает в себя продуктивный способ мышления, характер (направленность) действий, позволяющем разрешить поставленную проблему.
В науке давно известен и до сих пор совершенствуется такой метод. Название его – эвристический метод. Эвристическая деятельность является “разновидностью человеческого мышления, которая создает новую систему действий или открывает ранее неизвестные закономерности …”[7, стр.6].
С точки зрения американского математика Дердье Пойа цель эвристики – исследовать правила и методы, ведущие к открытиям и изобретениям.
Однако, по мнению того же В.Н.Пушкина, эвристика-наука исследует закономерности эвристической как творческой деятельности человека.
В виду этого несложно усмотреть, что эвристика, в частности, эвристические приемы, методы оказывают достаточно сильное влияние на развитие творческих способностей, и, что не менее важно, на развитие творческого мышления.
Поэтому оказывается очень важным прививать новому поколению эвристические знания, а значит, обучать в школе эвристическому мышлению. Лучше всего это можно осуществить на уроках математики, изучая “общие приемы поиска решения задач, пригодных к любым, в том числе и “нетиповым”, нестандартным задачам”, иначе, обучая владению эвристическими приемами (методами) решения математических задач.
В связи с этим, целью данной работы является изучение эвристических методов решения математических задач.
В процессе выполнения работы необходимо было решить следующие задачи:
● во-первых, для осознания сути решения математической задачи важно было изучить структуру решения задачи;
● было рассмотрено понятие эвристического метода решения задачи и трактовка его особенностей с различных позиций;
● далее нужно было изучить соответствующие эвристические системы методов решения задач русских математиков Л.М. Фридмана и М.Б. Балка;
● в работе излагаются обе системы эвристических методов, причем система методов Л.М. Фридмана иллюстрируется примерами задач, подобранными самостоятельно;
● кроме того, в работе сравниваются две данные системы эвристических методов на основе выделения особенностей каждой.
Дата: 2019-12-10, просмотров: 212.
