Постановка задачи:
ДУЧП:
Граничные условия Дирихле.
Идеи построения приближенного решения краевой задачи для ДУЧП:
1. Это переход от значений искомой функции на непрерывном множестве точек (область 
) к значениям этой функции на дискретном множестве точек.
Для этого область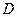 
покрывается сеткой (проще всего прямоугольной, но может быть из треугольных, шестиугольных ячеек) и вычисляются значения искомой функции только в узлах этой сетки.
Узлы сетки нужно разделить на внутренние и граничные и далее ставить задачу вычисления искомой функции во внутренних узлах, зная значения функции в граничных узлах.
При этом искажение границы области 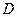обязательно будет (если 
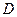не прямоугольная), но его можно уменьшать за счет размеров ячеек сетки.
2. Это замена ДУЧП на конечно-разностное уравнение. Для этого используется определение производной.
Геометрически 
(для малых 
)
Из теоремы математического анализа о конечных пределах:
Таким образом, из определения и геометрического смысла производной следует, что значение производной в некоторой точке можно посчитать как отношение конечных разностей, т.е. как отношение приращения функции к приращению ее аргумента.
Применим эту идею к произвольному узлу прямоугольной сетки.
Введем обозначения для узлов:
Узел 
- это точка с координатами 
, где
Для каждого из внутренних узлов будем заменять частные производные на отношение конечных разностей.
Таким образом, 
Аналогично:
Аналогично:
Пересчитав все частные производные, которые нужны для исходного ДУЧП через конечные разности, фиксируем, так называемую, конечно-разностную схему, т.е. схему, показывающую, какие узлы будут задействованы, если работать с ДУЧП в фиксированном узле 
. Так для ДУЧП Лапласа получилась конечно-разностная схема в виде креста. Подставляем все пересчитанные частные производные в ДУЧП и получаем конечно-разностное уравнение в узле 
.
Если такое конечно-разностное уравнение 
записать в каждом внутреннем узле, то мы получим систему, содержащую 
алгебраических уравнений относительно такого же количества неизвестных.
Система будет алгебраической, линейной по всем неизвестным, неоднородной (т.к. в эту систему войдут значения функции 
в граничных узлах, поэтому они будут перенесены в правую часть уравнения). Такая система может быть решена методом Гаусса (возможно, с какой-либо модификацией метода).
Таким образом, решение краевой задачи для ДУЧП методом сеток сводится к решению системы линейных уравнений относительно значений искомой функции во внутренних узлах прямоугольной сетки, покрывающей область 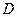. При этом матрица системы содержит большое количество нулей (в общем случае является трехдиагональной матрицей), поэтому организовать метод Гаусса для решения этой системы всегда можно так, чтобы решение системы получалось практически точным.
Характеристика и особенности метода конечных разностей.
1. Границы применимости метода:
1) По ДУЧП:
По однородности ДУ ограничений нет.
По линейности – линейное ДУЧП сводится к системе линейных алгебраических (……………), нелинейное – к нелинейной системе.
2) По области, которой ищется решение.
Ограничений по области нет.
3) По постановке граничных и начальных условий:
Ограничений нет, хотя для граничных условий Неймана есть некоторая особенность реализации метода.
4) По виду функций, задающих начальные и граничные условия.
Ограничений нет.
2. Сходимость метода конечных разностей.
Метод конечных разностей хорошо сходится только для ДУЧП Лапласа, т.е. для ДУЧП Лапласа гарантировано, что, если делать сетку, покрывающую область 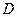с более мелкими ячейками, то решение методом сеток будет приближаться к точному.
Для уравнения теплопроводности есть достаточное условие сходимости, оно связывает величину разбиения по оси Ox и по оси Oy.
, 
из ДУЧП теплопроводности.
Для волнового уравнения метод сеток будет гарантированно сходиться, если использовать явную конечно-разностную схему (тогда при 
и 
).
Все эти условия являются достаточными.
3. Понятия о явной и неявной конечно-разностных схемах.
Конечно-разностная схема называется неявной, если вместо ДУЧП получилась система ЛДУ, в которой все неизвестные находятся не последовательно, а в результате общего решения системы.
Такая схема получается для ДУЧП Лапласа.
Явная конечно-разностная схема получается, если ДУЧП сводится к такому конечно-разностному уравнению, из которого понятно, что 
в узлах сетки можно находить последовательно, не решая систему.
Например, для ДУЧП теплопроводности:
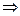Конечно-разностная схема получится в виде перевернутой буквы Т.
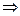Конечно-разностное уравнение, записанное для всех точек 
, где
Получается возможность вычислять значения 
во внутренних узлах по слоям.
Из конечно-разностного уравнения для узла (0,1) находим 
, для узла (0,2) находим 
. Отсюда известны все 
для второго слоя. Далее, записывая конечно-разностное уравнение для 1 слоя, получим все 
для второго слоя. Продвигаясь по слоям, нужно вести вычисления до тех пор, пока не получим слой с числами установившегося процесса ( 
с точностью 
).
Рассмотрим идею перехода к явной конечно-разностной схеме для волнового уравнения.
Конечно-разностная схема будет получаться в виде креста записав конечно-разностное уравнение во всех узлах 
(внутренних) области 
.
Получим систему ЛДУ, т.е. неявную (***************) и при этом в эту систему не будет входить второе начальное условие:
(***********)
Если это начальное условие учесть как важное для решения задачи, то есть возможность перейти на явную схему, используя фиктивный слой с номером 
.
Для этого запишем через граничные разности с шагом назад:
, где
- это значение в точках 
- это значение на фиктивном слое с номером 
.
Из равенства 
находим 
Тогда записывать конечно-разностное уравнение надо, начиная с узла (1,0). В этом уравнении будут неизвестными 
найдем 
. Далее аналогично, записав уравнение в точке (2,0), найдем 
. Таким образом, станут известны значения на 1 слое. Далее, аналогично.
Конечно-разностная схема стала явной, а заодно учитывает все начальные условия.
4. Как учесть граничные условия Неймана методом сеток:
При этом граничные условия Неймана записываются через граничные разности:
- пересчет условий Неймана на условия Дирихле при 
.
- пересчет граничного условия Неймана на условие Дирихле при 
.
Реализация метода конечных разностей в курсовой работе.
1. Численно просчитать во всех внутренних узлах, выбрав для этого сетку 
.
Результаты вычислений оформить в виде таблицы значений функции 
во всех узлах.
2. Сравнить значения , вычисленные по приближенному и точному методам:
Абсолютную и относительные погрешности вывести таблицей, в которой указать 
с max значением погрешностей.
3. Сделать выводы о приближенном решении задачи.
Дата: 2019-12-10, просмотров: 214.
