1. Постановка матмодели задачи
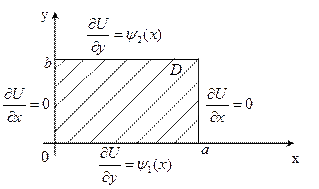
ДУЧП: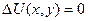 
Граничные условия:
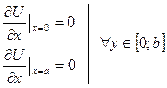
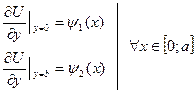
Согласование граничных условий в угловых точках области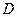 
не требуется, т.к. в каждой из этих точек 
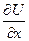и 
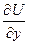могу т принимать разные значения.
2. Решение задачи методом Фурье.
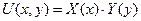1. 
(1)
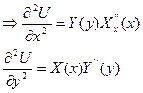
ДУЧП: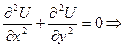 
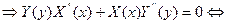
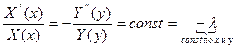
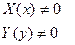, т.к. ищем нетривиальные решения задачи.
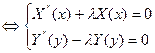(2)
2. Нулевые граничные условия:
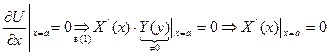
3. Задача Штурма-Лиувилля
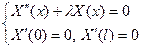(3)
Требуется найти собственные числа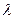 
, при которых задача (3) имеет нетривиальные решения, называемые собственными функциями задачи Штурма-Лиувилля.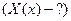 
ДУ из (3):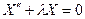 
- обыкновенное ДУ II порядка, линейное, однородное, с постоянными коэффициентами.
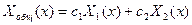, где
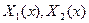- ФСЧР.
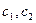- константы по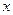 
Характеристическое уравнение:
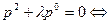
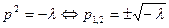
1) случай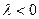 
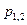- действительные различные числа противоположных знаков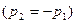 
ФСЧР: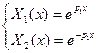 
. 
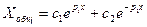
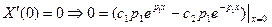
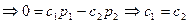
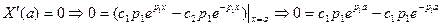
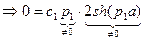
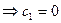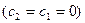
Таким образом, при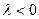 
решением задачи (3) является только функция 
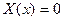(тривиальное решение), значит, при 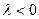задача Штурма-Лиувилля решений не имеет.
2) случай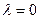 
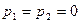- случай равных действительных корней.
ФСЧР: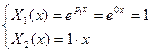 
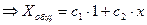
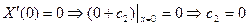
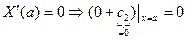- удовлетворяет тождественно
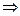Решением задачи (3) является 
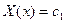- нетривиальное решение задачи (3) при 
,
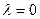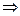
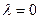- является одним из собственных чисел задачи Штурма-Лиувилля.
3) случай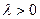 
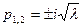- комплексно-сопряженные корни
ФСЧР: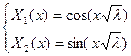 
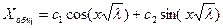
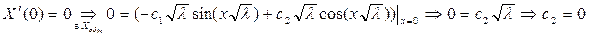
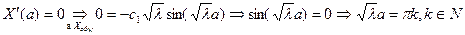
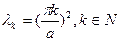
Таким образом, собственными числами задачи Штурма-Лиувилля являются:
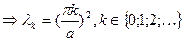(4)
Собственными функциями задачи Штурма-Лиувилля являются
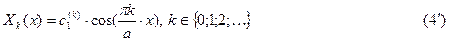
Задача Штурма-Лиувилля разрешена.
4. 
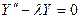- обыкновенное ДУ II порядка, однородное, линейное, с постоянными коэффициентами, где 
.
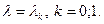Характеристическое уравнение:
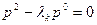
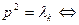
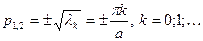- действительные различные корни при 
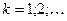или действительные равные корни при 
.
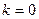ФСЧР: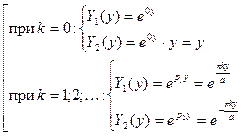 
Общее решение:
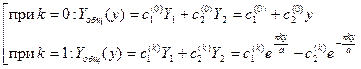
При решении уравнения Лапласа в качестве ФСЧР для второго обыкновенного ДУ системы (2) удобно взять гиперболические функции, основываясь на свойстве решений обыкновенных линейных однородных ДУ II порядка:
Есл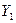и 
и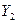 
- решения ЛОДУ, то 
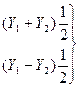тоже решения этого ЛОДУ
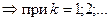лучше взять
ФСЧР: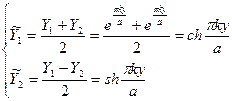 
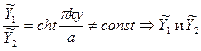являются линейно-независимыми, и, следовательно, годятся для ФСЧР.
Таким образом, с учетом этого замечания, решение второго ДУ из системы (2) получаем в следующем виде:
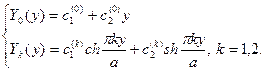(5)
5. Перемножением функци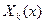й 
и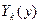 
находим счетное множество функций 
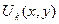и составляем из них функциональный ряд:
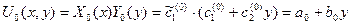
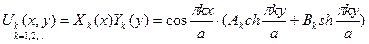
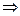Составив ряд, мы предположим его сходимость:
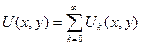
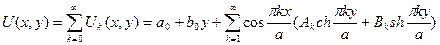(6)
Для этого ряда предполагается равномерная сходимость для всех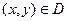 
.
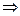Подстановку граничных значений и дифференцирование ряда можно осуществить почленно.
Так составленная функция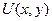 
удовлетворяет граничным условиям на двух противоположных сторонах и ДУЧП. Для определения коэффициентов 
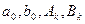будем удовлетворять (двум) другим граничным условиям на двух других противоположных сторонах.
6. Определение коэффициентов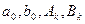
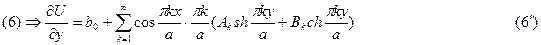
Граничные условия:
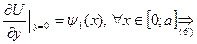
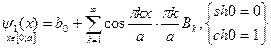
Это равенство представляет собой разложение в ряд Фурье по косинусам функции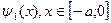 
, продолженной четным образом на промежуток 
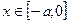и периодически с 
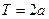на всю числовую ось.
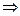коэффициенты этого разложения могут быть вычислены по формулам Фурье:
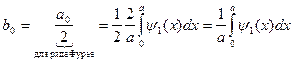(7)
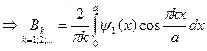(8)
Другое граничное ненулевое условие:
Это разложение в ряд Фурье по косинусам функции 
, продолженной четным образом на 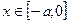и периодически с 
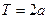на всю числовую ось.
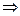коэффициенты можно вычислять по формулам Фурье:
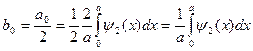
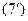
Надо согласовать (7) и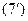 
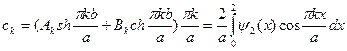
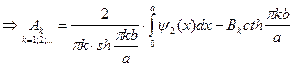(9)
Особенности в определении коэффициентов:
1. в результате решения задачи не определился коэффициент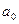 
в формуле (6).
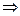искомая функция 
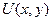будет определена с точностью до постоянного слагаемого, и это хорошо согласуется с условиями задачи (и ДУЧП и все граничные условия будут хорошо удовлетворять, если 
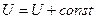). При численном исследовании решения можно положить 
.
2. Для коэффициента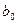 
получились 2 формулы (7) и 
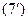, и отсюда следует:
Это равенство описывает согласование начальных условий и физически означает, например, в задаче стационарной теплопроводности в области 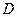, что тепловой поток через границу 
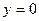должен быть равным тепловому потоку через границу 
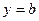(в противном случае процесс теплопроводности не будет установившимся).
Тепловой поток – количество тепла, проходящее через границы.
Таким образом, решение задачи Неймана для уравнения Лапласа в прямоугольной области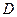 
получено в виде уравнения (6), коэффициенты которого нужно считать по формулам (7), (8), (9).
Дата: 2019-12-10, просмотров: 279.
