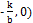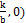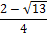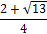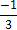Линейные и квадратичные зависимости, функция/х/ и связанные с ними уравнения и неравенства
Дипломная работа по алгебре
22.06.2008
Сурскова Т.А.
СОДЕРЖАНИЕ
Введение
Глава 1. Линейная зависимость и связанные с ней уравнения и неравенства
1.1 Линейная функция
1.2 Линейные уравнения и неравенства
1.3 Решение линейных неравенств
Глава 2. Квадратичная зависимость и связанные с ней уравнения и неравенства
2.1 Квадратный трехчлен
2.2 Корни квадратного трехчлена
2.3 Зависимость расположения графика функции квадратного трехчлена от а, D
2.4 Решение квадратных неравенств
2.5 Разложение квадратного трехчлена на линейные множители
2.6 Выделение полного квадрата, как метод решения некоторых нестандартных задач
2.7 Равносильность и следствие в задачах с квадратным трехчленом
Глава 3. Функция  и связанные с ней уравнения и неравенства
и связанные с ней уравнения и неравенства
3.1 Определение и свойства функции 
3.2 Уравнения и неравенства, содержащие модули
Заключение
Литература
Приложение
Введение
Актуальность исследования.
В настоящее время в научно-методической литературе и периодических изданиях активно обсуждается «качество» математических знаний, приобретаемых учащимися общеобразовательных школ. Методисты, учителя математики, студенты педагогических институтов задают себе один и тот же вопрос: «Почему многие ученики не чувствуют взаимосвязи между изучаемыми темами, не умеют применять пройденный теоретический материал к решению задач, нередко через несколько уроков теряя приобретённые умения, так и не ставшие навыками?»
Данная работа не даёт исчерпывающего ответа на этот сакраментальный вопрос. (Если такой ответ вообще существует.) Однако основные принципы этой работы и её задачи являются своеобразной альтернативой наиболее часто применяемой системе изложения математических сведений.
Изучение линейных и квадратичных зависимостей, функции |х| — всё чаще предлагаются абитуриентам на вступительных экзаменах самых различных ВУЗов. Но эти темы по-прежнему вызывают затруднения у многих старшеклассников. Предпринятая в данной работе попытка систематизировать и обобщить теоретический материал по этой теме (как входящий в рамки школьного курса, так и выходящий за его пределы) может стать примером системного подхода к курсу алгебры и упомянутой выше альтернативой простому нарешиванию задач.
Кроме качества приобретённых знаний, выпускнику современной школы жизненно необходимо умение мыслить самостоятельно. Современному молодому человеку необходимо умение жить в мире, где думать - не развлечение, а обязанность. Поэтому существенная часть данной работы посвящена квадратичной зависимости и уравнениям и неравенствам, связанными с ней. Данная тема позволяет развить познавательную активность, творческую самостоятельность учащихся, интуитивное мышление, умение рассуждать и спорить. Нельзя сказать, что методисты и педагоги-учёные обходили своим вниманием этот вопрос. Однако в данной теме всегда находится что-то новое и интересное, позволяющее находить нестандартное решение.
Опираясь на всё выше сказанное, сформулируем задачи исследования.
Задачи.
1. Обобщить и систематизировать сведения о линейных и квадратичных зависимостях и связанных с ними уравнениями и неравенствами.
2. Показать выделение полного квадрата, как метод решения некоторых нестандартных задач.
3. Показать эффективность применения данного метода к решению задач.
4. Проанализировать методико-педагогическую литературу по теме
« Линейные и квадратичные зависимости»
5. Выполнить подборку задач, для которых решение сводилось бы к линейным или квадратичным зависимостям.
Структура работы.
Работа состоит из введения, трёх глав, заключения и приложения, включает страниц машинописного текста и имеет список литературы из наименований.
Линейная функция
Определение. Функция, задаваемая формулой у = k ·х + b , называется линейной.
В школьной программе доказывается, что графиком линейной функции на плоскости является прямая, и обратно, что любая прямая на плоскости есть график некоторого линейного уравнения a· x + b · y + c = 0.
Уравнение у = k ·х + b называется уравнением прямой с угловым коэффициентом k
 | |||
 | |||
|


|
|
 | |||
| |||
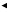
|

 |
|
|
|
|
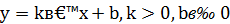
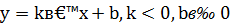
Приведенные выше два рисунка иллюстрируют связь параметров k и b с особенностями расположения прямой в декартовой системе координат. В частности, число k = tg α называется угловым коэффициентом прямой.
В данном случае  . Если k = 0, то
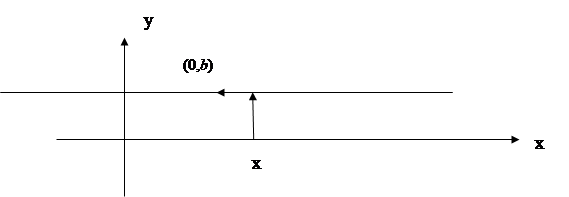
. Если k = 0, то  , линейная функция постоянна и задает прямую, параллельную оси ОХ и | проходящую через точку (0,b) на оси OY.
, линейная функция постоянна и задает прямую, параллельную оси ОХ и | проходящую через точку (0,b) на оси OY.
Перечислим основные свойства линейной функции.
1. Ее областью определения является множество R.
2. Если k  0 , то множеством значений линейной функции также является множество R, если k = 0, то множество значений — одноточечное множество b .
0 , то множеством значений линейной функции также является множество R, если k = 0, то множество значений — одноточечное множество b .
3. Если k > 0, то 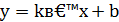 - монотонно возрастающая функция на R, если k < 0, то
- монотонно возрастающая функция на R, если k < 0, то 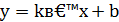 - монотонно убывает на R.
- монотонно убывает на R.
4. Если b = 0, то 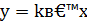 - нечетная функция, у = b - четная функция; если же
- нечетная функция, у = b - четная функция; если же 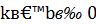 , то
, то 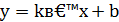 не является четной или нечетной функцией.
не является четной или нечетной функцией.
Рассмотренные выше случаи не позволяют задать прямую, параллельную оси OY. Поэтому условимся, что уравнение х=х0 задает
множество всех точек вида (х0, у), где у 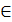 R, то есть задает прямую
R, то есть задает прямую
параллельную оси OY и проходящую че рез точку (хо, 0) на оси ОХ.
Чтобы построить прямую, задаваемую уравнением  , достаточно найти две точки (х0, у0) и (х1, у1), удовлетворяющие этому уравнению: у0 = k
, достаточно найти две точки (х0, у0) и (х1, у1), удовлетворяющие этому уравнению: у0 = k 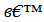 х0 + b ; у1 = k
х0 + b ; у1 = k 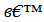 х1 + b и провести через них искомую прямую.
х1 + b и провести через них искомую прямую.
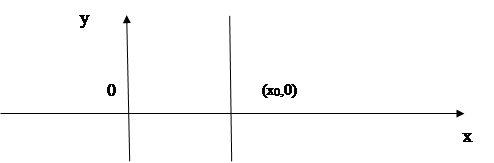
Решение линейных неравенств
Сразу же выпишем решения в виде готового правила:
1) а  х > b , если a > 0, то x >
х > b , если a > 0, то x > 
если a < 0, то x < 
если a = 0 и b < 0, то x – любое число,
если a = 0 и b  0, то решений нет.
0, то решений нет.
2) а  х < b , если a > 0, то x <
х < b , если a > 0, то x < 
если a < 0, то x > 
если a = 0 и b  0, то решений нет,
0, то решений нет,
если a = 0 и b >0, то x – любое число.
Всегда полезно помнить следующее основное правило:
При умножении или делении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.
При умножении или делении обеих частей неравенства на положительное число знак неравенства не изменяется.
Квадратный трехчлен
Определение. Квадратным трехчленом называется функция 
Выделение полного квадрата путем тождественных преобразований.

Иначе можно записать в виде:

Пример 1.

Пример 2.

Определение. Число  называется дискриминантом квадратного трехчлена
называется дискриминантом квадратного трехчлена 
Корни квадратного трехчлена
Нужно найти корни уравнения

Выделив полный квадрат, получим формулу (*), откуда


Мы должны рассмотреть три случая:
1)  , тогда
, тогда


В этом случае уравнение 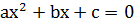 имеет два различных корня:
имеет два различных корня:

2)  , тогда
, тогда 
в силу (*), то есть  - два совпадающих корня.
- два совпадающих корня.
3)  ,
,
Тогда 
не имеет вещественных корней, так как

Итак, доказана теорема:
Теорема 1. Пусть имеется уравнение 
 если
если
1)  , то уравнение не имеет вещественных решений.
, то уравнение не имеет вещественных решений.
2)  , то уравнение имеет два равных корня
, то уравнение имеет два равных корня 
3)  , то уравнение имеет два различных корня
, то уравнение имеет два различных корня

Замечание: если 

В этом случае корни удобно находить по формуле

Теорема 2. Если а > 0, то функция  монотонно убывает для
монотонно убывает для  и монотонно возрастает для
и монотонно возрастает для 
Доказательство теоремы:
Пусть  (1),
(1),
где  произвольные фиксированные числа, тогда из (1) получаем
произвольные фиксированные числа, тогда из (1) получаем




а это по (**) есть  , что требовалось доказать.
, что требовалось доказать.
1) В этом рассуждении использовано монотонное возрастание функции  на множестве
на множестве 
2) Докажите, что функция  монотонно возрастает на множестве
монотонно возрастает на множестве 
Аналогично доказывается монотонное возрастание функции  на
на 
Теорема 3. Если а < 0, то функция  монотонно возрастает для
монотонно возрастает для  и монотонно убывает для
и монотонно убывает для 
Доказательство теоремы аналогично доказательству теоремы 2.
Следствие.
Если а > 0, то  для любого х
для любого х 
Если а < 0, то  для любого х
для любого х 
При а > 0 
При а < 0 
min и max достигаются при x =  .
.
Точка  называется вершиной параболы.
называется вершиной параболы.
Теорема 4.
1) Если D > 0, то 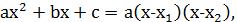

2) Если D = 0, то 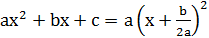 .
.
3) Если D < 0, то 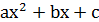 нельзя разложить на линейные множители, используя в качестве коэффициентов этих линейных множителей вещественные числа.
нельзя разложить на линейные множители, используя в качестве коэффициентов этих линейных множителей вещественные числа.
Пример 1. 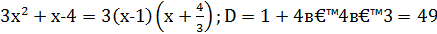
Пример 2. 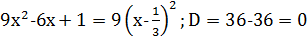
Пример 3. 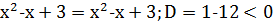 .
.
Укажем и другие связи между корнями и коэффициентами квадратного трехчлена.
Теорема 5. (Виета)
Если 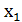 ,
, 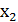 - вещественные корни уравнения
- вещественные корни уравнения 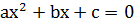 , то
, то
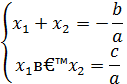
Теорема 6. (Обратная теорема Виета)
Если 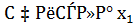 ,
, 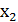 удовлетворяют условиям системы:
удовлетворяют условиям системы:

то 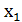 ,
, 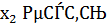 корни уравнения
корни уравнения 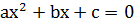 .
.
Часто встречаются задачи, в которых требуется выяснить взаимное расположение какого-либо числа и корней квадратного трехчлена на числовой оси.
Следующая теорема позволяет существенно упростить решение подобного рода задач. Отметим, что для уменьшения числа разбираемых различных случаев мы переходим к рассмотрению приведенного квадратного уравнения, которое получается после деления всех коэффициентов уравнения на старший коэффициент a.
Теорема 7.
Пусть 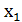 ,
, 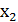 - вещественные корни уравнения
- вещественные корни уравнения 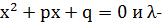 число.
число.
| Для того, чтобы | Необходимо и достаточно |
I. 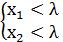
| 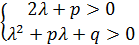
|
II. 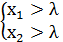
| 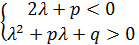
|
III. 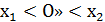
| 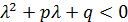
|
Место для формулы.
Докажем случай 1.
Необходимость.
Пусть 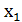 ,
, 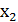 - вещественные корни уравнения
- вещественные корни уравнения 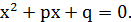
Если 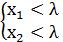 , то необходимо выполняются условия
, то необходимо выполняются условия
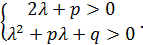
Доказательство.
Так как по условию
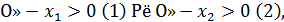
то сложив (1) и (2) получим 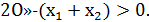 По теореме Виета
По теореме Виета 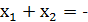 p, то есть
p, то есть 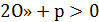 , что и требовалось доказать.
, что и требовалось доказать.
Перемножив (1) и (2), получим
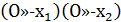 >0
>0 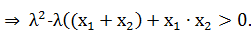
Воспользовавшись теоремой Виета:
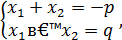
получим 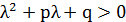 , что и требовалось доказать.
, что и требовалось доказать.
Достаточность.
Пусть 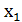 ,
, 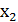 - вещественные корни уравнения
- вещественные корни уравнения 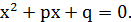
Для того, чтобы оба корня были меньше числа 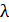 , достаточно, чтобы выполнялась следующая система неравенств:
, достаточно, чтобы выполнялась следующая система неравенств:
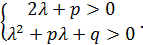
Доказательство.
По условию, справедлива система:
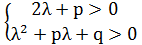 (1)
(1)
Вновь воспользуемся теоремой Виета
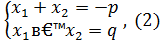
тогда система (1) примет вид:
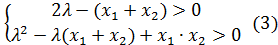
Переписав систему (3) в другом виде, получим систему (4):
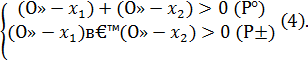
Неравенство (б) означает, что числа 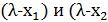 ) имеют одинаковые знаки, а неравенство (а), что оба эти числа положительны, то есть
) имеют одинаковые знаки, а неравенство (а), что оба эти числа положительны, то есть
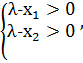 иначе говоря
иначе говоря 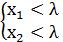 , что и требовалось доказать.
, что и требовалось доказать.
Задачи
Обозначим через 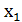 ,
, 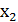 корни квадратного трехчлена (a-1)
корни квадратного трехчлена (a-1) 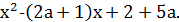 Найти все а, при которых оба корня больше 1.
Найти все а, при которых оба корня больше 1.
Решение.
а) Если а=1, то уравнение -3x + 7 = 0 имеет только один корень, поэтому 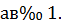
б) При 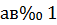 воспользуемся пунктом II теоремы 7, который позволяет сразу записать:
воспользуемся пунктом II теоремы 7, который позволяет сразу записать:
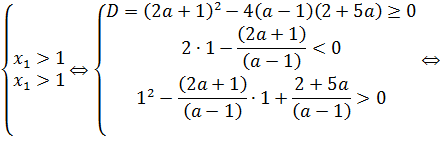
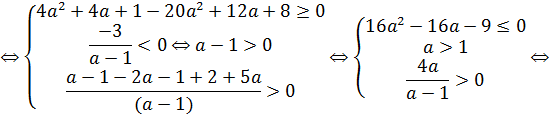
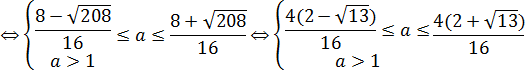
 | |||||||||
|
|
| |||||||
Ответ.  .
.
2. Найти все значения 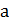 , при которых корни уравнения
, при которых корни уравнения 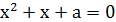 больше
больше 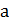 .
.
Решение.
Воспользовавшись пунктом II теоремы 7 получаем:
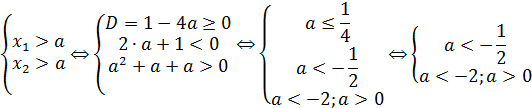

Ответ. a < -2.
3. Найти все значения 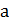 , при которых оба корня квадратного уравнения
, при которых оба корня квадратного уравнения
 будут меньше 1.
будут меньше 1.
Решение.
Уравнение будет квадратным только если 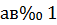 . В этом случае оно равносильно уравнению:
. В этом случае оно равносильно уравнению:
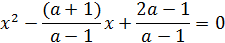
Согласно пункту 1 теоремы 7 получаем, что
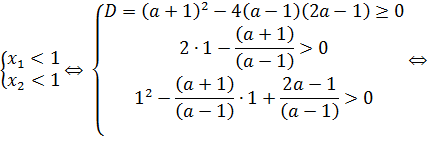
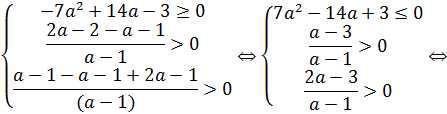
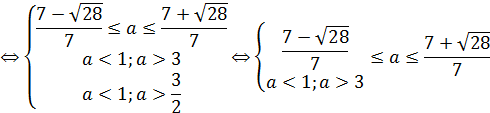
 | ||||||||||||||
 | ||||||||||||||
|
| |||||||||||||
| ||||||||||||||
 | ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
|










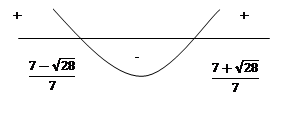
Ответ. 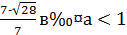 .
.
Иногда применение теоремы 7 вызывает трудности, так как возникают неравенства третьей или более высокой степени. Тогда, скорее всего, можно выражения для корней исходного квадратного трехчлена получить в виде рациональных функций параметра.
Иными словами:
Если применение теоремы 7, вызывает алгебраические трудности, стоит проверить, не является ли дискриминант рассматриваемого квадратного уравнения полным квадратом. Если дискриминант является полным квадратом, то нужно попытаться выписать выражения для корней и продолжить решение задачи.
4. При каких значениях а все корни уравнения
3a 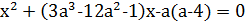 удовлетворяют условию
удовлетворяют условию 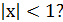
1) Заметим, что если 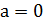 , то уравнение имеет единственный корень
, то уравнение имеет единственный корень 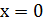 , и число 0 удовлетворяет условию задачи.
, и число 0 удовлетворяет условию задачи.
2) Если 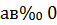 , то
, то 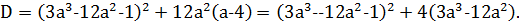
Заменим  , тогда
, тогда
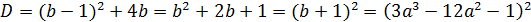
- данное выражение есть полный квадрат! Теперь легко вычислить:

Условие задачи будет выполнено, если справедлива система:
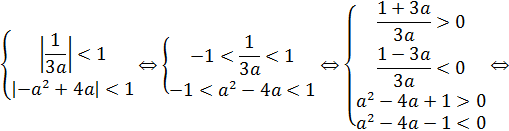
 | ||||||||||||
| ||||||||||||
 | ||||||||||||
|
| |||||||||||
 | ||||||||||||
|
|
|

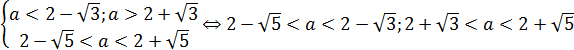
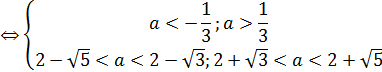
Сравним числа из промежуточных ответов:
пусть 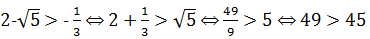 верно;
верно;
пусть 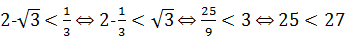 верно.
верно.
 |
Пересечение ответов является множество:
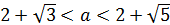
Ответ. 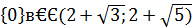
Линейные и квадратичные зависимости, функция/х/ и связанные с ними уравнения и неравенства
Дипломная работа по алгебре
22.06.2008
Сурскова Т.А.
СОДЕРЖАНИЕ
Введение
Глава 1. Линейная зависимость и связанные с ней уравнения и неравенства
1.1 Линейная функция
1.2 Линейные уравнения и неравенства
1.3 Решение линейных неравенств
Глава 2. Квадратичная зависимость и связанные с ней уравнения и неравенства
2.1 Квадратный трехчлен
2.2 Корни квадратного трехчлена
2.3 Зависимость расположения графика функции квадратного трехчлена от а, D
2.4 Решение квадратных неравенств
2.5 Разложение квадратного трехчлена на линейные множители
2.6 Выделение полного квадрата, как метод решения некоторых нестандартных задач
2.7 Равносильность и следствие в задачах с квадратным трехчленом
Глава 3. Функция  и связанные с ней уравнения и неравенства
и связанные с ней уравнения и неравенства
3.1 Определение и свойства функции 
3.2 Уравнения и неравенства, содержащие модули
Заключение
Литература
Приложение
Введение
Актуальность исследования.
В настоящее время в научно-методической литературе и периодических изданиях активно обсуждается «качество» математических знаний, приобретаемых учащимися общеобразовательных школ. Методисты, учителя математики, студенты педагогических институтов задают себе один и тот же вопрос: «Почему многие ученики не чувствуют взаимосвязи между изучаемыми темами, не умеют применять пройденный теоретический материал к решению задач, нередко через несколько уроков теряя приобретённые умения, так и не ставшие навыками?»
Данная работа не даёт исчерпывающего ответа на этот сакраментальный вопрос. (Если такой ответ вообще существует.) Однако основные принципы этой работы и её задачи являются своеобразной альтернативой наиболее часто применяемой системе изложения математических сведений.
Изучение линейных и квадратичных зависимостей, функции |х| — всё чаще предлагаются абитуриентам на вступительных экзаменах самых различных ВУЗов. Но эти темы по-прежнему вызывают затруднения у многих старшеклассников. Предпринятая в данной работе попытка систематизировать и обобщить теоретический материал по этой теме (как входящий в рамки школьного курса, так и выходящий за его пределы) может стать примером системного подхода к курсу алгебры и упомянутой выше альтернативой простому нарешиванию задач.
Кроме качества приобретённых знаний, выпускнику современной школы жизненно необходимо умение мыслить самостоятельно. Современному молодому человеку необходимо умение жить в мире, где думать - не развлечение, а обязанность. Поэтому существенная часть данной работы посвящена квадратичной зависимости и уравнениям и неравенствам, связанными с ней. Данная тема позволяет развить познавательную активность, творческую самостоятельность учащихся, интуитивное мышление, умение рассуждать и спорить. Нельзя сказать, что методисты и педагоги-учёные обходили своим вниманием этот вопрос. Однако в данной теме всегда находится что-то новое и интересное, позволяющее находить нестандартное решение.
Опираясь на всё выше сказанное, сформулируем задачи исследования.
Задачи.
1. Обобщить и систематизировать сведения о линейных и квадратичных зависимостях и связанных с ними уравнениями и неравенствами.
2. Показать выделение полного квадрата, как метод решения некоторых нестандартных задач.
3. Показать эффективность применения данного метода к решению задач.
4. Проанализировать методико-педагогическую литературу по теме
« Линейные и квадратичные зависимости»
5. Выполнить подборку задач, для которых решение сводилось бы к линейным или квадратичным зависимостям.
Дата: 2019-12-10, просмотров: 247.