Астраханский Государственный Педагогический Университет
Бакалаврская работа
Студентки IV курса физико–математического факультета
Ночевной Светланы Павловны
Кафедра:
Математического анализа
Тема:
Основные понятия дифференциального исчисления и история их развития
Научный руководитель
ст. преподаватель
Пономарёва Н.Г.
Астрахань
Г.
План.
1. Основные понятия дифференциального исчисления функций одной переменной.
1.1. Определение производной и её геометрический смысл.
1.2. Дифференциальные функции. Определение дифференциала.
1.3. Инвариантность формы первого дифференциала.
1.4. Дифференциал суммы, произведения и частного.
1.5. Геометрическая интерпретация дифференциала.
2. Основные понятия интегрального исчисления функций одной переменной.
2.1. Первообразная функция и неопределённый интеграл.
2.2. Геометрический смысл неопределённого интеграла.
2.3. Основные свойства неопределённого интеграла.
2.4. Метод непосредственного интегрирования.
2.5. Метод замены переменной (способ подстановки).
2.6. Интегрирование по частям.
2.7. Определённый интеграл как предел интегральной суммы.
2.8. Основные свойства определённого интеграла.
2.9. Геометрический смысл определённого интеграла.
2.10. Теорема Ньютона–Лейбница.
2.11. Формула Ньютона–Лейбница.
2.12. Замены переменных в определённых интегралах.
2.13. Интегрирование по частям.
3. Исторические сведения о возникновении и развитии основных понятий.
3.1. Происхождение понятия определённого интеграла и инфинитезимальные методы Архимеда.
3.2. От Архимеда к Кеплеру и Кавальери.
3.3. Теорема Паскаля.
3.4. «О глубокой геометрии» Лейбница.
3.5. «Метод флюксий» Ньютона.
3.6. Дифференциальные методы.
Цель работы: «Изучить основные понятия дифференциального и интегрального исчислений и ознакомиться с историей их развития».
Основные понятия дифференциального исчисления функций одной переменной.
Дифференциал суммы, произведения и частного.
Из теорем о производных суммы, произведения и частного можно получить аналогичные формулы для дифференциалов суммы, произведения и частного. Пусть и и J — функции от х:
и = f(х), J = j(х),
имеющие непрерывные частные производные.
Если положить у = и + J,
то у’х = и’х + J’х,
откуда у’х dх = и’х dх + J’хdх,
следовательно dу = dи + dJ,
то есть d(и + J) = dи + dJ.
Аналогично dси = сdи,
где с – постоянное число;
|
|
d ( ) = .
Замечание. На практике часто бывает выгоднее оперировать дифференциалами, а потом делением на дифференциал независимой переменной переходить к производной.
Основные понятия интегрального исчисления функций одной переменной.
Геометрический смысл неопределённого интеграла.
Пусть задан неопределённый интеграл F(х) + С для функции f(х) в некотором интервале. При фиксированном значении С = С1 получим конкретную функцию у1 = F(х) + С1, для которой можно построить график; его называют интегральной кривой. Изменив значение С и положив С = С2, получим другую первообразную функцию С соответствующей новой интегральной кривой.
Аналогично можно построить график любой первообразной функции. Следовательно, выражение у = F(х) + С можно рассматривать как уравнение семейства интегральных кривых неопределённого интеграла F(х) + С. Величина С является параметром этого семейства – каждому конкретному значению С соответствует единственная интегральная кривая в семействе. Интегральную кривую, соответствующую значению параметра С2, можно получить из интегральной кривой, соответствующей значению параметра С1, параллельным сдвигом в направлении оси Оу на величину /С2 – С1/. На рис. 3 изображён неопределённый интеграл х2 + С от функции f(х) = 2х, то есть, семейства парабол.
Интегрирование по частям.
Допустим, что u, v – функции переменной х, непрерывные и имеющие производные в интервале (а,в). имеем тогда
(uv)’ = uv’ + vu’
так что uv’ = (uv)’ – vu’
|
|
Если оба интеграла существуют.
|
|
udv = uv – vdu. (2)
|
|
1) J = хехdх.
|
v = ехdх = ех
Следовательно,
J = хех – ехdх = хех – ех + С.
|
Положим, u = ln х, dи = dх/х
|
|
J = х ln х – dх = х ln х – х + С..
Теорема Ньютона–Лейбница.
Пусть функция f непрерывна на [а,в]. тогда она интегрируема на любом отрезке, [а,х], где а £ х £ в, то есть, для любого х Î [а,в], существует интеграл
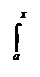F(х) = f(t)dt (V)
Если f(t)³0 " tÎ[а,в], то F(х) = S(х), где S(х) – площадь криволинейной трапеции аАL(х) (рис. 5)
 |
Определение. Функция F определённая соотношением (V) на [а,в] называется интегралом с переменным верхним пределом.
Эта функция непрерывна и дифференцируема на [а,в]. А именно имеет место следующая теорема.
Теорема. (Ньютона–Лейбница)
|
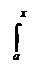
F’(х) = ( f(t)dt) = f(х)1, х Î [а,в] .
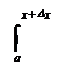
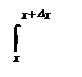Доказательство: Пусть х Î [а,в], х + Dх Î [а,в]; тогда в силу теоремы 1 пункта 2.12. получим
F(х + D х) = f(t)dt = f(t)dt + f(t)dt
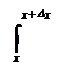Найдём соответствующее приращение DF функции F. Используя равенства (V) и теорему 4 пункта 2.12. имеем
DF = F(х + D х) – F(х) = f(t)dt = f(с) D х, где
с Î [х, х + D х]
|
|
|
|
|
Если Dх ® 0, то х + Dх ® 0 и с ® х, так как с Î [х, х+ D х]. Тогда в силу непрерывности f получим
|
Что и требовалось установить.
Легко вытекает следующее утверждение: всякая непрерывная на [а,в] функция имеет на этом отрезке первообразную при этом одной из первообразных является интеграл (V).
|
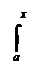Действительно, пусть функция f непрерывна на [а,в]; тогда она интегрируема на любом на [а,х], где х Î [а,в], то есть, существует интеграл (V), который и является первообразной функцией для f . Следовательно, неопределённый интеграл от непрерывной на [а,в] функции f можно записать в виде
f(х)dх = f(t)dt + С, х Î [а,в]
где С – произвольная постоянная.
Формула Ньютона–Лейбница.
Теорема. Если Ф – первообразная для непрерывной на [а,в] функции f, то определённый интеграл от функции f вычисляется по формуле
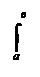f(х)dх = Ф(в) – Ф(а).
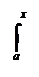Доказательство: Пусть Ф некоторая первообразная для функции f . В силу предыдущей теоремы функция (V) также является первообразной для функции f . Поскольку две первообразные Ф и F отличаются друг от друга на некоторую постоянную, имеем
f(х)dх = Ф(х) + С (1)
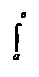Положим в последнем равенстве х = а. Так как
f(х)dх = 0,
то Ф(а) + С = 0, откуда С = – Ф(а)
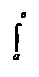Подставляя найденное значение С в соотношение (1), имеем
f(х)dх = Ф(х) – Ф(а).
Полагая в последнем соотношении х = в и обозначая переменную t через х, окончательно получим равенство указанное в теореме.
|
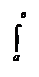Формулу Ньютона–Лейбница в сокращённом виде принято записывать так:
f(х)dх = Ф(х)| = Ф(в) – Ф(а)
|
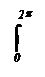Примеры.
1)
|
|
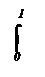sin хdх = – cos х| = – cos 2 p + cos 0 = 0.
2) 
= ln |x + x2+1| = ln (1+Ö2) – ln 1 = ln (1+Ö2)
Интегрирование по частям.
Пусть функции f(х) и j(х) непрерывны вместе со своими производными в интервале [а,в]. Пусть, далее,
F(х) = f(х) j(х).
Тогда F’(х) = f(х) j’(х) f’(х) j(х).
|
|
|
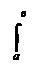
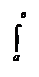то [f(х) j’(х) f’(х) j(х)]dх = f(х) j(х)| ,
откуда f(х) j’(х)dх = f(х) j(х)| – f’(х) j(х)dх
Примеры.
1) 
Вычислить интеграл.
х cos х dх
|
х cos х dх = х sin х| – sin х dх = –2
2) 
Вычислить интеграл
ln х dх.
|
|
|
= [х ln х] – [х] = 2 ln2 – 1 = ln4 – 1
Теорема Паскаля.
Среди последователей Кавальери самыми видными учёными, подготавливавшими создание интегрального и дифференциального исчисления, были Дж.Валлик, П.Ферма, Б.Паскаль.
|
Вычислением интегралов от степеней хr, или, как говорили в то время, квадратурой «парабол» у = хr, где r – рациональное число, П.Ферма занимался ещё в 1644 г. позже Ферма изложил общую теорию всех различных случаев.
Ещё более чётко понятие определённого интеграла выступает в трудах Б.Паскаля. все его усилия были направлены на уточнение метода неделимых. Попытка уточнения состоит в том, что он сумму всех неделимых понимал как сумму элементарных площадок, образуемых бесконечно близкими, одинаково отстоящими друг от друга ординатами, ограниченными отрезком оси абсцисс и кривой (то есть сумму вида åуdх). В ряде задач он вводил сумму всех синусов, определяя её как сумму произведений ординат на элементы дуги (åуds), которая в случае окружности единичного радиуса оправдывает своё название (åsin jd j).
Для примера рассмотрим следующую теорему из «Трактата о синусе четверти круга» (1658) Паскаля:
 |
Сумма синусов какой–нибудь дуги (BF) четверти круга (рис. 9) равна отрезку основания (АО) между крайними синусами, умноженному на радиус (АВ).
Дуга BF делится на равные части, отмеченные точками из которых из которых проводятся синусы DI. Точки пересечения касательных к дуге окружности в точках D обозначены точками Е; из последних затем опускаются перпендикуляры ER.
Предварительно Паскаль указывает, что
DI . EE = RR . AB (1)
Действительно (рис. 10), из подобных прямоугольников DIA и EKE (ÐЕЕК = ÐDAI) следует:
AD/DI = EE/EK
Ввиду того, что AB = AD, получаем равенство (1).
«Я утверждаю, — пишет после этого Паскаль, — что сумма синусов DI каждого умноженного на одну из равных дуг DD, равна прямой АО умноженной на радиус АВ». Заменяя каждую касательную ЕЕ дугой DD, Паскаль получает в левой части равенства (1) «сумму синусов», а в правой произведение АВ на сумму отрезков RR, то есть, на АО. Итак, теорема доказана. Отождествление дуги DD с отрезком касательной Паскаль только подразумевает.
Чтобы перевести доказательство Паскаля на современный язык введём соответствующую систему декартовых координат, обозначим «синус DI» через у, элемент дуги DD – через ds, дифференциал независимого переменного – через dх, радиус АВ – через r. Тогда равенство (1) можно записать так:
уds = rdх
Интегрируя согласно содержанию теоремы Паскаля, получим:
уds = rdх. (2)
Более сложный интеграл, стоящий в левой части этого равенства, сводится таким образом к более простому интегралу правой части, равному rx, а для целой четверти r2.
Положим r = 1 и введём угол DAB = Ð ADI = j. Тогда (рис. 10)
S = rj = j, у = DI = AD cos j = cos j, х = sin j.
Равенство (2) даёт:
cos j dj = х = sin j.
На рассмотренном выше DЕЕК Лейбниц построил своё дифференциальное исчисление и назвал его характеристическим.
Метод флюксий» Ньютона.
Независимо от Лейбница и ещё до него эти результаты были получены Ньютоном. Последний, однако, нашёл их, идя по другому пути. Ньютону принадлежат в областях науки первоклассные достижения, в том числе и разработка дифференциального и интегрального исчисления в форме метода флюксий.
В своём «Методе флюксий» автор формулирует две основные проблемы. Первая:
«По данному соотношению между флюэктами определить соотношение между флюксиями».
Решение этой проблемы приводит Ньютона к вычислению флюксии (производной) от данной флюэнты (функции) и к своеобразному обоснованию развитого или дифференциального исчисления. Он вводит понятие «моментов» текущих величин, соответствующих понятию дифференциалов функций. Неограниченно малую величину, понимаемую актуально бесконечно малое приращение независимой переменной (времени), Ньютон обозначает через знак O, напоминающий нуль, но не являющийся нулём. Момент флюэнты и, например он обозначает так ио, где и – флюксия. По существу момент флюэнты это её дифференциал.
Вторую проблему Ньютон формулирует так.
«По данному уравнению содержащему флюксии, найти соотношение между флюэктами». Это общая проблема объём интегрировании обыкновенных дифференциальных уравнений, которую Ньютон решает главным образом с помощью бесконечных рядов, содержит в частности задачу определения функции F (называемую первообразной), зная её производную F’ = f. Именно эта задача приводит к понятию неопределённого интеграла.
Многие задачи из механики и физики ведут к понятию первообразной функции неопределённого интеграла, однако исторически, в частности у Ньютона, это понятие возникло из геометрии как задача квадратуры кривой.
Пусть имеем криволинейную трапецию (рис. 11), ограниченную сверху кривой у = f(х), и пусть эта функция непрерывна на [а,в] и принимает лишь неотрицательное значение.
Для нахождения площади Р нашей трапеции рассмотрим сначала площадь Р(х) фигуры АDLK, отвечающей промежутку [а, х], где х – произвольно взятое на [а,в] значение. Для нахождения функции Р(х) построим приращение Dх и соответствующее ему приращение DР, если т и М предоставляют минимум, соответственно, максимум f(х) в промежутке [х, х+Dх], то, очевидно, будет иметь место неравенство
т Dх < DР < МDР ,
откуда т < DР/Dх < М.
Вследствие непрерывности функции м и М будут стремиться к f(х) при стремлении Dх к нулю, и мы получим:
|
то есть, производная от переменной Р(х) по конечной абсциссе х равна конечной ординате у = f(х), или, тоже, площадь Р(х) криволинейной трапеции есть первообразная функция для функции у = f(х), представляющей собой кривую ограничивающую трапецию.
Можно теперь записать:
Р(х) = F(х) +С. (V)
Но так как при х = аР(х) = 0, получим для значения постоянной С в нашем случае:
0 = F(а) + С, или С = – F(а),
подставив это значение С в (V), будем иметь:
Р(х) = F(х) – F(а), (W)
Для определения площади Р всей криволинейной трапеции ABCD следует положить х = в.
Тогда
Р = F(в) – F(а).
Таким путём исходя из понятия производной, Ньютон пришёл к понятию первообразной или неопределённого интеграла. Последний являлся для Ньютона первоначальным понятием при построении интегрального исчисления.
Равенство (W), пользуясь современными символами, можно переписать так:
f(х)dх = F(х) – F(а).
Это и есть так называемая формула Ньютона–Лейбница. В ней определённый интеграл, рассматриваемый как функция верхнего переменного предела интегрирования представлен в виде одной из первообразных F(х) + С подынтегральной функции f(х).
Итак, задача вычисления площади фигур, то есть, квадратура, ведёт к понятиям как определённого, так и неопределённого интегралов.
Поэтому вычисление интегралов стали называть квадратурой.
Дифференциальные методы.
В математике XVII в. наряду с интегральными методами складывались и методы дифференциальные. К дифференциальным методам мы отнесём те, в которых содержатся элементы будущего дифференциального исчисления. Вырабатывались эти элементы при решении задач, которые в настоящее время решаются с помощью дифференцирования. Такие задачи были в то время трёх видов: определение касательных к кривым, нахождение максимумов и минимумов функций и отыскивание условий существования алгебраических уравнений кратных корней.
Накопление элементов дифференциального исчисления наиболее явную форму приняло у Ферма. В 1638 г. он сообщил в письме Декарту, что решил задачу определения экстремальных значений f(х) .
 |
Ферма составил уравнение [f(х + h) – f(х)] / h = 0 и после преобразований в левой части полагал h = 0. Вопреки мнению позднейших исследователей, которые видели в этом идеи исчисления бесконечно малых, в действительности Ферма нашёл это условие и аналогичное
[f(у) – f(х)] / [у–х] = 0
Так же близок к дифференциальному исчислению метод Ферма отыскания касательных к алгебраическим кривым.
На малой дуге MN алгебраической кривой f(х) = 0 путём проведения секущей SMN строится «характеристический» D MNP.
D MNP подобен D MRS.
Отсюда SR = (MR . MP) / PN, или в более привычных нам символах SP = [f(х)h] / f(х+h) – f(х).
Затем Ферма переходит от секущей к касательной, полагая х = 0, получая тем самым St = у / у1. Позднее он распространил этот метод определения касательных на случай неявной функции f(х,у) = 0. Полученное им выражение легко переводится в привычное нам
дf / дх + у1 (дf / дх) = 0.
Первый в мире печатный курс дифференциального исчисления опубликовал в 1696 г. Лопиталь. Этот курс состоит из предисловия и 10 глав. В предисловии даётся краткий исторический обзор развития нового исчисления.
В 10 главах книги излагаются определения постоянных и переменных величин и дифференциала («Бесконечно малая, часть на которую непрерывно увеличивается или уменьшается переменная величина, называется её дифференциалом».), объясняются употребляющиеся обозначения dх, dу и др., выводятся правила дифференцирования алгебраических выражений, определяется дифференциальное исчисление к нахождению касательных к кривым, к нахождению максимумов и минимумов и т.п.
Большими достоинствами книги Лопиталя являются простота и строгая последовательность изложения, обилие примеров лёгких, средних и более трудных.
Появление анализа бесконечно малых революционировало всю математику, превратив её в математику переменных величин.
Литература.
1. Стефан Бонах
«Дифференциальные и интегральные исчисления».
2. Глаголев А.А., Солнцева Т.В. «Курс высшей математики».
3. Глейзер Г.И. «История математики в школе».
4. Рыбников К.А. «История математики».
5. Стройк Д.Я. «Краткий очерк истории математики».
6. Шестаков А.А. Малышева И.А. «Курс высшей математики».
7. Хрестоматия по истории математики.
Астраханский Государственный Педагогический Университет
Бакалаврская работа
Студентки IV курса физико–математического факультета
Ночевной Светланы Павловны
Кафедра:
Математического анализа
Тема:
Основные понятия дифференциального исчисления и история их развития
Научный руководитель
ст. преподаватель
Пономарёва Н.Г.
Астрахань
Г.
План.
1. Основные понятия дифференциального исчисления функций одной переменной.
1.1. Определение производной и её геометрический смысл.
1.2. Дифференциальные функции. Определение дифференциала.
1.3. Инвариантность формы первого дифференциала.
1.4. Дифференциал суммы, произведения и частного.
1.5. Геометрическая интерпретация дифференциала.
2. Основные понятия интегрального исчисления функций одной переменной.
2.1. Первообразная функция и неопределённый интеграл.
2.2. Геометрический смысл неопределённого интеграла.
2.3. Основные свойства неопределённого интеграла.
2.4. Метод непосредственного интегрирования.
2.5. Метод замены переменной (способ подстановки).
2.6. Интегрирование по частям.
2.7. Определённый интеграл как предел интегральной суммы.
2.8. Основные свойства определённого интеграла.
2.9. Геометрический смысл определённого интеграла.
2.10. Теорема Ньютона–Лейбница.
2.11. Формула Ньютона–Лейбница.
2.12. Замены переменных в определённых интегралах.
2.13. Интегрирование по частям.
3. Исторические сведения о возникновении и развитии основных понятий.
3.1. Происхождение понятия определённого интеграла и инфинитезимальные методы Архимеда.
3.2. От Архимеда к Кеплеру и Кавальери.
3.3. Теорема Паскаля.
3.4. «О глубокой геометрии» Лейбница.
3.5. «Метод флюксий» Ньютона.
3.6. Дифференциальные методы.
Цель работы: «Изучить основные понятия дифференциального и интегрального исчислений и ознакомиться с историей их развития».
Основные понятия дифференциального исчисления функций одной переменной.
Определение производной и её геометрический смысл.
Пусть функция y = f(х) определена в окрестности точки хо. возьмём точку х1 этой окрестности, отличную от хо.
Определение. Разность х1 – х0, которую обозначают символом Dх, будем называть приращением независимой переменной.
Определение. Подобным образом соответствующая разность
у1 – у0 = f(х1) – f(х0), обозначается символом Dу и называется приращением зависимой переменной, или приращением функции.
Получаются следующие соотношения:
х1 = х0 + Dх,
у1 = у0 + Dу,
у0 + Dу = f(х0 + Dх)
Так как у0 = f(х0),
то Dу = f(х0 + Dх) – f(х0).
|
Определение. Частное будем называть разностным отношением.
Выражение f(х0+ Dх)– f(х0)
Dх
(принимая что х0 имеет определённое постоянное значение) можно считать функцией приращения Dх.
Определение. Если предел этого выражения при Dх, стремящемся к нулю, существует, то его мы будем называть производной функции у = f(х) по х в точке х0
|
|
Пример. у=х2 . Вычислите производную для х=2.
Имеем: f(х+Dх) = (х+Dх)2 ,
Поэтому Dу = (х+Dх)2 – х2 = 2хDх+(Dх)2
|
Отсюда = 2х+Dх
| |||
| |||
Переходя к пределу получим: = 2х + = 2х.
|
|
была непрерывной в точке х0.
Рассмотрим график функции у = f(х) (рис.1)
|
Легко заметить, что отношение равно тангенсу угла a, образованного положительным направлением секущей, проходящей через точки А и В (соответствующие точкам х и х+Dх), с положительным направлением оси Ох, то есть, от А к В если теперь приращение Dх будет стремиться к нулю, точка В будет стремиться к А, то угол a будет стремиться к s, образованному положительным направлением касательной с положительным направлением оси Ох, а tg a будет стремиться к tg s.
|
Таким образом, можно утверждать следующее:
Производная в данной точке х равна тангенсу угла, образованного положительным направлением касательной в соответствующей точке (х,f(х)) нашей кривой с положительным направлением оси Ох.
Дата: 2019-12-22, просмотров: 271.
