Теорема Котельникова:

Сигнал с ограниченным спектром можно представить в виде последовательности выборок взятых с частотой f_{дискритизации} ³ 2*f_max

Если условие не соблюдается, произойдет искажение в следствии наложения. (см рисунок спектр сигнала)

 .

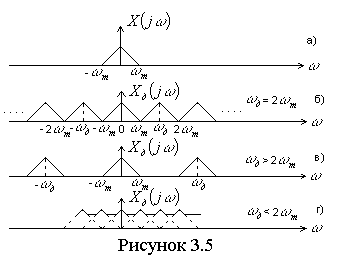
На рисунке показаны: спектр непрерывного сигнала, ограниченный частотой w_m (рисунок а) и спектры дискретизированного сигнала, соответствующие различным частотам дискретизации (рисунки б-г).

Проанализируем результаты, представленные на рисунке 3.5. Как видно из графиков при выполнении условия

слагаемые спектры дискретизированного сигнала либо не соприкасаются (рисунок 3.5в), либо примыкают друг к другу (рисунок 3.5б), но не перекрываются. Перекрытие слагаемых спектров происходит лишь в том случае, когда условие (3.17) не выполняется и w_¶<2× w_m. Очевидно, что при выполнении (3.17), используя идеальный фильтр низких частот с частотной характеристикой вида 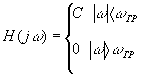(3.18), где C=const>0, и полагая w_гр=w_m можно по дискретизированному сигналу точно восстановить спектр X(jw) функции x(t), а, следовательно, и саму эту функцию, отфильтровав все боковые спектры 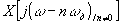. Математически это преобразование описывается следующим образом:
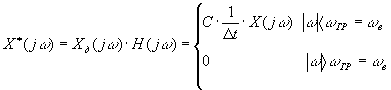(3.19), где X^*(jw) - спектр сигнала на выходе восстанавливающего фильтра. Равенство 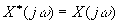, получающееся при 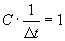, означает, что 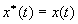, где 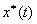- сигнал на выходе фильтра, так как одна и та же спектральная плотность не может соответствовать двум различным временным функциям. Графическая иллюстрация восстановления показана на рисунке 3.6.
Из условия 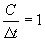уточним коэффициент передачи фильтра: так как 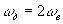, т.е. 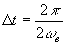, то 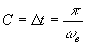(3.20). 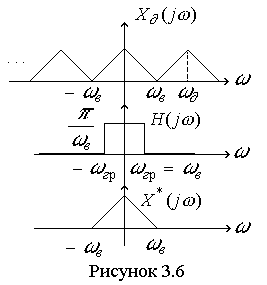Если неравенство (3.17) не выполняется, то из-за взаимного перекрытия слагаемых Х[j(w-nw₀)] происходит изменение формы спектра Х_¶(jw) (см. 3.5 г) и точное восстановление Х(jw), а следовательно и x(t) невозможно. Таким образом, при выполнении неравенства (3.17) процесс с дискретным временем x_¶(t), являющийся результатом дискретизации непрерывного процесса х(t), теоретически содержит всю информацию о всех значениях непрерывного процесса х(t).
Данное утверждение и составляет основное содержание теоремы Котельникова. Проведенные рассуждения составляют один из возможных вариантов доказательства этой теоремы

Теорема Котельникова во временной области.

Переход решетчатой функции от непрерывной возможен только с ограничениями. Причина ограничений состоит в том, что нужно сохранить возможность восстановления исходной функции f(t), здесь необходимо учитывать ряд факторов:

1) характер изменения сигнала;

2) скорость изменения регистрации сигнал и т.д.

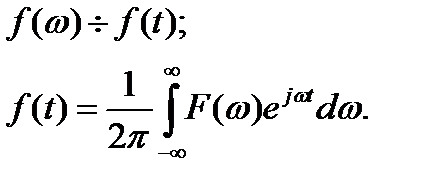
Наложим частотное ограничение. 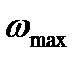-наивысшая частота сигнала f(t).

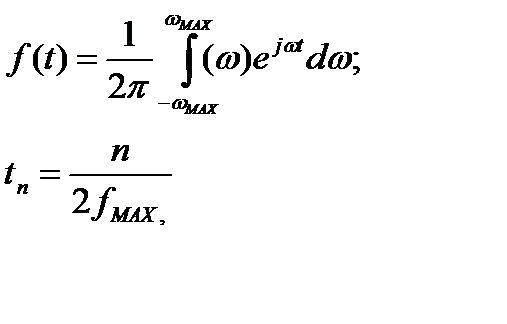
где n-текущее значение отсчётов, 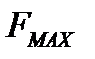- максимальная частота.

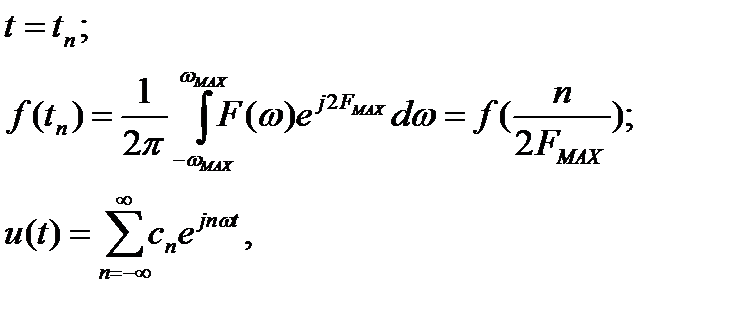
где 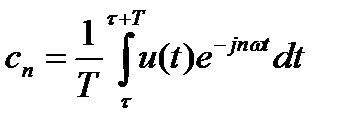коэффициент разложения в ряд Фурье.

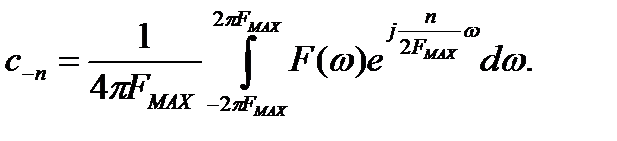
Сравним 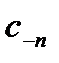 и :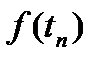

.

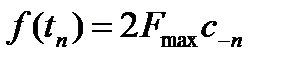Отсюда видно что функция f(t) полностью определяется своим спектром F(w) может быть представлено своим разложением в ряд Фурье, то отсюда следует, что f(t) определяется через свои значения взятые в точках 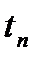 с частотой 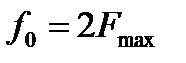. Из сказанного выводится теорема Котельникова:

Если функция f(t) не содержит частот больших 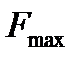, то она полностью определяется дискретным множеством своих значениях взятых с частотой  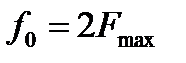, где 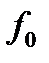-частота дискретизации.

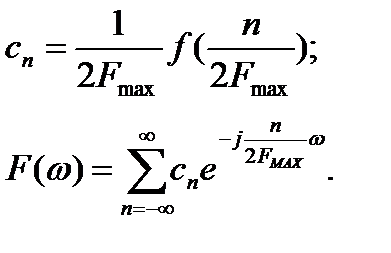
Используем обратное преобразование Фурье:

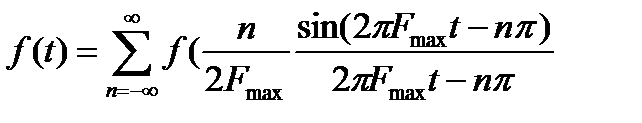-выражение в аналитической форме f(t), то есть ряд Котельникова.

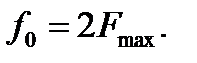
На практике: .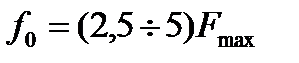

Такой выбор является следствием компромисса между стремлением поднять частоту дискретизации и целью получить сигнал, который может быть более точно воспроизведён в исходном виде и условиями экономии ширины полосы при передаче информации.

Теорема Котельникова в частотной области.

 f(t) ;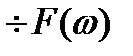

F(w)= ,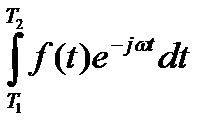

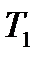 и 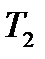-пределы вне которых функция f(t) равна нулю.

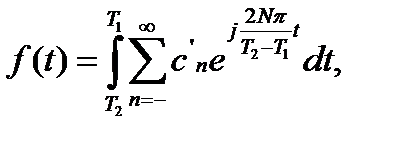 где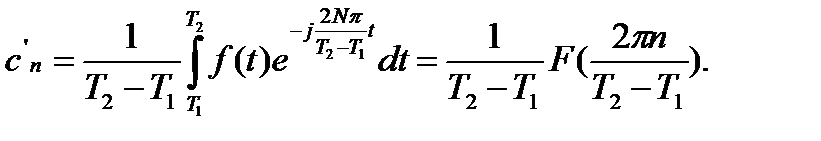

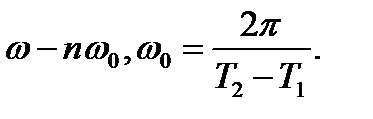
Отсюда мы можем вывести теорему Котельникова:

Если f(t) определена только на интервале 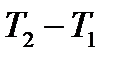, то её спектр F(w) полностью определяется дискретным множеством своих значений, взятых в равноотстоящих точках, разделённых интервалом .

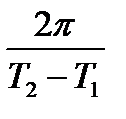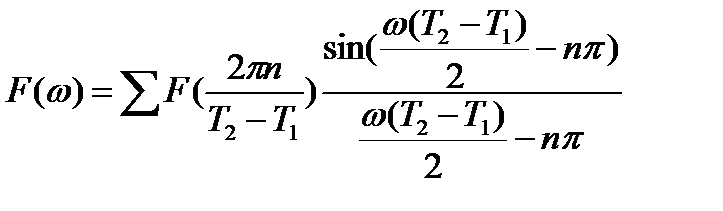-ряд Котельникова в частотной области.

Энергия дискретизированной функции.

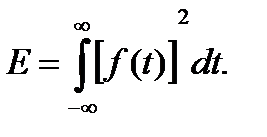
Теорема Парсеваля, позволяет утверждать, что среднеквадратичное значение f(t) равно сумме квадратов абсолютных значений коэффициента разложения этой функции в ряд Фурье.

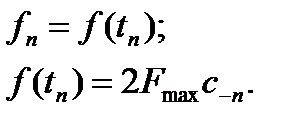
Заменим f(t) на решетчатую функцию :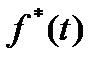

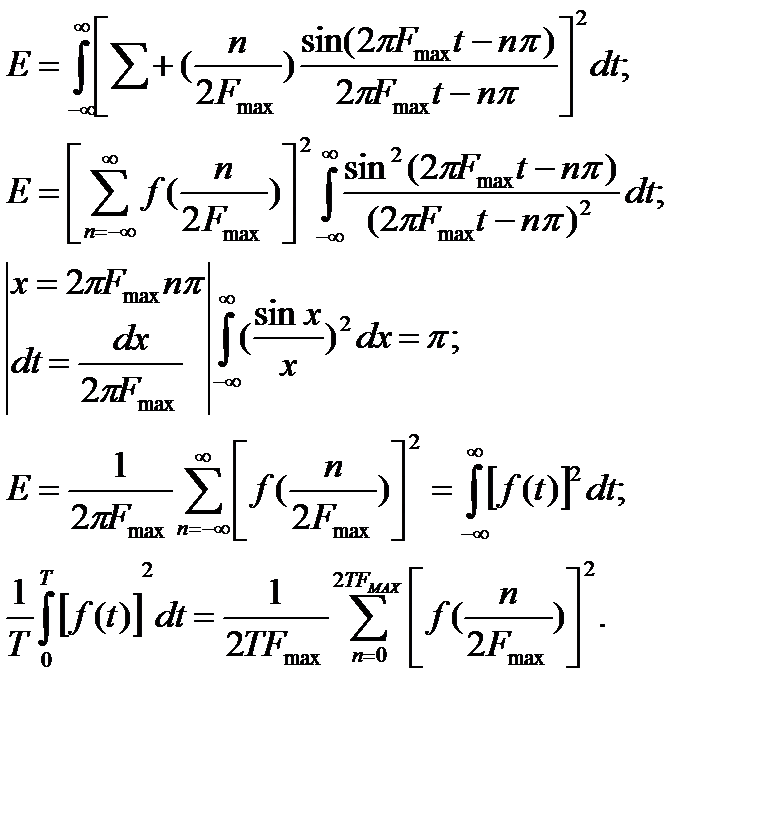
Квантование

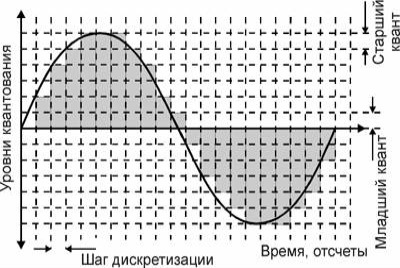
Квантование – процесс перехода от бесконечного множества амплитуд к конечному.

Т.е. амплитуду определяем до ближайшего уровня. Это дает возможность закодировать сигнал (каждому уровню присваивается свой код).

Ошибка (расстояние до ближайшего уровня) при округлении – ошибка квантования (искажение квантования или шум квантования)

Зависит от количества уровней (т.е. от шага квантования)

После квантования сигнал может принимать ограниченное число состояний или отчётливых различных сигналов.

Характеристика квантования:

y

                               X

Если ступенчатая функция характеризуется одинаковой величиной ступенек, то такая характеристика называется регулярной. Если ступени неодинаковые, то нерегулярной. Характеристика квантователя меняется во времени. При квантование имеется опасность появления флуктуации – выходного сигнала при переходе от одной ступени к другой, из за нечастого квантования (шум-квантования).

Квантование является нелинейной операцией. Точность зависит от того, насколько мала ступень квантования.

Ошибка квантования e(t)- функция элементарного уровня, она не может превышать значение q, её можно рассмотреть как шум; 0 .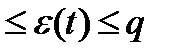

Частота квантования связана с x(t), которая в свою очередь связана с частотой сигнала в этом спектре.

e(t) может рассматривать как последовательность отрезков, с переменной амплитудой ±q+2.

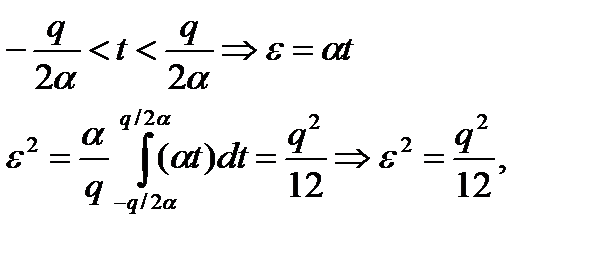
где a-переменная крутизна.

Чем меньше ступень квантования, тем меньше шум.