ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»

Орловский филиал

Кафедра «Математика, информатика и общегуманитарные дисциплины»

Е.С. Филонова

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ФИНАНСОВЫХ РАСЧЕТОВ

Методические рекомендации по изучению дисциплины

И выполнению контрольной работы

Для студентов,

обучающихся по направлениям подготовки

38.04.01 Экономика, 38.04.02 Менеджмент

(заочная форма обучения)

ОРЕЛ 2018

Методические указания обсуждены

на заседании кафедры «Математика, информатика и общегуманитарные дисциплины»

(Протокол № 01 от 14 сентября 2018 г.)

Зав. кафедрой – кандидат физико-математических наук, доцент

Е.С. Филонова

Введение

Дисциплина части образовательной программы, формируемой участниками образовательных отношений; модуль инвариантных дисциплин.

Цели дисциплины:

- развитие теоретико-практической базы и формирование уровня математической подготовки, необходимых для понимания основных идей применения математических методов финансовых расчетов в экономике, финансах и бизнесе;

- развитие математической базы и формирование уровня практической подготовки, необходимых для применения математических методов финансовых расчетов в финансовой деятельности и для решения задач финансового планирования.

Задача дисциплины:

- в результате изучения дисциплины «Математические методы финансовых расчетов» студенты должны владеть основными математическими понятиями дисциплины; уметь использовать методы финансовых вычислений для решения теоретических и прикладных задач экономики и финансов, уметь решать исследовательские задачи, иметь навыки работы со специальной математической литературой.

В процессе изучения дисциплины «Математические методы финансовых расчетов» студенты самостоятельно выполняют домашнюю контрольную работу.

Цели контрольной работы – усвоить теоретические основы дисциплины, выработать навыки в решении задач, соответствующих тематическому плану дисциплины, и овладеть математическими методами финансовых вычислений для решения прикладных и исследовательских задач экономики и финансов.

1. Методические указания по выполнению и оформлению контрольной работы

Контрольная работа по дисциплине «Математические методы финансовых расчетов» состоит из пяти заданий по различным темам курса.

В каждой задаче контрольной работы необходимо привести подробное решение и сделать обоснованные экономические выводы. Численное решение задач следует подкреплять использованием компьютерных технологий.

Решение заданий должно сопровождаться необходимыми комментариями, то есть все основные этапы решения задачи должны быть раскрыты и обоснованы соответствующими теоретическими положениями.

Варианты заданий определяются по последней цифре номера личного дела (зачетной книжки) студента.

Контрольная работа выполняется и защищается в сроки, установленные учебным графиком.

Титульный лист контрольной работы должен содержать все необходимые реквизиты:

- названия университета и филиала;

- название кафедры;

- направление подготовки;

- наименование учебной дисциплины;

- Ф.И.О. студента и номер его зачетной книжки;

- Ф.И.О. преподавателя;

- дату сдачи работы на проверку.

К собеседованию допускаются студенты, выполнившие правильно и в достаточном объеме все задания контрольной работы. Для получения зачета по результатам собеседования студент должен выполнить работу над ошибками в проверенной преподавателем контрольной работе, проработать теоретические основы методов решения задач и ответить на вопросы преподавателя.

Критерии и баллы текущего контроля по дисциплине

№ п.п.	Вид работы	Максимальное количество баллов
1	Посещаемость аудиторных занятий и активность работы на них	6
2	Выполнение задания № 1 контрольной работы	15
3	Выполнение заданий № 2-5 контрольной работы, в т.ч.	14
	Задание № 2	3
	Задание № 3	2
	Задание № 4	6
	Задание № 5	3
4	Подготовка и презентация творческого проекта	5

ИТОГО за семестр

2. Основные формулы и примеры решения задач по теме «Теория процента. Простой процент»

2.1. Основные формулы финансовых операций с простыми процентами при постоянных: процентной ставке и временном интервале

Простой процент - это начисление процентов по периодам на первоначально инвестированную сумму.

В общем случае финансовой операции наращения по схеме простого процента формула имеет вид

FV = PV (1 + r ∙ t), (2.1)

где t – срок инвестирования в годах;

r – годовая процентная ставка в долях единицы;

PV – начальная сумма инвестирования;

FV – наращенная сумма по истечении t лет.

Множитель (1 + r ∙ t ) в формуле (2.1) называется множителем наращения или коэффициентом наращения простых процентов.

На практике многие финансовые операции выполняются в рамках одного года и тогда формула для начисления простого процента в течение периода времени, которое меньше года будет иметь вид

FV = PV ( 1 + r · ¾) , (2.2)

где FV - сумма, получаемая при начислении процента за t дней;

PV – первоначально инвестированная сумма;

t – количество дней начисления процента в течение года;

r - годовая процентная ставка в долях единицы;

T – длительность года в днях.

Заметим, что простые проценты

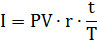
пропорциональны сроку вклада и процентной ставке.

Формула (2.2 ) носит общий характер, поскольку под t можно понимать любой интервал времени: день, месяц, квартал, год и т.д.. При этом показатель Т должен принимать соответствующие значения: 365 или 360, 12, 4, 1 и т.д.

Определяя продолжительность ссудо-заемной операции, принято день выдачи ссуды и погашения ее считать одним днем. При подсчете числа дней t срока ссудо-заемной операции в настоящее время применяются три схемы:

а) Способ «365/365». Точный процент и точная продолжительность периода (число дней в году 365 или 366 и t точное). Это наиболее точная схема и применяется в банках Великобритании и США.

б) Способ «365/360». Обыкновенный процент и точная продолжительность периода (число дней в году, квартале и месяце определяется приближенно, соответственно: 360, 90, 30 и t -точное). Эта схема дает несколько больший результат и применяется в банках Франции и Бельгии.

в) Способ «360/360». Обыкновенный процент и приблизительная продолжительность периода (число дней в году, квартале и месяце определяется приближенно, соответственно: 360, 90, 30 и t – приблизительное, т.к. считается, что в месяце 30 дней). Это менее точная схема и применяет в банках Германии, Дании и Швеции.

В предлагаемых схемах при расчете точного числа дней t пользуются специальными таблицами (одна для обычного года, а другая для високосного), в которых все дни года последовательно пронумерованы. Продолжительность финансовой операции определяется вычитанием номера первого дня из номера последнего дня.

В российской практике ссудо-заемных операций используются все три схемы.

Пример.

Инвестор размещает на счете в банке сумму 1000000 руб. под 20% годовых. Определить какую сумму получит вкладчик через 300 дней, используя в расчетах способ «360/360».

Решение.

Согласно (2.1) имеем

FV = 1000000 ( 1 + 0.2· 300/360 ) = 1666666,67 руб.

Пример.

Вкладчик размещает на счете в банке 75000 руб. Банк начисляет простые проценты раз в квартал по ставке 20% годовых. Найти процентный платеж и сумму, какую он получит через полтора года.

Решение.

Наращенную сумму рассчитаем по (2.2), а проценты по выражению для I представленному выше:

I = 75000 ·0.2∙ 6 / 4 = 22500 руб.;

FV = 75000 (1+0.2∙ 6 / 4) = 97500 руб.

! Пример. Начисление простых процентов

Вкладчик хочет разместить на счете в банке 75000 руб. Банк А начисляет простые проценты раз в месяц по ставке 20% годовых, а банк Б раз в полгода но по ставке 25% годовых. Определить, в каком из банков вкладчику необходимо разместить вклад, чтобы получить наибольший доход, если он намерен держать деньги в банке 2 года.

Решение.

Для анализа используем расчетную схему (2.2) для простых процентов:

FV_А = 75000 (1+0.2∙ 24 / 12) = 105000 руб.;

FV_Б = 75000 (1+0.25∙ 4 / 2) = 112500 руб.

Вкладчику необходимо разместить вклад в банке Б.

! Пример. Три варианта начисления простых процентов

Предоставлен кредит в размере 5 млн. руб. 25 января с погашением через 6 месяцев (25 июля) под 40% годовых. Рассчитать различными способами сумму к погашению, если год не високосный.

Решение.

Возможные варианты возврата кредита:

А) Точный процент и точное число дней.

Точное число дней определяется по таблицам с номерами дней года ( t = 206 – 25 = 181 дн.)

FV₁₈₁ = 5·( 1 + 0,4 · 181/365 ) = 5,9918 млн. руб.

Б) Обыкновенный процент и точное число дней.

FV₁₈₁ = 5·( 1 + 0,4· 181/360 ) = 6,0056 млн. руб.

В) Обыкновенный процент и приближенное число дней.

Приближенное число дней кредита равно: 5 дн. января (30 - 25) + 150 ( 30 дн. в 5 месяцах: февраль, март, апрель, май, июнь) + 25 дн. июля = 180 дн.

FV₁₈₀ = 5 ·(1 + 0,4·180/360) = 6,0000 млн. руб.

2.2 Основные формулы финансовых операций с простыми процентами при переменных: процентной ставке и временном интервале

В практике финансовых расчетов, особенно при учете темпа инфляции, приходится часто изменять ставку простых процентов. Пусть в начальный момент времени инвестор вложил в некоторый банк сумму PV. За время инвестиционного периода t изменение годовой процентной ставки происходило m раз на следующих временных интервалах имеющих размерность в долях года:

t₁, t₂,t₃, … , t_m,

причем на каждом интервале годовая процентная ставка оставалась постоянной и была равна соответственно:

r₁, r₂, r₃, … , r_m

В этом случае наращенная сумма к концу инвестиционного периода будет

FV = PV+PV r₁ t₁+PV r₂ t₂ + … + PV r_m t_m = 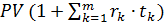(2.3)

Пример.

Вкладчик разместил вначале года 100000 руб. в банке. Договор предусматривает следующую схему начисления простых процентов: 1 год – 20%, в каждом последующем полугодии ставка повышается на 10%. Найти величину вклада через 2 года, если проценты начисляются по схеме простых процентов.

Решение.

Применяя формулу (2.3), сумма вклада будет

FV₂ = 100 000 (1 + 0,2·1+0,3· 0,5 + 0,4· 0,5) = 155 000 руб.

! Пример. Плавающая процентная ставка

Вкладчик разместил вначале года 50000 руб. в банке. Ставка рефинансирования[1] ЦБ на момент заключения договора равна 30% годовых. Договор предусматривает следующую схему начисления простых процентов: 1 квартал – 50% от ставки рефинансирования ЦБ, в каждом последующем квартале ставка понижается на 10% от ставки рефинансирования ЦБ. Найти величину вклада через 1 год, если проценты начисляются по схеме простых процентов.

Решение.

Определяя квартальные процентные ставки и применяя (2.3), рассчитаем величину вклада через год

FV₁ = 50000 + 50000·0,15·0,25 + 50000· 0,12· 0,25 + 50000·0,09·0,25 +50000· 0,06· 0,25 = 50000·(1 + 0,0375 + 0,03 + 0,0225 + 0,015) = 55250 руб.

2.3 Процентный ключ (дивизор)

Процентный платеж в формуле (2.2) можно записать в виде

PV∙ t PV∙ t

I = = . (2.4)

Т / r D

Здесь D = Т/r называется процентным ключом, постоянным делителем или дивизором, а PV∙ t называется процентным числом.

Дивизор численно равен такому количеству денежных единиц, с которого при процентной ставке r получается 1 дн. ед. дохода в день.

Если процентная ставка r^' выражается в процентах, то формула для расчета дивизора будет

D = 100 ∙ Т / r'

Пример.

Найти процентный платеж с капитала 5 000 руб., положенного в банк под 20% годовых на срок 200 дней, если расчет ведется способом «365/365».

Решение.

Воспользуемся выражением для дивизора и формулой (2.4).

D = 100 ∙ 365 / 20 = 1825

I = 5000 ∙ 200 / 1825 = 547,95 руб.

! Пример. Переменная сумма счета и начисление процентов

Сберегательный счет был открыт 3 января, и на него была положена сумма в 10 000 руб. Затем 20 марта со счета были сняты 2 000 руб., 20 апреля добавлена сумма в 1000 руб. и 1 августа счет был закрыт. Все операции осуществлялись в течение года (простой год). Определить сумму полученную владельцем счета, если процентная ставка равнялась 15% годовых, и для начисления процентов применялся способ «365/360». Год обыкновенный.

Решение.

Число дней: для 10000руб. (1 авг. (213) – 3 янв.(3) = 210 дн)

Для 2000 руб.(1 авг. (213) – 20 марта (79) = 134 дн)

Для 1000 руб.(1 авг. (213) - 20 апр. (110) = 103 дн)

Рассчитаем процентные числа

10000 ∙ 210 - 2000 ∙ 134 + 1000 ∙ 103 = 1935000

Дивизор равен

D = 360· 100 / 15 = 2400.

Следовательно, начисленные проценты равны

I = 1935000 / 2400 = 806,25 руб.,

и владелец счета получит

FV = 10000 –2000+1000 + 806,25 = 9806,25 руб.

2.4 Дисконтирование по простым процентам

2.4.1 Математическое дисконтирование

Это процесс обратный наращению капитала. При математическом дисконтировании решается задача нахождения первоначального капитала PV, который через t лет при наращении по схеме простого процента по годовой ставке r приведет к увеличению капитала до значения FV. Из формулы (2.1) следует, что

PV = (2.5)

1 + r· t

В качестве ставки дисконтирования используется процентная ставка r. Разность между FV и PV называется дисконтом D_r.

FV· r · t

D_r = FV - PV = (2.6)

1 + r· t

Дисконт D_r не пропорционален ни времени, ни ставке процента r.

Пример.

Через полгода после заключения финансового соглашения о получении кредита должник обязан заплатить 2,14 млн. руб. Какова первоначальная величина кредита, если он выдан под 14 % годовых и начисляются обыкновенные проценты по схеме "360/360".

Решение.

Расчет ведем по формулам (2.5),(2.6):

PV = FV / (1+ r ∙ t / T ) = 2,14 / ( 1 + 0.14 ∙ 180 / 360 ) = 2 млн. руб.;

D_r = FV - PV = 2,14 - 2 = 0,14 млн. руб.

2.4.2 Банковское дисконтирование (банковский учет)

Существует дисконт, понимаемый как скидка с конечной суммы долга, который может быть установлен сразу в виде некоторой суммы или рассчитан на основе ставки дисконтирования. Этот дисконт называется банковским дисконтом и применяется для учета векселей.

Векселя могут оформляться по разному, однако чаще всего банку приходится иметь дело с суммой к погашению (номинальной стоимостью векселя), т.е. с величиной FV. В этом случае владелец векселя предъявляет его в банк для досрочного погашения. Банк соглашается его купить но, удерживая в свою пользу часть номинальной стоимости векселя, которая обычно называется дисконтом D_d. В этом случае банк предлагает владельцу сумму PV, исчисляемую исходя из объявленной банком ставки дисконтирования (учетной ставки) – d, которая будет меньше номинальной стоимости векселя. Дисконт D_d в этом случае представляет собой проценты начисленные за время t от дня дисконтирования до дня погашения и будет равен

D_d = FV·t ·d (2.7)

И владелец получит

PV = FV (1 - t d) (2.8)

Заметим, что математический дисконт D_r всегда положителен, а из формулы (2.8) следует, что

1 - t d > 0 или t < 1 / d

Если вексель погашается досрочно за t дней до даты законного погашения векселя, то из формулы (2.8) с учетом коэффициента учитывающего относительную длину периода до погашения - t / T , где Т число дней в году, получим следующую формулу для расчета выплачиваемой в этом случае банком суммы

PV = FV ( 1 – d ∙ ¾ ), (2.9)

а для дисконта, имеем

D_d = FV — d (2.10)

! Пример. Банковский учет

Векселедержатель предъявил для учета вексель на сумму 100 000 руб. со сроком погашения 28.09.2017г. Вексель предъявлен 13.09.2017г. Банк согласился учесть вексель с дисконтом в 50 % годовых. Найти сумму, которую получит векселедержатель по векселю.

Решение.

Количество дней от момента учета векселя до погашения:

28.09.2017г.(271). – 13.09.2017г.(256) = 15 дн.

По формуле (2.9) найдем сумму, которую получит векселедержатель

PV = 100000· (1 – 0,5 ∙ 15/360) = 97916,67 руб.

Потребительский кредит

Ломбардный кредит

Задача.

Предпринимателю необходима сумма в 40000 руб. на 3 месяца. Банк предоставил ему кредит в размере 75% от стоимости залога под 12% годовых и за обслуживание долга взыщет 400 руб. Определить величину залога, если кредит выдан 15 мая под простую процентную ставку. Расчетная схема «365/360».

Решение.

1.Номинальная величина кредита PV за вычетом процентного платежа I и платы за обслуживания долга K равна 40 000 руб., следовательно

PV - I - K = 40000 руб. или

PV - I = 40400 руб.

2.Срок кредита

t =15 августа (227) - 15 мая (135) = 92 дня.

3.Найдем процентный платеж:

I = PV· r· t / T,

PV - PV ∙ r ∙ t / T = 40400,

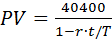
Имеем,

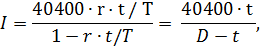
где D = T / r = 360 / 0.12 = 3000.

Тогда

I = 40400 ∙ 92 / ( 3000 - 92 ) = 1278 руб.

Следовательно,

PV = 40400 + I = 40400 + 1278 = 41678 руб.

4. Залог

41678 · 100 / 75 = 55571 руб.

Налоги

Налогообложение играет большую роль в экономике любой страны с рыночной экономикой, т.к. налоги обеспечивают основную часть государственных доходов. Во многих странах облагают и доходы, полученные по срочным банковским вкладам и депозитам (в РФ, если доход превысит ставку рефинансирования ЦБ). Это уменьшает реальную наращенную сумму.

Пусть на сумму PV в течение времени t начисляются проценты по ставке r. Тогда до выплаты налогов процентный платеж равен

I = PV ∙ t ∙ r.

Если ставка налога на проценты равна q, то налоговые платежи с процентов будут

q∙ I = PV ∙ t ∙ r∙ q.

Тогда наращенная сумма с учетом налоговых платежей будет

FV_q = FV- q∙ I = PV∙(1 + t) - PV∙t∙r∙q = PV∙ (1 + t ∙ r∙ (1 – q)) (2.11)

! Пример. Налог и начисление процентов

На депозит была помещена сумма в 30 тыс. руб. под 16% годовых на полтора года, причем начислялись простые проценты. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты равна 12%.

Решение.

Наращенная сумма с учетом налоговых отчислений согласно (2.11) равна

FV = 30 (1 + 1,5 ∙ 0,16 ∙ 0,88) = 36,336 тыс. руб.

Инфляция

Инфляция определяет процесс, характеризующейся повышением общего уровня цен, что практически эквивалентно снижению покупательной способности денег. Инфляция проявляется двояко:

· Переполнение сферы обращения деньгами вследствие их чрезмерного выпуска;

· Сокращение товарной массы в обращении при неизменном количестве выпущенных денег

Основополагающим признаком инфляции является рост цен в среднем, т.е. увеличение усредненной цены корзины товаров и услуг выбранных в качестве базы выявления уровня инфляции. Темпы инфляции определяются с помощью системы индексов цен.

Пусть выбран определенный набор товаров и услуг и пусть за время t его стоимость изменилась с суммы Р₁ до суммы Р_2.

Индексом цен за время t называется величина

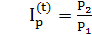(2.12)

Темпом инфляции за время t называется величина

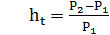(2.13)

Из (2.12) и (2.13) следует соотношение между индексом цен и темпом инфляции за время t

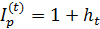(2.14)

Индекс цен за данный период показывает, во сколько раз выросли цены по отношению к уровню цен предыдущего периода. Если известны индексы цен I⁽^t₁⁾_p, I⁽^t₂⁾_p, … , I⁽^t_k⁾_p или темпы инфляции h_t₁, h_t₂, … , h_tk за соответствующие периоды времени t₁, t₂, … , t_k и эти периоды расположены последовательно друг за другом, то индекс цен за время t = t₁ + t₂ + … + t_k будет равен величине

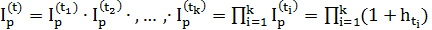(2.15)

В частности, если

h_t1 = h_t2 = … = h_tk = h_,то I^(t)_p = (1+ h)^k

Если за время t была получена некоторая наращенная сумма FV, а индекс цен составил величину I⁽^t⁾_p , то эта сумма с учетом ее обесценения составит:

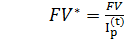(2.16)

Пусть на начальный капитал PV происходит начисление простыми процентами по ставке r в течение времени t и индекс цен за это время равен I⁽^t⁾_p , тогда учитывая обесценение денег за этот период времени, получим

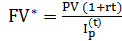(2.17)

Из формулы (2.17) следует, что при

I⁽^t⁾_p= 1+rt

наращение только компенсирует действие инфляции.

Из приведенного выше равенства следует соотношение для минимально допустимой ставки r^{* ,} при которой не происходит уменьшения капитала (эрозии капитала), а именно

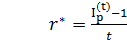
Ставка r которая будет больше r^* называется положительной процентной ставкой, так как в этом случае происходит реальное увеличение капитала.

При инфляции различают: номинальную процентную ставку (r_n), указываемую в финансовых соглашениях и не учитывающую инфляцию, а также реальную процентную ставку (r) скорректированную с учетом инфляции. Реальная процентная ставка всегда меньше номинальной и может быть отрицательной. Положительная реальная ставка - это ставка, при которой происходит реальное увеличение первоначально инвестированного капитала.

Для обеспечения полной компенсации негативного воздействия инфляции, из формулы (2.16) с учетом соответствующих коэффициентов наращения по номинальной и реальной процентным ставкам, получим следующее соотношение

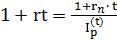. (2.18)

Из формулы (2.18) при известных: реальной процентной ставке, индексе инфляции и времени инвестирования получим выражение для определения номинальной процентной ставки

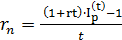(2.19)

а также при известных: номинальной процентной ставке, индексе инфляции и времени инвестирования получим выражение для определения реальной процентной ставки

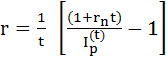(2.20)

! Пример. Начисление процентов в условиях инфляции

Определить годовой индекс инфляции (индекс цен), если известен квартальный темп инфляции равный, соответственно: 3%, 4%, 3.5%, 4,5%.

Решение.

Годовой индекс инфляции равен

I⁽¹⁾_p = ∏ (1+ h_k) = (1+ 0.03) (1+ 0.04) (1+ 0.035) (1+ 0.045) = 1,1586 (115,86 %).

_k=1

! Пример. Начисление процентов в условиях инфляции

На сумму в 5 000 руб. в течение трех месяцев начислялись простые проценты по ставке 40% годовых. За каждый месяц цены росли соответственно на 15, 12 и 10%. Найти наращенную сумму с учетом инфляции и величину положительной процентной ставки.

Решение.

1) Квартальный индекс инфляции равен

I⁽^t⁾_p = I⁽^t₁⁾_p ∙ I⁽^t₂⁾_p ∙ … ∙ I⁽^t_k⁾_p

I^(0,25)_p = 1,15 ∙ 1,12 ∙ 1,1 = 1,4168

2) Наращенную сумму с учетом инфляции определим по формуле (2.17)

5000· (1+0,4 ∙ 0,25)

FV^* = = 3882 руб.

1,4168

3) Найдем минимально допустимую ставку r^* при которой не происходит эрозии капитала

1,4168 - 1

r^* = = 1,6672 (166,72%).

0,25

Положительная процентная ставка, если r>166,72%

Операции с девизами

Девизы - это платежные средства выраженные в иностранной валюте. В процессе работы с этими средствами устанавливается обменный и девизный курсы.

Обменный курс - показывает сколько ед. отечественной валюты можно получить за 1 ед. иностранной валюты.

Девизный курс показывает сколько ед. иностранной валюты можно получить за 1 ед. отечественной валюты.

Если есть возможность конвертации валюты, т.е. обмена рублевых средств на иностранную валюту, то возникает ряд задач оптимизации ссудо-заемных операций с отечественной и иностранной валютой.

2.9.1 Рассмотрим финансовую операцию для наращения по процентной ставке "продажа СКВ - наращение по процентной ставке в рублях - покупка СКВ"

Обмен СКВ (в количестве PV^' единиц по курсу K₀) на рубли (в количестве PV единиц), затем наращение рублевой суммы по процентной ставке r до величины FV единиц за время t и конвертация наращенной суммы в СКВ в размере FV^’ единиц по курсу K_t.

Математически данную операцию можно записать в виде:

PV = PV^' ∙ K₀ ; FV= PV ( 1 + r ∙ t ) ; FV^' = FV / K_t.

Нетрудно преобразовать эту операцию к виду, позволяющему из начальной суммы PV^'в СКВ получить наращенное значение FV^'в СКВ.

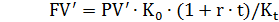(2.29)

Пусть известна процентная ставка r^'то по депозиту в СКВ, то за время t происходит наращение некоторой суммы в СКВ от значения PV^' до значения FV^', т.е.

FV^' = PV^' ( 1+ r^' ∙ t). (2.30)

Пусть неизвестен валютный курс в конце операции K_t при известных прочих параметрах: K₀, t, r, r^'. Выясним, при каких значениях K_t финансовые операции описываемые функциями (2.29) и (2.30) равнозначны или одна имеет преимущество по отношению к другой.

1) Определим параметры равнозначности финансовых операций описываемых функциями (2.29) и (2.30). Приравняем функции и получим

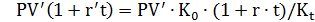
или

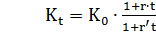(2.31)

2) Для того, чтобы приведенная выше финансовая операция с двойной конвертацией СКВ была предпочтительнее депозита в СКВ должно выполнятся неравенство

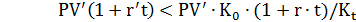или

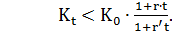(2.32)

3) Для того, чтобы депозит в СКВ был предпочтительнее приведенной выше финансовой операция с двойной конвертацией СКВ, должно выполнятся неравенство

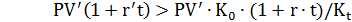или

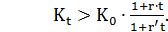(2.33)

! Пример. Конверсия валюты и начисление процентов

Вкладчик собирается поместить в банке 2000 единиц СКВ на рублевом депозите сроком на полгода под 14% годовых. Курс продажи СКВ на начало срока 27,7 руб., ожидаемый курс покупки через полгода 28,2 руб. Процентная ставка по СКВ депозиту – 11% годовых. При любом депозите начисляются простые проценты. Найти наращенную сумму: а) при конвертации валюты, б) непосредственно на валютном депозите. Выяснить максимальное значение курса, выше которого нет смысла в конвертации при помещении денежных средств на депозит.

Решение.

1) Определим будущую стоимость депозита с конвертацией (2.29) и без конвертации (2.30):

А) FV¹ = 2000 ∙27,7∙ (1+0,14 ∙0,5) / 28,2 = 2102,06 СКВ.

Б) FV_СКВ= 2000∙ (1+0,11 ∙0,5) = 2110 СКВ.

При курсе покупки СКВ K_t = 28,2 схема с конвертацией в рубли не имеет смысла.

2) Предельное значение курса K_t_, при котором обе операции равнозначны (2.31) будет

K_t = 27,7 (1+0,14 ∙0,5) / (1+0,11 ∙0,5) = 27,7 ∙ 1,07 / 1,055 = 28,09 руб.

При

K_t > 28,09 руб. нет смысла в приведенной выше схеме с конвертацией СКВ в рубли.

2.9.2 Рассмотрим финансовую операцию для наращения по процентной ставке "покупка СКВ - наращение по процентной ставке в СКВ - продажа СКВ"

Математически данную операцию с обозначениями, смысл которых описан при разборе первой схемы, можно записать в виде:

; ;

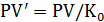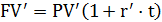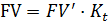
Нетрудно преобразовать эту операцию к виду позволяющему из начальной суммы PVвруб. получить наращенное значение FVв руб. зная курсы СКВ к рублю в начале K₀ и в конце K_t финансовой операции, а также процентную ставку r^’ по депозиту в СКВ и продолжительность t финансовой операции

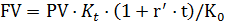(2.34)

Пусть известна процентная ставка r по депозиту в рублях по которой за время t происходит наращение некоторой суммы в руб. от величины PV до значения FV, т.е.

FV = PV ∙ (1 + r ∙ t ) (2.35)

Пусть неизвестен валютный курс в конце операции K_t при известных прочих параметрах: K₀, t, r, r^’. Выясним при каких значениях K_t финансовые операции описываемые функциями (2.34) и (2.35) равнозначны. или одна имеет преимущество по отношению к другой.

1) Определим параметры равнозначности финансовых операций описываемых функциями (2.34) и (2.35). Приравняем функции и получим

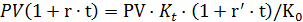или

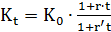(2.36)

2) Для того, чтобы приведенная выше финансовая операция с двойной конвертацией и наращением в СКВ была предпочтительнее депозита в рублях должно выполнятся неравенство

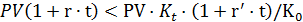или

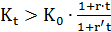(2.37)

3) Для того, чтобы депозит в рублях был предпочтительнее приведенной выше финансовой операции с двойной конвертацией и наращением в СКВ, должно выполнятся неравенство

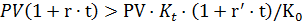или

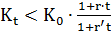(2.38)

Пример.

Клиент, имеет сумму в 30 тыс. руб., предполагает поместить ее на валютном депозите в СКВ на 9 мес. под 10% годовых. Выяснить целесообразность этой сделки с банком, если в начале срока СКВ можно купить по курсу 27,7 руб. и ожидается, что через 9 мес. СКВ можно продать по курсу 28,2 руб. Годовая процентная ставка на рублевом депозите – 20%.Проценты простые. Определить при каком курсе продажи схема с конвертацией в СКВ выгоднее простого депозита в рублях.

Решение.

Схема операции:

K₀ r¹ K_t

PV (Руб.) → PV¹ (СКВ.) → FV¹ (СКВ) → FV (Руб.)

1) Наращенная сумма по схеме с конвертацией (2.34)

FV = 30 ∙ 28,2 ∙ ( 1 + 0,1∙ 0,75) / 27,7 = 32,83 тыс. руб.

Наращенная сумма на рублевом депозите 2.(35)

FV = 30 ∙ ( 1 + 0,2∙ 0,75) = 34,5 тыс. руб.

При данных параметрах девизной операции наращение на рублевом депозите предпочтительнее, чем схема с конвертацией СКВ

2) При курсе, формула (2.37),

K_t > 27,7 ( 1 + 0,2∙ 0,75) / ( 1 + 0,1∙ 0,75) = 29,63 руб.,

схема с конвертацией будет выгоднее депозита в рублях

3. Основные формулы и примеры решения задач по теме «Теория процента. Сложный процент»

3.1 Основные формулы финансовых операций со сложными процентами при постоянных: процентной ставке и временном интервале

Инвестор размещает денежные средства PV в банке в начале некоторого года и получает доход в виде процентов по ставке r на протяжении t лет. Вклад сделан на условиях сложного процента, т.е. очередной годовой доход исчисляется с общей суммы включающей также и ранее начисленные проценты. В этом случае говорят, что происходит капитализация процентов. Следовательно, рост вклада на конец соответствующего года будет равен:

1 год: FV ₁= PV + PV ∙ r = PV ∙ ( 1 + r );

2 год: FV ₂= PV ∙( 1 + r ) + PV ∙ ( 1 + r ) ∙ r = PV ∙ ( 1 + r ) ² ;

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

t год: FV_t = PV ∙ ( 1 + r ) ^t^-1 + PV ∙ ( 1 + r ) ^t^-1∙ r = PV ∙ ( 1 + r ) ^t.

Очевидно, что доход вкладчика растет нелинейно из года в год.

Таким образом, в общем случае финансовой операции наращения по схеме сложного процента формула имеет вид

FV_t = PV ∙ (1 + r ) ^t = PV ∙ FM1( r, t ) , (3.1)

где t – срок инвестирования в годах;

r – годовая процентная ставка в долях единицы;

PV₀– начальная сумма инвестирования;

FV_t – наращенная сумма по истечении t лет.

FM1( r, t ) = (1 + r ) ^t - мультиплицирующий множитель для которого составлены финансовые таблицы или множитель наращения;

На практике многие финансовые операции выполняются в рамках одного или t лет, при m-кратном начислении процентов в год. В этом случае расчет ведется по формуле сложных процентов по периодам на которые разбит срок финансовой операции и по ставке равной годовой ставке r, деленной на число m периодов начислений

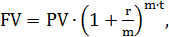(3.2)

где FV - сумма, получаемая при начислении процента за t лет;

PV – первоначально инвестированная сумма;

t – количество лет начисления процента ;

r - годовая процентная ставка в долях единицы;

m – число начислений в течении года.

Пример.

Начальная сумма 80 000 руб. инвестируется на 3 года под сложные проценты по ставке 35% годовых. Найдите наращенную сумму по истечении 3 лет.

Решение.

FV = 80 000 ∙ (1 + 0,35) ³ = 80 000 ∙ FM1( 35% , 3) = 80 000 ∙ 2,46 = 196 830 руб.

Пример.

Ссуда в 200 000 руб. дана на 1,5 года под ставку 40 % годовых с ежеквартальным начислением. Найти сумму конечного платежа.

Решение.

FV_1,5= 200000 ( 1 + 0.4 / 4 ) ^1,5^×⁴= 354312,20 руб.

3.2 Основные формулы финансовых операций со сложными процентами при переменных: процентной ставке и временном интервале

В практике финансовых расчетов, приходится часто изменять ставку сложных процентов особенно при значительных сроках ссудо-заемных операций. Пусть в начальный момент времени t₀=0 инвестор вложил в некоторый банк сумму PV. За время инвестиционного периода (t₀,t), изменение годовой процентной ставки происходило m раз на следующих временных интервалах:

t₁, t₂, t₃, … , t_m,

при чем на каждом интервале годовая процентная ставка оставалась постоянной и была равна соответственно:

r₁, r₂, r₃, … , r_m

В этом случае рост вклада к концу соответствующего временного интервала будет равен:

……………………………………………………………………….

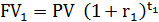
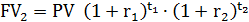
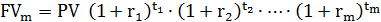Или искомую формулу можно записать в виде

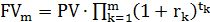. (3.3)

Пример.

На исходную сумму в 100000 руб. ежемесячно в течение квартала начисляются сложные проценты по ставке 10% в первый месяц, 11% во второй месяц и 12% в третий месяц. Найти наращенную сумму в конце квартала.

Решение.

FV_1/4 = 100000 (1+ 0,1) (1+0,11) (1+0,12) = 136752 руб.

Пример.

Банк предоставил кредит в размере 10 млн. руб. на 2 года. По условиям кредитного договора между банком и заемщиком устанавливается начисление сложных процентов при возврате кредита раз в полгода, при этом годовая процентная ставка меняется раз в полгода в следующей последовательности: 80%, 90%, 100% и 110% от ставки рефинансирования ЦБ. Найти сумму, которую получит банк по условиям кредитного договора, если ставки рефинансирования равна 10% и не меняется в течение действия кредитного договора.

Решение.

FV₂ = 10 (1+ 0,08/2) (1+0,09/2) (1+0,1/2) (1+0,11/2) = 12,03903 млн. руб.

Виды денежных потоков

Основой финансового анализа является оценка денежного потока (cash flow) с₁,с₂,...,с_n генерируемого в течение n временных периодов в результате реализации инвестиционного проекта или функционирования финансового актива. Будем полагать, что составляющие денежного потока с_i_:

1) однонаправленные (получение процентов по вкладу в банке, возврат кредита и др.);

2) составляющие потока сконцентрированы на границе периода.

Если составляющие потока c_i сконцентрированы в начале каждого периода, то этот поток называется пренумерандо (pre), если в конце, то поток называется постнумерандо (pst).

Аннуитет это денежный поток, в котором длительность всех периодов одинакова. Аннуитет называют также финансовой рентой.

Аннуитет называется постоянным если составляющие аннуитета постоянны с₁=с₂=,...,=с_n=с.

Задания для выполнения контрольной работы

Задание 1 . Темы «Процентные вычисления», «Потоки платежей». Задание выполняется с использованием методических рекомендаций по изучению дисциплины: Темы 2–4, учебных пособий из списка основной литературы [1; гл. 1, 2], [2; гл. 1, 2], учебного пособия, представленного в учебно-методическом комплексе (УМК) дисциплины:

Габескирия В.Я., Уродовских В.Н. Финансовая математика. Методические указания по выполнению лабораторной работы на ПЭВМ.

В задачах 1 – 17 выполнить различные коммерческие расчеты, используя данные, приведенные в таблице 1. Расчеты выполнить в среде Excel двумя способами:

1) с помощью математических формул и встроенных в Excel функций из категории «Математические»;

2) с помощью встроенных в Excel функций из категории «Дата и время» – ДОЛЯГОДА;

3) с помощью встроенных в Excel функций из категории «Финансовые» – БС, ПС, КПЕР, ЭФФЕКТ, НОМИНАЛ, ПЛТ и других.

Задача 1. Банк выдал ссуду размером Р рублей. Дата выдачи ссуды – Т_н, возврата – Т_к. День выдачи и день возврата считать за один день. Проценты рассчитываются по простой процентной ставке i% годовых.

Найти:

1) точные проценты с точным числом дней ссуды, обозначаемые как 365/365;

2) обыкновенные проценты с точным числом дней ссуды, обозначаемые как 365/360;

3) обыкновенные проценты с приближенным числом дней ссуды, обозначаемые как 360/360;

Задача 2. Сберегательный счет был открыт 3 января, и на него была положена сумма Р руб. Затем 20 марта со счета была снята сумма Р/5 руб., 20 апреля добавлена сумма в Р/10 руб. и 1 августа счет был закрыт. Все операции осуществлялись в течение года (простой год). Определить сумму полученную владельцем счета, если простая процентная ставка равнялась j% годовых и для начисления процентов применялся способ «365/360». Год обыкновенный.

Задача 3. Вкладчик разместил вначале года Р руб. в банке. Ставка рефинансирования ЦБ на момент заключения договора равна i % годовых. Договор предусматривает следующую схему начисления простых процентов: 1 квартал – 80% от ставки рефинансирования ЦБ, в каждом последующем квартале ставка понижается на 10% от ставки предыдущего квартала. Найти величину вклада через 1 год, если начисляются простые проценты.

Задача 4. Через Т_дн дней предприятие должно получить по векселю S рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке d% годовых (год равен 360 дням). Определить полученную предприятием сумму, дисконт и дисконтирующий множитель.

Задача 5. Платежи в S руб. и A руб. должны быть погашены соответственно через 150 и 300 дней. Кредитор и должник согласились заменить два платежа одним в сумме S+A руб. Найти срок оплаты консолидированного платежа, если используется простая процентная ставка i% и способ «360/360».

Задача 6. Инвестор, имеет сумму P руб., предполагает поместить ее на валютном депозите в СКВ на 9 мес. под i % годовых. Выяснить целесообразность этой сделки с банком, если в начале срока СКВ можно купить по курсу 27,7 руб. и ожидается, что через 9 мес. СКВ можно продать по курсу 28,2 руб. Годовая процентная ставка на рублевом депозите – (i+10)%. Проценты простые. Определить при каком курсе продажи схема с конвертацией в СКВ выгоднее простого депозита в рублях.

Задача 7. В кредитном договоре на сумму Р рублей и сроком на n лет зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную сумму и мультиплицирующий множитель. За сколько лет при ставке i% вклад вырастет в 3 раза?

Задача 8. Ссуда размером Р рублей представлена на n лет. Проценты сложные, ставка – j% годовых. Проценты начисляются m раз в году. Вычислить наращенную сумму. Определить срок, за который сумма Р удвоится при условиях данной задачи.

Задача 9. Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки j% годовых.

Задача 10. Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.

Задача 11. Через n лет предприятию будет выплачена сумме S рублей. Определить ее современную стоимость и дисконтирующий множитель при условии, что применяется сложная процентная ставка i% годовых.

Задача 12. Через n лет по векселю должна быть выплачена сумма S рублей. Банк учел вексель по сложной учетной ставке d% годовых. Определить дисконт.

Задача 13. На вклад P руб. ежемесячно начисляются сложные проценты по номинальной годовой процентной ставке j%. Оцените сумму вклада через 1,5 года с точки зрения эрозии капитала, если ожидаемый темп инфляции 0,5% в месяц. Какова должна быть величина положительной процентной ставки?

Задача 14. Три платежа P, 2·P и 3·P тыс. руб. со сроками выплат соответственно через 1 год, 2 года 6 месяцев и 3 года заменяются одним платежом, выплачиваемым через 2 года, при этом применяется сложная процентная ставка i% годовых. Найдите величину консолидированного платежа. Какой будет срок выплаты, если консолидированный платеж будет равен сумме исходных платежей?

Задача 15. Какую сумму необходимо поместить в банк под номинальную процентную ставку j% годовых, чтобы в течение n лет иметь возможность ежегодно получать R руб., снимая деньги равными долями каждые 3 месяца, и в конце n-го года исчерпать счет полностью, если банком начисляются сложные проценты m-раз в год.

Задача 16. В течение n лет на расчетный счет в конце каждого года поступает по R рублей, на которые m раз в году начисляются проценты по сложной годовой ставке j%. Определить сумму на расчетном счете к концу указанного срока для случаев ренты постнумерандо и пренумерандо.

Задача 17. Кредит в сумме А выдан на n лет по ставке сложных процентов j% годовых. Возврат кредита предполагается осуществлять в конце каждого месяца равными выплатами, включающими сумму основного долга и проценты. Определить вид потока платежей и найти величину погасительного платежа за месяц.

Таблица 1

Вариант	Р, A, R	S	T_н	Т_к	Т_дн	n	i, j, d	m
1	500000	10000000	23.01.2013	17.03.2013	180	2	8.0	12
2	1000000	9800000	24.01.2013	18.03.2013	180	3	8.5	12
3	1500000	9600000	30.01.2013	19.03.2013	180	4	9.0	2
4	2000000	9400000	31.01.2013	20.03.2013	180	10	9.5	2
5	2500000	9200000	01.02.2013	15.03.2013	180	11	10.0	2
6	3000000	9000000	28.01.2013	16.03.2013	90	12	10.5	4
7	3500000	8800000	29.01.2013	11.03.2013	90	8	11.0	4
8	4000000	8600000	25.01.2013	12.03.2013	90	9	11.5	2
9	4500000	8400000	27.01.2013	13.03.2013	90	5	12.0	12
10	5000000	8200000	26.01.2013	14.03.2013	90	6	12.5	4

Задание 2 . Тема «Анализ инвестиционных проектов». Задание выполняется с использованием методических рекомендаций по изучению дисциплины: Тема 5.

Решить задачу, используя данные, приведенные в таблице 1. Расчеты выполнить в среде Excel двумя способами:

1) с помощью математических формул и встроенных в Excel функций из категории «Математические»;

2) с помощью встроенных в Excel функций из категории «Финансовые» – ЧПС, ВСД.

Задача. Инвестиционный проект рассчитан на n лет и требует начальных инвестиций в размере S рублей. Денежные поступления прогнозируются в сумме S·k/n в каждом году (k = 1,…,n). Рассчитать приведенную стоимость проекта (NPV) и внутреннюю ставку доходности (IRR), если ставка дисконтирования равна d%. Сделать выводы.

Задание 3 . Тема «Портфель ценных бумаг». Задание выполняется с использованием лекции по Теме 6, учебных пособий [1; гл. 4], [2; гл. 4] из списка основной литературы.

Составить экономико-математические модели задач. Выполнить решение по формулам и с привлечением надстройки Excel «Поиск решений». Оптимальный портфель (доли ценных бумаг) представить в виде круговой диаграммы.

Вариант 1. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0,1;0.4), (0.2;0.6). Найти портфель минимального риска, его риск и доходность.

Вариант 2. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0.2;0.6) и (0.4;0,8). Найти портфель минимального риска, его риск и доходность.

Вариант 3. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0,1;0.5) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.

Вариант 4. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,1;0.5), (0.2;0.7) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.

Вариант 5. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,2;0.4), (0.3;0.6) и (0.5;0,8). Найти портфель минимального риска, его риск и доходность.

Вариант 6. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,1;0.5), (0.2;0.6) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.

Вариант 7. Необходимо сформулировать оптимальный портфель Марковица трех некоррелированных ценных бумаг с эффективностями и рисками: (4,20), (10,50), (40, 80). Нижняя граница доходности портфеля задана равной 15.

Вариант 8. Необходимо сформировать оптимальный портфель Марковица из трех некоррелированных ценных бумаг с эффективностями и рисками: (6,20), (12,50), (42, 80). Нижняя граница доходности портфеля задана равной 17.

Вариант 9. Сформировать портфель Тобина минимального риска из двух видов ценных бумаг: безрисковой с эффективностью 2 и рисковой с эффективностью 10 и риском 5. Доходность портфеля равна 8.

Вариант 10. Сформировать портфель Тобина минимального риска из трех видов ценных бумаг: безрисковой с эффективностью 2 и некоррелированных рисковых с ожидаемыми эффективностями 4 и 10 и рисками 2 и 4. Доходность портфеля равна 8.

Задание 4. Тема «Портфель ценных бумаг». Задание выполняется с использованием лекции по Теме 6 и файла Excel «Построение портфеля по статданным», учебных пособий [1; гл. 4], [2; гл. 4] из списка основной литературы.

Задача. Сформулировать и решить задачу на построение портфеля Марковица или Тобина, используя реальные данные о котировках цен на различные финансовые инструменты на фондовом рынке.

Задание 5 . Тема «Облигации». Задание выполняется с использованием лекции и практического занятия по Теме 3, учебных пособий [1; гл. 5], [2; гл. 5], из списка основной литературы.

В задачах 1 – 3 выполнить расчеты параметров облигаций, используя данные, приведенные в таблице 2. Расчеты выполнить в среде Excel двумя способами:

1) с помощью математических формул и встроенных в Excel функций из категории «Математические»;

2) с помощью встроенных в Excel функций из категории «Финансовые».

Задача 1. Номинал облигации равен N руб., купон выплачивается один раз в год по ставке – с%, до погашения остается n лет. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в r %. Определить текущую стоимость облигации.

Задача 2. Облигация со сроком погашения через n лет погашается по номиналу N руб. По облигации выплачивается ежегодный купонный доход в размере c% от номинала. Рыночная цена облигации составляет V руб. Определить доходность к погашению данной облигации. Сделайте выводы.

Задача 3. Номинал купонной облигации N руб., купон выплачивается один раз в год по ставке – c % годовых. До погашения облигации n лет, доходность до погашения составляет r%. Облигация торгуется по номиналу. Рассчитайте дюрацию Маколея для данной облигации. Сделайте выводы.

Таблица 2

Вариант	N	V	n	c	r
1	500	490	2	10.0	12.0
2	1000	950	3	9.0	11.0
3	1500	1480	4	8.5	10.0
4	2000	2100	5	8.0	13.0
5	2500	2600	6	7.5	14.0
6	3000	3150	5	7.0	12.0
7	3500	3400	4	6.5	11.5
8	4000	3950	3	6.0	11.0
9	4500	4400	2	5.5	10.5
10	5000	4900	2	5.0	10.0

Литература

а) основная:

1. Брусов П.Н. Финансовая математика: учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова, С.В. Скородулина. – 2-е изд., стер. – М.: КНОРУС, 2013 (библиотека филиала, ЭБС).

2. Брусов П. Н., Брусов П.П., Орехова Н.П., Скородулина С.В. Задачи по финансовой математике, Учебное пособие для бакалавров, Кнорус, 2013, 2014 (библиотека филиала, ЭБС).

б) дополнительная:

1. Брусов П. Н., Филатова Т. В. Финансовый менеджмент. Учебное пособие, том I– III. М.: Кнорус, 2012, 2013 (ЭБС).

2. Брусов П. Н., Филатова Т. В., Лахметкина Н.И. Инвестиционный менеджмент. Учебное пособие: Инфра–М, 2014 (ЭБС).

Электронные ресурсы

1. Интернет-репозиторий образовательных ресурсов. – URL: http://repozitory.vzfei.ru. Доступ по логину и паролю.

2. Электронно-библиотечная система (ЭБС) (доступ через интернет-репозиторий образовательных ресурсов). – URL: http://repozitory.vzfei.ru. Доступ по логину и паролю.

3. Федеральная ЭБС «Единое окно доступа к образовательным ресурсам». – URL: http://window.edu.ru. Доступ свободный.

Программное обеспечение

1. Электронная таблица Excel MS Office.

2. Программный продукт MatLab.

Содержание

Введение	3
1. Методические указания по выполнению и оформлению контрольной работы	3
2. Основные формулы и примеры решения задач по теме «Теория процента. Простой процент»	5
3. Основные формулы и примеры решения задач по теме «Теория процента. Сложный процент»	24
4. Основные формулы и примеры решения задач по теме «Финансовые потоки»	38
5. Анализ инвестиционных проектов	42
6. Задания для выполнения контрольной работы	45
Задание 1	45
Задание 2	48
Задание 3	49
Задание 4	50
Задание 5	51
7. Тематика творческих проектов	52
Учебно-методическое и информационное обеспечение	53

[1] Ста́вка рефинанси́рования — размер процентов в годовом исчислении, подлежащий уплате Центральному Банку страны за кредиты, которые центральный банк предоставил кредитным организациям.

ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»

Орловский филиал

Кафедра «Математика, информатика и общегуманитарные дисциплины»

Е.С. Филонова

Дата: 2019-04-22, просмотров: 626.

12 3 4 5 6 7 8 9 Следующая ⇒