Линейная модель множественной регрессии имеет вид:
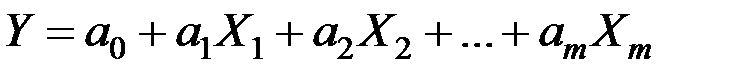 .
.
Для имеющихся исходных данных 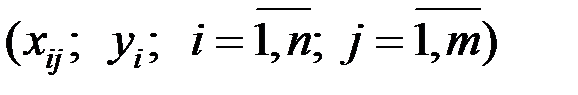 справедливо соотношение
справедливо соотношение
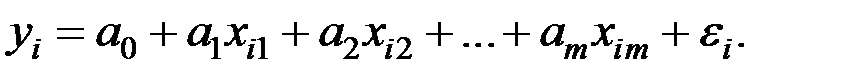
Неизвестные параметры 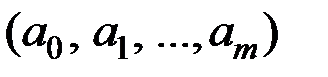 (случайные величины) оцениваются на основе выборочных наблюдений, поэтому полученные расчётные показатели не являются истинными, а представляют собой лишь их статистические оценки.
(случайные величины) оцениваются на основе выборочных наблюдений, поэтому полученные расчётные показатели не являются истинными, а представляют собой лишь их статистические оценки.
Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие модели регрессии и применяются на практике), имеет в матричном виде следующее соотношение:
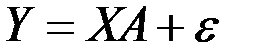 ,
,
где 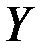 – вектор зависимой переменной размерности (п ´ 1), представляющий собой п наблюдений значений
– вектор зависимой переменной размерности (п ´ 1), представляющий собой п наблюдений значений 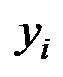 ;
;
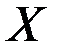 – матрица п наблюдений независимых переменных (Xl, X2, Х3, ..., Х m), размерность матрицы X равна п ´ (m + 1) (добавлен единичный столбец для определения а0);
– матрица п наблюдений независимых переменных (Xl, X2, Х3, ..., Х m), размерность матрицы X равна п ´ (m + 1) (добавлен единичный столбец для определения а0);
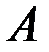 – подлежащий оцениванию вектор (матрица–столбец) неизвестных параметров размерности (m+1) ´ 1;
– подлежащий оцениванию вектор (матрица–столбец) неизвестных параметров размерности (m+1) ´ 1;
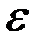 – вектор случайных отклонений (возмущений) размерности n ´ 1.
– вектор случайных отклонений (возмущений) размерности n ´ 1.
Таким образом, имеем следующие матрицы:
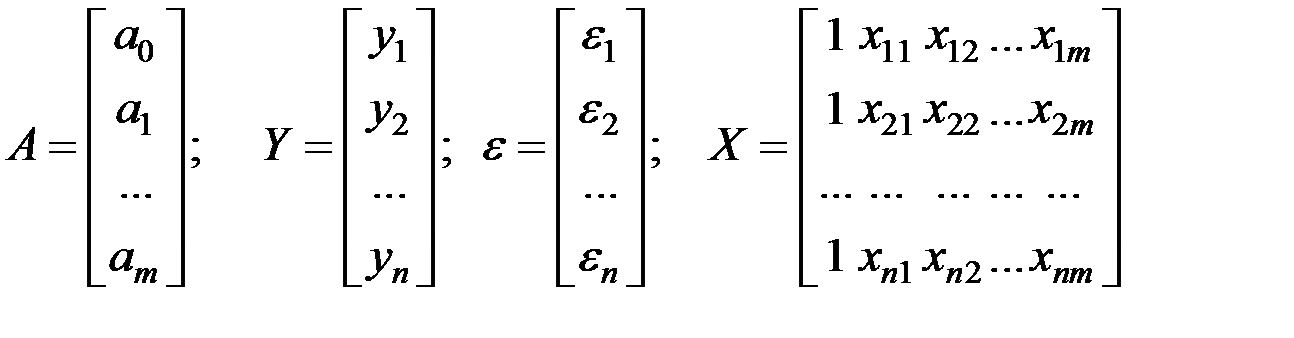 .
.
Неизвестные параметры определяются с помощью МНК.
При применении МНК делаются определённые предпосылки (условия Маркова–Гаусса).
1. Математическое ожидание остатков равно нулю: 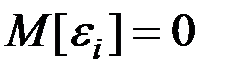 .
.
2. Дисперсия остатков постоянна для любого 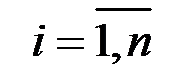 (условие гомоскедастичности), остатки
(условие гомоскедастичности), остатки 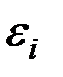 и
и 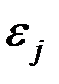 при
при 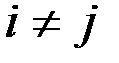 не коррелированы:
не коррелированы:
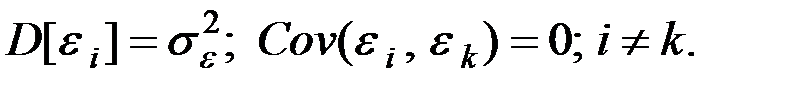
3. Ошибки 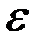 – нормально распределённый случайный вектор
– нормально распределённый случайный вектор
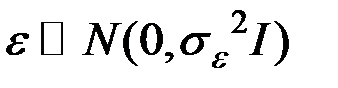
(здесь 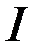 – единичная матрица).
– единичная матрица).
4. Столбцы матрицы X должны быть линейно независимыми, ранг матрицы X – максимальный (m + 1), а число наблюдений п превосходит ранг матрицы.
Модель, в которой зависимая переменная, остатки и объясняющие переменные удовлетворяют предпосылкам 1 – 4 называется классической нормальной моделью множественной регрессии.
Если не выполняется только предпосылка 3, то модель называется классической линейной моделью множественной регрессии.
Для имеющихся исходных данных 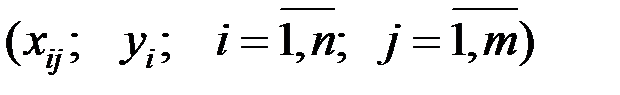 критерий МНК выглядит следующим образом:
критерий МНК выглядит следующим образом:
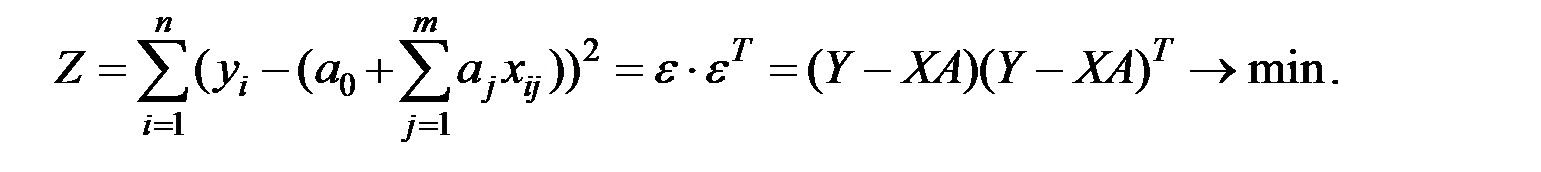
Здесь Т – символ транспонирования матрицы.
Для нахождения коэффициентов методом наименьших квадратов решаем систему линейных уравнений, которую получаем приравниванием частных производных к нулю:
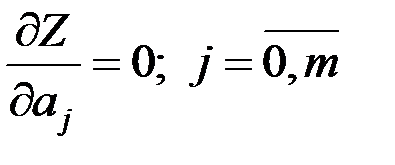 .
.
В матричном виде решение множественного регрессионного анализа определяется соотношением:
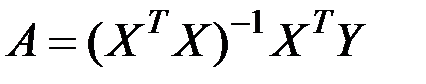 .
.
Для конкретного наблюдения имеем соотношение
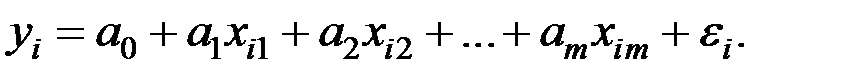
Коэффициент регрессии 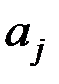 показывает, на какую величину в среднем изменится результативный признак
показывает, на какую величину в среднем изменится результативный признак 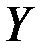 , если переменную
, если переменную 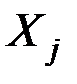 увеличить на одну единицу своего измерения при неизменном значении других факторов, закреплённых на среднем уровне (т.е.
увеличить на одну единицу своего измерения при неизменном значении других факторов, закреплённых на среднем уровне (т.е. 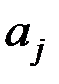 является нормативным коэффициентом, имеет размерность отношения размерностей
является нормативным коэффициентом, имеет размерность отношения размерностей 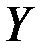 и
и 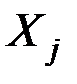 ).
).
Обычно предполагается, что случайная величина 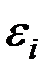 имеет нормальный закон распределения с математическим ожиданием равным нулю и некоторой дисперсией.
имеет нормальный закон распределения с математическим ожиданием равным нулю и некоторой дисперсией.
Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т.е., решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных линейно независимы. Для экономических показателей это условие выполняется не всегда.
Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели.
Мультиколлинеарность может возникать в силу разных причин.
Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания.
В частности, так может случиться, когда значения одной независимой переменной являются лагированными значениями другой.
Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причём тот, который в большей степени связан с зависимой переменной.
В качестве критерия отсутствия мультиколлинеарности может быть принято соблюдение следующих неравенств:
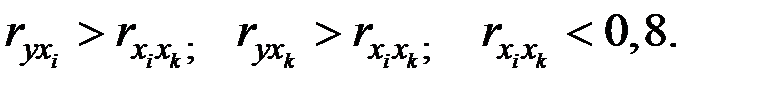
Если приведённые неравенства (или хотя бы одно из них) не выполняются, то в модель включают тот фактор, который наиболее тесно связан с 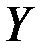 .
.
В условиях мультиколлинеарности исходных показателей обычные оценки МНК имеют высокие значения стандартных ошибок (оценки неустойчивы). В этом случае часто используются другие методы оценки параметров регрессии.
Дата: 2019-03-05, просмотров: 408.