Специальность
11.02.16 Монтаж, техническое обслуживание и ремонт
электронных приборов и устройств
Квалификация выпускника
специалист по электронным приборам и устройствам
Специальность
15.02.15 Технология металлообрабатывающего производства
Квалификация выпускника
техник
| Разработчик: Леонтьева Т.Ю., преподаватель |
2018
Фонд оценочных средств (далее – ФОС) по учебной дисциплине (далее – УД) ПД.01. Математика: алгебра, начала математического анализа, геометрия программы подготовки специалистов среднего звена (ППССЗ) по специальностям 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств и 15.02.15 Технология металлообрабатывающего производства базового уровня разработан на основе Федерального государственного образовательного стандарта (далее – ФГОС) по специальностям 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств и 15.02.15 Технология металлообрабатывающего производства в соответствии с рабочей программой учебной дисциплины ПД.01. Математика: алгебра, начала математического анализа, геометрия.
Разработчик (и):
МЦК "ЧЭМК"______ преподаватель__ Т.Ю. Леонтьева
(место работы) (занимаемая должность) (инициалы, фамилия)
__________________ ______________ ____________
(место работы) (занимаемая должность) (инициалы, фамилия)
СОГЛАСОВАНО
Председатель ЦК ________ ______________ ______________
(название ЦК) (подпись) (расшифровка подписи)
Содержание
- Область применения ФОС по учебной дисциплине ПД.01. Математика: алгебра, начала математического анализа, геометрия
- Программа текущего контроля успеваемости студентов
- ФОС для проведения текущего контроля
- Программа промежуточной аттестации студентов
- ФОС для промежуточной аттестации
1. Программа текущего контроля успеваемости студентов
по учебной дисциплине ПД.01. Математика: алгебра, начала математического анализа, геометрия
ФОС предназначен для проверки результатов освоения учебной дисциплины основной профессиональной образовательной программы (далее ОПОП) по специальностям 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств и 15.02.15 Технология металлообрабатывающего производства.
Текущий контроль освоения студентами материала учебной дисциплины Математика: алгебра и начала математического анализа, геометрия состоит из следующих видов: оперативный и рубежный контроль.
При проведении текущего контроля используются следующие формы (в скобках указан порядковый номер оценочного средства в структуре ФОС):
- аудиторная контрольная работа (3, 5, 7, 8, 10, 13, 15, 17, 19, 22);
- проверочная работа (2, 11, 14, 16);
- письменное тестирование (6, 12);
- индивидуальный опрос (1, 4, 9, 18, 20, 21, 23);
При проведении аудиторной контрольной работы студент прочитывает задания соответствующего варианта контрольной работы и отвечает письменно на вопросы (решает задания) в любом порядке. Время выполнения контрольной работы: 45 мин.
Проверочная работа в отличие от контрольной работы характеризуется меньшим охватом проверяемых тем (разделов) и меньшим временем, отведенным на ее выполнение в рамках аудиторного занятия (20-25 мин.).
При проведении письменного тестирования студенты должны внимательно прочитать задания теста и выбрать правильные ответы из предложенных вариантов. Если в тесте приведены задачи, то для выбора верного ответа студенту необходимо их решить. Количество правильных ответов и максимальное время прохождения теста указывается в задании в зависимости от темы и количества вопросов в тесте.
Индивидуальный опрос имеет своей целью основную проверку знаний и умений отдельных студентов. Студенты вызываются, как правило, к доске, хотя возможны ответы и с места, если не требуется записи, за которой должна следить группа, или использовать наглядные пособия и ТСО. При подготовке к индивидуальному опросу по предложенным преподавателем темам студентам необходимо руководствоваться рекомендациями к подготовке устного сообщения. В содержание ответа может включаться объяснение теоретического материала, выполнение практических заданий. При индивидуальном опросе обращается внимание на обстоятельный и осознанный ответ студента, логичность его суждений, доказательность выдвигаемых положений, умение практически применять усвоенные знания. Чрезвычайно важно привлечь внимание всех студентов группы к ответу товарища, обеспечить их активное участие в этой части урока, которая отведена опросу. Достигается это таким приемами, как постановка вопроса (или задания) всей группе, а затем вызов для ответа намеченного студента, привлечение всех студентов к комментированию отдельных положений, оригинальных способов выполнения упражнений и т.д. практически, таким образом, индивидуальный опрос сочетается с фронтальным.
ЛИЧНОСТНЫЕ
МЕТАПРЕДМЕТНЫЕ
ПРЕДМЕТНЫЕ
2. Комплект материалов для оценки уровня освоения умений и усвоения знаний при проведении текущего контроля учебной дисциплины
ОЦЕНОЧНОЕ СРЕДСТВО № 1
ОЦЕНОЧНОЕ СРЕДСТВО № 2
Вариант 1
- Вычислить:
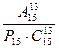 .
.
- В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?
- Записать разложение выражения (a+b)5 по формуле бинома Ньютона.
- Из букв слова «производная» наугад выбирается одна буква. Какова вероятность того, что эта буква окажется:
а) гласной;
б) согласной;
в) буквой «а»;
г) буквой «ж»?
Вариант 2
- Вычислить:
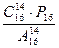 .
.
- Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
- Найти коэффициент бинома Ньютона для шестого члена разложения выражения (a+b)10.
- Из букв слова «интеграл» наугад выбирается одна буква. Какова вероятность того, что эта буква окажется:
а) гласной;
б) согласной;
в) буквой «а»;
г) буквой «ж»?
Пакет преподавателя
http://www.matburo.ru/ex_dm.php?p1=dmkomb


http://www.cleverstudents.ru/expressions/binomial_theorem.html

ОЦЕНОЧНОЕ СРЕДСТВО № 3
Вариант 1
- Найти
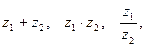 если
если 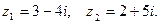
- Найти
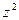 , если
, если 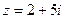 .
. - Представить в тригонометрической форме комплексное число
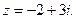
- Найти
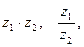 если
если 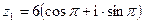 ,
, 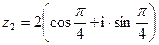 .
. - Найти
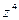 ,
, 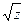 если
если 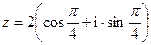 .
.
6. Решить уравнение 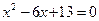 .
.
Вариант 2
- Найти
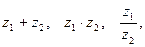 если
если 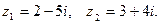
- Найти
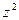 , если
, если 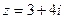 .
. - Представить в тригонометрической форме комплексное число
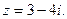
- Найти
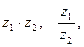 если
если 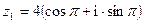 ,
, 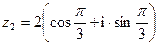 .
. - Найти
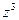 ,
, 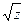 если
если 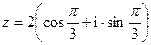 .
.
6. Решить уравнение 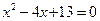 .
.
Вариант 3
- Найти
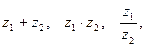 если
если 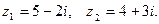
- Найти
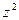 , если
, если 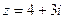 .
. - Представить в тригонометрической форме комплексное число
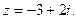
- Найти
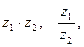 если
если 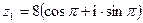 ,
, 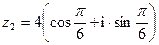 .
. - Найти
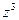 ,
, 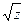 если
если 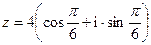 .
.
6. Решить уравнение 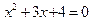 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 4
ОЦЕНОЧНОЕ СРЕДСТВО № 5
Вариант 1
№ 1. Решить уравнение с одной переменной 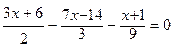 .
.
№ 2. Решить линейное неравенство 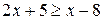 .
.
№ 3. Решить квадратное уравнение 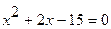 .
.
№ 4. Решить квадратное неравенство 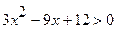 .
.
№ 5. Решить систему линейных неравенств 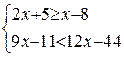 .
.
№ 6. Решить иррациональное уравнение 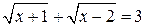 .
.
Вариант 2
№ 1. Решить уравнение с одной переменной 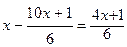 ;
;
№ 2. Решить линейное неравенство 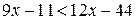 .
.
№ 3. Решить квадратное уравнение 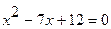 .
.
№ 4. Решить квадратное неравенство 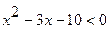 .
.
№ 5. Решить систему линейных неравенств 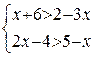 .
.
№ 6. Решить иррациональное уравнение 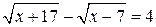 .
.
Пакет преподавателя
http://www.tutoronline.ru/blog/ne-boimsja-dokazyvat
http://unichance.ru/pages/32/?uid=1120
http://gigabaza.ru/doc/88972.html
ОЦЕНОЧНОЕ СРЕДСТВО № 6
Вариант 1
1. Найдите область определения функции 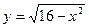 .
.
1) 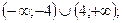
2) 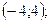
3) 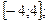
4) 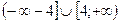 .
.
2. Найдите область значений функции 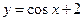 .
.
1) [-1;1];
2) [-2;2];
3) [0;2];
4) [1;3].
3. Проверьте функцию на четность 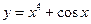 .
.
1) четная;
2) нечетная;
3) ни четная, ни нечетная;
4) периодическая.
4. Найдите нули функции 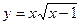 .
.
1) 0;
2) 1;
3) 0; 1;
4) нет.
5. По графику некоторой функции 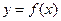 найдите промежутки возрастания.
найдите промежутки возрастания.
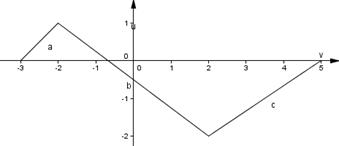 |
1) [-3;-2] U [2;5];
2) [-3;5];
3) [-2;2];
4) [2;5].
6. Найдите наименьший положительный период функции 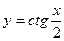 .
.
1) π;
2) 2 π;
3) 0,5 π;
4) 4 π.
7. Найдите наименьшее значение функции 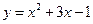 .
.
1) -1;
2) -3,25;
3) -1,5;
4) 1,25.
8. Укажите график функции 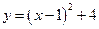 .
.
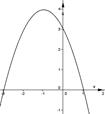 | |||
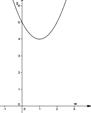 |
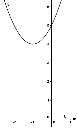
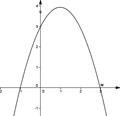
1) 2) 3) 4)
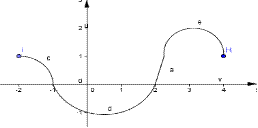
9. Найдите промежутки, на которых 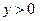 .
.
1) (-2;2);
2) [-2;0) U (2;4);
3) [-2;-1) U (2;4];
4) [0;3].
10. Дана функция 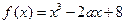 . Известно, что
. Известно, что 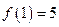 . Найдите
. Найдите 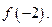
1) 16;
2) 0;
3) 8;
4) -8.
11. Укажите функцию, которой соответствует данный график.
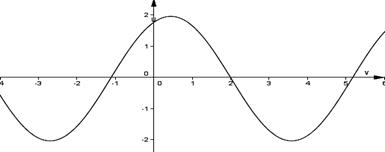 |
1) 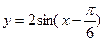 ;
;
2) 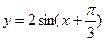 ;
;
3) 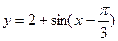 ;
;
4) 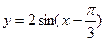 .
.
Вариант 2
1. Найдите область определения функции 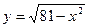 .
.
1) 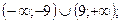
2) 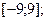
3) 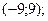
4) 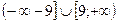 .
.
2. Найдите область значений функции у = sin x -2.
1) [-1:1];
2)[-3:-1];
3) (-2;0);
4) [-2;2].
3. Проверьте функцию на четность: 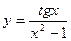 .
.
1) четная;
2) нечетная;
3) ни четная, ни нечетная;
4) убывающая.
4. Найдите нули функции 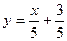 .
.
1) 3;
2) -3;
3) 0;
4) -5.
5. По графику некоторой функции 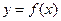 найдите промежутки возрастания.
найдите промежутки возрастания.
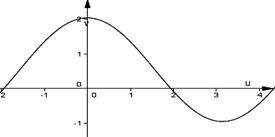 |
1) [-2;3] U [2;4];
2) [-3;5];
3) [0;3];
4) (-1;2).
6. Найдите наименьший положительный период функции 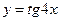 .
.
1) 2π;
2) 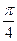 ;
;
3) 0,5 π;
4) 4 π.
7. Найдите наименьшее значение функции 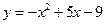 .
.
1) 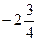 ;
;
2) -9;
3) 1,5;
4) 9,75.
8. Укажите график функции 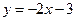 .
.
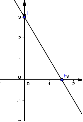

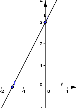
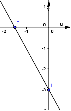 1) 2) 3) 4)
1) 2) 3) 4)
9. Найдите промежутки, на которых у<0.
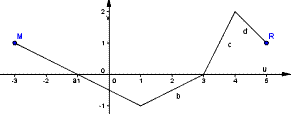 1) (-1;3);
1) (-1;3);
2) [-3;1]U[4;5];
3) (-3;-1);
4) [1;4].
10. Дана функция 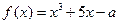 . Известно, что
. Известно, что 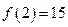 . Найдите
. Найдите 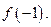
1) -3;
2) -9;
3) -8;
4) 0.
11. Укажите функцию, которой соответствует данный график.
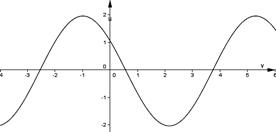
1) 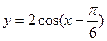 ;
;
2) 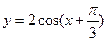 ;
;
3) 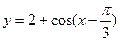 ;
;
4) 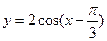 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 7
Вариант 1
1. Вычислить 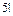 .
.
2. Из урны, в которой находятся 3 белых и 7 чёрных шаров, вынули один шар. Найдите вероятность того, что он окажется белым.
3. Решите уравнения: 1) 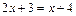 ;
;
2) 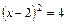 .
.
4. Решите неравенства: 1) 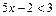 ;
;
2) 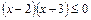 .
.
5. Постройте график функции: 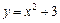 .
.
Вариант 2
1. Вычислить 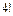 .
.
2. Из урны, в которой находятся 6 белых и 4 чёрных шаров, вынули один шар. Найдите вероятность того, что он окажется белым.
3. Решите уравнения: 1) 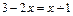 ;
;
2) 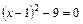 .
.
4. Решите неравенства: 1) 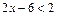 ;
;
2) 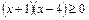 .
.
5. Постройте график функции: 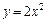 .
.
Вариант 3
1. Вычислить 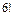 .
.
2. Из урны, в которой находятся 8 белых и 2 чёрных шара, вынули один шар. Найдите вероятность того, что он окажется чёрным.
3. Решите уравнения: 1) 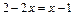 ;
;
2) 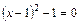 .
.
4. Решите неравенства: 1) 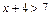 ;
;
2) 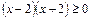 .
.
5. Постройте график функции: 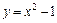 .
.
Оценка сложности: средней сложности
Вариант 1
1. Вычислить 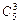 .
.
2. Из урны, в которой находятся 8 белых и 7 чёрных шаров, вынули один шар. Найдите вероятность того, что он окажется чёрным.
3. Решите уравнения: 1) 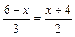 ;
;
2) 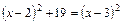 .
.
4. Решите неравенства: 1) 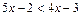 ;
;
2) 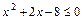 .
.
5. Найдите область определения и постройте график функции:
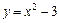 .
.
Вариант 2
1. Вычислить 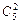 .
.
2. Из урны, в которой находятся 7 белых и 5 чёрных шаров, вынули один шар. Найдите вероятность того, что он окажется белым.
3. Решите уравнения: 1) 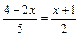 ;
;
2) 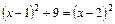 .
.
4. Решите неравенства: 1) 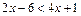 ;
;
2) 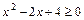 .
.
5. Найдите область определения и постройте график функции:
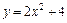 .
.
Вариант 3
1. Вычислить 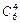 .
.
2. Из урны, в которой находятся 10 белых и 6 чёрных шаров, вынули один шар. Найдите вероятность того, что он окажется белым.
3. Решите уравнения: 1) 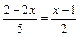 ;
;
2) 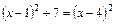 .
.
4. Решите неравенства: 1) 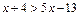 ;
;
2) 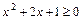 .
.
5. Найдите область определения и постройте график функции:
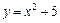 .
.
Оценка сложности: выше средней сложности
Вариант 1
1. Вычислить 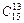 .
.
2. Считая выпадение любой грани игральной кости одинаково вероятным, найдите вероятность выпадения грани с нечетным числом очков.
3. Решите уравнения: 1) 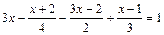 ;
;
2) 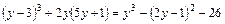 .
.
4. Решите неравенства: 1) 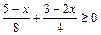 ;
;
2) 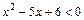 .
.
5. Найдите область определения и постройте график функции:
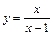 .
.
Вариант 2
1. Вычислить 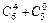 .
.
2. Считая выпадение любой грани игральной кости одинаково вероятным, найдите вероятность выпадения грани с нечетным числом очков.
3. Решите уравнения: 1) 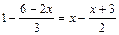 ;
;
2) 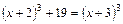 .
.
4. Решите неравенства: 1) 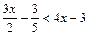 ;
;
2) 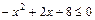 .
.
5. Найдите область определения и постройте график функции:
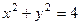 .
.
Вариант 3
1. Вычислить 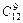 .
.
2. Считая выпадение любой грани игральной кости одинаково вероятным, найдите вероятность выпадения грани с четным числом очков.
3. Решите уравнения: 1) 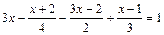 ;
;
2) 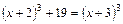 .
.
4. Решите неравенства: 1) 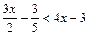 ;
;
2) 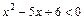 .
.
5. Найдите область определения и постройте график функции:
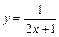 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 8
Вариант 1
1. Перечислить свойства функции и построить ее график:
а) 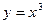 ;
;
б) 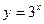 ;
;
в) 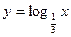 .
.
2. Сравнить:
а) 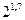 и
и 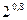 ;
;
б) 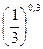 и
и 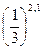 ;
;
в) 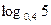 и
и 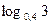 ;
;
г) 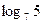 и
и 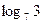 .
.
3. Решить уравнения:
а) 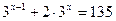 ;
;
б) 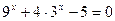 ;
;
в) 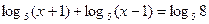 ;
;
г) 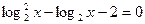 .
.
4. Решить неравенства:
а) 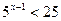 ;
;
б) 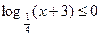 .
.
Вариант 2
1. Перечислить свойства функции и построить ее график:
а) 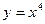 ;
;
б) 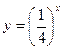 ;
;
в) 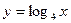 .
.
2. Сравнить:
а) 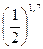 и
и 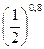 ;
;
б) 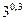 и
и 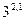 ;
;
в) 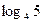 и
и 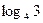 ;
;
г) 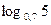 и
и 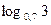 .
.
3. Решить уравнения:
а) 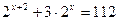 ;
;
б) 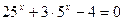 ;
;
в) 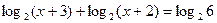 ;
;
г) 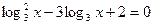 .
.
4. Решить неравенства:
а) 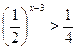 ;
;
б) 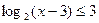 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 9
ОЦЕНОЧНОЕ СРЕДСТВО № 10
Вариант 1
1. Решить уравнение: 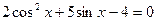 .
.
2. Решить уравнение: 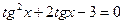 .
.
3. Решить уравнение: 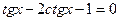 .
.
4. Решить уравнение: 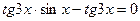 .
.
5. Решить уравнение: 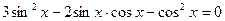 .
.
6. Решить уравнение: 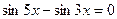 .
.
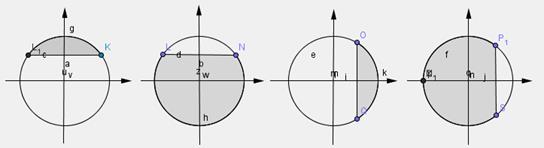
7. На каком из рисунков показано решение неравенства: 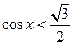 ?
?
1) 2) 3) 4)
 |
8. Решить неравенство: 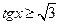 .
.
Вариант 2
1. Решить уравнение: 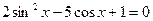 .
.
2. Решить уравнение: 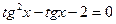 .
.
3. Решить уравнение: 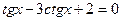 .
.
4. Решить уравнение: 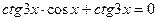 .
.
5. Решить уравнение: 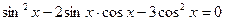 .
.
6. Решить уравнение: 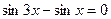 .
.
7. На каком из рисунков показано решение неравенства: sin x ≥ 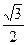 ?
?
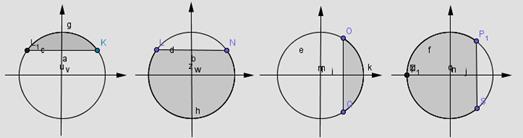 1) 2) 3) 4)
1) 2) 3) 4)
8. Решить неравенство: ctg x ≥ 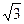 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 11
Вариант 1
1. Исследовать функцию 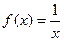 на непрерывность в точке
на непрерывность в точке 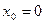 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 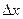 :
:
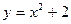 ,
, 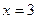 ,
, 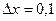 .
.
3. Сумма первого и четвертого членов убывающей геометрической прогрессии относится к сумме второго и третьего членов этой же прогрессии, как 13:4. Найти первый член прогрессии, если ее третий член равен 32.
Вариант 2
1. Исследовать функцию 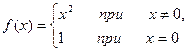 на непрерывность в точке
на непрерывность в точке 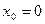 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 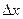 :
:
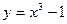 ,
, 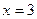 ,
, 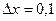 .
.
3. Сумма членов бесконечно убывающей геометрической прогрессии равна 56, а сумма квадратов ее членов равна 448. Найти эту прогрессию.
Вариант 3
1. Исследовать функцию 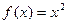 на непрерывность в точке
на непрерывность в точке 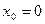 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 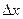 :
:
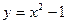 ,
, 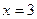 ,
, 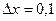 .
.
3. В квадрат, сторона которого равна 76 см, вписан другой квадрат, вершины которого являются серединами сторон первого квадрата, в этот квадрат вписан таким же образом другой квадрат и т.д. (см. рис.). Найти сумму площадей всех квадратов.

Пакет преподавателя
Вариант 1
1. Решение.
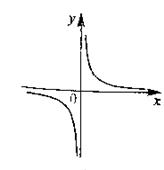
Проверим условия из определения.
1) 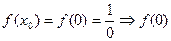 не существует, т. е. функция
не существует, т. е. функция 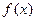 неопределенна в точке
неопределенна в точке 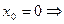 функция
функция 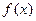 не является непрерывной в точке
не является непрерывной в точке 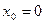 .
.
Ответ. Не является непрерывной.
Вариант 2
1. Решение.
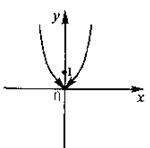
Проверим условия из определения.
1) 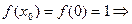 функция
функция 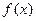 определенна в точке
определенна в точке 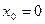 .
.
2) 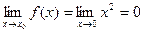 . Функция
. Функция 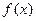 имеет конечный предел при
имеет конечный предел при 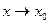 .
.
3) 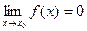 ,
, 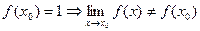 . Предел функции при
. Предел функции при 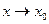 не равен значению функции в этой точке.
не равен значению функции в этой точке.
Ответ. Не является непрерывной.
Вариант 3
1. Решение.
Проверим условия из определения.
1) 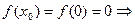 функция
функция 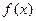 определенна в точке
определенна в точке 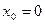 .
.
2) 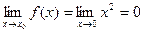 . Функция
. Функция 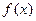 имеет конечный предел при
имеет конечный предел при 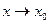 .
.
3) 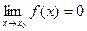 ,
, 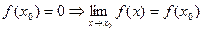 . Предел функции при
. Предел функции при 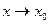 равен значению функции в этой точке.
равен значению функции в этой точке.
Ответ. Непрерывна.
http://www.yaklass.ru/p/algebra/9-klass/progressii-9139/geometricheskaia-progressiia-9142/re-f5f4ff72-963f-4b86-aece-3bb6086df8dc
ОЦЕНОЧНОЕ СРЕДСТВО № 12
Тема 4.2. Производная
1. Найдите производную функции f(x) = 4x-5.
a) 4 б) 9 в) -5
2. Найдите производную функции f(x) = 6x4-3x3-2x2-8.
а) 6х3-3х2-2х б) 24х3-9х2-2х2-8 в) 24х3-9х2-4х
3. Найдите производную функции f(x) = 5x3-4 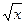 .
.
а) 15x2-4 б) 15x2- 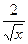 в) 15x2-
в) 15x2- 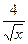
4. Найдите производную функции f(x) = 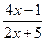 .
.
а) 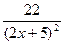 б)
б) 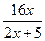 в)
в) 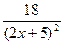
5. Найдите производную функции f(x) = xcosx.
а) cosx+xsinx б) sinx+xcosx в) cosx-xsinx
6. Найдите производную функции 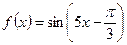 .
.
а) 5cos5x б) 5sin(x- 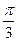 ) в) 5cos(5x-
) в) 5cos(5x- 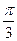 )
)
7. Найдите производную функции: f(x) = (1+3x)20.
а) (1+3x)19 б) 20(1+3х)19 в) 60(1+3х)19
8. Дана функция f(x) = x2-4x. Найдите значение производной в точке х = 4.
а) 12 б) 4 в) 8
9. Найдите 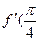 ), если f(x) = 3cosx.
), если f(x) = 3cosx.
а) 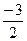
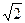 б)
б) 
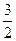
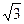 в)
в) 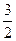
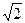
10. Найдите точки, в которых значение производной функции равно нулю.
a) х = -1; x = 7 б) x = -7; x = 1 в) 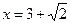 ; x = 3-
; x = 3- 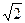

Пакет преподавателя
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| правильный ответ | а | в | б | а | а | в | в | б | а | а |
ОЦЕНОЧНОЕ СРЕДСТВО № 13
Тема 4.2. Производная
Вариант 1
1. Найти производную функции 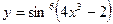 .
.
2. Найти производную третьего порядка функции 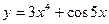 .
.
3. Написать уравнение касательной к графику функции 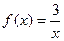 в точке с абсциссой
в точке с абсциссой 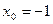 ,
, 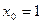 .
.
4. Материальная точка движется по закону 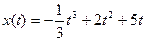 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Требуется огородить сеткой длиной 600 м зону отдыха прямоугольной формы, прилегающую к реке. Определить, каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь.
Вариант 2
1. Найти производную функции 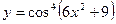 .
.
2. Найти производную третьего порядка функции 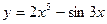 .
.
3. Написать уравнение касательной к графику функции 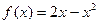 в точке с абсциссой
в точке с абсциссой 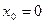 ,
, 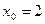 .
.
4. Материальная точка движется по закону 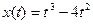 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Найти положительное число, которое, если сложить с обратным ему числом, даст наименьшую сумму.
Вариант 3
1. Найти производную функции 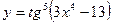 .
.
2. Найти производную третьего порядка функции 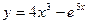 .
.
3. Написать уравнение касательной к графику функции 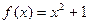 в точке с абсциссой
в точке с абсциссой 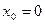 ,
, 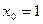 .
.
4. Материальная точка движется по закону 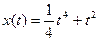 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Расходы на топливо на теплоходе пропорциональны кубу его скорости; при скорости 10 узлов (10 миль в час) расходы эти составляют 300 руб/ч. Остальные расходы составляют 4800 руб/ч. При какой скорости стоимость данного рейса будет наименьшей, если теплоход в состоянии развивать скорость до 18 узлов?
Вариант 4
1. Найти производную функции 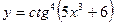 .
.
2. Найти производную третьего порядка функции 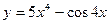 .
.
3. Написать уравнение касательной к графику функции 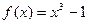 в точке с абсциссой
в точке с абсциссой 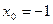 ,
, 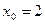 .
.
4. Материальная точка движется по закону 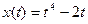 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Прямоугольный лист жести имеет длину 64 см и ширину 40 см. Из этого листа требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была максимальной?
Вариант 5
1. Найти производную функции 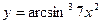 .
.
2. Найти производную третьего порядка функции 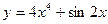 .
.
3. Написать уравнение касательной к графику функции 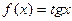 в точке с абсциссой
в точке с абсциссой 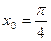 ,
, 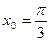 .
.
4. Материальная точка движется по закону 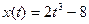 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Стадион представляет собой прямоугольное поле с областями в виде полукруга, присоединенными к двум его противоположным сторонам. Периметр стадиона должен быть равен 330 м. Найти наибольшую возможную его площадь.
Вариант 6
1. Найти производную функции 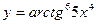 .
.
2. Найти производную третьего порядка функции 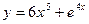 .
.
3. Написать уравнение касательной к графику функции 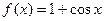 в точке с абсциссой
в точке с абсциссой 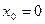 ,
, 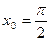 .
.
4. Материальная точка движется по закону 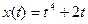 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
5. Расходы на топливо на теплоходе пропорциональны кубу его скорости; при скорости 10 узлов (10 миль в час) расходы эти составляют 300 руб/ч. Остальные расходы составляют 4800 руб/ч. При какой скорости стоимость данного рейса будет наименьшей, если предельная скорость теплохода 25 узлов?
Пакет преподавателя
Вариант 1
1. 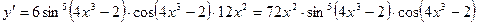 .
.
Вариант 2
1. 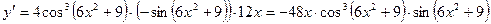 .
.
Вариант 3
1. 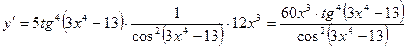 .
.
Вариант 4
1. 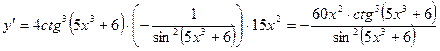 .
.
Вариант 5
1. 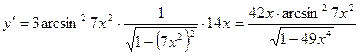 .
.
Вариант 6
1. 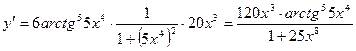 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 14
Тема 4.2. Производная
Справочный материал
По распространенному убеждению, в жизни человека чередуются черные и белые полосы. Если сегодня ты огорчен, тебя преследуют неудачи, самочувствие все ухудшается, то вскоре надо ждать какого-то просветления. Конечно, не всегда это так. Но некоторая закономерность все равно есть.
А чем же эти белые и черные полосы определяются? Одним словом, от чего на самом деле зависит наше состояние и самочувствие?
Огромную роль в жизни человека играют циклы. Цикличность – одно из самых главных свойств всего мироздания. Существуют циклы суточные, сезонные, годовые. Циклично движение солнца и планет солнечной системы. И вот около ста лет назад появилась теория «трех биоритмов».
Физический биоритм регулирует физическую активность, силу, скорость, координацию, выносливость. Примеры этого мы наблюдаем достаточно часто в повседневной жизни. Всякому футбольному болельщику известна сакраментальная фраза спортивных комментаторов, что у такого-то футболиста сегодня не идет игра. Как правило, это связано как раз с тем, в какой фазе физического биоритма находится данный игрок.
Эмоциональный биоритм влияет на накал эмоций, на остроту восприятия, на чувствительность. Все, наверное, замечали, что один и тот же человек иногда может проявить чуткость и понимание, а в какой-то другой ситуации остаться абсолютно равнодушным.
Интеллектуальный биоритм отвечает за умственные способности, ясность мышления, остроту памяти. С перепадами такого биоритма очень хорошо знакомы люди научного труда. Бывает, что в какие-то дни любая задача, даже самая сложная, решается на удивление легко. А случается, что на выполнении простейшей работы невозможно сосредоточиться и крайне трудно довести ее до конца.
Биоритм можно представить в виде синусоиды с периодом, равным циклу. В момент рождения человека синусоиды находятся в нуле (начале системы координат). Ритмичность физического цикла составляет 23 дня, психический цикл длится 28 дней, а интеллектуальный биоритм составляет 33 дня. По оси абсцисс располагаются даты, а переменная х означает прожитые человеком дни. Нижняя точка синусоиды называется минимумом, а высшая – максимумом. И если минимум обычно характеризуется упадком сил, вялостью, отсутствием положительных эмоций, то уж максимум позволяет человеку полностью раскрыть себя и все свои возможности. В каждом цикле два минимума и два максимума. Особенно важны минимумы. Может наступить такой момент, когда несколько минимумов совпадут. Вот это и называется в словесном обиходе «черными днями», когда все буквально валится из рук. Если какие-то даты пересекаются двумя или более синусоидами – это и есть критические дни. В некоторых странах людей опасных профессий (диспетчеров, пилотов, водителей) не допускают к работе, им дают выходной. Но если совпадут несколько максимумов, вы можете просто свернуть горы.
Математически физический цикл описывается функцией 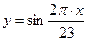 , эмоциональному циклу соответствует функция
, эмоциональному циклу соответствует функция 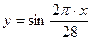 , а описание интеллектуального цикла соответствует формуле
, а описание интеллектуального цикла соответствует формуле 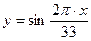 .
.
Вариант 1
1. Исследовать функцию и построить ее график: 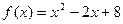 .
.
2. Построить график физического биоритма. Определить точки максимума. Выполнить анализ полученных результатов.
Вариант 2
1. Исследовать функцию и построить ее график: 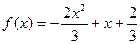 .
.
2. Построить график физического биоритма. Определить точки минимума. Выполнить анализ полученных результатов.
Вариант 3
1. Исследовать функцию и построить ее график: 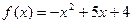 .
.
2. Построить график эмоционального биоритма. Определить точки максимума. Выполнить анализ полученных результатов.
Вариант 4
1. Исследовать функцию и построить ее график: 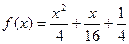 .
.
2. Построить график эмоционального биоритма. Определить точки минимума. Выполнить анализ полученных результатов.
Вариант 5
1. Исследовать функцию и построить ее график: 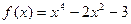 .
.
2. Построить график интеллектуального биоритма. Определить точки максимума. Выполнить анализ полученных результатов.
Вариант 6
1. Исследовать функцию и построить ее график: 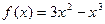 .
.
2. Построить график интеллектуального биоритма. Определить точки минимума. Выполнить анализ полученных результатов.
ОЦЕНОЧНОЕ СРЕДСТВО № 15
ОЦЕНОЧНОЕ СРЕДСТВО № 16
Раздел 5. Геометрия.
Вариант 1
- Выполните чертеж к задаче. Прямые а, в, и с имеют общую точку О, но не существует плоскости, в которой лежат все эти три точки.
- Выполните чертеж к задаче. Плоскость α проходит через середины сторон АВ и АС ΔАВС и не содержит вершины А.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если точка О середина АВ.
Вариант 2
- Выполните чертеж к задаче. Прямые а, в, и с имеют общую точку О и лежат в одной плоскости.
- Выполните чертеж к задаче. Прямая а параллельна каждой из параллельных плоскостей α и β.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если точка В середина ОА.
Вариант 3
- Выполните чертеж к задаче. Прямые СД и СК пересекают плоскость β в разных точках.
- Выполните чертеж к задаче. Прямая АВ параллельна плоскости γ, а прямая АТ пересекает ее в точке Т.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если точка А средина ОВ.
Вариант 4
- Выполните чертеж к задаче. Две вершины ΔАВС лежат в плоскости γ, а вершина С не лежит в плоскости γ. Прямая d пересекает стороны СВ и СК соответственно в точках М и Т, а плоскость α в точке К.
- Выполните чертеж к задаче. Плоскость α пересекает три параллельных прямых соответственно в точках А, В, и С, лежащих на одной прямой.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если ОА = 8 см, АВ = 6 см.
ОЦЕНОЧНОЕ СРЕДСТВО № 17
Раздел 5. Геометрия.
Вариант 1
1. Даны два вектора 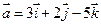 и
и 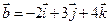 . Вычислить координаты и длину векторов
. Вычислить координаты и длину векторов 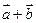 и
и 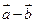 .
.
2. Найти площадь треугольника по координатам его вершин: 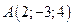 ,
, 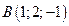 и
и 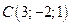 .
.
3. Даны векторы 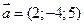 и
и 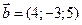 . Вычислить косинус угла между ними.
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов 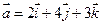 и
и 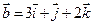 .
.
5. Даны векторы 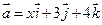 и
и 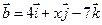 . При каком значении
. При каком значении 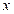 векторы
векторы 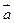 и
и 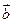 перпендикулярны?
перпендикулярны?
6. Вектор 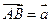 задан координатами своих концов:
задан координатами своих концов: 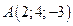 ,
, 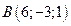 . Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами
. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 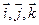 .
.
Вариант 2
1. Даны два вектора 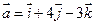 и
и 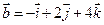 . Вычислить координаты и длину векторов
. Вычислить координаты и длину векторов 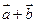 и
и 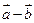 .
.
2. Найти площадь треугольника по координатам его вершин: 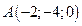 ,
, 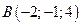 и
и 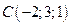 .
.
3. Даны векторы 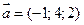 и
и 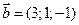 . Вычислить косинус угла между ними.
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов 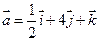 и
и 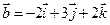 .
.
5. Даны векторы 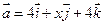 и
и 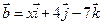 . При каком значении
. При каком значении 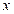 векторы
векторы 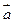 и
и 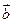 перпендикулярны?
перпендикулярны?
6. Вектор 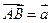 задан координатами своих концов:
задан координатами своих концов: 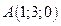 ,
, 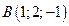 . Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами
. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 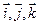 .
.
Вариант 3
1. Даны два вектора 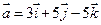 и
и 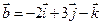 . Вычислить координаты и длину векторов
. Вычислить координаты и длину векторов 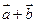 и
и 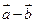 .
.
2. Найти площадь треугольника по координатам его вершин: 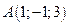 ,
, 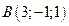 и
и 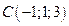 .
.
3. Даны векторы 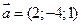 и
и 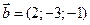 . Вычислить косинус угла между ними.
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов 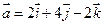 и
и 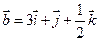 .
.
5. Даны векторы 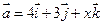 и
и 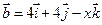 . При каком значении
. При каком значении 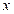 векторы
векторы 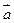 и
и 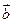 перпендикулярны?
перпендикулярны?
6. Вектор 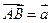 задан координатами своих концов:
задан координатами своих концов: 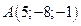 ,
, 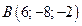 . Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами
. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 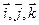 .
.
Вариант 4
1. Даны два вектора 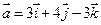 и
и 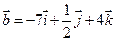 . Вычислить координаты и длину векторов
. Вычислить координаты и длину векторов 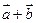 и
и 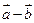 .
.
2. Найти площадь треугольника по координатам его вершин: 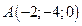 ,
, 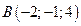 и
и 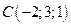 .
.
3. Даны векторы 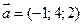 и
и 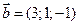 . Вычислить косинус угла между ними.
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов 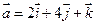 и
и 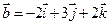 .
.
5. Даны векторы 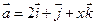 и
и 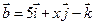 . При каком значении
. При каком значении 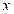 векторы
векторы 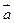 и
и 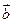 перпендикулярны?
перпендикулярны?
6. Вектор 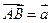 задан координатами своих концов:
задан координатами своих концов: 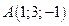 ,
, 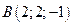 . Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами
. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 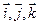 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 18
Раздел 5. Геометрия.
ОЦЕНОЧНОЕ СРЕДСТВО № 19
Раздел 5. Геометрия.
Тема 5.3. Многогранники


ОЦЕНОЧНОЕ СРЕДСТВО № 20
Раздел 5. Геометрия.
ОЦЕНОЧНОЕ СРЕДСТВО № 21
Раздел 5. Геометрия.
ОЦЕНОЧНОЕ СРЕДСТВО № 22
Раздел 5. Геометрия.
Вариант 1
- Площадь осевого сечения цилиндра равна 24 см2, высота цилиндра равна 6 см. Найти объем цилиндра.
- В правильной четырехугольной пирамиде сторона основания 5 м, апофема 6 м. Найти боковую и полную поверхности пирамиды.
- Сфера задана уравнением:
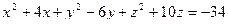 . Необходимо: а) привести уравнение сферы к общему виду; б) найти площадь этой сферы; в) найти объем шара, ограниченного этой сферой.
. Необходимо: а) привести уравнение сферы к общему виду; б) найти площадь этой сферы; в) найти объем шара, ограниченного этой сферой. - Диаметры оснований усеченного конуса равны 6 и 10 см, его образующая наклонена к плоскости основания под углом 450. Найти: а) площадь боковой поверхности; б) площадь полной поверхности; в) объем этого конуса.
Вариант 2
- Осевое сечение конуса – равнобедренный треугольник с основанием 8 см и боковой стороной 5 см. Найти объем конуса.
- В правильной четырехугольной призме сторона основания 4 м, боковое ребро 7 м. Найти боковую и полную поверхности призмы.
- Сфера задана уравнением:
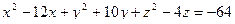 . Необходимо: а) привести уравнение сферы к общему виду; б) найти площадь этой сферы; в) найти объем шара, ограниченного этой сферой.
. Необходимо: а) привести уравнение сферы к общему виду; б) найти площадь этой сферы; в) найти объем шара, ограниченного этой сферой. - В правильной усеченной четырехугольной пирамиде стороны верхнего и нижнего оснований равны 6 и 10 см, двугранный угол при ребре нижнего основания равен 450. Найти: а) площадь боковой поверхности; б) площадь полной поверхности; в) объем этой пирамиды.
ОЦЕНОЧНОЕ СРЕДСТВО № 23
Раздел 5. Геометрия.
ПРЕДМЕТНЫЕ
4. Комплект материалов для оценки уровня освоения умений и усвоения знаний, при проведении промежуточной аттестации учебной дисциплины ПД.01. Математика: алгебра, начала математического анализа, геометрия
ОЦЕНОЧНОЕ СРЕДСТВО № 24
Зимняя сессия
1. Основные понятия комбинаторики. Перестановки, размещения, сочетания. Треугольник Паскаля. Бином Ньютона, свойства биноминальных коэффициентов. Формулы сокращенного умножения для старших степеней.
2. Событие. Вероятность события.
3. Натуральные, целые и рациональные числа. Десятичные дроби. Иррациональные числа. Действительные числа.
4. Комплексные числа. Действительная и мнимая часть, модуль и аргумент комплексного числа. Равные комплексные числа. Комплексно-сопряженные числа. Геометрическая интерпретация комплексных чисел. Решение квадратных уравнений при отрицательном дискриминанте.
5. Действия над комплексными числами в алгебраической форме. Степени мнимой единицы.
6. Полярные координаты точки на плоскости. Соотношения, связывающие полярные и прямоугольные координаты. Тригонометрическая форма комплексного числа. Переход от алгебраической формы записи комплексного числа к тригонометрической и обратно. Действия над комплексными числами, заданными в тригонометрической форме.
7. Числовая функция. Область определения и множество значений функции. Способы задания функции. График функции.
8. Монотонность, ограниченность, четность и нечетность, периодичность функции.
9. Преобразования графиков функций: построение графиков функций 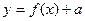 ,
, 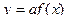 ,
, 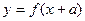 ,
, 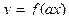 .
.
10. Обратные функции. Область определения и множество значений обратной функции. График обратной функции.
11. Корень натуральной степени из числа и его свойства.
12. Степень с рациональным показателем, степень с действительным показателем и их свойства.
13. Логарифм числа. Основное логарифмическое тождество. Логарифмирование. Десятичный логарифм. Натуральный логарифм. Число е.
14. Основные свойства логарифмов. Формула перехода от одного основания логарифма к другому основанию.
15. Степенная функция, ее свойства и график.
16. Показательная функция, ее свойства и график.
17. Логарифмическая функция, ее свойства и график.
18. Радианная мера угла. Соотношения между градусной и радианной мерами угла. Синус, косинус, тангенс, котангенс острого угла и прямоугольный треугольник. Тригонометрические функции числового аргумента.
19. Знаки, периодичность, четность и нечетность тригонометрических функций. Основные тригонометрические тождества. Значения тригонометрических функций для некоторых углов.
20. Формулы приведения.
21. Формулы сложения. Формулы суммы и разности одноименных тригонометрических функций.
22. Формулы двойного и половинного аргументов.
23. Функция 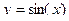 , ее свойства и график.
, ее свойства и график.
24. Функция 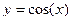 , ее свойства и график.
, ее свойства и график.
25. Функция 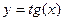 , ее свойства и график.
, ее свойства и график.
26. Функция 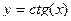 , ее свойства и график.
, ее свойства и график.
27. Арксинус, арккосинус, арктангенс, арккотангенс числа.
28. Функция арксинус, ее свойства и график. Функция арктангенс, ее свойства и график.
29. Функция арккосинус, ее свойства и график. Функция арккотангенс, ее свойства и график.
30. Простейшие тригонометрические уравнения, их решение.
ОЦЕНОЧНОЕ СРЕДСТВО № 25
Летняя сессия
1. Числовая последовательность. Способы задания числовой последовательности. Предел числовой последовательности. Число е.
2. Приращение аргумента и приращение функции. Понятие производной функции. Таблица производных. Сложная функция. Производная сложной функции.
3. Касательная к графику функции, ее уравнение. Геометрический смысл производной. Нормаль, угловой коэффициент нормали.
4. Производные высших порядков. Физический смысл первой и второй производной.
5. Теорема Вейерштрасса. Правило нахождения наибольшего и наименьшего значений функции.
6. Возрастающая и убывающая функции. Признак возрастания и убывания функции. Правило нахождения промежутков монотонности функции. Точки экстремума и экстремумы функции. Правило нахождения экстремумов функции.
7. Выпуклость и вогнутость кривой. Точки перегиба. Правило нахождения точек перегиба.
8. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов.
9. Определенный интеграл, его основные свойства. Формула Ньютона-Лейбница. Геометрический и физический смысл определенного интеграла.
10. Аксиомы стереометрии и их простейшие следствия.
11. Взаимное расположение прямых в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые. Признак скрещивающихся прямых.
12. Взаимное расположение прямой и плоскости. Параллельность прямой и плоскости.
13. Взаимное расположение двух плоскостей. Параллельность плоскостей.
14. Перпендикулярность скрещивающихся прямых. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости. Перпендикуляр и наклонная. Два перпендикуляра к плоскости. Перпендикуляр к двум плоскостям. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Расстояние от точки до плоскости.
15. Двугранный угол и его измерение. Угол между плоскостями. Перпендикулярные плоскости. Признак перпендикулярности двух плоскостей.
16. Параллельная проекция и ее свойства. Ортогональная проекция и ее свойства. Симметрия относительно плоскости. Изображение пространственных фигур. Площадь проекции плоской фигуры.
17. Скалярные и векторные величины. Вектор. Модуль вектора. Нулевой вектор. Равные векторы. Одинаково направленные и противонаправленные векторы. Единичный вектор. Орт. Угол между двумя векторами. Ортогональные векторы. Противоположные векторы.
18. Сложение векторов. Правило треугольника, правило параллелограмма, правило многоугольника. Вычитание векторов. Умножение вектора на число.
19. Коллинеарные векторы, признак коллинеарности векторов. Разложение вектора на плоскости по двум неколлинеарным векторам. Координаты вектора. Прямоугольная система координат на плоскости.
20. Компланарные векторы, правило параллелепипеда. Разложение вектора в пространстве по трем некомпланарным векторам. Координаты вектора. Прямоугольная система координат в пространстве.
21. Действия над векторами, заданными своими координатами: сложение, вычитание векторов, умножение вектора на число. Нахождение координат вектора по координатам его начала и конца. Длина вектора. Формула расстояния между двумя точками. Скалярное произведение двух векторов. Необходимое и достаточное условие взаимной перпендикулярности двух векторов. Скалярный квадрат вектора. Скалярное умножение векторов. Нахождение угла между векторами.
22. Уравнение окружности. Уравнение сферы. Уравнение прямой. Уравнение плоскости.
23. Многогранные углы. Многогранная поверхность. Многогранник. Развертка. Сечение многогранника. Основные правила построения сечений. Сечения пирамиды и параллелепипеда.
24. Призма. Прямая и наклонная призма. Правильная призма. Перпендикулярное сечение призмы. Параллелепипед. Наклонный, прямой, прямоугольный параллелепипед. Измерения прямоугольного параллелепипеда. Куб, измерения куба. Площадь поверхности призмы. Объем призмы, прямоугольного и наклонного параллелепипеда, куба.
25. Пирамида. Правильная пирамида. Усеченная пирамида. Правильная усеченная пирамида. Апофема. Площадь поверхности пирамиды и усеченной пирамиды. Объем пирамиды и усеченной пирамиды.
26. Правильные многогранники, их свойства и развертки.
27. Цилиндр. Сечения цилиндра плоскостями. Вписанная и описанная призмы. Площадь поверхности цилиндра. Объем цилиндра.
28. Конус. Сечения конуса плоскостями. Усеченный конус. Вписанная и описанная пирамиды. Площадь поверхности конуса и усеченного конуса. Объем конуса и усеченного конуса.
29. Сфера. Шар и его части. Площадь сферы. Объем шара. Плоскость, касательная к сфере. Вписанные и описанные многогранники.
30. Понятие об объеме пространственного тела. Свойства объема. Интегральная формула объема. Равновеликие тела.
ОЦЕНОЧНОЕ СРЕДСТВО № 26
ПЕРЕЧЕНЬ ЗАДАЧ ДЛЯ ЭКЗАМЕНА
Часть 1
1. Доказать равенство:
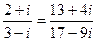 .
.
2. Решить следующее логарифмическое неравенство:
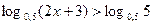 .
.
3. Решить квадратное уравнение во множестве комплексных чисел:
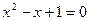 .
.
4. Найти значение числового выражения:
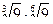 .
.
5. Исследовать функцию 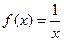 ,
, 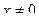 , на четность и нечетность.
, на четность и нечетность.
6. Найти значение числового выражения:
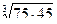 .
.
7. Найти значение числового выражения:
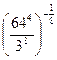 .
.
8. Решить следующее логарифмическое неравенство:
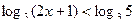 .
.
9. Решить следующее логарифмическое уравнение:
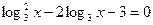 .
.
10. Вычислить:
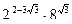 .
.
11. Решить следующее показательное уравнение:
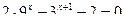 .
.
12. Вычислить:
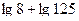 .
.
13. Вычислить:
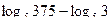 .
.
14. Решить следующее показательное уравнение:
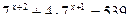 .
.
15. Решить следующее показательное неравенство:
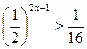 .
.
16. Вычислить:
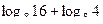 .
.
17. Найти область определения функции 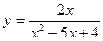 .
.
18. Вычислить:
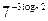 .
.
19. Вычислить:
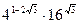 .
.
20. Исследовать функцию 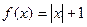 на четность и нечетность.
на четность и нечетность.
21. Найти обратную функцию для функции 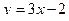 .
.
22. Решить следующее показательное уравнение:
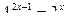 .
.
23. Найти область определения функции 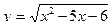 .
.
24. Решить следующее показательное уравнение:
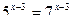 .
.
25. Решить следующее показательное неравенство:
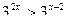 .
.
26. Решить следующее логарифмическое уравнение:
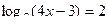 .
.
27. Решить следующее логарифмическое уравнение:
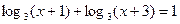 .
.
28. Решить квадратное неравенство:
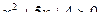 .
.
29. Решить квадратное неравенство:
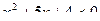 .
.
30. С помощью преобразований графиков построить график функции 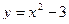 .
.
31. Решить неравенство методом интервалов:
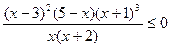 .
.
32. С помощью преобразований графиков построить график функции 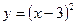 .
.
33. Доказать тождество:
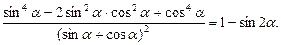
34. Решить неравенство методом интервалов:
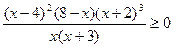 .
.
35. Дано: 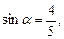
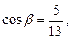
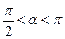 ,
, 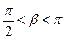 . Найти:
. Найти: 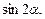
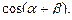
36. Найти комплексно-сопряженное число для числа 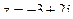 и построить эти числа на комплексной плоскости.
и построить эти числа на комплексной плоскости.
37. Дано: 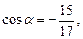
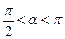 . Найти:
. Найти: 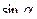 .
.
38. Найти комплексно-сопряженное число для числа 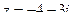 и построить эти числа на комплексной плоскости.
и построить эти числа на комплексной плоскости.
39. Упростить выражение:
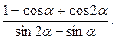
40. Перечислить свойства функции 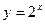 и построить ее график.
и построить ее график.
41. Упростить выражение:
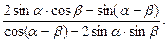
42. Перечислить свойства функции 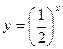 и построить ее график.
и построить ее график.
43. Упростить выражение:
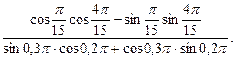
44. Перечислить свойства функции 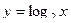 и построить ее график.
и построить ее график.
45. Упростить выражение:
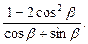
46. Перечислить свойства функции 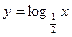 и построить ее график.
и построить ее график.
47. Найти 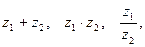 если
если 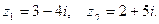
48. Упростить выражение:
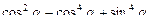
49. Найти числовое значение выражения:
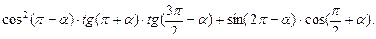
50. Решить квадратное уравнение во множестве комплексных чисел:
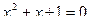 .
.
51. Найти значение выражения:
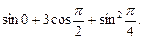
52. Представить в тригонометрической форме комплексное число 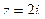
53. Найти 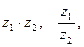 если
если 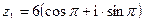 ,
, 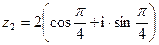 .
.
54. Построить в одной системе координат графики функций 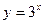 и
и 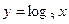 .
.
55. Составить треугольник Паскаля до n=9. Найти разложение выражения (a+b)9.
56. Решить квадратное уравнение во множестве комплексных чисел:
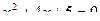 .
.
57. Найти 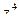 ,
, 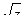 если
если 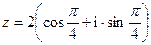 .
.
58. Построить в одной системе координат графики функций 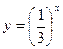 и
и 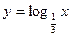 .
.
59. Вычислить:
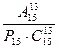 .
.
60. Построить в одной системе координат графики функций 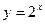 и
и 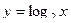 .
.
61. Найти 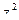 , если
, если 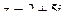 .
.
62. Записать в виде бесконечной периодической дроби следующие числа:
15; 5,03; 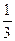 ;
; 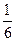 ;
; 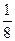 .
.
63. В одной корзине находятся 5 белых и 10 черных шаров. Найти вероятность того, что вынутый наугад шар окажется черным.
64. Построить в одной системе координат графики функций 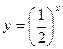 и
и 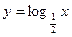 .
.
65. Могут ли синус и косинус одного и того же числа быть равными соответственно:
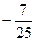 и
и 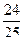 .
.
66. В одной корзине находятся 5 белых и 10 черных шаров. Найти вероятность того, что вынутый наугад шар окажется черным.
67. Могут ли синус и косинус одного и того же числа быть равными соответственно:
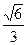 и
и 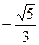 .
.
68. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно:
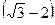 и
и 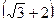 .
.
69. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно:
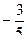 и
и 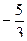 .
.
70. Могут ли тангенс и котангенс одного и того же числа быть равными соответственно:
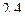 и
и 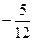 .
.
Часть 2
71. n-й член числовой последовательности выражается формулой 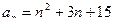 . Найти 3-й член этой последовательности. Являются ли числа 7 и 19 членами этой последовательности, и если являются, то каковы их порядковые номера?
. Найти 3-й член этой последовательности. Являются ли числа 7 и 19 членами этой последовательности, и если являются, то каковы их порядковые номера?
72. Вычислить площадь фигуры, ограниченной линиями 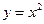 ,
, 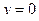 ,
, 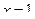 ,
, 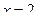 .
.
73. Найти производную функции 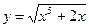 .
.
74. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом 45о, если его проекция – правильный треугольник со стороной а.
75. Точка движется прямолинейно по закону 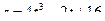 . Вычислить скорость и ускорение точки в момент времени
. Вычислить скорость и ускорение точки в момент времени 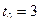 с.
с.
76. Три латунных куба с ребрами 3 см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба?
77. Скорость движения точки изменяется по закону 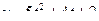 (м/с). Найти путь s, пройденный точкой за 4 с от начала движения.
(м/с). Найти путь s, пройденный точкой за 4 с от начала движения.
78. Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98 см3. Чему равно ребро куба?
79. Составить уравнение касательной к линии 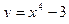 , проходящей через точку А (1; –2).
, проходящей через точку А (1; –2).
80. Концы данного отрезка длиной 125 см отстоят от плоскости на 100 см и 56 см. Найти длину его проекции.
81. Найти производную четвертого порядка следующей функции: 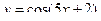 .
.
82. Отрезок длиной 10 см пересекает плоскость, концы его удалены от плоскости на расстояние 5 см и 3 см. Найти длину проекции отрезка на плоскость.
83. Вычислить определенный интеграл 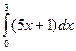 .
.
84. Из некоторой точки, находящейся на расстоянии 6 см от плоскости, проведена к ней наклонная, равная 10 см. Найти ее проекцию на данную плоскость.
85. Исследовать функцию 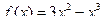 и построить ее график.
и построить ее график.
86. Из некоторой точки проведены к данной плоскости перпендикуляр, длина которого равна а, и наклонная. Угол между ними равен 45о. Найти длину наклонной.
87. Вычислить значение производной следующих функций в точке 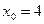 :
:
а) 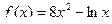 ; б)
; б) 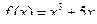 .
.
88. Измерения прямоугольного параллелепипеда 15 м, 50 м и 36 м. Найти ребро равновеликого ему куба.
89. Найти производную функции 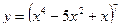 .
.
90. В банку, диаметр основания которой 18 см, опущен камень, вследствие чего уровень воды в банке поднялся на 3 см. Найти объем камня.
91. Найти производную функции 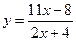 .
.
92. В правильной усеченной четырехугольной пирамиде стороны верхнего и нижнего оснований равны 6 и 10 см, двугранный угол при ребре нижнего основания равен 450. Найти объем этой пирамиды.
93. Найти производную функции 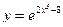 .
.
94. В правильной усеченной четырехугольной пирамиде стороны верхнего и нижнего оснований равны 6 и 10 см, двугранный угол при ребре нижнего основания равен 450. Найти площадь боковой и полной поверхности.
95. Найти производную функции 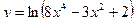 .
.
96. Диаметры оснований усеченного конуса равны 6 и 10 см, его образующая наклонена к плоскости основания под углом 450. Найти объем этого конуса.
97. Найти неопределенный интеграл 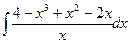 .
.
98. Диаметры оснований усеченного конуса равны 6 и 10 см, его образующая наклонена к плоскости основания под углом 450. Найти площадь боковой и полной поверхности.
99. Решить тригонометрическое уравнение:
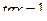 .
.
100. Сфера задана уравнением: 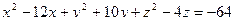 .
.
Привести уравнение сферы к общему виду и найти объем шара, ограниченного этой сферой.
101. Найти производную функции 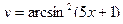 .
.
102. Сфера задана уравнением: 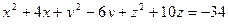 .
.
Привести уравнение сферы к общему виду и найти объем шара, ограниченного этой сферой.
103. На отрезке [–10; 10] найти наибольшее и наименьшее значение функции 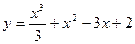 .
.
104. Сфера задана уравнением: 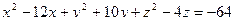 .
.
Привести уравнение сферы к общему виду и найти площадь этой сферы.
105. Найти производную функции 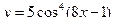 .
.
106. Сфера задана уравнением: 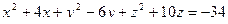 .
.
Привести уравнение сферы к общему виду и найти площадь этой сферы.
107. Найти промежутки монотонности функции 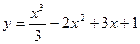 .
.
108. В правильной четырехугольной призме сторона основания 4 м, боковое ребро 7 м. Найти боковую и полную поверхности призмы.
109. Вычислить определенный интеграл 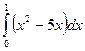 .
.
110. В правильной четырехугольной пирамиде сторона основания 5 м, апофема 6 м. Найти боковую и полную поверхности пирамиды.
111. Найти неопределенный интеграл  .
.
112. Осевое сечение конуса – равнобедренный треугольник с основанием 8 см и боковой стороной 5 см. Найти объем конуса.
113. Найти точки экстремума и экстремумы функции 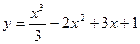 .
.
114. Площадь осевого сечения цилиндра равна 24 см2, высота цилиндра равна 6 см. Найти объем цилиндра.
115. Вычислить площадь фигуры, ограниченной линиями 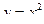 ,
, 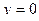 ,
, 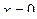 ,
, 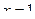 .
.
116. Измерения прямоугольного параллелепипеда 2, 3 и 6 см. Найти радиус описанного около него шара.
117. Найти производную функции 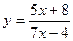 .
.
118. Радиусы оснований усеченного конуса равны 4 и 1 см, образующая 5 см. Найти его высоту.
119. Найти производную функции 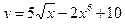 .
.
120. Радиус основания конуса 3 м, высота 4 м. Найти образующую и площадь осевого сечения.
121. Решить тригонометрическое уравнение:
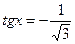 .
.
122. Радиус основания цилиндра 4 м, высота 6 м. Найти диагональ осевого сечения.
123. Вычислить определенный интеграл 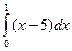 .
.
124. Построить сечение куба ABCDA1 B1 C1 D1 плоскостью, проходящей через диагональ AD1 грани AA1 D1 D и середину M ребра BB1.
125. Решить тригонометрическое уравнение:
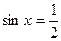 .
.
126. Высота правильной четырехугольной пирамиды равна 7 м, а сторона основания равна 8 м. Найти боковое ребро и боковую поверхность.
127. Решить тригонометрическое уравнение:
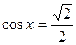 .
.
128. Измерения прямоугольного параллелепипеда равны 6, 4 и 12 м. Найти диагональ параллелепипеда.
129. Вычислить определенный интеграл 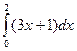 .
.
130. В правильной четырехугольной призме площадь основания равна 144 см2, а высота равна 14 см. Найти диагональ этой призмы.
131. Решить тригонометрическое уравнение:
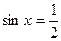 .
.
132. Двугранный угол равен 45о. На одной грани дана точка на расстоянии а от другой грани. Найти расстояние от этой точки до ребра.
133. Решить тригонометрическое уравнение:
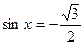 .
.
134. При каких m и n векторы 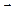 (6; –18; n) и
(6; –18; n) и 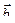 (5; m; 10) коллинеарны?
(5; m; 10) коллинеарны?
135. Решить тригонометрическое уравнение:
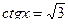 .
.
136. Известно, что 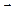 (9; –2; 1) и
(9; –2; 1) и 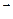 (4; 3; 0).
(4; 3; 0).
Найти: 1) 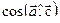 ;
;
2) 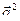 ;
;
3) координаты векторов 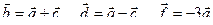 .
.
137. Решить тригонометрическое уравнение:
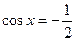 .
.
138. Измерения прямоугольного параллелепипеда 2, 3 и 6 см. Найдите радиус описанного около него шара.
139. Найти неопределенный интеграл 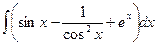 .
.
140. Двугранный угол равен 30о. На одной грани дана точка на расстоянии а от другой грани. Найти расстояние от этой точки до ребра.
141. Вычислить определенный интеграл 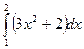 .
.
142. При каких m и n векторы 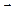 (12; –6; n) и
(12; –6; n) и 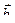 (6; m; 5) коллинеарны?
(6; m; 5) коллинеарны?
143. Двугранный угол равен 60о. На одной грани дана точка на расстоянии а от другой грани. Найти расстояние от этой точки до ребра.
144. Найти производную функции 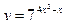 .
.
145. При каких m и n векторы 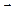 (4; –10; n) и
(4; –10; n) и 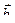 (2; m; 6) коллинеарны?
(2; m; 6) коллинеарны?
Перечень рекомендуемых учебных изданий,
Специальность
11.02.16 Монтаж, техническое обслуживание и ремонт
электронных приборов и устройств
Квалификация выпускника
специалист по электронным приборам и устройствам
Специальность
15.02.15 Технология металлообрабатывающего производства
Квалификация выпускника
техник
| Разработчик: Леонтьева Т.Ю., преподаватель |
2018
Фонд оценочных средств (далее – ФОС) по учебной дисциплине (далее – УД) ПД.01. Математика: алгебра, начала математического анализа, геометрия программы подготовки специалистов среднего звена (ППССЗ) по специальностям 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств и 15.02.15 Технология металлообрабатывающего производства базового уровня разработан на основе Федерального государственного образовательного стандарта (далее – ФГОС) по специальностям 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств и 15.02.15 Технология металлообрабатывающего производства в соответствии с рабочей программой учебной дисциплины ПД.01. Математика: алгебра, начала математического анализа, геометрия.
Разработчик (и):
МЦК "ЧЭМК"______ преподаватель__ Т.Ю. Леонтьева
(место работы) (занимаемая должность) (инициалы, фамилия)
__________________ ______________ ____________
(место работы) (занимаемая должность) (инициалы, фамилия)
СОГЛАСОВАНО
Председатель ЦК ________ ______________ ______________
(название ЦК) (подпись) (расшифровка подписи)
Содержание
- Область применения ФОС по учебной дисциплине ПД.01. Математика: алгебра, начала математического анализа, геометрия
- Программа текущего контроля успеваемости студентов
- ФОС для проведения текущего контроля
- Программа промежуточной аттестации студентов
- ФОС для промежуточной аттестации
1. Программа текущего контроля успеваемости студентов
по учебной дисциплине ПД.01. Математика: алгебра, начала математического анализа, геометрия
ФОС предназначен для проверки результатов освоения учебной дисциплины основной профессиональной образовательной программы (далее ОПОП) по специальностям 11.02.16 Монтаж, техническое обслуживание и ремонт электронных приборов и устройств и 15.02.15 Технология металлообрабатывающего производства.
Текущий контроль освоения студентами материала учебной дисциплины Математика: алгебра и начала математического анализа, геометрия состоит из следующих видов: оперативный и рубежный контроль.
При проведении текущего контроля используются следующие формы (в скобках указан порядковый номер оценочного средства в структуре ФОС):
- аудиторная контрольная работа (3, 5, 7, 8, 10, 13, 15, 17, 19, 22);
- проверочная работа (2, 11, 14, 16);
- письменное тестирование (6, 12);
- индивидуальный опрос (1, 4, 9, 18, 20, 21, 23);
При проведении аудиторной контрольной работы студент прочитывает задания соответствующего варианта контрольной работы и отвечает письменно на вопросы (решает задания) в любом порядке. Время выполнения контрольной работы: 45 мин.
Проверочная работа в отличие от контрольной работы характеризуется меньшим охватом проверяемых тем (разделов) и меньшим временем, отведенным на ее выполнение в рамках аудиторного занятия (20-25 мин.).
При проведении письменного тестирования студенты должны внимательно прочитать задания теста и выбрать правильные ответы из предложенных вариантов. Если в тесте приведены задачи, то для выбора верного ответа студенту необходимо их решить. Количество правильных ответов и максимальное время прохождения теста указывается в задании в зависимости от темы и количества вопросов в тесте.
Индивидуальный опрос имеет своей целью основную проверку знаний и умений отдельных студентов. Студенты вызываются, как правило, к доске, хотя возможны ответы и с места, если не требуется записи, за которой должна следить группа, или использовать наглядные пособия и ТСО. При подготовке к индивидуальному опросу по предложенным преподавателем темам студентам необходимо руководствоваться рекомендациями к подготовке устного сообщения. В содержание ответа может включаться объяснение теоретического материала, выполнение практических заданий. При индивидуальном опросе обращается внимание на обстоятельный и осознанный ответ студента, логичность его суждений, доказательность выдвигаемых положений, умение практически применять усвоенные знания. Чрезвычайно важно привлечь внимание всех студентов группы к ответу товарища, обеспечить их активное участие в этой части урока, которая отведена опросу. Достигается это таким приемами, как постановка вопроса (или задания) всей группе, а затем вызов для ответа намеченного студента, привлечение всех студентов к комментированию отдельных положений, оригинальных способов выполнения упражнений и т.д. практически, таким образом, индивидуальный опрос сочетается с фронтальным.
Критерии оценки уровня освоения
При проведении текущего контроля успеваемости студентов по учебной дисциплине ПД.01. Математика: алгебра и начала математического анализа, геометрия используются следующие критерии оценок:
1) Критерии оценки выполнения аудиторной контрольной работы, проверочной работы, письменного теста:
| Процент результативности (правильные ответы, %) | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | |
| 90 ÷ 100 | 5 | отлично |
| 80 ÷ 89 | 4 | хорошо |
| 70 ÷ 79 | 3 | удовлетворительно |
| менее 70 | 2 | неудовлетворительно |
Все запланированные контрольные, проверочные работы и тесты по дисциплине обязательны для выполнения. Студент, представивший работу, которая была оценена на «неудовлетворительно», не допускается к сдаче экзамена по дисциплине.
2) Критерии оценки индивидуального опроса:
оценка устного сообщения проводится по следующим критериям:
- содержательный (знание предмета и свободное владение материалом, грамотное использование научной терминологии, импровизация, речевой этикет): 0-30 баллов,
- логический (стройное логико-композиционное построение речи, доказательность, аргументированность): 0-30 баллов,
- речевой (использование языковых (метафоры, фразеологизмы, пословицы, поговорки и т.д.) и неязыковых (поза, манеры и т.д.) средств выразительности; фонетическая организация речи, правильность ударения, четкая дикция, логические ударения и т.д.): 0-20 баллов,
- психологический (взаимодействие с аудиторией (прямая и обратная связь), знание и учет законов восприятия речи, использование различных приемов привлечения и активизации внимания): 0-20 баллов.
| Количество набранных баллов по критериям оценки устного сообщения | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | |
| 90 ÷ 100 | 5 | отлично |
| 80 ÷ 89 | 4 | хорошо |
| 70 ÷ 79 | 3 | удовлетворительно |
| менее 70 | 2 | неудовлетворительно |
Для оценки уровня освоения дисциплин, профессиональных модулей (их составляющих) в колледже устанавливаются следующее соответствие:
«отлично» - высокий уровень освоения;
«хорошо», «удовлетворительно» - достаточный уровень освоения;
«неудовлетворительно» - низкий уровень освоения.
Дата: 2019-03-05, просмотров: 1588.