Составим алгоритм графического метода решения задач линейных оптимизационных задач:
Этап 1. Строим прямые линии, уравнения которых получаем заменой в ограничениях-неравенствах знаков неравенств на знаки равенств.
Этап 2. Определяем полуплоскости, соответствующие заданным ограничениям.
Этап 3. Находим многогранник области допустимых решений как область, где пересекаются все полу плоскости.
Примечание. Если такая область не существует, значит данная система ограничений несовместима и задача не имеет решений.
Этап 4. Строим вектор нормали 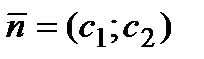 , задающий направление роста значений целевой функции.
, задающий направление роста значений целевой функции.
Этап 5. Строим линию уровня – прямую 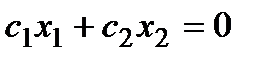 (т.е.
(т.е. 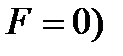 , перпендикулярной (под прямым углом) к вектору
, перпендикулярной (под прямым углом) к вектору 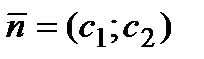 и проходящей через начало координат.
и проходящей через начало координат.
Этап 6. Перемещаем линию уровня в направлении вектора 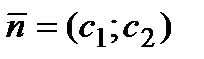 для задачи максимизации целевой функции или в противоположном направлении для задачи минимизации. Последняя вершина многогранник области допустимых решений через которую пройдет линия уровня и будет точкой, в которой целевая функция достигает экстремального значения.
для задачи максимизации целевой функции или в противоположном направлении для задачи минимизации. Последняя вершина многогранник области допустимых решений через которую пройдет линия уровня и будет точкой, в которой целевая функция достигает экстремального значения.
Примечание 1. В случае поиска максимума, если область допустимых решений не является замкнутым пространством точек в направлении вектора 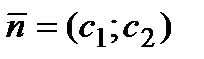 значение целевой функции будет равно бесконечности.
значение целевой функции будет равно бесконечности.
Примечание 2. В случае поиска минимума, если область допустимых решений не является замкнутым пространством точек в направлении противоположному вектору 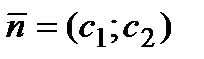 значение целевой функции будет равно минус бесконечности.
значение целевой функции будет равно минус бесконечности.
Этап 7. Определяем координаты вершины многогранника области допустимых решений, определенной на предыдущем этапе, путем решения системы уравнений, на пересечении которых она находится.
Этап 8. Вычисляем экстремальное значение целевой функции в оптимальной точке.
2. Построение выпуклого многоугольника возможных решений и определение оптимального плана с помощью градиента функции цели.
Если задача линейного программирования в стандартной форме содержит всего лишь две переменные x 1 и x 2 (т.е. n=2), то ее можно решить следующим способом, основанным на ее геометрической интерпретации.
Каждое неравенство системы ограничений и условие неотрицательности представляют собой полуплоскость. Пересечение полуплоскостей образует выпуклое многоугольное множество (многогранник допустимых решений).
Целевая функция графически изображается множеством параллельных прямых, называемых линиями уровня, каждой из которых соответствует конкретное значение z.
Для решения задачи линия уровня сдвигается в пределах области допустимых решений (многогранника допустимых решений) в направлении вектора-градиента 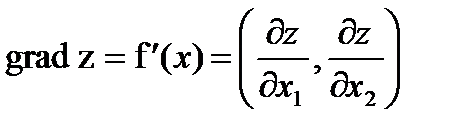 до самой крайней точки области для задачи максимизации, и в направлении антиградиента
до самой крайней точки области для задачи максимизации, и в направлении антиградиента 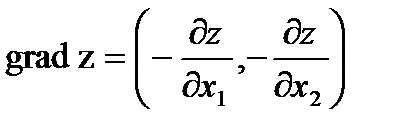 для задачи минимизации. Координаты этой точки и определяют решение ЗЛП (оптимальный план задачи).
для задачи минимизации. Координаты этой точки и определяют решение ЗЛП (оптимальный план задачи).
Пример. Студент имеет 10 часов дневного времени, которое он должен распределить на учебу и развлечения. Развлечения привлекательнее в два раза. Однако для того, чтобы успешно учиться, на развлечения нельзя тратить более 4 часов дневного времени. Как распределить дневное время, чтобы получить максимальное удовольствие от работы и отдыха.
Решение. Составим экономико-математическую модель для данной задачи. Пусть х1 – количество времени, потраченное на работу, х2 – количество времени, потраченное на игры.
Тогда целевая функция имеет вид:
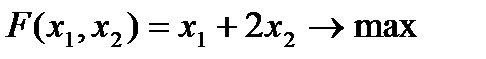
и условия-ограничения можно записать следующим образом:
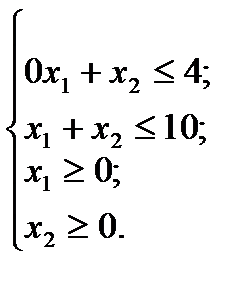
допустимых решений задачи. Для этого в неравенствах системы ограничений знаки неравенств заменим на знаки точных равенств:
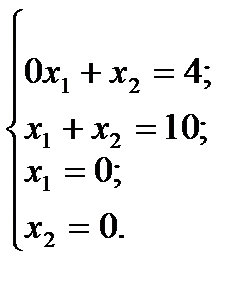
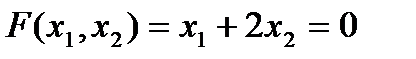
Построив полученные граничные прямые, найдем соответствующие полуплоскости допустимых значений переменных и их пересечение (рис. 4).
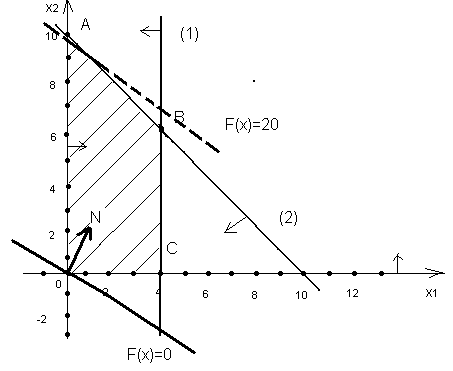
Рис. 4. Полуплоскости допустимых значений переменных.
Направление стрелок от каждой граничной прямой определяется путем непосредственной подстановки в неравенство координат произвольно взятой точки, например (0,0), и при удовлетворении данного неравенства направляем стрелки в сторону контрольной точки, в противном случае – наоборот. Полученное пространство решений есть многоугольник АВСD.
Угловые точки многоугольника решений имеют следующие координаты: А(0;10), B(4;6), C(4;0), D(0;0).
Для нахождения максимума целевой функции строим начальную прямую и вектор-градиент N(1;2). Координатами вектора N являются коэффициенты целевой функции при переменных х1 и х2. Для построения графика целевой функции задаем произвольное значение F(X). Если F(X)=0, то прямая проходит через начало координат.
Вектор-градиент показывает направление возрастания целевой функции. Передвигая начальную прямую параллельно самой себе в направлении вектора-градиента N, находим точку максимума целевой функции. Она будет в точке А(0;10), и максимальное значение 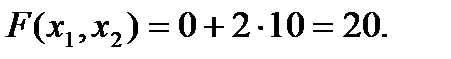
Таким образом, студент тратит 0 часов дневного времени на работу и 10 часов на игры, получая максимальное удовольствие в 20 единиц.
Лекция № 9
Тема: Симплексный метод для задач с естественным базисом
План:
Дата: 2019-02-19, просмотров: 529.