| № п/п | Тема | Наименование практического занятия |
| 1 | Тема 1.2. Системы единиц | Единицы измерения физических величин. |
| 2 | Тема 2.1. Техника измерений | Виды и методы измерений. |
| 3 | Тема 2.2. Измерения. Погрешности. Эталон. | Погрешности измерений, испытаний и контроля. Основные характеристики измерительных приборов. |
| 4 | Обнаружение грубых погрешностей "Метод трех сигм" | |
| 5 | Тема 3.2. Обеспечение качетсва | Расчет надежности в технике |
| 6 | Определение качества продукции или услуги методом попарного сравнения | |
| 7 | Тема 4.2. Категории и виды стандартов | Анализ маркировочных знаков на продукцию. Анализ реальных штрихкодов. Проверка их подленности. |
| 8 | Тема 5.1Сертификация | Заполнение декларации качества и сертификатов соответствия |
Практическая работа №1
ЕДИНИЦЫ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН
Цель работы. Освоить перевод основных и производных единиц в кратные, дольные единицы и наоборот.
|
|
Порядок выполнения работы : Для выполнения работы необходимо получить у преподавателя задание и перевести заданные единицы в требуемые. Результаты записать в таблицу
Краткие теоретические сведения
Кратные и дольные единицы. Использование целых единиц не всегда удобно, так как в результате измерений получаются либо большие, либо малые их значения. Поэтому в системе СИ введены их десятичные кратные и дольные единицы, которые образуются с помощью множителей. Кратные и дольные единицы величин пишутся слитно с наименованием основной или производной единицы, например микроампер — мкА, гигагерц — ГГц, нанофарад — нФ.
Наиболее удачным способом образования кратных и дольных единиц является принятая в метрической системе мер десятичная кратность между ббльшими и меньшими единицами СИ, которые образуются в результате присоединения приставок, взятых из латинского, греческого и датского языков.
Кратная единица физической величины — это единица, больше системной в целое число раз, например килограмм (103).
Дольная единица физической величины — это единица, меньше системной в целое число раз, например миллисекунда (1(H).
В таблице приведены используемые в электронике множители и приставки.
Сокращенные обозначения единиц (как международных, так и русских), названных в честь ученых и изобретателей, пишутся с заглавных букв, например ватт — Вт, генри — Гн, вольт — В, а единицы, не связанные с чьим-либо именем, пишутся с маленькой буквы, например секунда — с, радиан — рад.
Чтобы не было разночтения в обозначении приставок, начинающихся с одинаковой буквы, например мили и мега, гига и гекто, приставки мега, гига, тера пишутся с заглавной буквы.
Множители и приставки для образования десятичных
кратных и дольных единиц
| Дольные и кратные приставки | Обозначение | ||
| русское | международное | Множитель | |
| пико | п | P | 10-12 |
| нано | н | п | 10-9 |
| микро | мк | М | 10-6 |
| мили | м | m | 10-3 |
| санти | с | s | 10-2 |
| деци | д | d | 10-1 |
| кило | к | k | 103 |
| мега | М | М | 106 |
| гига | Г | G | 109 |
| тера | Т | Т | 1012 |
| Таблица Задание
|
Следует отметить, что десятичность метрической системы СИ является важным ее преимуществом. В приложении 10 приведена таблица единиц физических величин, используемых в электронике и вычислительной технике.
Содержание отчета.
1. Наименование и цель работы.
2. Таблица
3. Ответы на контрольные вопросы.
Контрольные вопросы
1. Какая метрическая система единиц измерения используется в настоящее время в большинстве стран мира?
2. Укажите достоинства используемой в России метрической системы единиц физических величин.
3. Что такое единица физической величины?
4. Перечислите основные единицы системы СИ.
5. Назовите производные единицы системы СИ.
6. Какие дополнительные единицы включены в систему СИ? Сколько их?
7. Какой способ образования кратных и дольных единиц принят в используемой в России метрической системе единиц?
8. Наименования каких единиц пишутся с заглавной буквы?
9. Наименования каких единиц пишутся с маленькой буквы?
10. Наименование каких приставок пишется с заглавной буквы и почему?
11. Наименование каких приставок пишется с маленькой буквы?
12. Какую степень (положительную или отрицательную) имеют кратные единицы?
13. Какую степень (положительную или отрицательную) имеют дольные единицы?
14. Что такое система физических величин?
Практическая работа №2
ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
Цель работы: 1. Формировать знания студентов по теме, добиться понимания вопросов, обеспечивать усвоение и закрепление в ходе занятия основных понятий темы. Применять знания в решении новых познавательных и практических задач.
Порядок выполнения работы:
- Опрос студентов:
Виды измерения:
- Прямые
- Косвенные
- Совокупные
- Совместные
Методы измерения:
- Метод непосредственной оценки
- Метод сравнения с мерой
- Нулевой метод
- Дифференциальный метод
- Метод замещения.
Информирование:
Когда наш предок — древний, но уже мыслящий человек попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего жилища с собственным ростом. А ведь это и есть измерение — сравнение неизвестной величины с однородной ей величиной, принятой за единицу.
В наши дни этот познавательный процесс не обходится без измерительных средств — приборов и мер. Нет ни одной области практической деятельности человека, где можно было обойтись без измерений:
•ребенок появляется на свет, еще не имеет имени, но нам становятся известны его рост, вес, температура — уже в первые минуты жизни нам приходится сталкиваться с линейкой, весами, термометром.
•каждое утро, выходя из дома, мы оцениваем температуру воздуха на улице, и одеваем при необходимости легкую или теплую одежду.
Итак, измерение ФВ — это нахождение физической величины опытным путём с помощью специальных технических средств.
Виды измерений
Виды измерений определяются:
• физическим характером измеряемой величины,
• требуемой точностью измерения,
• необходимой скоростью измерения,
• условиями и режимом измерений и т.д.
В метрологии существует множество видов измерений, и число их постоянно увеличивается.
1) По способу получения информации:
• Прямые измерения — это нахождение искомого значения величины из опытных данных путем экспериментального сравнения.
*длину измеряют непосредственно линейкой, температуру — термометром, силу — динамометром.
• Косвенные измерения — используют результаты прямых измерений величин, связанных с искомой определенной зависимостью.
*электрическое сопротивление находят путем деления падения напряжения на величину силы электрического тока R=U/I.
• Совокупные измерения — связаны с решением системы уравнений, составляемых по результатам одновременных измерений нескольких однородных величин. Решение системы уравнений дает возможность вычислить искомую величину. Однородные — значит подобные, например, длина и диаметр.
* при определении взаимоиндуктивности катушек М используют два метода: сложения и вычитания полей. Еслииндуктивность одной из них L1, а другой - L2 , то находят:
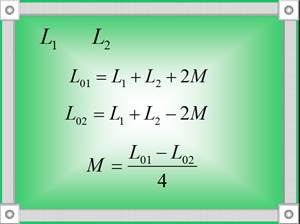
• Совместные измерения — это измерения двух или более неоднородных физических величин для определения зависимости между ними.
*измерение сопротивления проводника при фиксированной температуре t:

2 По характеру изменения измеряемой величины в процессе измерений:
• Статистические измерения связаны с определением характеристик случайных процессов. *определение звуковых сигналов, уровня шумов и т.д.
• Статические измерения — когда измеряемая величина практически постоянна.
• Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения.
3) По количеству измерительной информации:
• Однократные измерения — это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.
• Многократные измерения когда число измерений больше количества измеряемых величин. Обычно минимальное число измерений в данном случае больше трех. Преимущество многократных измерений — в значительном снижении влияний случайных факторов на погрешность измерения.
4) По отношению к основным единицам измерения:
• Абсолютными измерениями называют такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа.
* в формуле Эйнштейна масса (m) — основная ФВ, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) — физическая константа.
• Относительные измерения базируются на установлении отношения измеряемой величины к однородной, применяемой в качестве единицы.
Методы измерений
Приведенные виды измерений включают различные методы, т.е. способы решения измерительной задачи с теоретическим обоснованием и разработкой использования СИ.
Метод измерений — это теоретическое обоснование принципов измерения и разработка способов применения средств измерения.
Как известно, искомое значение ФВ находится посредством сопоставления ее с мерой, материализующей единицу этой величины. В зависимости от способа применения меры различают:
•методы непосредственной оценки
•методы сравнения.
1. Метод непосредственной оценки — значение ФВ непосредственно определяют по отсчётному устройству прямого действия, т.е. такого прибора, который реагирует непосредственно на всю измеряемую величину или производимый ею эффект. Этот метод прост, но не обеспечивает высокой точности.
*измерение давления — манометром, массы — на весах, силы электрического тока — амперметром.
2. Метод сравнения с мерой — измеряемую величину сравнивают с величиной, воспроизводимой мерой.
*измерение сопротивления по мостовой схеме или измерение массы на равноплечих весах.
Отличительной чертой методов сравнения является непосредственное участие меры в процедуре измерения, в то время как в методе непосредственной оценки мера в явном виде при измерении не присутствует, а ее размеры перенесены на отсчетное устройство (шкалу) СИ заранее, при его градуировке. Обязательным в методе сравнения является наличие сравнивающего устройства.
 Метод сравнения с мерой имеет несколько разновидностей:
Метод сравнения с мерой имеет несколько разновидностей:
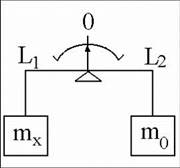
• Нулевой метод (или метод полного уравновешивания) — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и встречного воздействия меры на сравнивающее устройство сводят к нулю.
*Измерение массы на равноплечих весах, когда воздействие на весы массы полностью уравновешивается массой гирь.
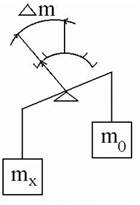
•При дифференциальном методе полное уравновешивание не производят, а разность между измеряемой величиной и величиной, воспроизводимой мерой отсчитывается по шкале прибора.
*Измерение массы на равноплечих весах, когда воздействие массы на весы частично уравновешивается массой гирь, а разность масс отсчитывается по шкале весов, градуированной в единицах массы.
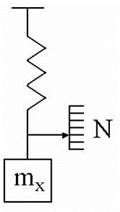
• Метод замещения — метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой.
*Взвешивание на пружинных весах. Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу замещают массой гирь , подбирая ее так, чтобы указатель весов установился точно в том же положении, что и в первом случае.
Задачи:
- Отрезок проволоки длиной l=1 м и диаметром d = 0,1 м имеет электрическое сопротивление R = 51 Ом. Из какого материала изготовлена проволока?
- Для идентификации материала, из которого сделан цилиндр, штангенциркулем измерили его диаметр d= 1 см и высоту h=5 см. Из какого материала сделан цилиндр, если его масса, определенная взвешиванием, оказалась равной m=0,0349 кг.
- Для определения взаимоиндуктивности двух катушек была измерена индуктивность при согласном Lc = 25мГн и встречном Lв = 1мГн включении катушек. Чему равна взаимоиндуктивности между катушками и к какому виду относятся эти измерения?
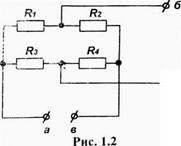
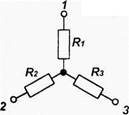
Для определения сопротивления резисторов
тензорезисторного моста микроэлектронного
датчика давлений были измерены сопротивления
между его зажимами
Rаб = Rбв = Rвг = Rга = 120 Ом. (Рис.1.2.)
Чему равны сопротивления резисторов R1,R2,R3,R4 и к
Какому виду относятся эти измерения?
 5.
5.
Для определения сопротивлений обмоток электродвигателя, включенных звездой (рис. 2), были измерены сопротивления между зажимами обмоток R12 = R23 = R31 = 10 Ом.
Чему равны сопротивления обмоток R1, R2, R3 и к какому виду относятся эти измерения?
- При нагревании сопротивление резистора, выполненного из платины, определяется соотношением RΘ = R0(1+AΘ+BΘ2), где R0 - сопротивление, при 0 0С, А и В – постоянные коэффициенты. Для их определения было измерено сопротивление резистора при температуре: RΘ1= 100 Ом при Θ1=0 0С, RΘ2= 139,657 Ом при Θ2=100 0С и RΘ3 = 222,441 Ом при Θ3=300 0С. Определите параметры резистора R0, А и В. К какому виду относятся эти измерения?
- При нагревании сопротивление металлического резистора определяется соотношением RΘ = R0(1+ αΘ), где R0 – сопротивление при температуре 0 0С, α – температурный коэффициент сопротивления. Сопротивление резистора было измерено при двух температурах: Θ1= 20 0С, Θ2=100 0С, - и получены значения сопротивлений резистора RΘ1= 54,281 Ом, RΘ2= 71,4 Ом. Определить параметры резистора R0 и α и указать, к какому виду относятся эти измерения.
- При нагревании сопротивление термистора изменяется по закону R = АеВ/Т, где А и В – постоянные коэффициенты, Т – абсолютная температура, К. Было измерено сопротивление термистора: при температуре Θ1= 20 0С, R1= 5 кОм и при температуре Θ2= 60 0С, R2= 0,676 кОм. Определить параметры термистора А и В. К какому виду относятся эти измерения?
- Решить задачу, аналогичную задаче 8, при значениях: Θ1= 20 0С, R1= 100кОм, Θ2= 100 0С, R2= 11,2 Ом.
- Решить задачу, аналогичную задаче 8, при значениях: Θ1= 20 0С, R1= 50кОм, Θ2= 150 0С, R2= 92 кОм.
 11.
11.
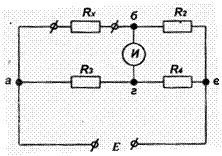
8. В схеме, показанной на рисунке, используется нулевой метод измерений. При каком значении
Сопротивления резистора Rх схема будет
уравновешена, если R2=R3=100 Ом, R4= 1000 Ом,
Е= 10 В, входное сопротивление индикатора Rи можно
считать бесконечно большим.
- С помощью равноплечих рычажных весов и набора гирь
1, 3, 5, 10 и 30г производилось взвешивание предметов,
имеющих следующие значения массы: m1 = 16г, m2 =17г, m3 =27г,
m4 = 32г, m5 =39г, m6=47г. Каким образом можно уравновесить
весы, используя минимальное количество гирь? 

Практическая работа №3
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ, ИСПЫТАНИЙ И КОНТРОЛЯ. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
 Цель работы: 1. Формировать знания студентов по теме, добиться понимания вопросов, обеспечивать усвоение и закрепление в ходе занятия основных понятий темы. Применять знания в решении новых познавательных и практических задач.
Цель работы: 1. Формировать знания студентов по теме, добиться понимания вопросов, обеспечивать усвоение и закрепление в ходе занятия основных понятий темы. Применять знания в решении новых познавательных и практических задач.
Порядок выполнения работы:
1. Опрос студентов;
2. Информирование;
3. Решение задач;
4. Проверка решения задач;
5. Защита практической работы.
 Информирование:
Информирование:
Погрешность средств измерения - это разность между показанием средства измерений и истинным (действительным) значением измеряемой величины.
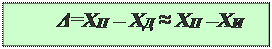 Абсолютная погрешность (Δ) средств измерений – это погрешность, выраженная в единицах измеряемой величины
Абсолютная погрешность (Δ) средств измерений – это погрешность, выраженная в единицах измеряемой величины
Относительная погрешность ( δ ) средства измерений – это отношение абсолютной погрешности средства измерений к результату измерений или к действительному значению измеряемой величины.
|
Где Хп – показание прибора, ХД – действительное значение измеряемой величины.
Обычно относительная погрешность выражается в процентах
|
Приведённая погрешность средств измерений – это отношение абсолютной погрешности средства измерений к нормирующему значению. Нормирующее значение ХN – это условно принятое значение, равное верхнему пределу измерений, диапазону измерения.

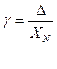
Метрологические характеристики – характеристики средств измерения, оказывающие влияние на результаты измерений.
На практике наиболее распространены следующие метрологические характеристики СИ.
Диапазон измерений – область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ.
Предел измерения – наибольшее или наименьшее значение диапазона измерения.
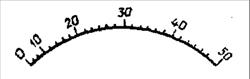
*у шкалы на рисунке начальный участок (~20%) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10...50 ед. (там где одинакова цена деления.
Цена деления шкалы – определяется по формуле:

где: Х – конечное значение шкалы на данном пределе измерения, например, 200 В,
N – число отметок (рисок) всей шкалы, например, 20.
Получается, что в данном случае цена деления равна 10 В/дел. Тогда если стрелка остановится на пяти делениях, то общее показание будет равно 50 В.
Таким образом, цена деления – это расстояние между двумя соседними отметкам шкалы.
Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной - переменную. В этом случае нормируется минимальная цена деления.
Цена деления шкалы – это разность значений величины, соответствующих двум соседним отметкам шкалы средства измерений.
Чувствительность прибора – численно равна перемещению указателя, соответствующему единице измеряемой величины.

* например, чувствительность амперметра к току равна 20 делений на А.
Чувствительность нельзя отождествлять с порогом чувствителъности – наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.
Постоянная прибора – величина, обратная чувствительности. Численно равна измеряемой величине, соответствующей перемещению указателя на одно деление шкалы прибора.

Функции СИ:
·воспроизводят величину заданного размера;
*гиря - заданную массу, магазин сопротивлений - ряд дискретных значений сопротивления;
·вырабатывают сигнал (показание), несущий информацию о значении измеряемой величины.
Показания СИ либо непосредственно воспринимаются органами чувств человека (например, показания стрелочного или цифрового приборов), либо они недоступны восприятию человеком и используются для преобразования другими СИ.
Класс точности – это обобщенная характеристика данного средства измерений, отражающая уровень их точности, выражаемая пределами допустимых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
Для приборов с чисто аддитивной полосой погрешностей нормируется предельное значение основной приведенной погрешности:
, где ХN – нормирующее значение.
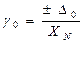
|
Это значение γ0, выраженное в процентах, используется для указания класса точности таких приборов. Предельное значение относительной погрешности определяется:

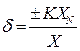
где Х – значение измеряемой величины, ХN- нормирующее значение, К – класс точности.
Узнаем больше об 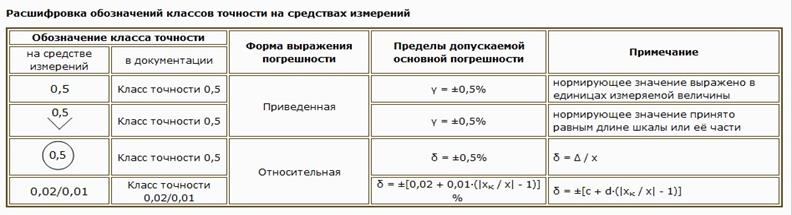 обозначениях Классов точности на СИ
обозначениях Классов точности на СИ
Абсолютная погрешность меры – это разность между номинальным значением меры (указанным в её паспорте) и истинным (действительным) значением воспроизводимой ею величины, приписанное ей на основании калибровки или поверки.
Пределом (максимальным значением) допускаемой погрешности средств измерений называется наибольшая (без учёта знака) погрешность средств измерений, устанавливаемая нормативным документом для данного типа средств измерений, при которой они могут быть допущены к применению. При записи этой погрешности и результата измерения пределу допускаемой погрешности присваиваются знаки ²±². Например,
Dmax = ± 0,15 В, U = (111,45 ± 0,15) В.
Разделение погрешностей по их зависимости от значений X измеряемой или преобразуемой величины является весьма важным, так как изменение 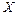 является одной из причин появления погрешностей.
является одной из причин появления погрешностей.
Если абсолютная погрешность средства измерений во всем диапазоне измерений ограничена постоянным (не зависящим от текущего значения X) пределом ± D0, то такая погрешность называется аддитивной, т.е. получаемой путем сложения, или погрешностью нуля.
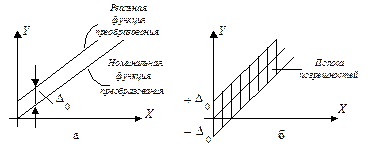 |
Это понятие одинаково применимо как к систематическим (рис.1.15, а), так и случайным (рис.1.15, б) погрешностям.
Рис.1.15
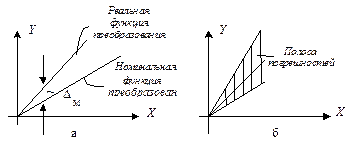 |
Если абсолютная погрешность оказывается пропорциональной текущему значению измеряемой или преобразуемой величины X и возрастает пропорционально росту входной величины, а при Х = 0 она также равна нулю, то такая погрешность называется мультипликативной, т.е. получаемой путём умножения, или погрешностью чувствительности (Dм). Мультипликативная погрешность также может иметь систематический (рис.а) или случайной (рис.б) характер.
.
Для приборов с одновременным присутствием аддитивной и мультипликативной погрешностей предельное значение относительной погрешности определяется по формуле
| δ = ±[с+d( XN ⁄X-1)] |
Где ХN – верхний предел измерения: 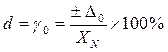 - приведённая погрешность нуля (в начале диапазона); c = γ0 + δs – приведённая погрешность в конце диапазона; δs- относительная мультипликативная погрешность.
- приведённая погрешность нуля (в начале диапазона); c = γ0 + δs – приведённая погрешность в конце диапазона; δs- относительная мультипликативная погрешность.
Класс точности таких приборов указывается в виде дроби c/d, где через косую черту указываются в % приведённые погрешности в конце (с) и начале (d) диапазона.
Задачи:
I. При поверке амперметра с верхним пределом измерения Iв в точке шкалы I получены следующие показания эталонного прибора: Iд Определить абсолютные, относительные и приведенные погрешности в каждой из указанных точек шкалы амперметра. К какому классу точности можно отнести амперметр по результатам поверки?
II. Магнитоэлектрический прибор имеет чувствительность к току SI = Х дел/мА и внутреннее сопротивление R0 . Чему равна чувствительность к напряжению Su.
III. Милливольтметр магнитоэлектрической системы со шкалой αmax делений имеет внутреннее сопротивление R0 и чувствительность к току SI. Определите чувствительность прибора к напряжению Su , цену деления (постоянную) по току и напряжению СI, СU и верхний предел измерения по току Iв и напряжению Uв.
IV. Каким вольтметром будет точнее измерено напряжение U, если имеются три электромеханических вольтметра со следующими характеристиками:
 1. Класса точности К1, верхний предел измерения Uв1.
1. Класса точности К1, верхний предел измерения Uв1.
 2. Класса точности К2, диапазон измерения UД2.
2. Класса точности К2, диапазон измерения UД2.
 3. Класса точности К3, диапазон измерения UД3.
3. Класса точности К3, диапазон измерения UД3.
V. Для измерения частоты f можно использовать три частотомера:
1. Электромеханический класса точности К1 с диапазонам измерения fд1 и номинальным значением f ном.
2. Электронный класса точности К2 с верхним пределом измерения fв2.
3. Цифровой класса точности с3/ d 3 = 0,5/0,2 с верхним пределом измерения fв3
Какой из этих частотомеров следует выбрать, чтобы измерение было выполнено точнее?
VI. Определите значение аддитивной и мультипликативной составляющих погрешностей цифрового вольтметра класса точности 0,1/0,05 при показании U на верхнем пределе измерения Uв
VII. Определить значение аддитивной и мультипликативной составляющих погрешностей цифрового моста класса точности 0,05/0,02 при верхнем пределе измерения Rв и показаний R /
Защита практической работы.
 Теоретический опрос.
Теоретический опрос.
 1. Виды измерения: прямые, косвенные, совокупные, совместные;
1. Виды измерения: прямые, косвенные, совокупные, совместные;
 2. Основные характеристики измерения;
2. Основные характеристики измерения;
 3. Методы измерении.
3. Методы измерении.
 4. Сущность погрешности;
4. Сущность погрешности;
 5. Виды погрешности измерений: методическая погрешность, инструментальная погрешность, субъективная погрешность;
5. Виды погрешности измерений: методическая погрешность, инструментальная погрешность, субъективная погрешность;
 6. Формы погрешности: абсолютная и относительная;
6. Формы погрешности: абсолютная и относительная;
 7. Погрешности измерения физической величины: статистическая погрешность, динамическая погрешность, систематическая погрешность, случайная погрешность;
7. Погрешности измерения физической величины: статистическая погрешность, динамическая погрешность, систематическая погрешность, случайная погрешность;
 8. Погрешность средств измерения;
8. Погрешность средств измерения;
| Таблица вариантов для задач практической работы по погрешностям | |||||||||||||||||||||||||
| № задачи |
Задача №2 |
Задача № 3 |
Задача №4 |
Задача №5 |
Задача №6 |
Задача №7 | |||||||||||||||||||
| № варианта | Iв (А) | I (А) | Iд (А) | Х (дел/мА) | Rо (Ом) | α max | Rо (Ом) | S I (дел/мА) | U | К1 | К2 | К3 | Uв1 | Uд2 | Uд3 | ƒ | К1 | К2 | ƒном | ƒв2 | ƒв3 | U | Uв | R | Rв |
| 1 | 5 | 4 | 3,8 | 10 | 5 | 150 | 5 | 10 | 20 | 1,0 | 0.5 | 1,5 | 25 | -20÷20 | 20÷40 | 50 | 1,5 | 1 | 50 | 100 | 500 | 5 | 10 | 500 | 1000 |
| 2 | 6 | 5 | 5,05 | 11 | 11 | 200 | 15 | 20 | 50 | 2,5 | 1.5 | 1 | 50 | -50 ÷50 | 30÷70 | 70 | 1 | 1,5 | 75 | 100 | 600 | 4 | 8 | 400 | 800 |
| 3 | 7 | 3 | 2,75 | 25 | 30 | 250 | 20 | 15 | 30 | 0,5 | 0.5 | 0,2 | 30 | -30÷30 | 10÷40 | 100 | 0,5 | 1 | 150 | 100 | 550 | 6 | 12 | 1000 | 2000 |
| 4 | 6 | 2 | 1,98 | 15 | 18 | 300 | 25 | 30 | 50 | 0,1 | 0.1 | 0,5 | 60 | -50÷ 50 | 40÷80 | 110 | 1,5 | 0,5 | 110 | 120 | 200 | 10 | 20 | 600 | 1200 |
| 5 | 5 | 4 | 4,05 | 10 | 8 | 350 | 30 | 15 | 25 | 2,5 | 1.5 | 1,5 | 30 | -25÷25 | 0÷25 | 105 | 1 | 1,5 | 105 | 110 | 500 | 15 | 30 | 2000 | 4000 |
| 6 | 7 | 7 | 6,9 | 30 | 30 | 300 | 35 | 20 | 10 | 0,2 | 0.5 | 0,1 | 30 | -10÷10 | 0÷15 | 90 | 0,5 | 0,1 | 180 | 200 | 300 | 20 | 40 | 500 | 1000 |
| 7 | 8 | 6 | 5,99 | 20 | 20 | 250 | 40 | 10 | 15 | 2,5 | 1.5 | 2,5 | 20 | -15÷15 | 0÷40 | 80 | 1,5 | 0,1 | 80 | 100 | 350 | 25 | 50 | 1200 | 2000 |
| 8 | 6 | 5 | 4,08 | 15 | 20 | 200 | 35 | 30 | 10 | 0,1 | 0.2 | 0,2 | 50 | -10÷10 | 0÷20 | 60 | 1 | 0,5 | 65 | 100 | 550 | 30 | 60 | 800 | 1600 |
| 9 | 5 | 4 | 4,08 | 20 | 15 | 150 | 30 | 15 | 50 | 0,5 | 0.5 | 0,5 | 60 | -50÷50 | 0÷50 | 40 | 0,5 | 1 | 80 | 40 | 400 | 35 | 70 | 300 | 600 |
| 10 | 7 | 7 | 5,98 | 10 | 15 | 125 | 25 | 25 | 40 | 2,5 | 1 | 1,5 | 50 | -40÷40 | 0÷80 | 50 | 0,1 | 1 | 100 | 50 | 500 | 20 | 40 | 450 | 900 |
| 11 | 8 | 6 | 6,08 | 20 | 10 | 120 | 20 | 20 | 20 | 0,5 | 0.2 | 0,2 | 20 | -20÷25 | 0÷25 | 70 | 1 | 1,5 | 70 | 100 | 600 | 15 | 30 | 1500 | 3000 |
| 12 | 6 | 5 | 4,98 | 30 | 15 | 115 | 15 | 25 | 20 | 1,5 | 2 | 0,5 | 40 | -20÷30 | 0÷50 | 90 | 1,5 | 0,5 | 95 | 100 | 650 | 10 | 20 | 600 | 1200 |
| 13 | 5 | 4 | 3,97 | 15 | 5 | 110 | 10 | 20 | 10 | 1,0 | 1 | 1 | 15 | -10÷20 | 0÷30 | 100 | 1 | 0,5 | 110 | 150 | 800 | 6 | 12 | 400 | 800 |
| 14 | 8 | 8 | 7,99 | 25 | 15 | 100 | 5 | 15 | 20 | 0,5 | 1 | 1,5 | 35 | -20÷20 | 10÷50 | 110 | 1,5 | 1 | 110 | 120 | 700 | 4 | 8 | 500 | 1000 |
| 15 | 7 | 6 | 5,8 | 30 | 20 | 110 | 10 | 10 | 20 | 1,5 | 1 | 0,5 | 25 | -25÷25 | 15÷30 | 115 | 0,5 | 0,5 | 120 | 110 | 750 | 5 | 10 | 1000 | 2000 |
Практическая работа №4
Дата: 2019-02-19, просмотров: 992.