Содержание
7.1. Решение систем нелинейных и линейных уравнений 2
7.1.1. Функция root (f(z),z,a,b) 2
7.1.2. Функция Polyroots() 6
7.1.3. Использование вычислительного блока Given – Find () 7
7.1.4. Использование функции Given – MinErr () 10
7.1.5. использование функции Lsolve(). 10
7.1.6. Использование метода Гаусса. 11
7.1.7. Использование метода Крамера. 12
7.1.8. Использование матричного метода. 14
7.1.9. Исследование системы неоднородных уравнений. 15
7.2. Решение дифференциальных уравнений-- 18
7.2.1. Решение ДУ первого порядка- 18
7.2.1.1. Использование функции Odesolve() 18
7.2.1.2. Использование функции rkfixed- 20
7.2.2. Решение систем ДУ. 21
7.2.2.1. Использование встроенных функций Rkfixed(), Rkadapt(),Bulstoer(). 22
7.2.3. Решение ДУ высших порядков- 24
7.2.3.1. Использование функции Given-Odesolve() 24
7.2.3.2. Использование встроенных функций Rkfixed(), Rkadapt(),Bulstoer(). 25
7.3. Интерполирование и функции предсказания-- 30
7.3.1. Линейная интерполяция- 30
7.3.2. Кубическая сплайн-интерполяция- 32
7.3.3. Линейное предсказание- 34
7.3.4. Использование функции регрессии- 35
7.3.4.1. Линейная регрессия- 36
7.3.4.2. Полиномиальная регрессия- 37
Контрольные вопросы-- 37
Лекция 7
Использование встроенных функций
Использование встроенных функций, реализующих численные методы интегрированной среды MathCAD, проиллюстрируем на примерах расчета различных задач.
Функция Polyroots()
Если f(x) представляет собой полином и его коэффициенты, начиная со свободного члена, можно представить в виде вектора v, то для поиска одновременно всех корней полинома можно использовать функцию polyroots(v).
Построим алгоритм нахождения корней полинома с помощью встроенной функции polyroots(). Функция polyroots() находит все возможные корни уравнения и выводит их пользователю в виде вектора.
Рассмотрим пример использования функции polyroots ().
· Пусть дан полином 3-й степени. Запишем его в виде:

· Зададим точность:
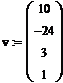
· Запишем коэффициенты полинома в вектор v, начиная с коэффициента, стоящего у неизвестного низшей степени, т.е. x0. Тогда вектор v примет вид:
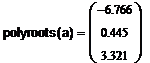
· После того, как были проведены все вышеперечисленные действия можно применить встроенную функцию polyroots(вектор коэффициентов).
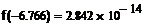
· Чтобы сделать проверку, необходимо в исходную функцию поочередно подставить корни уравнения. Т.е.:
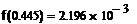
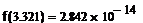

Если вычисления проведены правильно, то в результате проверки значение функции в корнях уравнения должны быть равны 0 или числам близким к 0 (все зависит от заданной точности).
Подробнее о функциях:
- решение обыкновенных дифференциальных уравнений (odesolve, rkfixed);
- решение гладких систем (Bulstoer);
- решение жестких систем (Stiffb, Stiffr);
- решение медленно изменяющихся систем (Rkadapt);
- нахождение последней точки на интегрируемом интервале (bulstoer, rkadapt, stiffb, stiffr);
- решение краевых задач с двумя ограничениями (bvalfit, sbval);
- решение дифференциальных уравнений в частных производных (relax, multigrid);
Решение ДУ первого порядка
Рассмотрим некоторые из часто используемых функций.
Решение систем ДУ.
MathCad 200x требует, чтобы система ОДУ была представлены в виде:
 |
Также должны быть представлены начальные условия в виде:

,где b, c, t – числа.
Для решения систем ОДУ применяются следующие функции:
· Rkfixed(y0,t0,t1,M,D) – реализует метод Рунге – Кутты с фиксированным шагом;
· Rkadapt(y0,t0,t1,M,D) – реализует метод Рунге – Кутты с переменным шагом;
· Bulstoer(y0,t0,t1,M,D) – реализует метод Булирша-Штера.
где y0 – вектор начальных значений в точке t0 размера N×1;
t0 – начальная точка расчета;
t1 – конечная точка расчета;
М – число шагов, на которых численный метод находит решение;
D – векторная функция размера N×1 двух аргументов – скалярного t и векторного y. При этом у – искомая векторная функция аргумента t того же размера N×1.
Решение ДУ высших порядков
В MathCad 2001 можно решать ДУ высших порядков как с помощью вычислительного блока Given-Odesolve(), так и путем сведения их к системам уравнений первого порядка. Рассмотрим эти два способа решения ДУ высших порядков подробнее.
Линейная интерполяция
При выполнении линейной интерполяции MathCAD соединяет смежные точки табличной функции прямыми линиями, представляя функцию в виде ломаной линии. Тогда по такой функции можно определить любые промежуточные значения в заданном интервале. Эти вычисления выполняются встроенной функцией linterp(). Она имеет формат
linterp(vx,vy,t)
где vx – вектор, состоящий из значений х, заданных в таблице исходных данных (замечание: элементы вектора х должны располагаться в порядке возрастания)
vy – вектор состоящий из значений у заданных в таблице исходных данных (замечание: определенному);
t – аргумент, при котором нужно найти промежуточное значение y. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания.
При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp() не предназначена и за пределами области определения может вести себя непредсказуемо.
Построим график функции используя линейную интерполяцию. Алгоритм построения графика состоит из нескольких этапов:
· Пусть дана таблица исходных данных:
· 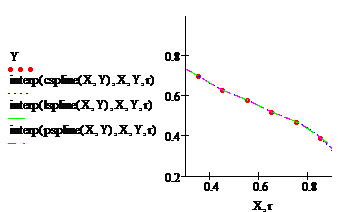
Определение вектора неизвестных (берется из таблицы данных. В нашем случае Х можно записать в виде ранжированной переменной, потому что нетрудно увидеть зависимость между последующим и предыдущим значением каждого из Х):
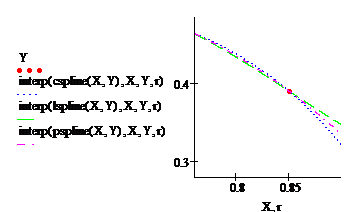
· Определение вектора Y (берется из таблицы данных):

· Встроенная функция linterp() вычисляет значение в конкретной точке (последний параметр функции), но так как нам необходимо построить график, то мы заменим параметр t неизвестной (например, r), не имеющей дискретного значения, и подставим эту переменную в нижний местозаполнитель декартовой системы координат (плоский график). построим график, отформатируем его по своему усмотрению:
A(r):= linterp(X,Y,r)

Чтобы вычислить значение графика в какой – либо точке, необходимо поставить вместо r число. Замечание: данные действия необходимо производить вне графической зоны.
Пример: Вычислим значение функции, построенной с помощью линейной интерполяции в точке 2.1:

Линейное предсказание
Интерполяция дает возможность по значениям табличной функции находить значения в промежуточных точках. Однако бывают случаи, когда необходимо оценить табличную функцию за пределами ее области данных. В MathCAD имеется функция predict(), позволяющая это сделать. Формат функции:
predict(vy,m,n)
где vy – вектор табличных значений функции (элементы вектора vy должны быть взяты через равные интервалы);
m – число последних исходных значений табличной функции, по которым выполняется прогноз;
n – число предсказанных значений табличной функции.
Рассмотрим применение функции предсказания на примере:
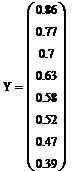
Пусть дана таблица данных
· Определение вектора Y (берется из таблицы данных):

· Определение m, число известных значений Y по которым будет построена экстраполяция, в нашем случае m = 8;
· Определение n, число значений Y, по которым строится экстраполяция + количество точек которое необходимо предсказать. В нашем случае n = 13.
· Построим график функции предсказания. Для наглядности построим на одном графике исходную функцию (построим по точкам) и функцию предсказания, причем таким образом, чтобы последняя являлась продолжением первой функции. Для этого необходимо провести некоторые манипуляции:
Ø Так как мы имеем 8 значений исходных данных, то будем строить исходную функцию в 8 – ми точках:
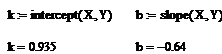
Ø Так как мы собираемся строить экстраполяцию для 13 – ти точек, то:
Ø Построим график функций. Причем необходимо обратить внимание, что мы сдвинули начало координат для функции предсказания на 8 точек вправо (потому что исходная функция кончается на 8 – й точке) с помощью выражения j+8.

Линейная регрессия
При выполнении линейной регрессии табличная функция заменяется линейной зависимостью, описываемой уравнением y=kx+b (уравнение прямой). Значения k и b можно найти с помощью функций:
· Slope (vx,vy) – возвращает наклон линии регрессии (коэффициент k);
· Intercept (vx,vy) – возвращает смещение по оси ординат (значение b) линии регрессии.
Или
· line(vx, vy) – возвращает вектор коэффициентов, стоящих при неизвестных начиная с младшей степени.
 |
Выполним линейную регрессию для функции заданной таблично. Рассмотрим таблицу данных из предыдущих примеров:
· Составим вектор неизвестных Х:

· Составим вектор значений функции Y(X):

· Рассчитаем коэффициенты, стоящие при неизвестных:

C(X):=b*X+k
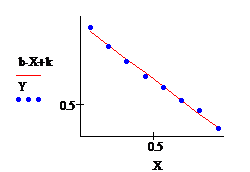
· Подставим значения коэффициентов в уравнение прямой и построим график. на графике изобразим начальные данные в виде точек и уравнение линейной регрессии:

Коэффициенты уравнения линейной регрессии выбраны таким образом, чтобы среднеквадратическое отклонение было минимальным.
Полиномиальная регрессия
При выполнении полиномиальной регрессии табличная функция заменяется полиномом n-й степени. Для этой цели используются функции:
Regress (vx,vy,n) – возвращает вектор, требуемый функцией interp(), чтобы найти полином порядка n, который наилучшим образом приближает данные vx и vy. На практике не следует использовать n>4. Функция regress() пытается одним полиномом приблизить все данные, что не дает хороших результатов для табличных функций, не связанных одной полиномиальной зависимостью;
Loess (vx,vy,span) – возвращает вектор, требуемой функцией interp(), чтобы найти набор полиномов второго порядка, который наилучшем образом приближает данные из vx и vy. Аргумент span (span>0,) определяет, насколько большие окрестности функция loess() будет использовать при выполнении локального приближения. Вместо одного полином, как это дает функция regress(), функция loess() создает различные полиномы второго порядка в зависимости от расположения на кривой, исследуя данные в малой окрестности, определяемой параметром span (по умолчанию span=0.75);
Interp(vs,vx,vy,x) – возвращает интерполируемое значение y, соответствующее х. Вектор vs вычисляется функцией regress() или loess().
Пример
Контрольные вопросы
1. Методика отыскания корней нелинейных уравнений в системе MathCAD. Приведите примеры.
2. Методика решения систем нелинейных уравнений в MathCAD’е. Приведите примеры.
3. Действия пользователя, направленные на поиск корней уравнений.
4. Как графически проверить наличие действительных корней системы двух уравнений?
5. Как задается точность поиска корней?
6. Как найти корни при аналитических преобразованиях?
7. Перечислите способы решения системы линейных уравнений в системе MathCAD.
8. Методика решения обыкновенных дифференциальных уравнений в системе MathCAD.
9. Выполните пример 7.1 в системе MathCAD
10. Как решить систему двух дифференциальных уравнений?
11. Методика выполнения линейной интерполяции в системе MathCAD.
12. Методика выполнения интерполяции кубическим сплайном.
13. Сущность линейного предсказания и ее реализация.
14. Сущность линейной регрессии и ее реализация.
15. Сущность полиномиальной регрессии и ее реализация.
Содержание
7.1. Решение систем нелинейных и линейных уравнений 2
7.1.1. Функция root (f(z),z,a,b) 2
7.1.2. Функция Polyroots() 6
7.1.3. Использование вычислительного блока Given – Find () 7
7.1.4. Использование функции Given – MinErr () 10
7.1.5. использование функции Lsolve(). 10
7.1.6. Использование метода Гаусса. 11
7.1.7. Использование метода Крамера. 12
7.1.8. Использование матричного метода. 14
7.1.9. Исследование системы неоднородных уравнений. 15
7.2. Решение дифференциальных уравнений-- 18
7.2.1. Решение ДУ первого порядка- 18
7.2.1.1. Использование функции Odesolve() 18
7.2.1.2. Использование функции rkfixed- 20
7.2.2. Решение систем ДУ. 21
7.2.2.1. Использование встроенных функций Rkfixed(), Rkadapt(),Bulstoer(). 22
7.2.3. Решение ДУ высших порядков- 24
7.2.3.1. Использование функции Given-Odesolve() 24
7.2.3.2. Использование встроенных функций Rkfixed(), Rkadapt(),Bulstoer(). 25
7.3. Интерполирование и функции предсказания-- 30
7.3.1. Линейная интерполяция- 30
7.3.2. Кубическая сплайн-интерполяция- 32
7.3.3. Линейное предсказание- 34
7.3.4. Использование функции регрессии- 35
7.3.4.1. Линейная регрессия- 36
7.3.4.2. Полиномиальная регрессия- 37
Контрольные вопросы-- 37
Лекция 7
Использование встроенных функций
Использование встроенных функций, реализующих численные методы интегрированной среды MathCAD, проиллюстрируем на примерах расчета различных задач.
Дата: 2018-09-13, просмотров: 9803.