Содержание
Введение
1. Понятие производства и производственных функций
2. Виды и типы производственных функций
2.1 Изокванта и ее типы
2.2 Оптимальная комбинация ресурсов
2.3 Функции предложения и их свойства
3. Практическое применение производственной функции
3.1 Моделирование издержек и прибыли предприятия (фирмы)
3.2 Методы учета научно-технического прогресса
Заключение
Список литературы
Введение
Мной выбрана тема «Сущность, модели, границы применения метода производственной функции». Эта тема актуальна из – за того, что этот метод позволяет ответить на главный вопрос, который стоит перед экономистами на предприятиях и предпринимателями – «А что будет, если…». Именно благодаря этому методу можно произвести расчёты получения возможной прибыли в различных условиях, и понять какую прибыль мы можем получить – от гарантированного минимума до возможного максимума, не проводя эксперименты в реальном времени и не рискуя своими финансами.
А что же такое производственная функция? Обратимся к словарю яндекса и получим следующее:
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ (ПФ)[1] [production function] (то же: функция производства) — экономико-математическое уравнение, связывающее переменные величины затрат (ресурсов) с величинами продукции (выпуска). ПФ применяются для анализа влияния различных сочетаний факторов на объем выпуска в определенный момент времени (статический вариант П. ф.) и для анализа, а также прогнозирования соотношения объемов факторов и объема выпуска в разные моменты времени (динамический вариант Пф.) на различных уровнях экономики — от фирмы (предприятия) до народного хозяйства в целом (агрегированная ПФ, в которой выпуском служит показатель совокупного общественного продукта или национального дохода и т. п.). В отдельной фирме, корпорации и т. п. ПФ описывает максимальный объем выпуска продукции, которую они в состоянии произвести при каждом сочетании используемых факторов производства. Она может быть представлена множеством изоквант, связанных с различными уровнями объема производства.
Такой вид ПФ, когда устанавливается явная зависимость объема производства продукции от наличия или потребления ресурсов, называется функцией выпуска.
В частности, широко используются функции выпуска в сельском хозяйстве, где с их помощью изучается влияние на урожайность таких факторов, как, напр., разные виды и составы удобрений, методы обработки почвы. Наряду с подобными ПФ используются обратные к ним функции производственных затрат. Они характеризуют зависимость затрат ресурсов от объемов выпуска продукции (строго говоря, они обратны только к ПФ с взаимозаменяемыми ресурсами). Частными случаями ПФ можно считать функцию издержек (связь объема продукции и издержек производства), инвестиционную функцию (зависимость потребных капиталовложений от производственной мощности будущего предприятия) и др.
Математически ПФ могут быть представлены в различных формах — от столь простых, как линейная зависимость результата производства от одного исследуемого фактора, до весьма сложных систем уравнений, включающих рекуррентные соотношения, которыми связываются состояния изучаемого объекта в разные периоды времени.
Наиболее широко распространены мультипликативно-степенные формы представления ПФ. Их особенность состоит в следующем: если один из сомножителей равен нулю, то результат обращается в нуль. Легко заметить, что это реалистично отражает тот факт, что в большинстве случаев в производстве участвуют все анализируемые первичные ресурсы и без любого из них выпуск продукции оказывается невозможным. В самой общей форме (она называется канонической) эта функция записывается так:
или 
Здесь коэффициент А, стоящий перед знаком умножения, учитывает размерность, он зависит от избранной единицы измерений затрат и выпуска. Сомножители от первого до n-го могут иметь различное содержание в зависимости от того, какие факторы оказывают влияние на общий результат (выпуск). Напр., в ПФ, которая применяется для изучения экономики в целом, можно в качестве результативного показателя принять объем конечного продукта, а сомножителей — численность занятого населения x1, сумму основных и оборотных фондов x2, площадь используемой земли x3. Только два сомножителя у функции Кобба—Дугласа, с помощью которой была сделана попытка оценить связь таких факторов, как труд и капитал, с ростом национального дохода США в 20—30-е гг. ХХ в.:
N = A · Lα · Kβ,
где N — национальный доход; L и K — соответственно объемы приложенного труда и капитала.
Степенные коэффициенты (параметры) мультипликативно-степенной ПФ показывают ту долю в процентном приросте конечного продукта, которую вносит каждый из сомножителей (или на сколько процентов возрастет продукт, если затраты соответствующего ресурса увеличить на один процент); они являются коэффициентами эластичности производства относительно затрат соответствующего ресурса. Если сумма коэффициентов составляет 1, это означает однородность функции: она возрастает пропорционально росту количества ресурсов. Но возможны и такие случаи, когда сумма параметров больше или меньше единицы; это показывает, что увеличение затрат приводит к непропорционально большему или непропорционально меньшему росту выпуска (Эффект масштаба).
В динамическом варианте применяются разные формы ПФ. Напр., (в 2-факторном случае): Y(t) = A(t) Lα(t) Kβ(t), где множитель A(t) обычно возрастает во времени, отражая общий рост эффективности производственных факторов в динамике.
Логарифмируя, а затем, дифференцируя по t указанную функцию, можно получить соотношения между темпами прироста конечного продукта (национального дохода) и прироста производственных факторов (темпы прироста переменных принято здесь описывать в процентах).
Дальнейшая “динамизация” ПФ может заключаться в использовании переменных коэффициентов эластичности.
Описываемые ПФ соотношения носят статистический характер, т. е. проявляются только в среднем, в большой массе наблюдений, поскольку реально на результат производства воздействуют не только анализируемые факторы, но и множество неучитываемых. Кроме того, применяемые показатели как затрат, так и результатов неизбежно являются продуктами сложного агрегирования (напр., обобщенный показатель трудовых затрат в макроэкономической функции вбирает в себя затраты труда разной производительности, интенсивности, квалификации и т. д.).
Особая проблема — учет в макроэкономических ПФ фактора технического прогресса (подробнее см. в ст. “Научно-технический прогресс”). С помощью ПФ изучается также эквивалентная взаимозаменяемость факторов производства (см. Эластичность замещения ресурсов), которая может быть либо неизменной, либо переменной (т. е. зависимой от объемов ресурсов). Соответственно функции делят на два вида: с постоянной эластичностью замены (CES — Constant Elasticity of Substitution) и с переменной (VES — Variable Elasticity of Substitution) (см. ниже).
На практике применяются три основных метода определения параметров макроэкономических ПФ: на основе обработки временных рядов, на основе данных о структурных элементах агрегатов и о распределении национального дохода. Последний метод называется распределительным.
При построении ПФ необходимо избавляться от явлений мультиколлинеарности параметров и автокорреляции — в противном случае неизбежны грубые ошибки.
Приведем некоторые важные ПФ (см. также Кобба—Дугласа функция).
Линейная п. ф.:
P = a1x1 + ... + anxn,
где a1, ..., an — оцениваемые параметры модели: здесь факторы производства замещаемы в любых пропорциях.
Функция CES:
P = A [(1 – α) K-b + αL-b]-c/b,
в этом случае эластичность замещения ресурсов не зависит ни от K, ни от L и, следовательно, постоянна:
Отсюда и происходит название функции.
Функция CES, как и функция Кобба— Дугласа, исходит из допущения о постоянном убывании предельной нормы замещения используемых ресурсов. Между тем эластичность замещения капитала трудом и, наоборот, труда капиталом в функции Кобба—Дугласа, равная единице, здесь может принимать различные значения, не равные единице, хотя и является постоянной. Наконец, в отличие от функции Кобба—Дугласа логарифмирование функции CES не приводит ее к линейному виду, что вынуждает использовать для оценки параметров более сложные методы нелинейного регрессионного анализа.
Изокванта и ее типы
При моделировании потребительского спроса один и тот же уровень полезности различных комбинаций потребительских благ графически отображается с помощью кривой безразличия.
В экономико-математических моделях производства каждая технология графически может быть представлена точкой, координаты которой отражают минимально необходимые затраты ресурсов K и L для производства данного объема выпуска. Множество таких точек образуют линию равного выпуска, или изокванту . Таким образом, производственная функция графически представляется семейством изоквант. Чем дальше от начала координат расположена изокванта, тем больший объем производства она отражает. В отличие от кривой безразличия, каждая изокванта характеризует количественно определенный объем выпуска.
Рис. 1. Изокванты, соответствующие различному объему производства
На рис. 1 представлено три изокванты, соответствующие объему производства в 200, 300 и 400 единиц продукции. Можно сказать, что для выпуска 300 единиц продукции необходимо K 1 единиц капитала и L 1 единиц труда или K 2 единиц капитала и L 2 единиц труда, или любая другая их комбинация из того множества, которое представлено изоквантой Y 2 = 300.
В общем случае в множестве X допустимых наборов производственных факторов выделяется подмножество X c , называемое изоквантой производственной функции, которое характеризуется тем, что для всякого вектора 
справедливо равенство
Таким образом, для всех наборов ресурсов, соответствующих изокванте, оказываются равными объемы выпускаемой продукции. По существу изокванта представляет собой описание возможности взаимной замены факторов в процессе производства продукции, обеспечивающей неизменный объем производства. В связи с этим оказывается возможным определить коэффициент взаимной замены ресурсов, используя дифференциальное соотношение вдоль любой изокванты
Отсюда коэффициент эквивалентной замены пары факторов j и k равен:
Полученное соотношение показывает, что если производственные ресурсы замещаются в отношении, равном отношению приростных продуктивностей, то количество производимой продукции остается неизменным. Нужно сказать, что знание производственной функции позволяет охарактеризовать масштабы возможности осуществить взаимную замену ресурсов в эффективных технологических способах. Для достижения этой цели служит коэффициент эластичности замены ресурсов по продукции
который вычисляется вдоль изокванты при неизменном уровне затрат прочих производственных факторов. Величина sjk представляет собой характеристику относительного изменения коэффициента взаимной замены ресурсов при изменении соотношения между ними. Если отношение взаимозаменяемых ресурсов изменится на sjk процентов, то коэффициент взаимной замены sjk изменится на один процент. В случае линейной производственной функции коэффициент взаимной замены остается неизменным при любом соотношении используемых ресурсов и поэтому можно считать, что эластичность s jk = 1. Соответственно большие значения sjk свидетельствуют о том, что возможна большая свобода в замене производственных факторов вдоль изокванты и при этом основные характеристики производственной функции (продуктивности, коэффициент взаимозамены) будут меняться очень слабо.
Для степенных производственных функций для любой пары взаимозаменяемых ресурсов справедливо равенство s jk = 1. В практике прогнозирования и предплановых расчетов часто используются функции постоянной эластичности замены (СЕS), имеющие вид:
Для такой функции коэффициент эластичности замены ресурсов
и не меняется в зависимости от объема и отношения затрачиваемых ресурсов. При малых значениях s jk ресурсы могут заменять друг друга лишь в незначительных размерах, а в пределе при s jk = 0 они теряют свойство взаимозаменяемости и выступают в процессе производства лишь в постоянном отношении, т.е. являются взаимодополняющими. Примером производственной функции, описывающей производство в условиях использования взаимодополняющих ресурсов, является функция выпусказатрат, которая имеет вид
где a j постоянный коэффициент ресурсоотдачи j -того производственного фактора. Нетрудно видеть, что производственная функция такого типа определяет выпуск по узкому месту на множестве используемых производственных факторов. Различные случаи поведения изоквант производственных функций для различных значений коэффициентов эластичности замены представлены на графике (рис. 2).
Представление эффективного технологического множества с помощью скалярной производственной функции оказывается недостаточным в тех случаях, когда нельзя обойтись единственным показателем, описывающим результаты деятельности производственного объекта, но необходимо использовать несколько ( М ) выходных показателей. В этих условиях можно использовать векторную производственную функцию
Рис. 2. Различные случаи поведения изоквант
Важное понятие предельной (дифференциальной) продуктивности вводится соотношением
Аналогичное обобщение допускают все остальные главные характеристики скалярных ПФ.
Подобно кривым безразличия изокванты также подразделяются на различные типы.
Для линейной производственной функции вида
где Y объем производства; A , b 1 , b 2 параметры; K , L затраты капитала и труда, и полном замещении одного ресурса другим изокванта будет иметь линейную форму (рис. 3).
Для степенной производственной функции
изокванты будут иметь вид кривых (рис. 4).
Если изокванта отражает лишьодин технологический способ производства данного продукта, то труд и капитал комбинируются в единственно возможном сочетании (рис. 5).
Рис. 3. Изокванты линейного типа
| 
Рис. 4. Изокванты степенной производственной функции
| 
Рис. 45. Изокванты при жесткой дополняемости ресурсов
|
Рис. 6. Ломаные изокванты
Такие изокванты иногда называют изоквантами леонтьевского типа по имени американского экономиста В.В. Леонтьева, который положил такой тип изокванты в основу разработанного им метода inputoutput (затратывыпуск).
Ломаная изокванта предполагает наличие ограниченного количества технологий F (рис. 6).
Изокванты подобной конфигурации используются в линейном программировании для обоснования теории оптимального распределения ресурсов. Ломаные изокванты наиболее реалистично представляют технологические возможности многих производственных объектов. Однако в экономической теории традиционно используют главным образом кривые изокванты, которые получаются из ломаных при увеличении числа технологий и увеличении соответственно точек излома.
Объемы и затраты
Цены и прибыли
Продолжение таблицы 1
Четвертый столбец характеризует значения указанных выше маргинальных издержек МС , которые показывают, во сколько обходится производство одного дополнительного изделия в данной ситуации. Нетрудно заметить, что маргинальные издержки возрастают по мере роста производства, что хорошо согласуется с положением, высказанным в начале этого параграфа. При рассмотрении таблицы следует обратить внимание на то, что оптимальные объемы находятся точно на пересечении строки (маргинальные издержки МС) и столбца (цена p) с равными их значениями, что совершенно аккуратно соотносится с правилом оптимальности, установленным выше.
Проведенный выше анализ относится к обстановке совершенной конкуренции, когда производитель не может повлиять своими действиями на систему цен, и поэтому цена p на товар y выступает в модели производителя как экзогенная величина.
В случае же несовершенной конкуренции производитель может оказывать непосредственное влияние на цену. В особенности это относится к монопольному производителю товара, который формирует цену из соображения разумной рентабельности.
Рассмотрим фирму с линейной функцией издержек, которая определяет цену таким образом, чтобы прибыль составляла определенный процент (долю 0 < g < 1) от валового дохода, т.е.
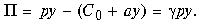
Отсюда имеем
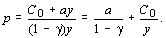
Валовой доход
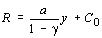
и производство оказывается безубыточным, начиная с самых малых объемов производства ( y w 0). Легко видеть, что цена зависит от объема, т.е. p = p ( y ), и при увеличении объема производства ( у ) цена товара уменьшается, т.е. p' ( y ) < 0. Это положение имеет место для монополиста и в общем случае.
Требование максимизации прибыли для монополиста имеет вид
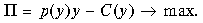
Предполагая по-прежнему, что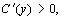 
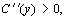имеем уравнение для нахождения оптимального выпуска ( 
):
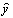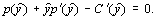
Полезно заметить, что оптимальный выпуск монополиста ( 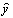) как правило, не превосходит оптимального выпуска конкурентного производителя 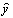в формуле, помеченной звездочкой (С.37).
Более реалистичная (но также простая) модель фирмы используется для того, чтобы учесть ресурсные ограничения, которые играют очень большую роль в хозяйственной деятельности производителей. В модели выделяется один наиболее дефицитный ресурс (рабочая сила, основные фонды, редкий материал, энергия и т.п.) и предполагается, что фирма может его использовать не более чем в количестве Q . Фирма может производить n различных продуктов. Пусть y 1 , ..., y j , ..., y n искомые объемы производства этих продуктов; p 1 , ..., p j , ..., p n их цены. Пусть также q цена единицы дефицитного ресурса. Тогда валовой доход фирмы равен
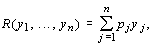
а прибыль составит
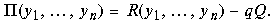
Легко видеть, что при фиксированных q и Q задача о максимизации прибыли преобразуется в задачу максимизации валового дохода.
Предположим далее, что функция издержек ресурса для каждого продукта C j ( y j ) обладает теми же свойствами, которые были высказаны выше для функции С ( у ). Таким образом, C j ' ( y j ) > 0 и C j '' ( y j ) > 0.
В окончательном виде модель оптимального поведения фирмы с одним ограниченным ресурсом следующая:
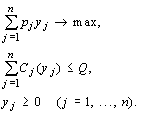
Нетрудно видеть, что в достаточно общем случае решение этой оптимизационной задачи находится путем исследования системы уравнений:
| (**) |
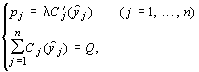
Где j множитель Лагранжа.
Заметим, что соотношение
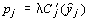
является по существу аналогом отмеченного выше совпадения в оптимальной точке маргинального дохода и маргинальных издержек. В случае квадратичных функций издержек
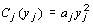
из системы уравнений (**) имеем:
| (***) |
Заметим, что оптимальный выбор фирмы зависит от всей совокупности цен на продукты ( p 1 , ..., p n ), причем этот выбор является однородной функцией системы цен, т.е. при одновременном изменении цен в одинаковое число раз оптимальные выпуски 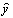не изменяются. Нетрудно видеть также, что из уравнений, помеченных звездочками (***), следует, что при увеличении цены на продукт n (при неизменных ценах на другие продукты) его выпуск следует увеличить с целью получения максимальной прибыли, так как
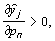
а производство остальных товаров уменьшится, так как
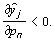
Эти соотношения в совокупности показывают, что в данной модели все продукты являются конкурирующими. Из формулы (***) вытекает также очевидное соотношение
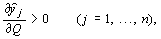
т.е. при увеличении объема ресурса (капиталовложений, рабочей силы и т.п.) оптимальные выпуски увеличиваются.
Можно привести ряд простых примеров, которые помогут лучше понять правило оптимального выбора фирмы по принципу максимума прибыли:
1) пусть n = 2; p 1 = p 2 = 1; a 1 = a 2 = 1; Q = 0,5; q = 0,5.
Тогда из (***) имеем:
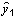= 0,5; 
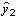= 0,5; П = 0,75; 
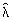= 1;
2) пусть теперь все условия остались прежними, но удвоилась цена на первый продукт: p 1 = 2.
Тогда оптимальный по прибыли план фирмы: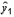 
= 0,6325; 
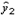= 0,3162.
Ожидаемая максимальная прибыль заметно возрастает: П = 1,3312; 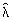= 1,58;
3) заметим, что в предыдущем примере 2 фирма должна изменить объемы производств, увеличив производство первого и уменьшив производство второго продукта. Предположим, однако, что фирма не гонится за максимальной прибылью и не станет менять налаженное производство, т.е. выберет программу y 1 = 0,5; y 2 = 0,5.
Оказывается, что в этом случае прибыль составит П = 1,25. Это означает, что при повышении цен на рынке фирма может получить значительное увеличение прибыли без изменения плана выпуска.
Заключение
В заключении хотелось бы рассказать о производственной функции Кобба – Дугласа.
Возникновение теории производственных функций принято относить к 1927 г., когда появилась статья американских ученых экономиста П. Дугласа (P. Douglas) и математика Д. Кобба (D. Cobb) «Теория производства». В этой статье, была предпринята попытка, эмпирическим путем определить влияние затрачиваемого капитала и труда на объем выпускаемой продукции в обрабатывающей промышленности США.
Как уже было сказано, производственная функция отражает функциональную связь между объёмом эффективно используемых факторов производства (трудом и имущественным капиталом) и с их помощью достигаемым выпуском при существующем техническом и организационном знании.
При субституционной производственной функции производство может быть увеличено за счёт повышения количественной характеристики одного из факторов, в то время как количественная характеристика другого фактора остаётся без изменения, в другом варианте же производство остаётся без изменения при различных количественных комбинациях факторов труда и имущественного капитала.
Субстиционная производственная функция имеет, в общем следующее выражение:
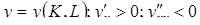
где:
K – число производственного капитала
L – число производственных трудовых часов или, другими словами, число производственных единиц гуманного капитала
На основе условно введённой субстиционности факторов производства можно сделать следующие два вывода относительно функциональной взаимосвязи данных факторов:
При прочих равных увеличение одного из факторов производства ведёт к увеличению выпуска – первая производная положительна.
Однако предельная производительность возрастающего фактора уменьшается с увеличением величины данного фактора – вторая производная отрицательна.
Уровень организационных и технических знаний отображается в соответствующих формах взаимодействий факторов. В рассматриваемом случае уровень знаний постоянен, т.е. в данных рамках предполагается отсутствие технического прогресса. Таким образом, субстиционная функция производства может быть представлена в виде следующего изображения, отражающего взаимосвязь между количеством труда и выпуском при заданном количестве имущественного капитала (рисунок 1):
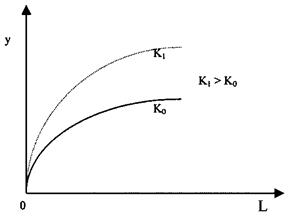
Рис. 17. Связь между производством и производственным трудом
Каждое увеличение количественного параметра имущественного капитала означает смещение кривой вверх и одновременного увеличения предельной производительности труда при заданном количестве рабочей силы, т.е. на основе вытекающего непосредственно из описанного вывода означает и более высокую величину выпуска при увеличении производственного фактора «труд»: кривая OK1 на рисунке показывает более крутой наклон по сравнению с кривой OK0 при любом числе занятых трудом.
С увеличением количественного параметра имущественного капитала увеличивается и средняя производительности труда, которая является частным от деления величины выпуска на величину затраченного труда. Однако при этом уменьшается коэффициент труда, определяющий среднее количество затраченного труда на каждую единицу выпуска и являющийся таким образом обратной величиной средней производительности труда.
Величина имущественного капитала принимается в рамках данного кратковременного анализа как экзогенно заданная, поэтому в модели и описании не учитывается технический прогресс, а также эффект увеличения производственных мощностей за счёт инвестиций.
В 1927 г. Пол Дуглас обнаружил, что если совместить графики зависимости от времени логарифмов показателей реального объема выпуска (y), капитальных затрат (К) и затрат труда (L), то расстояния от точек графика показателей выпуска до точек графиков показателей затрат труда и капитала будут составлять постоянную пропорцию. Затем он обратился к Чарльзу Коббу с просьбой найти математическую зависимость, обладающую такой особенностью, и Кобб предложил следующую субституционную функцию:
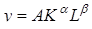
Эта функция была предложена примерно 30 годами раньше Филипом Уикстидом (Wicksteed), но они были первыми, кто использовал для ее построения эмпирические данные.
Однако при больших значениях K и L эта функция не имеет экономического смысла, т.к. выпуск все время возрастает при возрастании затрат.
Кинетическая функция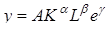 
(где g - норма технического прогресса за единицу времени) получена умножением функции Кобба-Дугласа на eg, что снимает данную проблему и делает функцию Кобба-Дугласа экономически интересной.
Эластичность выпуска продукции по капиталу и труду равна соответственно a и b, так как
,
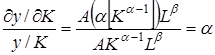и аналогичным образом легко показать, что (dy / d L)/(y /L) равно b.
Следовательно, увеличение затрат капитала на 1% приведет к росту выпуска продукции на a процентов, а увеличение затрат труда на 1% приведет к росту выпуска на b процентов. Можно предположить, что обе величины a и b находятся между нулем и единицей. Они должны быть положительными, так как увеличение затрат производственных факторов должно вызывать рост выпуска. В то же время, вероятно, они будут меньше единицы, так как разумно предположить, что уменьшение эффекта от масштаба производства приводит к более медленному росту выпуска продукции, чем затрат производственных факторов, если другие факторы остаются постоянными.
Если a и b в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства (y увеличивается в той же пропорции, что и К и L). Если их сумма меньше, чем единица, то имеет место убывающий эффект от масштаба производства (y увеличивается в меньшей пропорции, чем К и L).
В соответствии с допущением о конкурентности рынков факторов производства и b имеют дальнейшую интерпретацию как прогнозируемые доли дохода, полученного соответственно за счет капитала и труда. Если рынок труда имеет конкурентный характер, то ставка заработной платы (w) будет равна предельному продукту труда (dy / d L):
.
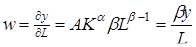Следовательно, общая сумма заработной платы (wL) будет равна b y, а доля труда в общем выпуске продукции (wL/Y) составит постоянную величину b. Аналогичным образом норма прибыли выражается через dy / dK:
,
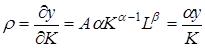и, следовательно, общая прибыль (r К) будет равна a y, а доля прибыли будет постоянной величиной a.
Существует ряд проблем по применению такой функции, особенно в тех случаях, когда она используется для экономики в целом. В частности, даже в тех случаях, когда между выпуском продукции, производственным оборудованием и трудом в производственном процессе существует технологическая зависимость, то совершенно необязательно, что подобная зависимость существует тогда, когда указанные факторы комбинируются в масштабах экономики в целом. Во-вторых, даже если такая зависимость для экономики в целом существует, то нет никаких оснований считать, что она будет иметь простую форму.
Список литературы
1. 50 лекций по микроэкономике/ Институт "Экономическая Школа", 2002.
2. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: Инфра-М, 2001.
3. Институциональная экономика: курс лекций/ Кузьминов Я.И. М.: Высшая Школа Экономики, 2009.
4. Трактат по политической экономии/ Жан-Батист Сэй. Сайт "Библиотека экономической и деловой литературы".
5. Основы экономической теории. / Под ред. Камаева В.Д. - М.: Изд. МГТУ, 2006.
6. Основы экономической теории (макроэкономика): Учебное пособие./ Кравцова Г.Ф., Цветков Н.И., Островская Т.И. Хабаровск: ДВГУПС, 2001. http://www.dvgups.ru/METDOC/EKMEN/ETEOR/EK_TEOR/METOD/O_EK_TEOR/KRAV1.HTM
7. Учебник по основам экономической теории. / Под ред. В.Д.Камаева. - М.: Владос: Изд-во МГТУ им. Н. Э. Баумана, 2006.
8. Самуэльсон П. Экономика.: Пер. с англ. - М.: Прогресс, 1964.
9. Экономика предприятия: Учебник/ под ред. О.И. Волкова. – 4-е изд., перераб. и доп. – Финансы и статистика, 2000
10. Ресурс интернет - .http://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-1199.htm
[1] http://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-1199.htm
Содержание
Введение
1. Понятие производства и производственных функций
2. Виды и типы производственных функций
2.1 Изокванта и ее типы
2.2 Оптимальная комбинация ресурсов
2.3 Функции предложения и их свойства
3. Практическое применение производственной функции
3.1 Моделирование издержек и прибыли предприятия (фирмы)
3.2 Методы учета научно-технического прогресса
Заключение
Список литературы
Введение
Мной выбрана тема «Сущность, модели, границы применения метода производственной функции». Эта тема актуальна из – за того, что этот метод позволяет ответить на главный вопрос, который стоит перед экономистами на предприятиях и предпринимателями – «А что будет, если…». Именно благодаря этому методу можно произвести расчёты получения возможной прибыли в различных условиях, и понять какую прибыль мы можем получить – от гарантированного минимума до возможного максимума, не проводя эксперименты в реальном времени и не рискуя своими финансами.
А что же такое производственная функция? Обратимся к словарю яндекса и получим следующее:
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ (ПФ)[1] [production function] (то же: функция производства) — экономико-математическое уравнение, связывающее переменные величины затрат (ресурсов) с величинами продукции (выпуска). ПФ применяются для анализа влияния различных сочетаний факторов на объем выпуска в определенный момент времени (статический вариант П. ф.) и для анализа, а также прогнозирования соотношения объемов факторов и объема выпуска в разные моменты времени (динамический вариант Пф.) на различных уровнях экономики — от фирмы (предприятия) до народного хозяйства в целом (агрегированная ПФ, в которой выпуском служит показатель совокупного общественного продукта или национального дохода и т. п.). В отдельной фирме, корпорации и т. п. ПФ описывает максимальный объем выпуска продукции, которую они в состоянии произвести при каждом сочетании используемых факторов производства. Она может быть представлена множеством изоквант, связанных с различными уровнями объема производства.
Такой вид ПФ, когда устанавливается явная зависимость объема производства продукции от наличия или потребления ресурсов, называется функцией выпуска.
В частности, широко используются функции выпуска в сельском хозяйстве, где с их помощью изучается влияние на урожайность таких факторов, как, напр., разные виды и составы удобрений, методы обработки почвы. Наряду с подобными ПФ используются обратные к ним функции производственных затрат. Они характеризуют зависимость затрат ресурсов от объемов выпуска продукции (строго говоря, они обратны только к ПФ с взаимозаменяемыми ресурсами). Частными случаями ПФ можно считать функцию издержек (связь объема продукции и издержек производства), инвестиционную функцию (зависимость потребных капиталовложений от производственной мощности будущего предприятия) и др.
Математически ПФ могут быть представлены в различных формах — от столь простых, как линейная зависимость результата производства от одного исследуемого фактора, до весьма сложных систем уравнений, включающих рекуррентные соотношения, которыми связываются состояния изучаемого объекта в разные периоды времени.
Наиболее широко распространены мультипликативно-степенные формы представления ПФ. Их особенность состоит в следующем: если один из сомножителей равен нулю, то результат обращается в нуль. Легко заметить, что это реалистично отражает тот факт, что в большинстве случаев в производстве участвуют все анализируемые первичные ресурсы и без любого из них выпуск продукции оказывается невозможным. В самой общей форме (она называется канонической) эта функция записывается так:
или
Здесь коэффициент А, стоящий перед знаком умножения, учитывает размерность, он зависит от избранной единицы измерений затрат и выпуска. Сомножители от первого до n-го могут иметь различное содержание в зависимости от того, какие факторы оказывают влияние на общий результат (выпуск). Напр., в ПФ, которая применяется для изучения экономики в целом, можно в качестве результативного показателя принять объем конечного продукта, а сомножителей — численность занятого населения x1, сумму основных и оборотных фондов x2, площадь используемой земли x3. Только два сомножителя у функции Кобба—Дугласа, с помощью которой была сделана попытка оценить связь таких факторов, как труд и капитал, с ростом национального дохода США в 20—30-е гг. ХХ в.:
N = A · Lα · Kβ,
где N — национальный доход; L и K — соответственно объемы приложенного труда и капитала.
Степенные коэффициенты (параметры) мультипликативно-степенной ПФ показывают ту долю в процентном приросте конечного продукта, которую вносит каждый из сомножителей (или на сколько процентов возрастет продукт, если затраты соответствующего ресурса увеличить на один процент); они являются коэффициентами эластичности производства относительно затрат соответствующего ресурса. Если сумма коэффициентов составляет 1, это означает однородность функции: она возрастает пропорционально росту количества ресурсов. Но возможны и такие случаи, когда сумма параметров больше или меньше единицы; это показывает, что увеличение затрат приводит к непропорционально большему или непропорционально меньшему росту выпуска (Эффект масштаба).
В динамическом варианте применяются разные формы ПФ. Напр., (в 2-факторном случае): Y(t) = A(t) Lα(t) Kβ(t), где множитель A(t) обычно возрастает во времени, отражая общий рост эффективности производственных факторов в динамике.
Логарифмируя, а затем, дифференцируя по t указанную функцию, можно получить соотношения между темпами прироста конечного продукта (национального дохода) и прироста производственных факторов (темпы прироста переменных принято здесь описывать в процентах).
Дальнейшая “динамизация” ПФ может заключаться в использовании переменных коэффициентов эластичности.
Описываемые ПФ соотношения носят статистический характер, т. е. проявляются только в среднем, в большой массе наблюдений, поскольку реально на результат производства воздействуют не только анализируемые факторы, но и множество неучитываемых. Кроме того, применяемые показатели как затрат, так и результатов неизбежно являются продуктами сложного агрегирования (напр., обобщенный показатель трудовых затрат в макроэкономической функции вбирает в себя затраты труда разной производительности, интенсивности, квалификации и т. д.).
Особая проблема — учет в макроэкономических ПФ фактора технического прогресса (подробнее см. в ст. “Научно-технический прогресс”). С помощью ПФ изучается также эквивалентная взаимозаменяемость факторов производства (см. Эластичность замещения ресурсов), которая может быть либо неизменной, либо переменной (т. е. зависимой от объемов ресурсов). Соответственно функции делят на два вида: с постоянной эластичностью замены (CES — Constant Elasticity of Substitution) и с переменной (VES — Variable Elasticity of Substitution) (см. ниже).
На практике применяются три основных метода определения параметров макроэкономических ПФ: на основе обработки временных рядов, на основе данных о структурных элементах агрегатов и о распределении национального дохода. Последний метод называется распределительным.
При построении ПФ необходимо избавляться от явлений мультиколлинеарности параметров и автокорреляции — в противном случае неизбежны грубые ошибки.
Приведем некоторые важные ПФ (см. также Кобба—Дугласа функция).
Линейная п. ф.:
P = a1x1 + ... + anxn,
где a1, ..., an — оцениваемые параметры модели: здесь факторы производства замещаемы в любых пропорциях.
Функция CES:
P = A [(1 – α) K-b + αL-b]-c/b,
в этом случае эластичность замещения ресурсов не зависит ни от K, ни от L и, следовательно, постоянна:
Отсюда и происходит название функции.
Функция CES, как и функция Кобба— Дугласа, исходит из допущения о постоянном убывании предельной нормы замещения используемых ресурсов. Между тем эластичность замещения капитала трудом и, наоборот, труда капиталом в функции Кобба—Дугласа, равная единице, здесь может принимать различные значения, не равные единице, хотя и является постоянной. Наконец, в отличие от функции Кобба—Дугласа логарифмирование функции CES не приводит ее к линейному виду, что вынуждает использовать для оценки параметров более сложные методы нелинейного регрессионного анализа.
Понятие производства и производственных функций
Под производством понимается любая деятельность по использованию природных, материально-технических и интеллектуальных ресурсов для получения как материальных, так и нематериальных благ.
С развитием человеческого общества характер производства меняется. На ранних стадиях развития человечества господствовали природные, натуральные, естественно возникшие элементы производительных сил. Да и сам человек в это время в большей степени был продуктом природы. Производство в этот период получило название натурального.
С развитием средств производства начинают преобладать исторически созданные материально-технические элементы производительных сил. Это эпоха капитала. В настоящее время решающее значение имеют знания, технологии, интеллектуальные ресурсы самого человека. Наша эпоха это эпоха информатизации, эпоха господства научно-технических элементов производительных сил. Владение знаниями, новыми технологиями имеет решающее значение для производства. Во многих развитых странах ставится задача всеобщей информатизации общества. Потрясающими темпами развивается всемирная компьютерная сеть Internet.
Традиционно роль общей теории производства выполняет теория материального производства, понимаемая как процесс превращения производственных ресурсов в продукт. Основными производственными ресурсами являются труд ( L ) и капитал ( K ). Способы производства или существующие производственные технологии определяют, какой объем продукции производится при заданных количествах труда и капитала. Математически существующие технологии выражаются через производственную функцию . Если обозначить объем выпускаемой продукции через Y , то производственную функцию можно записать
Y = f ( K , L ).
Это выражение означает, что объем выпуска является функцией количества капитала и количества труда. Производственная функция описывает множество существующих в данный момент технологий. Если изобретается лучшая технология, то при тех же затратах труда и капитала объем выпуска увеличивается. Следовательно, изменения в технологии изменяют и производственную функцию. Методологически теория производства во многом симметрична теории потребления. Однако если в теории потребления основные категории измеряются лишь субъективно или вообще пока не подлежат измерению, то основные категории теории производства имеют объективную основу и могут быть измерены в определенных натуральных или стоимостных единицах.
Несмотря на то, что понятие производство может представиться очень широким, нечетко выраженным и даже расплывчатым, поскольку в реальной жизни под производством понимается и предприятие, и стройка, и сельскохозяйственная ферма, и транспортное предприятие, и очень крупная организация типа отрасли народного хозяйства, тем не менее, экономико-математическое моделирование выделяет нечто общее, присущее всем этим объектам. Этим общим является процесс преобразования первичных ресурсов (производственных факторов) в конечные результаты процесса. Поэтому основным исходным понятием в описании экономического объекта становится технологический способ, который представляется обычно как вектор v затратвыпуска, включающий в себя перечисление объемов затрачиваемых ресурсов (вектор x) и сведения о результатах их преобразования в конечные продукты или другие характеристики (прибыль, рентабельность и т.п.) (вектор y):
v = ( x ; y ).
Размерность векторов x и y , а также способы их измерения (в натуральных или стоимостных единицах) существенно зависят от изучаемой проблемы, от уровней, на которых ставятся те или иные задачи экономического планирования и управления. Совокупность векторов технологических способов, которые могут служить описанием (с допустимой точки зрения исследователя точностью) производственного процесса, реально осуществимого на некотором объекте, называется технологическим множеством V данного объекта. Для определенности мы будем полагать, что размерность вектора затрат x равна N , а вектора выпуска y соответственно M . Таким образом, технологический способ v является вектором размерности ( M + N ), а технологическое множество 
Среди всех технологических способов, осуществимых на объекте, особое место занимают способы, которые выгодно отличаются от всех прочих тем, что они требуют либо меньших затрат при одинаковом выпуске, либо соответствуют большему выпуску при одинаковых затратах. Те из них, которые занимают в определенном смысле предельное положение в множестве V , представляют особый интерес, поскольку они являются описанием допустимого и предельно выгодного реального производственного процесса.
Скажем, что вектор 
предпочтительнее, чем вектор 
с обозначением 
если выполняются следующие условия:
1) 
2) 
и при этом имеет место по крайней мере одно из двух:
а) существует такой номер i 0 , что 
б) существует такой номер j 0 , что 
Технологический способ 
называется эффективным, если он принадлежит технологическому множеству V и не существует другого вектора 
который был бы предпочтительнее 
. Приведенное определение означает, что эффективными считаются те способы, которые не могут быть улучшены ни по одной затратной компоненте, ни по одной позиции выпускаемой продукции, без того чтобы не перестать быть допустимыми. Множество всех технологически эффективных способов обозначим через V* . Оно является подмножеством технологического множества V или совпадает с ним. По существу задача планирования хозяйственной деятельности производственного объекта может быть интерпретирована как задача выбора эффективного технологического способа, наилучшим образом соответствующего некоторым внешним условиям. При решении такой задачи выбора достаточно существенным оказывается представление о самом характере технологического множества V , а также его эффективного подмножества V* .
В ряде случаев оказывается возможным допустить в рамках фиксированного производства возможность взаимозаменяемости некоторых ресурсов (различных видов топлива, машин и работников и т.п.). При этом математический анализ подобных производств основывается на предпосылке о континуальном характере множества V , а следовательно, на принципиальной возможности представления вариантов взаимной замены при помощи непрерывных и даже дифференцируемых функций, определенных на V . Указанный подход получил свое наибольшее развитие в теории производственных функций.
С помощью понятия эффективного технологического множества производственную функцию (ПФ) можно определить как отображение
y = f ( x ),
где 
V* .
Указанное отображение, вообще говоря, является многозначным, т.е. множество f ( x ) содержит более чем одну точку. Однако для многих реалистичных ситуаций производственные функции оказываются однозначными и даже, как сказано выше, дифференцируемыми. В наиболее простом случае производственная функция есть скалярная функция N аргументов:
Здесь величина y имеет, как правило, стоимостный характер, выражая объем производимой продукции в денежном выражении. В качестве аргументов выступают объемы затрачиваемых ресурсов при реализации соответствующего эффективного технологического способа. Таким образом, приведенное соотношение описывает границу технологического множества V ,поскольку при данном векторе затрат ( x 1 , ..., x N ) производить продукции, в количестве большем, чем y , невозможно, а производство продукции в количестве меньшем, чем указанное, соответствует неэффективному технологическому способу. Выражение для производственной функции оказывается возможным использовать для оценки эффективности принятого на данном предприятии методе хозяйствования. В самом деле, для заданного набора ресурсов можно определить фактический выпуск продукции и сравнить его с рассчитанным по производственной функции. Полученная разница дает полезный материал для оценки эффективности в абсолютном и относительном измерении.
Производственная функция представляет собой очень полезный аппарат плановых расчетов, и поэтому в настоящее время развит статистический подход к построению производственных функций для конкретных хозяйственных единиц. При этом обычно используется некоторый стандартный набор алгебраических выражений, параметры которых находятся при помощи методов математической статистики. Такой подход означает, в сущности, оценку производственной функции на основе неявного предположения о том, что наблюдаемые производственные процессы являются эффективными. Среди разнообразных типов производственных функций наиболее часто применяются линейные функции вида
поскольку для них легко решается задача оценивания коэффициентов по статистическим данным, а также степенные функции
для которых задача нахождения параметров сводится к оцениванию линейной формы путем перехода к логарифмам.
В предположении о дифференцируемости производственной функции в каждой точке множества X возможных комбинаций затрачиваемых ресурсов полезно рассмотреть некоторые связанные с ПФ величины.
В частности, дифференциал
представляет собой изменение стоимости выпускаемой продукции при переходе от затрат набора ресурсов x = ( x 1 , ..., x N ) к набору x + dx = ( x 1 + dx 1 , ..., x N + dx N ) при условии сохранения свойства эффективности соответствующих технологических способов. Тогда величину частной производной
можно трактовать как предельную (дифференциальную) ресурсоотдачу или, иными словами, коэффициент предельной продуктивности, который показывает, на сколько увеличится выпуск продукции в связи с увеличением затрат ресурса с номером j на малую единицу. Величина предельной продуктивности ресурса допускает истолкование как верхний предел цены p j , которую производственный объект может уплатить за дополнительную единицу j -того ресурса с тем, чтобы не оказаться в убытках после ее приобретения и использования. В самом деле, ожидаемый прирост продукции в этом случае составит
и, следовательно, соотношение
позволит получить дополнительную прибыль.
В коротком периоде, когда один ресурс рассматривается как постоянный, а другой как переменный, большинство производственных функций обладают свойством убывающего предельного продукта. Предельным продуктом переменного ресурса называют прирост общего продукта в связи с увеличением применения данного переменного ресурса на единицу.
Предельный продукт труда можно записать как разность
MPL = F ( K , L + 1) - F ( K , L ),
где MPL предельный продукт труда.
Предельный продукт капитала можно также записать как разность
MPK = F ( K + 1, L ) - F ( K , L ),
где MPK предельный продукт капитала.
Характеристикой производственного объекта является также величина средней ресурсоотдачи (продуктивности производственного фактора)
имеющего ясный экономический смысл количества выпускаемой продукции в расчете на единицу используемого ресурса (производственного фактора). Величина, обратная к ресурсоотдаче
обычно называется ресурсоемкостью, поскольку она выражает количество ресурса j , необходимое для производства одной единицы продукции в стоимостном выражении. Весьма употребительны и понятны такие термины, как фондоемкость, материалоемкость, энергоемкость, трудоемкость, рост которых обычно связывают с ухудшением состояния экономики, а их снижение рассматривается как благоприятный результат.
Частное от деления дифференциальной продуктивности на среднюю
называется коэффициентом эластичности продукции по производственному фактору j и дает выражение относительного прироста продукции (в процентах) при относительном приросте затрат фактора на 1%. Если E j ё 0, то происходит абсолютное снижение выпуска продукции при увеличении потребления фактора j; такая ситуация может иметь место при использовании технологически неподходящих продуктов или режимов. Например, излишнее потребление топлива приведет к излишнему повышению температуры и необходимая для производства продукта химическая реакция не пойдет. Если 0 < E j ё 1, то каждая последующая дополнительная единица затрачиваемого ресурса вызывает меньший дополнительный прирост продукции, чем предыдущая.
Если E j > 1, то величина приростной (дифференциальной) продуктивности превосходит среднюю продуктивность. Таким образом, дополнительная единица ресурса увеличивает не только объем выпускаемой продукции, но и среднюю характеристику ресурсоотдачи. Так процесс повышения фондоотдачи происходит, когда вводятся в действие весьма прогрессивные, эффективные машины и приборы. Для линейной производственной функции коэффициент a j численно равен величине дифференциальной продуктивности j -того фактора, а для степенной функции показатель степени a j имеет смысл коэффициента эластичности по j -тому ресурсу.
Дата: 2019-05-29, просмотров: 199.
