Назовите известные Вам типовые комбинационные цифровые устройства и охарактеризуйте их работу.
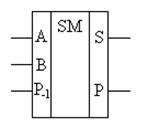
Шифраторы, а)дешифраторы, мультиплексоры, сумматоры.
Под КЦУ мы будем понимать цифровое устройство (ЦУ), которое обеспечивает преобразование совокупности цифровых сигналов Х в выходные сигналы Y. Для формирования цифровых выходных сигналов используются ЦУ двух классов:
ЦУ, выходные сигналы у которых в некоторый момент времени tn зависят только от совокупности (комбинации) сигналов Х, присутствующих на их входах в тот же момент времени tn, и не зависят от входных сигналов, поступивших в предшествующие моменты времени. Иными словами, ЦУ этого класса “не помнит” предыстории поступления сигналов на его входы. Такие ЦУ принято называть комбинационными (КЦУ);
ЦУ, выходные сигналы у которых в момент tn определяются не только комбинациями входных сигналов Х, воздействующих в тот же момент tn, но и сигналами, поступающими на входы в предшествующие моменты времени. В состава таких ЦУ обязательно присутствуют элементы памяти, внутреннее состояние которых отражает предысторию поступления последовательности входных сигналов. Подобные ЦУ принято называть последовательностными (ПЦУ) или конечными автоматами.
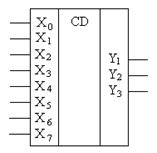
Дешифратор (рис А) – это устройство, предназначенное для преобразования двоичного кода в напряжение логической единицы (логического нуля) на том выходе, номер которого совпадает со значением двоичного кода на входе. При n входах в полном дешифраторе имеется 2n выходов, т.е. для каждой комбинации входных сигналов имеется соответствующий выход. Дешифратор, у которого при n входах число выходов меньше 2n, называется неполным. Другое название дешифратора - декодер. Принцип работы полного трехразрядного дешифратора рассмотрим на примере его таблицы истинности.
| Входы | Выходы | |||||||||
| X3 | X2 | X1 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| и т. д. | ||||||||||
Шифраторы(рисБ) выполняют задачу обратную той, которую выполняют дешифраторы: появление логической единицы (логического нуля) на определенном входе приводит к появлению соответствующей кодовой комбинации на выходе. Также как и дешифраторы, шифраторы бывают полными и неполными. Работа восьмивходового полного шифратора задается следующей таблицей истинности:
Входы
Выходы
и т. д.
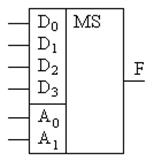
Мультиплексор – (рис В) комбинационное цифровое устройство, которое обеспечивает передачу на единственный выход F одного из нескольких входных сигналов Dj в соответствии с поступающим адресным кодом Ai. При наличии n адресных входов можно реализовать M=2n комбинаций адресных сигналов, каждая из которых обеспечивает выбор одного из M входов. Чаще всего используются мультиплексоры «из 4 в 1» (n=2, M=4), «из 8 в 1» (n=3, M=8), «из 16 в 1» (n=4, M=16). Правило работы мультиплексора «из 4 в 1» можно задать таблицей истинности:
 |
| Входы | 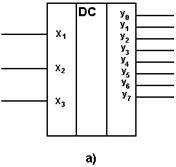 Выход Выход
| |
| A1 | A0 | F |
| 0 | 0 | D0 |
| 0 | 1 | D1 |
| 1 | 0 | D2 |
| 1 | 1 | D3 |
 | |||
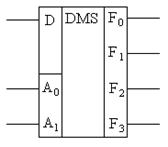 |
Демультиплексор выполняет функцию, обратную мультиплексору, т.е. в соответствии с принятой адресацией Ai направляет информацию с единственного входа D на один из M выходов Fj. При этом на остальных выходах будут логические нули (единицы). Принцип работы демультиплексора «из 1 в 4» иллюстрируется таблицей истинности:
| Входы | Выходы | ||||
| A1 | A0 | F3 | F2 | F1 | F0 |
| 0 | 0 | 0 | 0 | 0 | D |
| 0 | 1 | 0 | 0 | D | 0 |
| 1 | 0 | 0 | D | 0 | 0 |
| 1 | 1 | D | 0 | 0 | 0 |
Сумматоры – это класс КЦУ, выполняющих операцию арифметического сложения двух двоичных n-разрядных чисел. Сумматоры бывают полными и неполными. Неполный сумматор или полусумматор - это комбинационное устройство с двумя входами и двумя выходами, выполняющее операцию сложения двух одноразрядных чисел в соответствии с таблицей истинности, где А и В – входные одноразрядные числа, S п/см. – выход суммы, а P п/см. – выход переноса в старший разряд:
 |
| Входы | Выходы | ||
| А | В | S п/см. | P п/см. |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
В чем состоят особенности статистических характеристик случайных величин? Назовите числовые характеристики случайных процессов и приведите алгоритмы измерения этих величин. Приведите аналитическое выражение, графическое изображение и структурную схему системы для измерения функции распределения.
Статистические измерения, или измерения вероятностных характеристик случайных процессов, — это широкий круг методов и средств, применяемых в различных областях народного хозяйства.
Под вероятностными характеристиками случайных процессов будем понимать математическое ожидание, дисперсию, законы распределения вероятностей, корреляционные и спектральные функции.
На рис. 10.18, а изображен стационарный случайный процесс; на рис. 10.18, б -- нестационарный случайный процесс с переменным во времени математическим ожиданием; на рис. 10.18, в — нестационарный случайный процесс с переменной во времени дисперсией; на рис. 10.18, г — нестационарный случайный процесс с переменным во времени математическим ожиданием и дисперсией
Если рассматривать стационарный случайный процесс, приведенный на рис. 10.19, а, то функция распределения определяется как вероятность Р в интервале - оо < Х( f ) < x , где ;с может изменяться от - оо до + оо;
Значение функции распределения при изменении х в вышеуказанных пределах изменяется от 0 до 1:
Эмпирическая функция распределения — это функция F *( X )9 определяющая для каждого значения х относительную частоту события X < х, т.е.
а — стационарный; б — нестационарный с переменным математическим ожиданием; в — нестационарный с переменной дисперсией; г — нестационарный с переменным математическим ожиданием и дисперсией
а — стационарный случайный процесс; б — функция распределения; в — плотность распределения 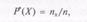
где X -- статистическое распределение частот; пх — число наименьших вариантов п\п — объем выборки.
Плотность распределения вероятностей получают путем дифференцирования Р(Х) по х: 
Измерение математического ожидания. Структурная схема устройства,
Измерение дисперсии. приведен один из вариантов построения средств измерений дисперсии случайного процесса дисперсиометром:
Структурная схема средств измерения математического ожидания случайного процесса
Сущность метода наименьших квадратов
Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений
Изложим идею этого способа, ограничиваясь случаем линейной зависимости. Пусть требуется установить зависимость между двумя величинами x и y, Произведем обследование n видов и представим результаты исследования в виде таблицы:
| x | x1 | ... | xn |
| y | y1 | ... | yn |
Из анализа таблицы нелегко обнаружить наличие и характер зависимости между x и y. Поэтому обратимся к графику. Допустим, что точки, взятые из таблицы (опытные точки) группируются около некоторой прямой линии. Тогда можно предположить, что между x и y существует линейная зависимостьy= ax+b, где a и b - коэффициенты, подлежащие определению,y - теоретическое значение ординаты. Проведя прямую “на глаз”, можно графически найти b и a=tg , однако это будут весьма неточные результаты. Для нахождения a, b применяют метод наименьших квадратов.
Перепишем уравнение искомой прямой в виде ax + b -y=0. Точки, построенные на основе опытных данных, вообще говоря, не лежат на этой прямой. Поэтому если подставить в уравнение прямой вместо x иy заданные величины xi и yi, то окажется, что левая часть уравненияравна какой-то малой величине i=yi -yi; а именно: для первой точкиax1 + b - y1 = 1, для второй - ax2 + b - y2 = 2, для последней axn + b - yn = n. Величины 1, 2,..., n, не равные нулю, называются погрешностями. Геометрически это разность между ординатой точки на прямой и ординатой опытной точки с той же абсциссой. Погрешности зависят от выбранного положения прямой, т.е. от a и b. Требуется подобрать a и b таким образом, чтобы эти погрешности были возможно меньшими по абсолютной величине. Способ наименьших квадратов состоит в том, что a и b выбираются из условия, чтобы сумма квадратов погрешностей u = 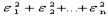 была минимальной. Если эта сумма квадратов окажется минимальной, то и сами погрешности будут в среднем малыми по абсолютной величине. Подставим в выражение для u вместо i их значения.
была минимальной. Если эта сумма квадратов окажется минимальной, то и сами погрешности будут в среднем малыми по абсолютной величине. Подставим в выражение для u вместо i их значения.
u = (ax1 + b - y1) 2 + (ax2 + b - y2) 2 +... + ( axn + b - yn)2, или u = u(a,b), где xi, yi известные величины, a и b - неизвестные, подлежащиеопределению. Выберем a и b так, чтобы u(a,b) имело наименьшеезначение. Необходимые условия экстремума 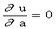 ,
, 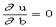 . Имеем:
. Имеем:  = 2(ax1 + b - y1)x1 +... +2 (ax1 + b - y1)xn,
= 2(ax1 + b - y1)x1 +... +2 (ax1 + b - y1)xn, 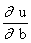 = 2(ax1 + b - y1) +... + 2 (ax1 + b - y1). Получаем систему:
= 2(ax1 + b - y1) +... + 2 (ax1 + b - y1). Получаем систему:
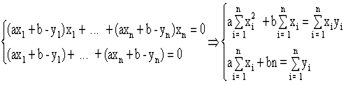 .
.
Эта система называется нормальной системой метода наименьших квадратов. Из нее находим a и b и затем подставляем их в эмпирическую формулу y = ax + b.
Дата: 2019-05-29, просмотров: 233.