Тема 6. Теоретико-игровые модели принятия решений

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Понятие об игровых моделях

В управленческой деятельности при принятии решения приходится противодействовать другой стороне, которая может преследовать противоположные или иные цели, добиваться других путей достижения цели, препятствовать теми или иными действиями или состояниями внешней среды достижению намеченной цели. Причем эти противодействия противоположной стороны могут носить пассивный или активный характер. В таких условиях необходимо учитывать возможные варианты поведения противоположной стороны, ответные действия, возможную реакцию и соответственно возможные исходы.

Возможные варианты поведения обеих сторон и их исходов для каждого сочетания альтернатив и состояний можно представить в виде математической модели, которая называется игрой [19].

Если в качестве противоположности выступает неактивная, пассивная сторона, которая явно активно не противодействует достижению намеченной цели, то такие игры называются играми с «природой» [19]. Такой стороной в управлении являются неизвестность поведения подчиненных, клиентов, партнеров, недостаточность информации и т.п.

В других ситуациях противоположная сторона активно, сознательно может противостоять достижению намеченной цели. В подобных случаях происходит столкновение противоположных интересов, мнений, целей. Такие ситуации называются конфликтными, а принятие решений в конфликтной ситуации затрудняется из-за неопределенности поведения противника. Известно, что противник сознательно стремится предпринять наименее выгодные для вас действия, чтобы обеспечить себе наибольший успех. Неизвестно, в какой мере противник умеет оценить обстановку и возможные последствия, как он оценивает ваши возможности и намерения. Обе стороны конфликта не могут точно предсказать взаимные действия. Несмотря на такую неопределенность, принимать решения приходится каждой стороне конфликта [19].

Необходимость обоснования оптимальных решений в конфликтных ситуациях привела к возникновению теории игр.

Теория игр – это математическая теория конфликтных ситуаций. Основными ограничениями этой теории являются предположение о полной «идеальной» разумности противника и принятие при разрешении конфликта наиболее осторожного решения [19].

Основные понятия теории игр

Конфликтующие стороны называются игроками, одна реализация игры – партией, исход игры – выигрышем или проигрышем [19].

Развитие игры во времени происходит последовательно, по этапам или ходам. Ходом в теории игр называют выбор одного из предусмотренных правилами игры действия и его реализацию. Ходы бывают личные и случайные. Личным ходом называют сознательный выбор игроком одного из возможных вариантов действия и его осуществление. Случайным ходом называют выбор, осуществляемый не волевым решением игрока, а каким-либо механизмом случайного выбора (бросание монеты, пасовка, сдача карт и т.п.) [19].

Одним из основных понятий теории игр является стратегия. Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе этого игрока в зависимости от ситуации, сложившейся в процессе игры. Оптимальной стратегией игрока называется такая стратегия, которая при многократном повторении игры, содержащей личные и случайные ходы, обеспечивает игроку максимально возможный средний выигрыш или минимально возможный средний проигрыш [19].

В большинстве конфликтных ситуаций при выборе разумной стратегии приходится принимать во внимание не один, а несколько показателей и факторов. Причем стратегия, оптимальная по одному показателю, необязательно будет оптимальной и по другим. В зависимости от причин, вызывающих неопределенность исходов, игры можно разделить на следующие основные группы [19]:

- комбинаторные игры, в которых правила дают в принципе возможность каждому игроку проанализировать все разнообразные варианты своего поведения и, сравнив эти варианты, избрать тот из них, который ведет к наилучшему для этого игрока исходу. Неопределенность исхода связана обычно с тем, что количество возможных вариантов поведения (ходов) слишком велико и практически игрок не в состоянии их всех перебрать и проанализировать;

- азартные игры, в которых исход оказывается неопределенным в силу влияния различных случайных факторов. Азартные игры состоят только из случайных ходов, при анализе которых применяется теория вероятностей. Азартными играми теория игр не занимается;

- стратегические игры, в которых полная неопределенность исхода вызвана тем, что каждый из игроков, принимая решение о выборе предстоящего хода, не знает, какой стратегии будут придерживаться другие участники игры, причем незнание игрока о поведении и намерениях партнеров носит принципиальный характер, так как отсутствует информация о последующих действиях противника (партнера).

Существуют игры, сочетающие в себе свойства комбинаторных и азартных игр, стратегичность игр может сочетаться с комбинаторностью и т.д.

В игре могут сталкиваться интересы двух или более игроков. Если в игре участвуют два игрока, игра называется парной, если число игроков больше двух – множественной. Участники множественной игры могут образовывать коалиции (постоянные или временные). Множественная игра с двумя постоянными коалициями превращается в парную. Парные игры получили наибольшее распространение в практике анализа игровых ситуаций [19].

Различают игры и по сумме выигрыша. Игра называется игрой с нулевой суммой, если каждый игрок выигрывает за счет других, а сумма выигрыша одной стороны равна проигрышу другой. В парной игре с нулевой суммой интересы игроков прямо противоположны. Парная игра с нулевой суммой называется антагонистической игрой. Игры, в которых выигрыш одного игрока и проигрыш другого не равны между собой, называются играми с ненулевой суммой [19].

В зависимости от числа возможных стратегий игры делятся на конечные и бесконечные. Игра называется конечной, если у каждого игрока имеется только конечное число стратегий. Игра называется бесконечной, если хотя бы у одного игрока имеется бесконечное число стратегий [19].

По количеству ходов, которые делают игроки для достижения своих целей, игры бывают одношаговые и многошаговые. Одношаговые игры заключаются в том, что игрок выбирает одну из доступных ему стратегий и делает всего один-единственный ход. В многошаговых играх игроки для достижения своих целей делают последовательно ряд ходов, которые могут ограничиваться правилами игры либо могут продолжаться до тех пор, пока у одного из игроков не останется ресурсов для продолжения игры [19].

В последнее время получили большое распространение так называемые деловые игры. Деловая игра имитирует взаимодействие людей и проявляется как упражнение в последовательном принятии множества решений, основанное на некоторой модели коммерческой деятельности и на исполнении участниками игры конкретных ролей-должностей. Деловые игры предназначены для воспроизведения и согласования коммерческих интересов. В основе конструкции игры лежат взаимосвязь ресурсов и использование знаний об их возможностях. Деловые игры имитируют организационно-экономические взаимодействия в различных звеньях коммерческих организаций и предприятий [19].

Основными вопросами теории игр, которые возникают в коммерческой деятельности, являются:

1) в чем состоит оптимальность поведения каждого из игроков в игре, какие свойства стратегий следует считать признаками оптимальности;

2) существуют ли стратегии игроков, которые обладали бы атрибутами оптимальности;

3) если существуют оптимальные стратегии, то как их найти? [19]

Постановка игровых задач

Решения, принимаемые в управленческой деятельности, связаны обычно с распределением ресурсов организации: товаров, денег, людей, оборудования и т.д., выбором наиболее выгодных проектов.

Рассмотрим теорию игр на примере коммерческой организации. Организация представляет собой систему взаимодействующих, взаимозависимых или подчиненных подразделений: дирекция и некоторое количество производственных единиц. Целью коммерческой организации является максимизация доходов или минимизация затрат.

Пусть n – число отделов,

m – число различных ресурсов,

x_i – i-ый вариант выполнения товарооборота, i – номер отдела, ,

y_j – j-ый вид ресурса, выделяемый коммерческим директором, ,

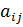- исход, получаемый при стратегии x_i и состоянии среды y_j, ,

Y – суммарный объем ресурсов, которыми распоряжается коммерческий директор,

С – доход или потери, связанные с реализацией товара.

В терминах игровой модели можно дать следующую интерпретацию:

n – число стратегий отдела,

m – число состояний среды,

x_i – i-ая стратегия, ,

y_j – j-ое состояние среды, ,

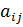- исход, получаемый при стратегии x_i и состоянии среды y_j, , .

Математическая модель сформулированной задачи имеет вид:

Максимизировать (минимизировать) величину , ,…,

при ограничениях .

Продажа товаров коммерческим предприятием может быть описана соотношением

где – фактор, значение которого хорошо известно руководству i-го товарного отдела, но руководство коммерческого предприятия достаточной информации о нем не имеет.

Это может быть отбраковка товаров, колебания спроса, неравномерность потока покупателей и т.д. Таким образом, выделенный ресурс у _j и выбранная технология работы товарного отдела х _i не дают руководству коммерческого предприятия полной информации о том, какая будет реализована продукция 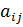- это знает только i-й отдел. Очевидно, что существует зависимость , в которой есть неопределенные факторы , конкретные значения которых в момент распределения ресурсов у _j между товарными отделами неизвестны руководству коммерческого предприятия. В этих случаях разумно воспользоваться принципом гарантированного результата, т. е. поставить задачу: найти такое распределение ресурса у _j чтобы при этом достигался

следовательно, руководство магазина так распределяет ресурсы, чтобы минимизировать потери при наихудшем возможном значении неопределенного фактора или

следовательно, руководство коммерческого предприятия так распределяет ресурсы между товарным отделом, чтобы максимизировать доходы при наихудшем возможном значении неопределенного фактора.

Пример. Рассмотрим постановку и решение следующей задачи. Сеть продуктовых магазинов заключила договор на централизованную поставку овощей из теплиц на сумму 10 000 руб. ежедневно. Если в течение дня овощи не поступают, сеть магазинов имеет убытки в размере 20 000 руб. от невыполнения плана товарооборота. Сеть магазинов может осуществить самовывоз овощей фермера. Для этого она может сделать заказ в транспортной организации, что вызовет дополнительные расходы в размере 500 руб. Однако опыт показывает, что в половине случаев посланные машины возвращаются без овощей. Можно увеличить вероятность получения овощей от фермера до 80 %, если предварительно посылать туда своего представителя, что требует дополнительных расходов в размере 400 руб. Существует возможность заказать дневную норму овощей у другого надежного поставщика – плодоовощной базы по повышенной на 50 % цене. Однако в этом случае, кроме расходов на транспорт (500 руб.), возможны дополнительные издержки в размере 300 руб., связанные с трудностями реализации товара, если в тот же день поступит и централизованная поставка от фермера. Какой стратегии надлежит придерживаться магазину, если заранее неизвестно, поступит или не поступит централизованная поставка.

Построим игровую модель этой задачи. Игроками являются представители сети магазинов и поставщика. Перечислим стратегии первого игрока – поставщика.

П₁ – поставка своевременная,

П₂ – поставки нет.

У сети магазинов имеются четыре стратегии поведения:

M₁ – ожидать поставку, не принимая дополнительных мер;

М₂ – послать к поставщику свой транспорт;

М₃ – послать к поставщику представителя и транспорт;

М₄ – заказать поставку у плодоовощной базы.

Всего возможны 8 совместных ситуаций, которые запишем в таблицу.

Ситуации	Стоимость овощей	Убытки от непоставки	Транспортные расходы	Командировочные расходы	Издержки от реализации	Всего за день
М₁П₁	10000	0	0	0	0	10000
М₁П₂	0	20000	0	0	0	20000
М₂П₁	10000	0	500	0	0	10500
М₂П₂	5000	10000	500	0	0	15500
М₃П₁	10000	0	500	400	0	10900
М₃П₂	8000	4000	500	400	0	12900
М₄П₁	25000	0	500	0	300	25800
М₄П₂	15000	0	500	0	0	15500

Для того чтобы легче было разобраться в сложившихся ситуациях и по возможности оценить их, составим платежную матрицу. Число столбцов равно числу стратегий первого – поставщика, число строк равно числу стратегий второго игрока – сети магазинов.

Платежная матрица

Стратегия сети магазинов	Стратегия поставщика
Стратегия сети магазинов	П₁	П₂
М₁	-10000	-20000
М₂	-10500	-15500
М₃	-10900	-12900
М₄	-25800	-15500

Выбор стратегии сети магазинов зависит от надежности поставщика продукции, которую можно оценить величиной вероятности p ₁, следовательно, p ₂ =1- p ₁ – величина ненадежности поставщика. По платежной матрице составим уравнения затрат сети магазинов Е от надежности поставщика для каждой стратегии сети магазинов:

М₁: Е( p ₁ )=10000 p ₁ +20000(1- p ₁ )

М₂: Е( p ₁ )=10500 p ₁ +15500(1- p ₁ )

М₃: Е( p ₁ )=10900 p ₁ +12900(1- p ₁ )

М₄: Е( p ₁ )=25800 p ₁ +15500(1- p ₁ )

Если своевременная поставка осуществляется с вероятностью 0,4, тогда ожидаемые затраты сети магазинов составят соответственно:

М₁: Е(0,4)=10000 ×0,4+20000(1- 0,4)=16000

М₂: Е(0,4)=10500 ×0,4+15500(1- 0,4)=13500

М₃: Е(0,4)=10900 ×0,4+12900(1- 0,4)=12100

М₄: Е(0,4)=25800 ×0,4+15500(1- 0,4)=19620

Таким образом, минимальные расходы магазин понесет в том случае, если примет стратегию М₃, т. е. не только пошлет фермеру автотранспорт, но и отправит туда своего представителя.

Методы и модели решения игровых задач. Принцип минимакса (осторожности)

Рассмотрим конечную парную игру с нулевой суммой. Игрок I имеет m альтернатив (А₁, A₂, ..., А _m,) а игрок II - n стратегий (B ₁ , B ₂ ,… B_n). Такая игра называется игрой размерностью m × n. Пусть каждая сторона выбрала определенную стратегию: игрок I – А _i (i= 1, 2, ...,m), игрок II – B_j (j= 1, 2, ...,n). Если такая таблица составлена, то игра приведена к матричной форме и называется матричной игрой.

Пусть a_ij – выигрыш игрока I в ситуации, когда игрок выбрал стратегию А _i, а игрок II выбрал стратегию B_j. Выигрыш игрока II в данной ситуации обозначим через b _ij.

Рассматриваем игру с нулевой суммой, следовательно, a_ij = - b _ij для любых i и j и для проведения анализа достаточно знать выигрыш только одного из игроков. Если игра состоит только из личных ходов, то выбор стратегии (А _i, B_j) однозначно определяет исход игры, например, выигрыш игрока I. Если игра содержит также случайные ходы, то выигрыш при паре стратегий (А _i, B_j) есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае ожидаемый выигрыш – это среднее значение (математическое ожидание). Предположим, что значения a_ij известны для каждой пары стратегий (А _i, B_j). Составим таблицу, строки которой соответствуют стратегиям игрока I, а столбцы – стратегиям игрока II. Такая таблица называется платежной матрицей. Каждый элемент ( a_ij > 0) матрицы определяет величину выигрыша игрока I и проигрыш игрока II при применении соответствующих стратегий (А _i, B_j). Цель игрока I – максимизировать свой выигрыш, а игрока II – минимизировать свой проигрыш.

Будем считать, что все a_ij > 0. Этого всегда можно добиться прибавлением достаточно большого положительного числа ко всем строкам и столбцам матрицы. Такое изменение матрицы не повлияет на результат. Таким образом, платежная матрица имеет вид:

I / II	B₁	B₂	…	B_j	…	B_n
A₁	a₁₁	a₁₂	…	a_1j	…	a_1n
A₂	a₂₁	a₂₂	…	a_2j	…	a_2n
…	…	…	…	…	…	…	…
A_i	a_i1	a_i2	…	a_ij	…	a_in
…	…	…	…	…	…	…	…
A_m	a_m1	a_m2	…	a_mj	…	a_mn

Задача состоит в определении:

1) наилучшей (оптимальной) стратегии игрока I из стратегий (А₁, A₂, ..., А _m,),

2) наилучшей (оптимальной) стратегии игрока II из стратегий (B ₁ , B ₂ ,… B_n).

Для решения задачи применяется принцип, согласно которому участники игры разумны и каждый из них делает все для того, чтобы добиться своей цели – выиграть.

Проанализируем последовательно каждую стратегию игрока I. Если игрок I выбирает стратегию А₁, то игрок II может выбрать такую стратегию B_j, при которой выигрыш игрока I будет равен наименьшему из чисел a_ij:

то есть – минимальное значение из всех чисел первой строки. Тогда по аналогии выражение для любой стратегии А_i будет иметь вид:

Выбирая стратегию А_i, игрок I должен рассчитывать на то, что в результате разумных действий игрока II он не выиграет больше, чем . Поэтому игрок I должен выбрать ту стратегию, для которой это число – максимально

то есть - максимальное значение из всех чисел столбца :

Величина – гарантированный выигрыш, который может обеспечить себе игрок I при любом поведении игрока II. Величина называется нижней ценой игры, или максимином, а стратегия А_i, игрока I, обеспечивающая получение нижней цены игры, называется максиминной чистой перестраховочной стратегией, при этом игрок I при любом поведении игрока II обеспечивает себе выигрыш не меньше .

Игрок II заинтересован в том, чтобы уменьшить свой проигрыш, то есть обратить выигрыш игрока I в минимум. Для выбора оптимальной стратегии он должен найти максимальное значение выигрыша в каждом столбце и среди этих значений выбрать наименьшее. Обозначим через максимальное значение в каждом столбце:

Наименьшее значение обозначим через β:

То есть

называется верхней ценой игры, или минимаксом. Стратегия игрока II, обеспечивающая получение верхней цены игры, называется минимаксной чистой стратегией. Применяя ее, игрок II проиграет не больше при любых действиях игрока I.

Принцип, диктующий игрокам выбор соответствующих стратегий (максиминной и минимаксной), в теории игр называется принципом минимакса - принцип гарантированного результата. Этот принцип был впервые сформулирован Дж. фон Нейманом в 1928 г.

Существуют матричные игры, для которых нижняя цена игры равна верхней, т.е. = . Такие игры называются играми с седловой точкой, в этом случае = называется чистой ценой игры, а стратегии игроков А_i*, и В_j*, позволяющие достичь этого значения, - оптимальными. Пара (А_i*, В_j*) называется седловой точкой матрицы, так как элемент 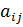= одновременно является минимальным в i-ой строке и максимальным в j-м столбце. Оптимальные стратегии А_i* и В_j* и чистая цена являются решением игры в чистых стратегиях, т. е. без привлечения механизма случайного выбора.

При постановке задач необходимо иметь в виду некоторые преобразования, которые помогают упростить сложную задачу путем изменения — уменьшения размерности платежной матрицы посредством выделения и исключения доминирующих и дублирующих стратегий.

Пример. С учетом вариантов конъюнктуры B₁, В₂, В3, В₄, В₅, сложившейся на рынке, и поведения покупателей в микрорайоне города коммерческое предприятие разработало шесть технологий продажи товаров A₁, А₂, A₃, А₄, А₅, А₆. Упростить платежную матрицу. Возможные варианты среднедневного товарооборота в млн. руб. приведены в таблице.

I / II	В₁	В₂	В₃	В₄	В₅
А₁	0,4	0,9	0,5	0,5	0,6
А₂	0,6	0,5	0,7	0,8	0,9
А₃	0,6	0,3	0,8	0,6	0,7
А₄	0,3	0,8	0,5	0,4	0,3
А₅	0,1	0,3	0,5	0,4	0,3
А₆	0,4	0,8	0,5	0,4	0,5

Стратегия A₁ доминирует над стратегией А₆, а стратегия А₄ доминирует над стратегией А₅, следовательно, исключаем 5-ую и 6-ую строки матрицы.

I / II	В₁	В₂	В₃	В₄	В₅
А₁	0,4	0,9	0,5	0,5	0,6
А₂	0,6	0,5	0,7	0,8	0,9
А₃	0,6	0,3	0,8	0,6	0,7
А₄	0,3	0,8	0,5	0,4	0,3

С позиций проигрышей игрока В стратегии В₃, В₄ и В₅ доминируют над стратегией B₁, поэтому эти столбцы исключаем

I / II	В₁	В₂
А₁	0,4	0,9
А₂	0,6	0,5
А₃	0,6	0,3
А₄	0,3	0,8

С позиций игрока А стратегия А₁доминирует над стратегией A₄, а стратегия А₂ доминирует над стратегией A₃, поэтому исключим 3-ю и 4-ю строки и в результате получаем сокращенную матрицу:

I / II	В₁	В₂
А₁	0,4	0,9
А₂	0,6	0,5

Пример. Дана платежная матрица. Найти решение игры, т. е. определить нижнюю и верхнюю цены игры и минимаксные стратегии.

I / II	В₁	В₂	В₃	В₄
А₁	5	3	8	2
А₂	1	6	4	3
А₃	9	5	4	7

Таким образом, нижней цене игры (α = 4) соответствует стратегия А₃ игрока I. Выбирая эту стратегию, игрок I достигнет выигрыша не меньше 4 при любом поведении игрока II. Верхней цене игры (β = 6) соответствует стратегия игрока II – В₂. Эти стратегии являются минимаксными. Если обе стороны будут придерживаться этих стратегий, выигрыш будет равен 5 (а₃₃).

Игровые модели в условиях коммерческого риска

Риск определяется возможностью отклонения от желаемого результата в худшую сторону или выхода за пределы допустимого диапазона, что приводит к негативным последствиям.

Для принятия решений в условиях риска используют методы теории вероятностей, если это возможно. В таком случае факторы, например, состояния среды, представляют собой либо случайные величины, либо случайные функции. Они описываются какими-либо статистическими характеристиками, например, математическим ожиданием и дисперсией, и обладают статистической устойчивостью. Принимающий решение ориентируется на средние, наиболее вероятные результаты, например, дохода, однако при этом не исключен риск получения не того результата, на который была рассчитана коммерческая стратегия, тогда мерой риска следует считать среднее квадратическое отклонение.

Ситуации, в которых риск связан не с сознательным противодействием противоположной стороны (среды), а с недостаточной осведомленностью о ее поведении или состоянии лица, принимающего решение, называются «играми с природой».

В таких играх человек старается действовать осмотрительно, например, используя стратегию, позволяющую получить наименьший проигрыш. Второй игрок (природа) действует незлонамеренно, совершенно случайно, возможные стратегии его известны (стратегии природы). Такие ситуации исследуются с помощью теории статистических решений. Рассмотрим «игру с природой» в условиях частичной неопределенности. Пусть у игрока I имеется т возможных стратегий A₁, А₂, ..., А_m и можно сделать n предположений о состояниях природы (среды) П₁, П₂,..., П_n с известными вероятностями их появления p_j.. Пусть известен выигрыш а _ij , , который получает игрок I при выборе стратегии А_i для каждого состояния природы П_j. Тогда можно составить платежную матрицу А следующего вида:

I/II	П₁	П₂	…	П_j	…	П_n
А₁	a₁₁	a₁₂	…	a_1j	…	a_1n
А₂	a₂₁	a₂₂	…	a_2j	…	a_2n
…
А_i	a_i1	a_i2	…	a_ij	…	a_in
…
А_m	a_m1	a_m2	…	a_mj	…	a_mn

Для каждой стратегии А_i можно рассчитать величину математического ожидания выигрыша:

Оптимальной будет считаться та стратегия, для которой эта величина принимает максимальное значение

При этом следует заметить, что оптимизация в среднем не исключает полностью влияние фактора случайности.

Пример. Для доставки свежих фруктов из Краснодара в Москву можно использовать три вида транспорта: Т₁ – воздушный, Т₂ – автомобильный, Т₃ – железнодорожный. Ожидаемые величины дохода 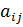с учетом затрат на транспортировку, погрузочно-разгрузочные работы и сроков доставки фруктов и потерь и вместе с условными вероятностями их получения 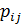представлены в таблице:

	a_i1	p_i1	a_i2	p_i2	a_i3	p_i3
Т₁	300	0,6	200	0,3	-300	0,1
Т₂	450	0,2	300	0,8	-200	0,1
Т₃	600	0,1	450	0,7	-100	0,1
β_j	600		450		-100

Для выбора наиболее оптимального варианта доставки свежих фруктов сначала находим для каждого вида транспорта математическое ожидание выигрыша:

М(Т₁)=300×0,6+200×0,3+(-300) ×0,1=210,

М(Т₂)=450×0,2+300×0,7+(-200) ×0,1=280,

М(Т₃)=600×0,1+450×0,8+(-100) ×0,1=410,

а затем определяем максимальное значение этого показателя, которое и указывает на оптимальное решение:

следовательно, наиболее выгодно доставлять свежие фрукты в Москву из Краснодара железнодорожным транспортом.

При исследовании «игры с природой» вводится показатель, позволяющий оценить, насколько то или иное состояние «природы» влияет на исход. Этот показатель называется риском. При пользовании стратегией А_i и состоянием среды П_j разность между максимально возможным выигрышем β_j при данном состоянии «природы» П_j и выигрышем a_ij при выбранной стратегии А_i называется риском r_ij:

где

т. е. максимальное число в столбце состояния среды П_j, .

Построим матрицу рисков для нашего примера:


Т₁	300	0,6	250	0,3	200	0,1	275
Т₂	150	0,2	150	0,7	100	0,1	145
Т₃	0	0,1	0	0,8	0	0,1	0

Для решения задачи можно пользоваться значениями среднего риска:

Оптимальным в этом случае будет та стратегия, для которой средний риск будет минимальным

Отсюда находим средний риск для каждой стратегии:

=300×0,6+250×0,3+200×0,1=275,

=150×0,2+150×0,7+100×0,1=145,

=0×0,1+0×0,8+0×0,1=0,

отсюда следует, что минимальный риск соответствует стратегии Т₃, то есть целесообразно доставлять свежие фрукты железнодорожным транспортом.

Игровые модели конфликтов

Теория игр представляет собой набор математических инструментов для построения моделей, а в социально-экономических приложениях является неиссякаемым источником гибких концепций. Игра является математической моделью коллективного поведения, отображающей взаимодействие участников-игроков в стремлении добиться лучшего исхода, причем их интересы могут быть различны. Несовпадение, антагонизм интересов порождают конфликт, а совпадение интересов приводит к кооперации.

Часто интересы в социально-экономических ситуациях не являются ни строго антагонистическими, ни точно совпадающими. Продавец и покупатель согласны, что в их общих интересах договориться о продаже, конечно, при условии, что сделка выгодна обоим. Однако они энергично торгуются при выборе конкретной цены в пределах, определяющихся условиями взаимной выгоды. Теория игр позволяет выработать оптимальные правила поведения в конфликтах. Возможность конфликтов заложена в существе самой человеческой жизни.

Причины конфликтов коренятся в аномалиях общественной жизни и несовершенстве самого человека. Среди причин, порождающих конфликты, следует назвать прежде всего социально-экономические, политические и нравственные причины. Они являются питательной средой для возникновения различного рода конфликтов. На возникновение конфликтов оказывают влияние психофизические и биологические особенности людей.

Во всех сферах человеческой деятельности при решении самых разнообразных задач в быту, на работе или отдыхе приходится наблюдать различные по своему содержанию и силе проявления конфликты. Об этом ежедневно пишут газеты, передают по радио, транслирует телевидение. Они занимают значительное место в жизни каждого человека, причем последствия некоторых конфликтов бывают слишком ощутимы даже на протяжении многих лет жизни.

Они могут съедать жизненную энергию одного человека или группы людей в течение нескольких дней, недель, месяцев или даже лет. Бывает так, правда редко, к сожалению, что разрешение одних конфликтов проходит весьма корректно и профессионально грамотно, а других, что бывает значительно чаще, непрофессионально, безграмотно, с плохими исходами иногда для всех участников конфликта, где нет победителей, а есть только побежденные. Очевидно, необходимы рекомендации по рациональному образу действий в конфликтных ситуациях. Причем чаще часть конфликтов являются надуманными, искусственно раздутыми, созданными для прикрытия профессиональной некомпетентности некоторыми лицами и вредны в коммерческой деятельности.

Другие же конфликты, являясь неизбежным спутником жизни любого коллектива, могут быть весьма полезны и служат импульсом для развития коммерческой деятельности в лучшую сторону. Конфликты в настоящее время являются ключевой проблемой жизни как отдельных личностей, так и целых коллективов. Действия литературных персонажей, героев неизбежно сопровождаются проявлением, развитием какого-либо жизненного конфликта, который так или иначе разрешается иногда мирно, иногда драматически или трагически, например, на дуэли.

Лучшими источниками наших знаний о человеческих конфликтах являются классические трагедии, серьезные и глубокие романы, их экранизация или театральная постановка. Деятельности человека могут противостоять в конфликте интересы других людей или стихийные силы природы. В одних конфликтах противоположной стороной выступает сознательно и целенаправленно действующий активный противник, заинтересованный в нашем поражении, сознательно препятствует успеху, старается сделать все от него зависящее, чтобы добиться своей победы любыми средствами, например, с помощью киллера.

В других конфликтах такого сознательного противника нет, а действуют лишь «слепые силы природы»: погодные условия, состояние торгового оборудования на предприятии, болезни сотрудников и т.п. В таких случаях природа не злонамеренна и выступает пассивно, причем иногда во вред человеку, а иногда к его выгоде, однако ее состояние и проявление могут ощутимо влиять на результат коммерческой деятельности. Движущей силой в конфликте является любопытство человека, стремление победить, сохранить или улучшить свое положение, например, безопасность, устойчивость в коллективе или надежда на успех достижения поставленной в явном или неявном виде цели. Как поступить в той или иной ситуации, часто бывает неясно.

Характерной особенностью любого конфликта является то, что ни одна из участвующих сторон не знает заранее точно и полностью всех своих возможных решений, а также и другие стороны, их будущее поведение и, следовательно, каждый вынужден действовать в условиях неопределенности. Неопределенность исхода может быть обусловлена как сознательными действиями активных противников, так и несознательными, пассивными проявлениями, например, стихийных сил природы: дождя, солнца, ветра, лавины и т.п.

В таких случаях исключается возможность точного предсказания исхода. Общность всех конфликтов независимо от их природы заключается в столкновении интересов, стремлений, целей, путей достижения целей, отсутствия согласия двух или более сторон — участников конфликта. Сложность конфликтов обусловливается разумными и расчетливыми действиями отдельных лиц или коллективов с различными интересами.

Неопределенность исхода конфликта, любопытство, интерес и стремление к победе побуждают людей к сознательному вступлению в конфликт, что притягивает к конфликтам и участников, и наблюдателей. Математическая теория игр дает научно обоснованные рекомендации поведения в конфликтных ситуациях, показывая «как играть, чтобы не проиграть». Для применения этой теории необходимо уметь представлять конфликты в виде игр. Основой любого конфликта является наличие противоречия, которое принимает форму разногласий.

Конфликт можно определить, как отсутствие согласия между двумя или более сторонами – лицами или группами, проявляющееся при попытке разрешить противоречие, причем часто на фоне острых отрицательных эмоциональных переживаний, хотя известно, что из двух ссорящихся виновный тот, кто умнее. Следует заметить, что вовлечение в конфликт в коммерческой деятельности большого количества людей позволяет резко увеличить и обнаружить множество альтернатив и исходов, что является важной позитивной функцией конфликта, связанной с расширением кругозора, увеличением количества альтернатив и соответственно возможных исходов.

В процессе коммерческих переговоров приходится искать область взаимных интересов (рис. 2.1), позволяющую найти компромиссное решение.

Рис. 2.1. Область вариантов компромиссных решений на переговорах

Делая большие уступки по менее значимым аспектам для фирмы, но более значимым для оппонента, коммерсант получает больше по другим позициям, которые более значимы и выгодны для фирмы. Эти уступки имеют минимальные и максимальные границы интересов. Это условие получило название «принцип Парето» по имени итальянского ученого В. Парето. Одним из типичных социально-психологических межличностных конфликтов является несбалансированное ролевое взаимодействие. Теоретическую основу анализа межличностных конфликтов предложил американский психолог Э. Берн, который дал описание взаимодействия партнеров (рис. 2.2) в виде сетевых моделей.

Рис. 2.2. Сетевые модели ролевого взаимодействия партнеров

Каждый человек в процессе взаимодействия с окружающими вынужден играть более десятка ролей, причем далеко не всегда успешно. В предлагаемой модели каждый партнер может имитировать роль С — старшего, Р — равного или М — младшего. Если ролевое взаимодействие сбалансировано, то общение может развиваться бесконфликтно, иначе при разбалансе ролей возможен конфликт. В длительных конфликтах часто доля делового содержания с течением времени уменьшается и начинает доминировать личностная сфера, что и представлено на рис. 2.3

Рис. 2.3. Изменение соотношения деловой и личностной составляющих сфер конфликта

Конфликт представляет собой процесс, развивающийся во времени (рис. 2.4), который можно разделить на несколько периодов. Таковыми, например, могут быть предконфликтный период (t_n), конфликтное взаимодействие (t_k) и послеконфликтный период (t_c). Напряженность с течением времени в предконфликтный период (t ₀ - t ₁) постепенно (1) или лавинообразно (2) нарастает, а затем достигает наибольшего значения в момент кульминации t ₂ и затем спадает. Следует заметить, что зачастую конфликтное взаимодействие имеет продолжительность (t ₃ - t ₁) всего около 1 мин., а послеконфликтный период может быть больше его в 600-2000 и более раз. Причем показатели исхода конфликта для обеих сторон могут совсем не содержать выигрышных показателей, т. е. одни ущербы.

Рис. 2.4. Динамические модели развития конфликтов

Состояние человека во взаимодействии можно интерпретировать графически в виде сочетания степени его активности А и уровня настроения (рис. 2.5).

Рис. 2.5. Графическая модель оценки состояния партнера

Измерение этих показателей можно производить от среднего, нейтрального (0) уровня. Тогда точка состояния определяется вектором с соответствующими координатами, например M(x₁, y₂). Состояние, определяемое другим вектором N(x₁,y₁), отличается меньшей активностью у = (у₂ – у₁). Состояние партнера, определяемое вектором А(х₃, у₂), отличается более скверным настроением, чем состояние, определяемое вектором В(х₂, у₂). На рис. 2.6 представлена модель взаимодействия партнеров, состояния которых зафиксированы векторами А и В, по которым можно построить результирующий конфликт-вектор Е. Эта зона готовности к конфликту из всех квадрантов является самой неблагоприятной. Пользуясь такими графическими моделями оценки состояния партнеров, можно заранее подготовиться к возможным исходам их взаимодействия.

Рис. 2.6. Модель взаимодействия партнеров

Игровую модель конфликта можно представить как сочетание отображения (рис. 2.7) возможных позитивных и негативных альтернатив (ходов) участников-игроков К и П и вариантов исходов для каждой пары ходов К, П в виде платежной матрицы В = ||b_ij||, элемент которой можно определить по формуле

где и – соответственно оценка характеристики исхода конфликта в баллах и ее вес, .

На рис. 2.7 показано, что действия обеих сторон негативными альтернативами (-/-) свидетельствуют о том, что с помощью «войн» понять друг друга нельзя. Позитивные действия с обеих сторон приводят к мирному исходу. Варианты альтернатив (-/+) или (+/-) могут привести к мирному варианту согласия, что определяется цепочкой причинно-следственных альтернатив в многоходовом взаимодействии.

Рис. 2.7. . Игровая модель конфликта

Пример. Рассмотрим пример решения конфликтной ситуации.

Рынок. Женщина заплатила за 2кг помидоров, а контрольные весы показали недовес 200 г. Она попросила продавца забрать помидоры и вернуть деньги. Продавец отказал и оскорбил покупательницу Альтернативы покупательницы: П₁ – вызвать администрацию, П₂ ~ обратиться в правоохранительные органы, П₃ – оскорбить продавца и потребовать вернуть деньги.

Альтернативы продавца: K₁ – вернуть деньги, К₂ – оскорбить покупательницу и не вернуть деньги, К₃ – не вернуть деньги.

В качестве характеристик оценки исходов конфликта выберем следующие.

1. Э – сила эмоционального возбуждения, дб. (0,19);

2. t _k – время конфликтного взаимодействия, мин. (0,17);

3. τ - продолжительность негативных эмоций, мин. (0,15);

4. О_с – количество обидных, грубых слов, шт. (0,13);

5. Л_k – количество участников конфликта, чел. (0,11);

6. t_сп – послеконфликтный период, мин (0,09);

7. Т – суммарные затраты времени, мин. (0,07);

8. З_М – затраты материальные, руб. (0,05);

9. t _n – предконфликтный период, мин. (0,03);

10. τ₊ - продолжительность позитивных и нейтральных эмоций, мин. (0,01).

Характеристики расположены по рангу, в скобках указан их вес М_k, найденный методом парных сравнений.

Введем 10-балльную оценку характеристик конфликта по шкале хуже (Б_k= 1) – лучше (Б_k = 10) и сформируем матрицу их возможных значений в таблице.

Б_k P_ij	1	2	3	4	5	6	7	8	9	10
Э	9	8	7	6	5	4	3	2	1	0
t _k	10	8	7	9	5	4	3	2	1	0
τ	400	300	200	160	100	80	60	40	20	0
О_с	10	9	8	7	6	5	4	3	2	0
Л_k	10	9	8	7	6	5	4	3	2	0
t_сп	400	300	200	150	100	80	60	40	20	0
Т	410	310	210	160	110	90	70	50	30	0
З_М	1500	1000	500	300	200	100	60	30	6	0
t _n	30	25	20	15	10	8	6	4	2	0
τ₊	0	1	2	3	4	5	6	7	8	∞

Теперь необходимо для каждой пары альтернатив (П_i, К_j) установить фактические значения характеристик конфликта Р_ij, определить балльную оценку характеристик Б_k(Р_ij), а затем вычислить значения исходов b_ij по формуле

где m – количество характеристик конфликта;

– вес k-ой характеристики конфликта;

– балльное значение k-ой характеристики конфликта исхода пары альтернатив Р _i , K_j.

Например, для пары альтернатив П₁, K₁ и условных значениях характеристик найдем значение исхода b_ij:

b₁₁ = 0,19 × 5 + 0,17 ×.1 + 0,15 × 3 + 0,13 × 1 + 0,11 × 5 + 0,09 × 3 + + 0,07 × × 3 + 0,05 × 9 + 0,03 × 9 + 0,01 × 1 = 3,23.

Аналогично проводим вычисления исходов для остальных пар альтернатив и таким образом построим игровую модель конфликтной ситуации в виде платежной матрицы:

Пользуясь принципом минимакса, находим нижнюю и верхнюю цены игры, которые равны α = β = 3,23, тогда пара альтернатив П₁, K₁ определяют седловую точку игры. Следовательно, минимаксные стратегии участников конфликта П₁ и K₁ являются оптимальными.

Фактически покупательница так и сделала: вызвала администратора, который изъял гири у продавца, запретил торговлю, а продавец принял назад помидоры и вернул деньги. Следует заметить, что при других значениях показателей конфликта может быть построена матрица, которая не содержит седловой точки, тогда можно пользоваться критериями Вальда, Сэвиджа, Гурвица, а также воспользоваться симплексным методом линейного программирования для решения игры в смешанных стратегиях.

Практическое занятие 11

1. Дана платежная матрица. Определите оптимальные стратегии игроков, верхнюю и нижнюю цену игры.

I II	В₁	В₂	В₃	В₄	В₅	В₆
А₁	20	40	50	70	10	30
А₂	15	25	70	50	20	10
А₃	80	35	40	80	90	25
А₄	45	70	90	70	25	55

2. Определите оптимальную стратегию в «игре с природой», заданной следующей платежной матрицей:

I II	П₁	р_i₁	П₂	р_i₂	П₃	р_i3	П₄	р_i₄
А₁	20	0,15	40	0,25	50	0,3	70	0,25
А₂	15	0,35	25	0,15	70	0,25	50	0,25
А₃	80	0,3	35	0,4	40	0,35	80	0,4
А₄	45	0,2	70	0,2	90	0,1	70	0,1

Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.

3. Определите оптимальную стратегию в «игре с природой», заданной платежной матрицей. Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.

I II	П₁	р_i₁	П₂	р_i₂	П₃	р_i3	П₄	р_i₄
А₁	10	0,1	15	0,15	25	0,25	20	0,2
А₂	20	0,15	25	0,1	35	0,1	10	0,3
А₃	15	0,25	10	0,2	20	0,15	30	0,1
А₄	25	0,2	40	0,3	30	0,1	40	0,1
А₅	40	0,2	35	0,15	55	0,15	60	0,1
А₆	30	0,1	20	0,1	10	0,25	50	0,2

4. Определите оптимальную стратегию в «игре с природой», заданной платежной матрицей. Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.

I II	П₁	р_i₁	П₂	р_i₂	П₃	р_i3	П₄	р_i₄	П₅	р_i₅
А₁	25	0,2	55	0,2	35	0,35	60	0,25	25	0,35
А₂	35	0,25	60	0,1	25	0,15	50	0,25	35	0,15
А₃	20	0,1	45	0,35	20	0,15	40	0,2	45	0,1
А₄	40	0,35	70	0,15	40	0,15	50	0,2	65	0,25
А₅	45	0,1	30	0,2	30	0,2	30	0,1	25	0,15

5. Перед администрацией муниципального образования стоит задача по ремонту дорог в трех микрорайонах города. На выполнение работ претендуют 4 компании. По предыдущим результатам сотрудничества имеются следующие данные: первая компания может превысить запланированную стоимость работ на 15 % в каждом микрорайоне с вероятностью 10 %, 11 %, 9 % соответственно; вторая компания может превысить запланированную стоимость работ на 14 % в каждом микрорайоне с вероятностью 15 %, 10 %, 12 % соответственно; третья компания может превысить запланированную стоимость работ на 16 % в каждом микрорайоне с вероятностью 9 %, 8 %, 10 % соответственно; четвертая компания может превысить запланированную стоимость работ на 13 % в каждом микрорайоне с вероятностью 11 %, 12 %, 14 % соответственно. Выбрать наиболее надежную фирму для выполнения ремонтных работ в рамках заложенной в бюджет стоимости, если для ремонта дорог в первом микрорайоне запланировано 3 млн. руб., второго – 3,5 млн. руб., третьего – 2,8 млн. руб.

6. Перед администрацией муниципального образования стоит задача строительства школ в пяти микрорайонах города. На выполнение работ претендуют 3 компании. По предыдущим результатам сотрудничества имеются следующие данные: первая компания может превысить запланированную стоимость работ на 20 % в каждом микрорайоне с вероятностью 12 %, 13 %, 10 % соответственно; вторая компания может превысить запланированную стоимость работ на 18 % в каждом микрорайоне с вероятностью 14 %, 15 %, 13 % соответственно; третья компания может превысить запланированную стоимость работ на 16 % в каждом микрорайоне с вероятностью 21 %, 19 %, 22 % соответственно. Выбрать наиболее надежную фирму для строительства школ в рамках заложенной в бюджет стоимости, если для строительства школ в первом микрорайоне запланировано 230 млн. руб., второго – 350 млн. руб., третьего – 310 млн. руб.

Домашнее задание:

1. Определите минимаксные стратегии игроков (нижнюю и верхнюю цены игры).

I II	В₁	В₂	В₃	В₄	В₅
А₁	5	8	7	6	3
А₂	10	12	4	7	2
А₃	15	10	8	7	4
А₄	10	7	8	12	6
А₅	7	10	11	3	5
А₆	7	2	3	12	4

2. Определите оптимальную стратегию в «игре с природой», заданной платежной матрицей. Составьте матрицу рисков и определите оптимальную стратегию по критерию минимального риска.

I II	П₁	р_i₁	П₂	р_i₂	П₃	р_i₃	П₄	р_i₄
А₁	25	0,1	15	0,15	15	0,25	45	0,2
А₂	35	0,15	20	0,1	25	0,1	55	0,3
А₃	60	0,25	25	0,2	35	0,15	25	0,1
А₄	45	0,2	35	0,3	15	0,1	35	0,1
А₅	70	0,2	45	0,15	45	0,15	65	0,1
А₆	50	0,1	20	0,1	65	0,25	70	0,2

3. Сформулировать и решить задачу для нахождения минимаксных стратегий, нижней и верхней цен игры.

4. Сформулировать и решить задачу игры с «природой».

Дата: 2019-05-28, просмотров: 286.

⇐ Предыдущая 6 7 8 9 10 11 121314 15 Следующая ⇒