Интегрирование методом подстановки.

Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла.

Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.

Пример.

Найти неопределенный интеграл .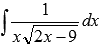

Решение.

Введем новую переменную 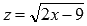. Выразим х через z:

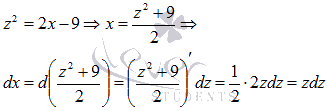
Выполняем подстановку полученных выражений в исходный интеграл:

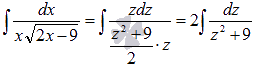
Из таблицы первообразных имеем .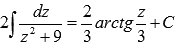

Осталось вернуться к исходной переменной х:

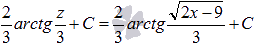
Ответ:

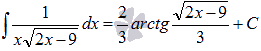
При интегрировании функций с иррациональностью вида 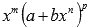, где m, n, p – рациональные числа, важно правильно выбрать выражение для введения новой переменной. Смотрите рекомендации в разделе интегрирование иррациональных функций.

Очень часто метод подстановки используется при интегрировании тригонометрических функций. К примеру, использование универсальной тригонометрической подстановки позволяет преобразовать подынтегральное выражение к дробно рациональному виду.

Метод подстановки позволяет объяснить правило интегрирования .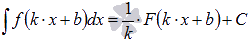

Вводим новую переменную 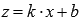, тогда

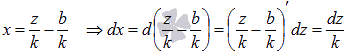
Подставляем полученные выражения в исходный интеграл:

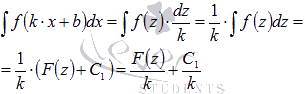
Если принять 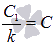и вернуться к исходной переменной х, то получим

Интегрирование по частям.

Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения 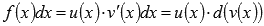и последующем применении формулы 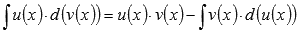. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.

Пример.

Вычислить неопределенный интеграл .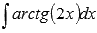

Решение.

Пусть 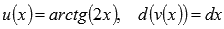, тогда

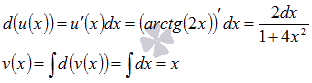
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.

Теперь применяем формулу интегрирования по частям:

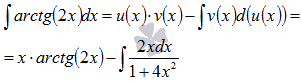
Последний интеграл вычислим по методу подведения под знак дифференциала.

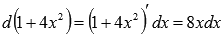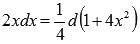Так как , то . Поэтому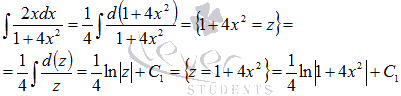

Следовательно,

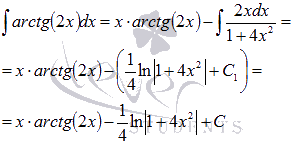
где .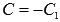

Ответ:

.

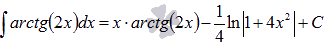Основные трудности при интегрировании по частям порождает выбор: какую часть подынтегрального выражения брать за функцию u(x), а какую за дифференциал d(v(x)). Однако существует ряд стандартных рекомендаций, с которыми рекомендуем ознакомиться в разделе интегрирование по частям.