Определение. Пусть функция 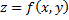 определена в некоторой точке  и в некоторой её окрестности. Если , то функция 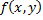 называется непрерывной в точке .

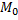Определение. Функция 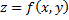 называется непрерывной в точке 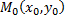, если .

Определение. Множество точек на плоскости называется связным, если любые две точки этого множества можно соединить ломаной, целиком принадлежащей этой области.

Определение. Множество точек на плоскости называется замкнутым, если предельная точка любой сходящейся последовательности точек этого множества также принадлежит этому множеству.

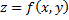Теорема (о непрерывности сложной функции). Если функции  непрерывны в некоторой точке , а функция  непрерывна в некоторой точке , причём , то функция  будет непрерывна в точке .

Теорема (Коши о промежуточных значениях непрерывной функции). Если функция 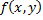 непрерывна в некоторой связной области  и принимает в некоторых двух точках этой области значения  и  ( ), то каково бы ни было число , найдётся такая точка , что .

Доказательство (краткое). Возьмём две точки:  и , причём , ,  (  для определённости). Возьмём точку . Соединим точки  и  ломаной. Если значение функции в некоторой вершине окажется равным , это и будет искомая точка . Если какое-то звено ломаной  непараллельно оси , это звено можно представить через уравнение , следовательно, . Получим функцию, зависящую от одной переменной 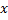, причём  и  удовлетворяют условию, что одна из них меньше , а другая – больше. Тогда по 2-й теореме Коши (см. 1-й семестр) можно утверждать, что . 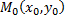Если , то , а значит, точка  является искомой.

Теорема (аналог 1-й теоремы Вейерштрасса). Если функция 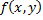 непрерывна в ограниченной замкнутой области , то она ограничена в этой области.

Доказательство (от противного). Допусти, 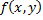 не ограничен сверху, значит, . Пусть 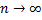. Тогда по теореме Больцано-Вейерштрасса можно выделить подпоследовательность . Эта точка обязательно принадлежит данной области, т.к. по условию  – замкнутая область. Получим:

Данное противоречие показывает неверность допущения и показывает, что 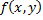 ограничена сверху областью  (снизу – аналогично).

Теорема (аналог 2-ой теоремы Вейерштрасса). Если функция 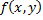 непрерывна в ограниченной замкнутой области , то в области  найдутся, по крайней мере, две точки  и , такие что  – наименьшее значение, а  – наибольшее значение в области .

Определение. Функция 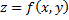 называется равномерно непрерывной, если для сколь угодно малого , такое что для точек  и  из условий  и  следует, что .

Теорема (аналог теоремы Кантора). Если функция 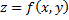 непрерывна в ограниченной замкнутой области , то она равномерно непрерывна в этой области.