АНАЛИЗ И СИНТЕЗ ЛОГИЧЕСКИХ УСТРОЙСТВ АВТОМАТИКИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

АНАЛИЗ И СИНТЕЗ ЛОГИЧЕСКИХ УСТРОЙСТВ АВТОМАТИКИ

При автоматизации различных технологических процессов управляющие устройства во многих случаях должны «принимать решения» в зависимости от выполнения определенных условий.

Пример.Схема автоматической защиты компрессора постоянно осуществляет контроль таких параметров, как давление масла, наличие воды в холодильнике, температура и давление сжатого воздуха в цилиндрах. Если значения этих величин лежат в заданных пределах, то условия нормальной работы компрессора выполняются и его управляющее устройство «принимает решение» о продолжении работы компрессора, в противном случае «принимается решение» об его аварийной остановке.

К управляющим устройствам, “принимающим решение”, относятся системы автоматической защиты, автоматического пуска, остановки и реверсирования машин и механизмов.

Назовем устройства, связанные с принятием решений, логическими. Как правило, схемы таких устройств состоят из элементов, которые имеют на выходе только два состояния: «Включено» — «Выключено», «Высокий» уровень напряжения — «Низкий» уровень напряжения. Аппаратная реализация этих элементов может быть самой различной — электромагнитные реле, логические элементы. В простейшем случае анализ работы и синтез таких схем производят, используя типовые приемы. Однако с усложнением логических схем их построение с использованием имеющегося опыта становится затруднительным или вовсе невозможным. Поэтому при разработке таких схем широко используют алгебру логики.

ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ

Алгебра логики изучает связи между логическими переменными, принимающими только два значения: «Истина» и «Ложь».

Обозначим логические переменные заглавными буквами латинского алфавита A, В, С, … . Припишем каждой из них численное значение 1 или 0 в зависимости от того, является ли переменная истинной или ложной. Тогда численные значения произвольной переменной А равны

Логические 1 и 0 – это не обычные арифметические числа. Они характеризуют состояние переменных, а не их численное значение. Поэтому для алгебры логики действия над переменными отличаются от обычной алгебры.

Рассмотрим основные логические операции.

Логическое сложение.

Сумму любых двух логических переменных записывают в виде А+В и читают А или В. Условимся выражение вида А+В считать ложным в том, и только в том случае, когда обе переменные А и В ложны, т.е. A=0, B=0. В этом случае

Определение логического сложения легко обобщается для любого числа составляющих переменных. В этом случае

Операция логического сложения носит также название дизъюнкции или операции «или».

2. Логическое умножение.

Произведение любых двух переменных записывают в виде АВ и читают А и В.

Условимся выражение вида АВ считать истинным в том, и только в том случае, когда истинны обе переменные А и В, т.е. А=1, В=1.

В этом случае

Определение логического умножения легко обобщается для любого числа составляющих переменных. В этом случае

Операция логического умножения носит также название конъюнкции или операции «и».

Отрицание.

Отрицание переменной A обозначается и читается «не A». Если значение переменной A ложно (A=0), то истинно ( =1), если A истинно (A=1), то ложно ( =0). Это может быть записано в виде следующих правил: . В отличие от логических сложения и умножения операция отрицания производится над одним высказыванием. Операция логического отрицания носит также название инверсии или операции «не».

Для алгебры логики действительны следующие законы.

Закон тождества А=А.

Закон противоречия .

Закон исключения третьего .

Закон двойного отрицания .

Закон идемпотентности АА=А; А+А=А. В силу законов идемпотентности в алгебре логики нет «показателей степеней» и «коэффициентов». Например, ХХХ=Х, а не Х³; Х+Х+Х+Х=Х, а не 4Х.

Переместительный закон (закон коммутативности) для логического сложения и умножения:

1) А+В=В+А,

2) АВ=ВА.

Сочетательный закон (закон ассоциативности) для логического сложения и умножения.

1) А+В+С=(А+В)+С=А+(В+С);

2) АВС=(АВ)С=А(ВС).

Переместительный и сочетательный законы для логических сложения и умножения аналогичны одноименным законам сложения и умножения чисел.

Распределительные законы (законы дистрибутивности)

1) А(В+С)=АВ+ВС;

2) А+(В × С)=(А+В)(А+С).

В отличие от сложения и умножения чисел логические сложение и умножение равноправны по отношению к дистрибутивности: не только умножение дистрибутивно относительно сложения, но и сложение дистрибутивно относительно умножения.

3аконы Де Моргана:

1) , т.е. отрицание логического произведения высказываний равносильно логической сумме их отрицаний;

2) , т.е. отрицание логической суммы высказываний равносильно логическому произведению их отрицаний.

Для алгебры логики справедливы также следующие тождества:

A´1=A; A+1=1; A´0=0; A+0=A.

С помощью логических переменных и символов логических операций можно написать любую логическую формулу.

Приняты три способа представления логических формул:

1. Логическое выражение, которое указывает в явном виде последовательность логических операций, производимых над отдельными переменными А, В, С, … . Например . Порядок вычисления логического выражения следующий: сначала выполняется операция логического отрицания, затем умножения и, наконец, сложения.

2. Таблица истинности, которая позволяет найти значение формулы F в зависимости от различных значений истинности ее переменных. В левой части таблицы перечисляются все возможные комбинации значений истинности логических переменных А, В, С, …, а в правой части — значение истинности логической формулы F. Если имеется n переменных, то число строк таблицы равно 2ⁿ. Составим такую таблицу для формулы . Эта формула содержит три переменные A, В и С. Выпишем в первых трех столбцах таблицы всевозможные сочетания значений истинности для этих переменных. Всего таких сочетаний – восемь. В последующие столбцы запишем значения формул , , , и согласно определениям операций. В результате получим таблицу истинности (табл. 5.1). Первые три и последний столбцы этой таблицы выражают соответствие между всевозможными наборами значений переменных и значениями формулы. Эти столбцы составляют таблицу истинности для формулы . Остальные столбцы являются вспомогательными. Они используются для занесения в них промежуточных результатов вычислений.

Таблица 3.1

Таблица истинности для формулы

A	B	C	A+B
1 1 1 1 0 0 0 0	1 1 0 0 1 1 0 0	1 0 1 0 1 0 1 0	1 1 1 1 1 1 0 0	0 0 0 0 0 0 1 1	0 1 0 1 0 1 0 1	0 1 0 0 0 1 0 0	0 1 0 0 0 1 1 1

3. Логическая схема, которая представляет собой условное графическое обозначение логических операций. Для реализации логических схем используются логические элементы, которые выполняют логические операции сложения, умножения, отрицания. Соединяя соответствующим образом эти элементы между собой, мы можем получить логическую схему, которая реализует определенную логическую формулу. При таком подходе логическая схема, построенная по логическим формулам, позволяет автоматически решать логические задачи, что может быть использовано для целей управления различными процессами.

Рис.3.1. Этапы построения схемы для логического выражения в ДНФ

Применим к данной формуле законы Де Моргана:

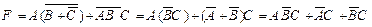Мы получили запись исходного выражения в ДНФ. Построим логическую схему, которая реализует эту функцию. На рис. 3.1, а показан первый этап построения этой схемы. Для получения нужного результата на выходе схемы F отдельные слагаемые 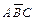, 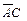и должны быть связаны между собой логическим элементом ИЛИ. На рис. 5.1, б показан второй этап построения логической схемы. 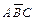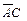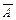Для получения выражений , и в схему добавлены логические элементы И, а для получения на входе элементов И инверсных значений и 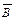используются инверторы. Выходные сигналы с элементов И поступают на вход элемента ИЛИ. Схема, приведенная на рис. 5.1, б, представляет собой логическую схему, которая реализует исходное логическое выражение 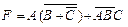, записанное в ДНФ.

Пример. Построить логическую схему для логического выражения 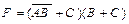, предварительно преобразовав его в конъюнктивную нормальную формулу.

Применим к данной формуле законы Де Моргана

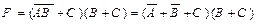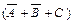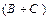Мы получили запись исходного выражения в КНФ. Построим логическую схему, которая реализует эту функцию. Первый этап построения схемы показан на рис. 3.2, а. Для получения нужного результата F на выходе схемы множители этого выражения и должны быть связаны функцией И. На рис. 3.2, б показан второй этап построения логической схемы. Для получения выражени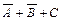й и 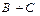в схему добавлены логические элементы ИЛИ, а для получения на входе элементов ИЛИ инверсных значени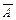й и 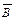используются инверторы. Выходные сигналы с элементов ИЛИ поступают на вход элемента И.

Приведенная на рис. 3.2, б схема реализует исходное логическое выражение 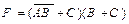, записанное в КНФ.

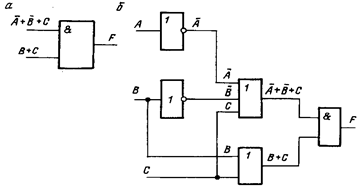Рис.3.2. Этапы построения схемы для логического выражения в КНФ

Необходимо отметить, что при составлении комбинационных логических схем мы использовали только логические элементы И, ИЛИ, НЕ.

Анализируя процесс построения логических схем на основе логических элементов, можно сделать следующие выводы:

1. Перед построением схемы исходное логическое выражение преобразуется в ДНФ или КНФ.

2. Построение логической схемы начинается с ее выхода F. Далее, преобразуя логическое выражение в логические схемы, мы постепенно движемся от выхода к входам схемы (справа налево). В этом и заключается суть построения комбинационных логических схем на основе логических выражений.

3. Логические схемы можно построить на основе логических выражений в ДНФ или КНФ. В первом случае получаются логические схемы типа И – ИЛИ (см. рис. 5.1), а во втором – схемы типа ИЛИ – И (см. рис. 5.2).

СОСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФОРМУЛ ПО ЗАДАННЫМ ТАБЛИЦАМ

ИСТИННОСТИ

Логические формулы – это удобный метод описания принципа работы логической схемы. Однако при проектировании логических схем редко удается выразить решаемые такой схемой задачи непосредственно в виде логической формулы. Обычно на первом этапе синтеза используется словесное описание решаемых схемой задач, на основании которого удается составить таблицу истинности, связывающую численные значения входных и выходных логических переменных. Поэтому необходимо уметь преобразовывать информацию в форме таблицы истинности в логические формулы. Покажем, как это можно сделать.

Пусть дана таблица истинности некоторой, неизвестной пока формулы F, содержащей переменные А, В и С (табл. 3.2).

Таблица 3.2

Таблица истинности для получения логической формулы

Номер строки	A	B	C	F
1 2 3 4 5 6 7 8	1 0 1 0 1 0 1 0	1 1 0 0 1 1 0 0	1 1 1 1 0 0 0 0	1 0 0 1 0 0 0 1

Выделим строки, соответствующие значениям 1 искомой формулы, – это строки 1, 4 и 8. Запишем для каждой из выделенных строк формулу для логического произведения переменных А, В и С или их отрицаний. Причем переменные, имеющие в выделенной строке значение 0, берутся со знаком отрицания, а переменные, имеющие значение 1, – без отрицания. В результате получим следующие формулы логического умножения: 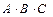для 1-й строки, 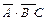для 4-й строки, 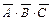для 8-й строки.

Искомой формулой F будет являться логическая сумма полученных произведений

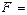
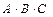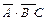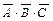+ + . (3.1)

Подобным образом можно составить формулу для всякой таблицы истинности, в последнем столбце которой имеется хотя бы одно значение 1.

Формулу, соответствующую данной таблице, можно получить и другим способом.

Выделим те строки таблицы, в которых искомая формула принимает значение 0, – это строки 2, 3, 5, 6, 7.

Для каждой из выделенных строк составим логическую сумму переменных А, В и С или их отрицаний. Причем переменные, имеющие в выделенной строке значение 1, берутся со знаком отрицания, а переменные, имеющие значение 0, – без отрицания. В результате получим следующие формулы логического сложения: 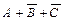(2-я строка), 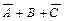(3-я строка), 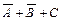(5-я строка), 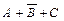(6-я строка), 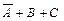(7-я строка).

Искомой формулой F будет являться логическое произведение полученных сумм:

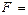
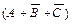
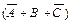
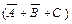
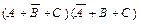. (3.2)

Как видим, первый и второй способы дают для одной и той же таблицы разные логические формулы. Однако, воспользовавшись тождествами математической логики, вторую формулу нетрудно привести к первой.

Рассмотренный метод является универсальным в том смысле, что позволяет получить логическую формулу и в соответствии с ней построить комбинационную схему для любой таблицы. Однако этот метод приводит, как правило, к сложным формулам, для реализации которых требуется большое число различных логических элементов. Поэтому важной задачей синтеза комбинационных схем является задача упрощения или минимизации логических формул.

Рис. 3.4. Карты Карно

Составим карту Карно для логического выражения 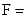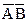+ + 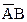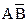. Карта Карно для этого случая показана на рис. 3 4, б. Разместим логические единицы во всех квадратах, которым соответствуют произведения в исходном логическом выражении. Объединим соседние единицы в один контур группами по две, четыре или восемь единиц. Контуры строим до тех пор, пока все единицы не окажутся внутри контуров. Каждому контуру соответствует одно слагаемое упрощенного логического выражения, записанного в дизъюнктивной нормальной форме. На рис. 3.4, б у нас получилось два контура. Следовательно, упрощенное выражение будет состоять из двух слагаемых. Получим это выражение. Возьмем верхний контур. 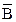Здесь переменная встречается в комбинации с и 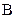. В соответствии с правилами булевой алгебры 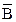+ 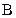=1. Поэтому 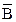и 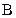здесь опускаются. Тогда в верхнем контуре остается переменная . 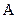Вертикально расположенный контур содержит и Так как + 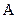=1, то и 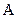также опускаются, остается только 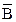. Оставшиеся в результате и 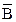затем объединяются посредством операции логического сложения, что приводит к упрощенному логическому выражению = + .

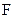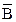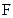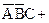
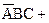
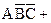
Карты Карно с тремя переменными. Пусть дано логическое выражение = 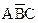. Упростим его с помощью карты Карно. Для случая трех переменных карта Карно содержит восемь квадратов (рис. 3.4, в). Каждый квадрат соответствует одной из возможных комбинаций переменных 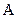, 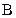и 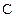. Занесем в квадраты, которые отображают каждое из слагаемых исходного логического выражения, четыре единицы. Возьмем нижний контур. Здесь произведение 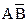встречается в комбинации с 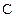и . 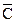Так как 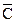+ 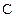=1, то 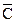и 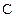можно опустить. Поэтому остается произведение 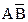. В верхнем контуре переменная 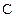встречается в комбинаци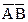и и 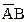. Так как 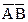+ 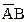= , то в результате остается произведение 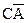. Полученные произведения объединяются посредством операции логического сложения, и мы получаем упрощенное логическое выражение в ДНФ.

= + .

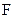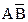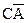Карты Карно с четырьмя переменными. Составим карту Карно для логического выражения

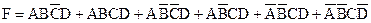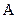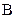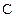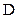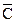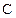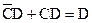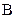Карта Карно с четырьмя переменными (рис. 6.4, г) допускает 16 возможных комбинаций , , и . Этим комбинациям соответствуют 16 квадратов. Нанесем на карту шесть единиц, которые соответствуют шести слагаемым в данном выражении. Группы из двух и четырех единиц объединены квадратами. В нижнем контуре из четырех единиц опускаются и , так как , и и 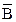, так как 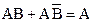. Поэтому нижний контур содержит слагаемое 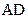. В верхнем контуре переменная 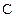встречается в комбинаци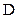и и 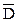, которые можно опустить. После этого верхний контур будет содержать слагаемое 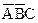. Полученные произведения объединяются посредством операции логического сложения, и Mid получаем упрощенное логическое выражение в ДНФ:

= + .

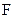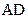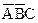Для упрощения логических выражений в рассмотренных случаях применялась одинаковая процедура, которая состоит из следующих операций.

1. Записываем исходное логическое выражение в ДНФ.

2. Заполняем карту Карно. Каждый квадрат при наличии в полученном выражении соответствующих комбинаций входных переменных обозначаем цифрой 1.

3. Соседние единицы соединяем в один контур группами по две, четыре или восемь единиц. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Контуры могут накладываться друг на друга. Для успешного упрощения логического выражения на карте Карно нужно расположить минимальное число контуров, каждый из которых содержит наибольшее число квадратов.

4. Каждый контур представляется в виде логического произведения. Если соседние квадраты в контуре соответствуют прямому и инверсному значениям какой-либо переменной, то эта переменная в данном произведении опускается.

5. Получившиеся для каждого контура логические произведения записываем в виде логической суммы. Это будет результат упрощения исходного логического выражения.

После минимизации логической формулы необходимо составить логическую схему. Для этого необходимо использовать логические элементы ИЛИ, И, НЕ, ИЛИ — НЕ, И — НЕ и другие, выпускаемые промышленностью.

Пример. Требуется создать логическое устройство для управления вентилятором. Вентилятор может быть включен непосредственно (A = 1) или по команде с диспетчерского пункта (B = 1). Вентилятор работает только тогда, когда ток его электродвигателя меньше допустимого значения (логическая функция С = 0). Разобьем решение задачи на несколько этапов.

Этап 1. Составление таблицы истинности (табл. 3.3). В соответствии с условиями задачи заполняем таблицу истинности, в которой записываем значения логической формулы вентилятора F в зависимости от входных логических переменных А, В, С для всех возможных вариантов их сочетаний. При трех входных переменных число таких сочетаний равно 8.

Таблица 3.3

Таблица истинности логического устройства

A	B	C	F	A	B	C	F
1 1 1 1	1 1 0 0	1 0 1 0	0 1 0 1	0 0 0 0	1 1 0 0	1 0 1 0	0 1 0 0

Этап 2. Получение логической формулы. Выделим в таблице истинности строки 2, 4 и 6. Запишем для каждой из выделенных строк формулу для логического умножения переменных A, В и С или их отрицаний. Причем переменные, имеющие в выделенной строке значение 0, берутся со знаком отрицания, а переменные, имеющие значение 1, — без отрицания. В результате получим следующие формулы логического умножения 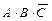для 2-й строки, 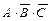для 4-й строки, 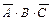для 6-й строки. Искомой формулой 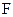будет являться логическая сумма полученных произведений:

+ + .

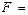
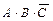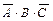Этап 3. Минимизация формулы. Можно создать логическое устройство, которое непосредственно реализует эту формулу. Тогда для выполнения инверсий 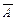, , 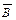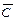потребуется три элемента НЕ, для выполнения логического умножения необходимо три трехвходовых элемента И и для выполнения логического сложения необходим трехвходовый элемент ИЛИ. Всего необходимо использовать семь элементов.

Однако полученную формулу можно упростить. Для этого воспользуемся тождеством 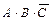= 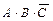+ 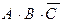и вынесем за скобки общие члены:

+ + + = .

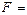
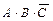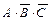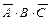Так как 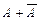=1 и 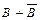=1, то .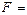

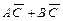
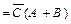Таким образом, воспользовавшись тождествами алгебры логики, мы упростили исходную логическую формулу.

Минимизацию формулы 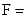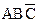+ + 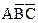можно провести также с помощью карты Карно для трех переменных (рис. 3.5, а). Разместим логические единицы во всех квадратах, которым соответствуют произведения в исходном логическом выражении. Объединим соседние единицы в два вертикальных контура.

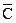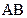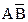Возьмем нижний вертикальный контур. Здесь переменная встречается в комбинации с и . Следовательно, в результате останется произведение 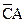. В верхнем контуре переменная 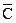встречается в комбинации с 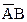и . Следовательно, в результате останется произведение 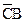. Полученные произведения объединяются посредством операции логического сложения, и мы получаем упрощенное логическое выражение в ДНФ

+ ,

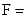
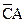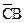
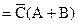что совпадает с полученной ранее формулой.

Этап 4. Построение логической схемы. Минимизированная формула содержит три операции: логическое сложение, логическое умножение, логическое отрицание. В соответствии с этим схема логического устройства, приведённая на рис. 3.5, б, выполнена на логических элементах ИЛИ, И, НЕ.

Выходной логический сигнал F поступает далее на вход системы управления электродвигателя вентилятора и включает его при F=1 или отключает при F=0.

На данном примере мы убедились, какие возможности дает алгебра логики для синтеза логических схем. Порядок решения задачи, разбиваемый на четыре этапа, сохраняется, если разрабатываются и более сложные комбинационные схемы.

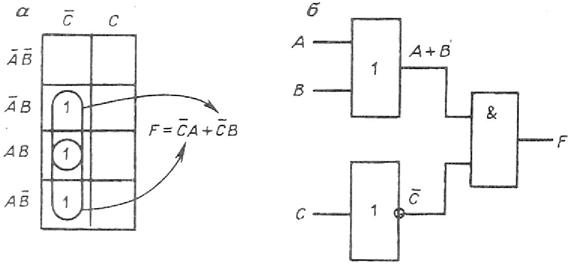
Рис. 3.5. Схема реализации логического устройства управления

Рис. 3.6. Диаграмма тактов логического элемента И.

Рассмотрим на примере методику синтеза последовательной схемы для случая, когда значения выходного сигнала последовательной функции зависят как от комбинации значений входных сигналов в данный момент времени, так от значения выходного сигнала в предшествующий момент времени. Эта зависимость реализуется в виде сигнала обратной связи, подаваемого с выхода схемы на ее вход.

Пример: Управление вытяжными вентиляторами.

В логической системе управления температурой воздуха в помещении установлены два датчика температуры с разными уставками срабатывания Т1 и Т2, причем Т1 ≠ Т2. Эти датчики имеют одинаковую конструкцию и дискретный выходной сигнал. Если температура в месте расположения датчика меньше его уставки, то выходной сигнал равен 0. Если температура равна или больше уставки датчика, то выходной сигнал равен 1. Эти сигналы поступают на вход логической схемы управления вытяжными вентиляторами.

Словесный алгоритм управления работой вентиляторов:

в исходном состоянии сигналы датчиков Т1 и Т2 отсутствуют и вентиляторы отключены; вентиляторы включаются только тогда, когда есть сигналы от обоих датчиков Т1 и Т2; вентиляторы работают до тех пор, пока не исчезнут сигналы от обоих датчиков Т1 и Т2; все входные и выходные сигналы являются дискретными и изменяются в произвольные моменты времени, одновременного изменения значений сигналов Т1 и Т2 быть не может; аварийные и нештатные ситуации не рассматриваются, сигналы блокировок и защиты не учитываются.

Вводим условные обозначения:

Т1 и Т2 – два входных сигнала от датчиков температуры;

Д – выходной сигнал, который управляет включением и отключением электродвигателей вентиляторов;

0 – отсутствие сигнала;

1 – наличие сигнала.

Составляем логические высказывания:

исходное состояние Т1=0 И Т2=0 – Д=0; если Т1=0 И Т2=1 ИЛИ Т1=1 И Т2=0, то Д=0; если Т1=1 И Т2=1, то Д=1; если Т1=0 И Т2=1 ИЛИ Т1=1 И Т2=0, то Д=1; при Т1=0 И Т2=0 – Д=0.

Построим диаграмму состояний согласно заданным словесному алгоритму и логическим высказываниям – рис. 3.7.

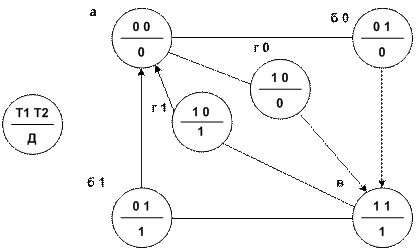
Рис. 3.7. Диаграмма состояний схемы управления вентиляторами.

Диаграмма тактов, приведенная на рис. 3.7, содержит четыре неоднозначных такта: б0, б1 и г0, г1; они свидетельствуют о наличии контуров обратной связи, т.е. это последовательная логическая функция.

Таблица истинности, составленная согласно логическим высказываниям и диаграмме состояний, представлена в таблице 3.4; в ней на наборах 1 и 2 наличие неоднозначных состояний отражено символами 0,1.

Таблица 3.4 – Таблица истинности управления вытяжным вентилятором.

№	Т1	Т2	Д
0	0	0	0
1	0	1	0,1
2	1	0	0,1
3	1	1	1

Минимизация последовательных логических функций проводится аналогично и теми же методами, как и для комбинационных логических функций. Однако, при этом следует выполнить минимизацию двух вспомогательных функций Y 1 и Y 2, где Y 1 – ДНФ при выходном сигнале, равном 1 на неоднозначных тактах; Y 2 – ДНФ при выходном сигнале, равном 0 на неоднозначных тактах. В этом случае ДНФ для заданной последовательной логической функции Y имеет вид:

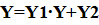Для рассматриваемого примера получим:

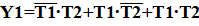
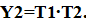
Минимизацию Y 1 и Y 2 выполним методом непосредственного упрощения, в данном примере ее требуется провести только для Y 1, т.е.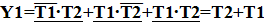

ДНФ для заданной в таблице 3.4 логической функции имеет вид:

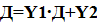Алгоритм управления вентиляторами примет вид:

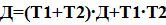ПРИЛОЖЕНИЕ.

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

При разработке дискретных систем управления применяют формализованные методы синтеза и методы формального описания их условий работы. Целью этого подхода является исключение влияния субъективных факторов, связанных с разработчиком, и получение однозначного наилучшего конечного решения при проектировании.

Выбор и составление функциональной и структурной схем дискретной системы управления осуществляется на основании технического задания на проектирование. Техническое задание составляется совместно заказчиком и разработчиком. После его согласования и утверждения оно является основным документом для проектирования системы управления.

Основными разделами технического задания являются:

1 - основание для разработки системы, ее назначение и область применения;

2 - условия эксплуатации электрооборудования;

3 - эксплуатационно-технические характеристики системы;

4 - объем выполняемых разработчиком работ;

5 - технические требования к системе;

6- требования к конструкторскому оформлению системы;

7 - требования к патентной защищенности проекта;

8- требования к заказчику по обеспечению разработки, внедрению и эксплуатации системы.

1 раздел должен содержать:

- стоимость работ, сроки начала и конца разработки, вид окончания разработки (проект, опытный образец, серия и т.д.);

- режимы работы объекта, описание каждого режима, правила перехода с режима на режим, правила стыковки системы управления с объектом и т.д.;

- технико-экономическое обоснование необходимости разработки системы, данные о сроках ее окупаемости.

Совокупность этих сведений представляет собой алгоритм функционирования дискретной системы управления. В этом разделе перечисляют аварийные и внештатные ситуации, описывают порядок работы в пуско-наладочном и ручном режимах управления.

2 раздел должен содержать:

- климатические условия эксплуатации электрооборудования;

- механические условия работы (вибрация, тряска т др.);

- наличие и виды электромагнитных помех;

- условия электропитания схемы управления;

- характер работы системы (непрерывный, циклический и др.);

-условия ремонта и обслуживания средств управления;

- технико-экономические и другие последствия возможных отказов системы управления;

- меры по технике безопасности при обслуживании системы управления..

3 раздел должен содержать:

- сведения о дополнительных функциях, реализуемых системой управления (сигнализация о неисправностях, регистрация необходимых параметров, самоконтроль и диагностика системы и др.);

- комплектность основного и резервного оборудования.

4 раздел должен содержать:

- этапы работ и объем разработки по каждому этапу, сроки выполнения этапов и возможные исполнители;

- изготовители образцов по каждому этапу работ.

5 раздел должен содержать:

- данные об интенсивности и составе информационных потоков, входящих в систему управления, количество обслуживаемых процессов с их перечислением;

- режимы работы системы управления (автоматический, ручной, наладочный и др.);

- потребляемую мощность, характер источника питания и его параметры;

- техническую характеристику системы управления и входящих в нее составных частей (быстродействие или максимальное запаздывание, надежность, ремонтопригодность, тип элементной базы и др.);

- требования к взаимозаменяемости блоков и необходимость применения унифицированных и стандартизованных изделий.

6, 7, 8 разделы не относятся к рассматриваемой в настоящем пособии теме, поэтому они в этом материале не рассматриваются.

К техническому заданию прилагаются расчет технико-экономической эффективности, сетевой график выполнения работ, данные об объекте, необходимые разработчику.

Техническое задание содержит сведения по управлению конкретным технологическим объектом, получаемые разработчиком и согласованные с заказчиком. Это перечень основных технологических режимов работы всего оборудования и условий переходов с одного режима на другой. Информация о режимах работы объекта предполагает знание параметров всех его исполнительных механизмов, количество и типы всех воспринимающих устройств.

На основе характеристик исполнительных механизмов определяют количество выходных сигналов системы управления, а по параметрам воспринимающих элементов определяют количество входных сигналов. В итоге разработчиком составляется и описывается словесно структурная схема системы дискретного управления для конкретного технологического процесса – эта схема должна быть аналогичной рисунку 2.1.