Определим оптимальную оценку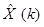 
вектора состояния 
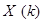в расширенном пространстве состояния как условное математическое ожидание
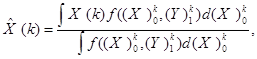
Рассмотрим одношаговую задачу в рамках байесовского подхода
полагая, что известна совместная плотность распределения величин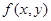 
В такой постановке оптимальная задача оценивания вектора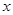 
может быть решена как
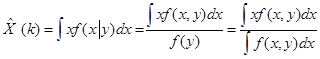
при этом действительная ковариационная матрица ошибки оценки определяется выражением
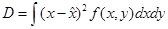
Оптимальные оценки в классе линейных оценок
Упрощение решения задачи оценивания можно достичь, ограничив класс получаемых оценок
Рассмотрим поиск оптимальных оценок в классе линейных оценок вида
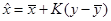
Где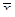 
и 
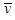- математические ожидания параметров
Нетрудно видеть, что
.
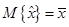Такая байесовская оценка называется несмещенной
Определим ковариационную матрицу ошибки оценки
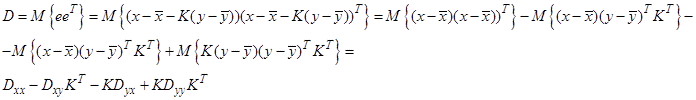
Выделим теперь из этого выражения полный квадрат
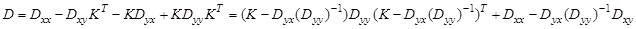
С учетом того, что первое слагаемое, по крайней мере, положительно полуопределенная матрица, очевидно, что минимальное значение будет достигаться при
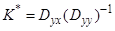
При этом минимальное значение ковариационной матрицы будет равно
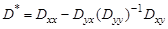
Из выражения для оценки и ковариационной матрицы вытекает,что они могут быть вычислены, если известны параметры ,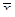 
, 
, 
.
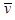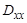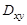
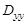Решение линейной задачи
Будем полагать, что известна совместная плотность распределения с матрицей вторых центральных моментов
,
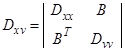а измерения линейны
.
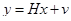В этом случае можем записать для вектора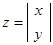 
выражение для ковариационной матрицы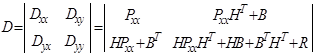 
Если ошибки не коррелированны, т.е.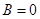 
имеем
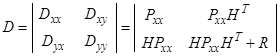и, как следствие формулы оптимального линейного фильтра принимают вид
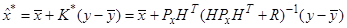
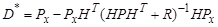
Линейный оптимальный алгоритм в линейной задаче не зависит от вида распределения оцениваемого вектора и ошибок измерения.
Решение нелинейной задачи
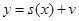
Рассмотрим решение нелинейной задачи, полагая, что известна совместная плотность распределения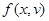 
Для использования линейного оптимального алгоритма необходимо знание следующих параметров:, ,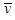 
, 
.
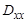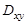
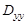Эти параметры могут быть определены следующим образом
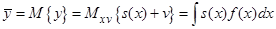
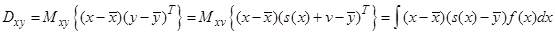
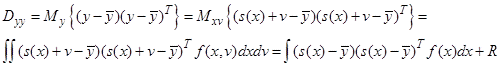
Отметим, что кроме знания моментов требуется также знание плотности распределения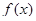 
Пример
, 
, 
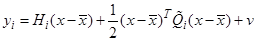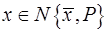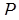-диагональная матрица
Введем обозначения
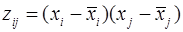. Вектор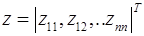 
Тогда
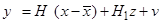
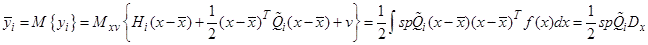
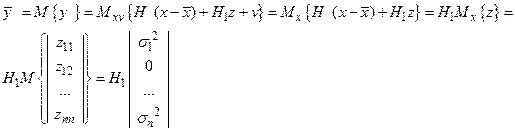
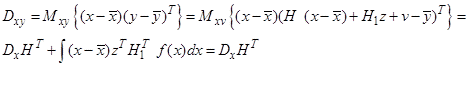
Здесь учтено, что нечетные центральные моменты гауссовской плотности равны нулю.
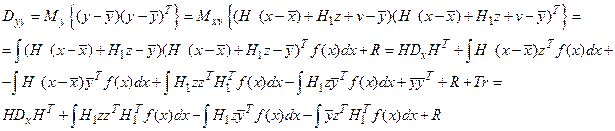
Рассмотрим 
.
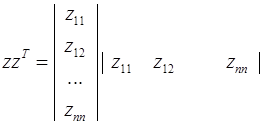Нетрудно заметить, что для случая некоррелированности компонент вектора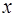 
это произведение будет диагональной матрицей с элементами
.
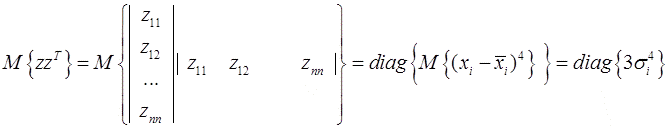Рассмотрим члены
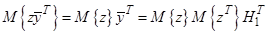
и произведение
.
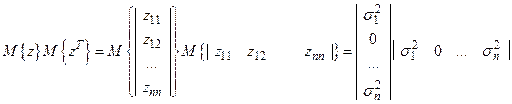Нетрудно заметить что это произведение будет матрицей содержащей ненулевые элементы вида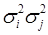 
Байесовский подход. Оптимальные оценки
Выше было показано, что для нахождения оптимальной оценки в рамках байесовского подхода требуется вычисление интеграла
,
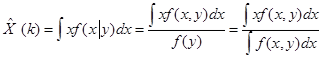при этом средняя действительная ковариационная матрица ошибки оценки определяется выражением
, 
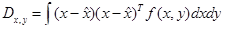
а условная ковариационная матрица выражением
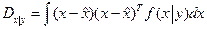
Свойства оптимальных оценок
Свойство 1. Несмещенность оценки
Действительно имеем
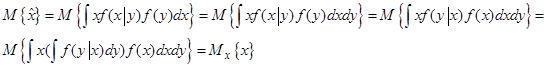
Свойство 2. Ортогональность ошибки оценки
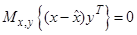
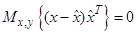
Дата: 2018-12-28, просмотров: 248.
