Определение 3.26. Точка 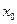, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается одно из условий непрерывности функции.

Если существуют конечные пределы:

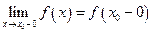 и ,

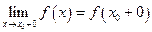причем не все три числа 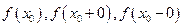 равны между собой, то  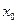называется точкой разрыва I рода.

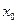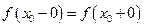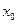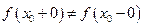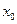В частности, если левый и правый пределы функции в точке  равны между собой: , но не равны , то  называется устранимой точкой разрыва, если , то  называется точкой скачка функции.

Точки разрыва, не являющиеся точкам» разрыва I рода, называются точками разрыва II рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов.

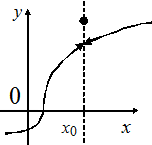
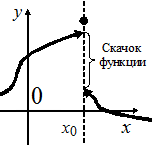
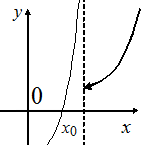
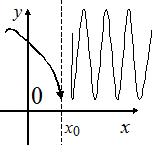
Рис. 3. 24              Рис. 3. 25                       Рис. 3. 26                  Рис. 3. 27

Пример 3.25. Показать, что при  функция 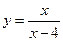 имеет разрыв.

Решение. Это элементарная функция с областью определения D(y)=(-∞,4) 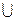(4,+∞) имеет разрыв только в точке 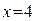. Находим ,

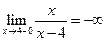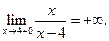
Таким образом, функция при x®4 не имеет ни левого, ни правого конечного предела. Следовательно, 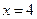 яв­ляется точкой разрыва II рода (Рис. 3.28).

Пример 3.26. Показать, что при 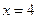функция  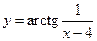имеет разрыв.

Решение. D(y)=(-∞,4) 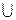(4,+∞) Если x®4 – 0, то 1/(x-4)® -¥ и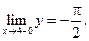

Если x®4 +0, то 1/(x-4)®+¥ и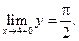

Итак, при x®4 функция имеет левый и правый конечные пределы, причем эти пределы различны. Следовательно, х=4 является точкой разрыва I рода (Рис. 3.29).

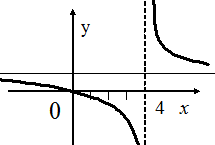
       Рис. 3.28                                                               Рис. 3.29

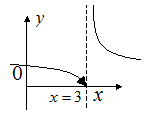Разность между правым и левым пределом в точке разрыва I рода называется скачком. В данном примере скачок равен  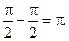(Рис. 3.29).

Пример 3.27. Исследовать на непрерывность функцию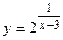  

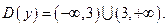
Решение. Это элементарная функция. Поэтому она имеет разрывы только в точках, в которых она не определена. Следовательно, имеется одна точка разрыва 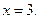 Исследуем характер разрыва.

Рис. 3.30

,

.

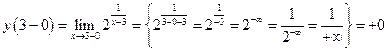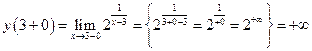В точке функция имеем разрыв второго рода. Тип разрыва можно установить, построив график функции

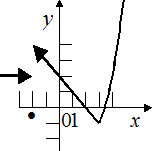Пример 3.28. Исследовать на непрерывность неэлементарную функцию

Решение. 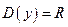. Из графика видно, что функция имеет разрыв первого рода в точке  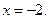Кроме того, ,

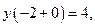
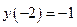В точке 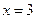выполнено: , ,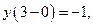

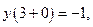
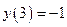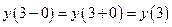т. е. функция непрерывна.                                        Рис. 3.31

Асимптоты

Определение 3.27. Прямая называется асимптотой для кривой, если расстояние от точки кривой до этой прямой стремится к нулю при отдалении точки в бесконечность.

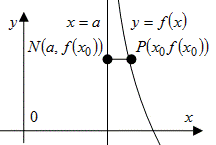
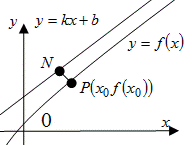
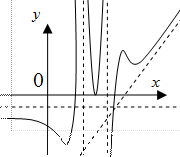
     Рис. 3.32                          Рис. 3.33                                  Рис. 3.34

Из рис. 3.34 можно сделать вывод, что график функции может иметь любое число (в том числе бесконечное множество) вертикальных асимптот, но не более двух наклонных или горизонтальных: левую и правую. График функции может пресекать наклонные и горизонтальные асимптоты, но не может пересекать вертикальные асимптоты. Выведем уравнения асимптот.

Рассмотрим вначале вертикальные асимптоты.

Пусть график функции имеет вертикальную асимптоту 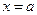. Возьмем точку  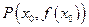на графике функции. В этом случае обязательно 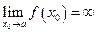, так как в противном случае точка Р не удалялась бы неограниченно от начала координат. Верно и обратное утверждение: если 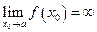, то 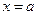 — вертикальная асимптота. Таким образом,  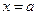— вертикальная асимптота, если .

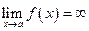Чтобы установить взаимное расположение ветвей линии и асимптоты исследуют знак бесконечности 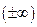, к которому стремится 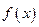, когда х стремится слева и справа к точке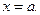

Поэтому вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения в конечных точках (открытые концы области определения).

Пусть 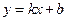 — наклонная асимптота. Возьмем точку  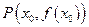на графике функции. Из определения асимптоты .

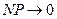 Используя формулу расстояния от точки до прямой имеем 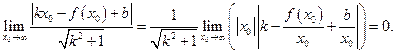 Отсюда тем более и  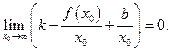Предел третьего слагаемого равен нулю, поэтому, получаем  Но так как 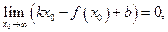 то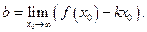

Таким образом, если существует наклонная асимптота , то ее параметры находятся по формулам ,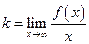

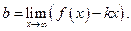
Ясно, что верно и обратное: если эти пределы существуют, график функции имеет асимптоту. Если бы, хотя бы один из пределов не существует, то наклонной асимптоты нет.

Для горизонтальной асимптоты 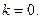 Поэтому горизонтальная асимптота имеет уравнени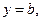е  где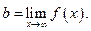

Если асимптотическое изменение функции различно при стремлении х к положительной или к отрицательной бесконечности, то следует раздельно рассматривать случаи 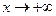 и

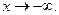
Пример 3.29. Найти вертикальные и горизонтальные асимптоты графика функции .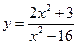

Решение. D(y)=(-∞,-4) 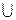(-4,4)  (4,+∞). Следовательно, исследуем точки±4.

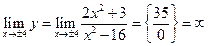. Поэтому линия имеет две вертикальные асимптоты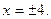

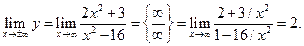 Поэтому линия имеет одну горизонтальную асимптоту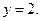

Пример 3.30. Найти асимптоты графика функции .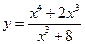

Решение. D(y)=(-∞,2) 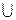 (2,+∞). Линия имеет оду вертикальную асимптоту, горизонтальных асимптот не имеет. Наклонные ищем в ви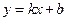де , где

,

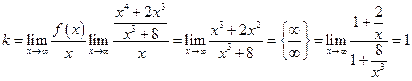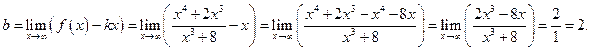Линия имеет наклонную асимптоту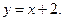

Ее можно найти выделением линейной части:

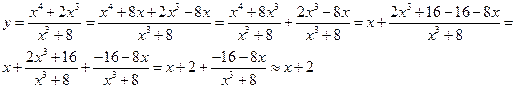
при больших х.

3.3.4. Основные свойства функции, непрерывной на отрезке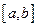

Перечислим, не доказывая, основные свойства функции, непрерывной на отрезке .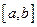

Теорема І. Всякая непрерывная на отрезке 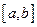 функция ограничена на этом отрезке (Рис. 3.35).

Определение 3.28. Наибольшим (наименьшим) значением функции 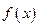 на отрезке  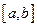называется такое значение 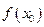, что для всех точек х отрезка  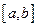выполняется неравенство .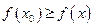

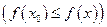Теорема 2. Функция, непрерывная на отрезке 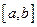, принимает, по крайней мере, в одной его точке наибольшее значение и по крайней мере в одной его точке — наименьшее значение (Рис. 3.36).

Теорема 3. Функция, непрерывная на отрезке 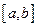, принимающая на концах этого отрезка значения противоположных знаков, по крайней мере, в одной точке отрезка  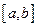обращается в нуль (Рис. 3.37).

Теорема 4. Функция, непрерывная на отрезке 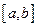, принимает в этом отрезке все промежуточные значения между своими наибольшим и наименьшим значениями, соответственно М и m.

Примечание. Из определения функции, ограниченной на отрезке 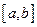, следует, что график такой функции целиком располагается между прямым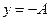и  и . Например, график функции 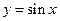, как известно, целиком располагается между прямым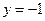и  и .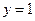

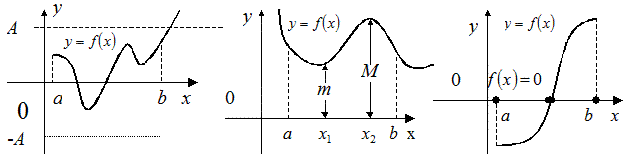                       Рис. 3. 35                          Рис. 3. 36                            Рис. 3. 37

ЛИТЕРАТУРА

Для содержательных модулей

1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.

2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.

Основная

1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.

2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.

3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.

4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.

5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.

6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.

7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.

8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.

Сборники задач

1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.

2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.