Теорема (о производной сложной функции)

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

_____________________________________________________________

ФИЛИАЛ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)»

В г. Смоленске

В.Н. Денисов, В.И. Бобков,

Е.И. Выборнова, Н.Ф. Кулага

МАТЕМАТИКА

УЧЕБНЫЙ ПРАКТИКУМ

и контрольные задания

для студентов заочной формы обучения

Семестр

Смоленск 2010

УДК 51 (076)

М-34

Утверждено учебно-методическим Советом филиала ГОУВПО «МЭИ (ТУ)» в

г. Смоленске в качестве учебно-методического пособия для
студентов 1 курса заочной формы обучения

Рецензент:

Кандидат технических наук, доцент филиала ГОУВПО «МЭИ (ТУ)» в г. Смоленске
А.В. Борисов

П69

Математика. Учебный практикум и контрольные задания для студентов заочной формы обучения 1 семестр.[Текст]: учебно-метод. пособие / Сост.: В.Н. Денисов, В.И. Бобков, Е.И. Выборнова, Н.Ф. Кулага – Смоленск: РИО филиала ГОУВПО «МЭИ (ТУ)», 2010 г. – 52 с.

Пособие предназначено для студентов заочной формы обучения 1 курса технических специальностей при изучении курса высшей математики в первом семестре. Представлен материал разделов «Линейная алгебра», «Аналитическая геометрия», «Пределы», «Дифференцирование», «Функции нескольких переменных». Содержание излагаемого материала полностью соответствует тематическому плану курса.

ВВЕДЕНИЕ

Материал данного пособия предназначен студентам первого курса заочной формы обучения СФ «МЭИ(ТУ)». В данном пособии приведены рекомендации по изучению теоретического материала, примеры решения задач, задачи расчетного задания.

В рекомендациях по изучению теоретического материала указана литература и разделы, соответствующие разделам учебной программы.

В других разделах пособия приведены примеры решениях типовых задач, задачи расчетного задания.

При изучении материала студентам вначале нужно проработать его теоретическую часть по лекциям и указанной в рекомендациях литературе. Затем разобрать приведенные в лекциях и рекомендованной литературе примеры на закрепление теоретического материала. После решить задачи расчетного задания и подготовиться к его защите.

РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

Программа курса для первого семестра обучения состоит из следующих разделов:

1. Матрицы, действия над ними. Алгебра матриц.

2. Определители, их свойства. Миноры. Алгебраические дополнения. Разложение определителя по строке и столбцу. Метод Гаусса..

3. Обратная матрица, ee свойства. Ранг матрицы, его свойства. Матричные уравнения.

4. Системы линейных алгебраических уравнений. Правило Крамера. Теорема Кронеккера-Капелли.

5. Однородные системы. Структура общего решения неоднородной системы.

6. Таблица межотраслевого баланса, модель Леонтьева.

7. Собственные числа и собственные векторы квадратных матриц.

8. Векторы, действия над ними, базис, координаты. Линейная зависимость и независимость векторов.

9. Скалярное, векторное и смешанное произведения векторов.

10. Плоскость и прямая и в пространстве. Различные способы задания прямой и плоскости в пространстве. Расстояние от точки до плоскости. Углы между прямыми и плоскостями.

11. Кривые второго порядка на плоскости, классификация кривых. Канонические уравнения эллипса, параболы, гиперболы.

12. Поверхности второго порядка. Канонические уравнения поверхностей второго порядка.

13. Понятие функции, способы задания функции. Понятие и определение предела функции в точке.

14. Свойства функций, имеющих предел. Бесконечно малые и бесконечно большие функции, их свойства и сравнение. Эквивалентные функции.

15. Непрерывность функции в точке. Свойства непрерывных функций. Классификация разрывов. Функции, непрерывные на отрезке. Последовательности.

16. Дифференцируемость функции в точке. Дифференциал и производная функции, их геометрический смысл. Производная суммы, произведения и частного.

17. Производная сложной функции, обратной функции. Производные и дифференциалы высших порядков. Формула Лейбница. Теоремы о среднем для дифференцируемых функций, правило Лопиталя. Формула Тейлора.

18. Возрастание (убывание) функций. Экстремумы функций. Необходимое условие экстремума, достаточное условие экстремума. Выпуклость, точки перегиба, условия их существования. Общая схема исследования функции с построением графика.

19. Функции нескольких переменных.

Изучение материала курса полезно проводить, придерживаясь тем и рекомендуемой литературы.

1. ТЕМА.

Матрицы, определители, системы линейных уравнений.

После изучения раздела студент должен знать: определение матрицы, типы матриц (квадратные, прямоугольные, единичные), операции над матрицами, определители матриц и их свойства, системы линейных уравнений и методы их решения (правило Крамера, метод Гаусса, метод обращения матриц).

Литература:[1,2].

2. ТЕМА.

Векторы, действия над ними, скалярное, векторное, смешанное произведения. Плоскость, прямая, кривые второго порядка, квадратичные формы.

После изучения раздела студент должен знать: понятие вектора, операции над векторами, разные типы произведений векторов, разные виды уравнений прямой, плоскости, канонические уравнения кривых второго порядка.

Литература:[1,2].

3. ТЕМА.

Понятие множества и функции, примеры множеств (натуральные, целые, рациональные и иррациональные числа) и функции (элементарные функции). Понятие предела функции в точке и непрерывности функции в точке.

После изучения раздела студент должен знать: символику для работы с множествами, графики основных элементарных функций, геометрический смысл предела функции, определение предела, его свойства и методы нахождения, непрерывность в точке и точки разрыва.

Литература:[1,2].

4. ТЕМА.

Понятие производной функции в точке, ее геометрический и экономический смысл. Вычисление производных при помощи таблицы. Дифференцируемость и дифференциал. Правило Лопиталя. Высшие производные. Исследование функций. Построение графиков.

После изучения раздела студент должен знать: таблицу производных, физический и геометрический смысл производной, уметь вычислять производные при помощи таблицы и свойств, исследовать функции и строить графики.

Литература:[1,2].

5. ТЕМА.

Функции нескольких переменных, их производные. Основные теоремы. Задачи на экстремум.

Литература:[1,2].

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Расчетное задание состоит из десяти заданий. Для выполнения расчетного задания будут полезны образцы решения задач, приведенные ниже.

Задание 1. Даны матрицы

Найти определитель матрицы

Вычислить результирующую матрицу .

Образец решения задания.

Пусть

Вычислим определитель матрицы разложением по первой строке:

Произведем действия над матрицами с учетом свойств матриц

= .

После транспонирования матрицы имеем выражение

Перемножая матрицы, получим

Складывая соответствующие элементы двух полученных матриц, видим, что

Задание 2. Решить методом Гаусса и как матричное уравнение систему линейных уравнений.

Суть метода Гаусса состоит в том, что при помощи преобразований, не нарушающих равносильности, исходная система сводится к треугольному виду.

Пример.

При решении систем методом исключения Гаусса вначале составим расширенную матрицу системы уравнений.

Преобразуем при помощи метода исключения Гаусса к диагональному виду, составляя линейные комбинации строк, чтобы получить нулевые элементы ниже главной диагонали

Шаг 1

= .

Шаг 2

Переход к равносильной треугольной системе называют прямым ходом метода Гаусса. Выражая из треугольной системы , затем , затем , то есть, выполняя обратный ход метода Гаусса, легко находим решение системы.

Равносильные преобразования в методе Гаусса - это линейные комбинации строк матрицы.

Для иллюстрации метода Гаусса рассмотрим примеры.

Пример:

Решить систему уравнений:

Шаг 1: Делим коэффициенты первого уравнения на коэффициент а₁₁¹0, при этом получается равносильная система уравнений.

Шаг 2: На месте 2 и 3 уравнений поставим сумму 1-го уравнения, умноженного на (-1), и 2,3- уравнений. На месте 4-го уравнения сумму 1-ой строки, умноженную на (-2), и 4-ой строки. Для краткости записей воспользуемся понятием расширенной матрицы и эквивалентных преобразований

Т. к. во 2, 3, 4 уравнениях неизвестное х₁- исключено, то применим схему приведенную выше для исключения неизвестных в системе, состоящей из 2, 3, 4 уравнений. Для этого вторую строку разделим на 1/2, на месте 3, поставим сумму элементов 2 строки, умноженную на (-7/2), и 3-й строки на месте 4-ой строки сумму элементов 2 строки умноженную на (-1) и 4 строки.

Исключая неизвестные в 3 и 4 уравнениях по той же схеме завершим прямой ход метода Гаусса.

Используя обратный ход метода Гаусса, имеем:

Если матрица А невырождена ( ), то для нее существует обратная матрица, обозначаемая А^-1 , такая, что А^-1×А = А×А^-1= Е, где Е – единичная матрица. Используя это свойство, можно решить матричное уравнение так:

А×Х = В Û А^-1×А×Х = А^-1×В Û Е×Х = А^-1×В,

т.е.

Х = А^-1×В

В том случае, когда матричное уравнение имеет вид A X×C = B , то схема решения такова:

А^-1×А× Х× C× C^-1= А^-1× В×C^-1 Û Х = А^-1× В×C^-1

Пример.

Задание 3. Треугольник ABC задан координатами его вершин: A(-2,1,3), B(1,-2,-3), C(2,-3,-1).

Найти

1). Площадь треугольника ABC;

2). Косинусы углов треугольника;

3). Высоту, опущенную из вершины А на сторону ВС;

4). Определить, параллелен ли вектор плоскости треугольника АВС.

Решение.

Найдем координаты векторов АВ=(1+2,-2-1,-3-3)=(3,-3,-6), АС=(4,-4,-4), ВС=(1,-1,2). Так как площадь треугольника равна половине площади соответствующего параллелограмма, то, используя геометрический смысл векторного произведения векторов, найдем площадь треугольника как половину модуля векторного произведения векторов, на которых построен треугольник.

Углы треугольника легко определить, используя скалярное произведение векторов. Например, для угла А имеем:

Для отыскания высоты, опущенной из вершины А на сторону ВС, разделим площадь треугольника на длину стороны ВС, т.е. на модуль вектора ВС.

Узнать о параллельности вектора можно при помощи смешанного произведения векторов . Если оно равно 0, то векторы компланарны, т.е. лежат в одной плоскости, если не равно 0, то некомпланарны. Найдем смешанное произведение векторов:

Значит, вектор не параллелен плоскости треугольника АВС.

Задание 4. Задана прямая и плоскость

Найти

1). Угол между прямой и плоскостью в градусах, округлив результат до единиц градусов;

2). Точку пересечения прямой и плоскости, если она существует.

Решение.

Угол между прямой и плоскостью можно найти как, дополняющий до прямого, угол между направляющим вектором прямой и нормальным вектором плоскости , используя скалярное произведение векторов. Так как

Значит угол равен - .

Для определения точки пересечения прямой и плоскости запишем совместно параметрические уравнения прямой и уравнение плоскости, и решим их путем подстановки первого, второго и третьего выражений в четвертое уравнение. После чего получим:

Задание 5. Найти пределы функций.

При нахождении пределов функции пользуются следующими свойствами пределов и теоремами:

1).Предел константы равен самой константе.

k=k.

2). Если существует ($) f(x)=А (конечный), $ g(x)=B (конечный), то:

- предел суммы (разности) этих функций х®х₀ существует и равен сумме (разности) пределов

(f(x) g(x))= f(x) g(x);

- предел произведения существует и равен произведению пределов

[f(x)×g(x)]= f(x)× g(x);

- предел частного функций существует и равен частному пределов

, В¹0.

3). Пределы основных элементарных функций равны значениям этих функций в точке, где ищется предел.

Например

, , ,

При нахождении пределов нельзя пользоваться рассмотренными выше свойствами, если:

1) f(x)®0, j(x)®0, при x®x₀ и ищется предел вида . В этом случае говорят о наличии неопределенности вида ноль делить на ноль .

2) f(x)®0, j(x)®¥, при x®x₀, то о пределе вида , говорят как об имеющем неопределенность ноль умножить на бесконечность.

3) f(x)® +¥, j(x)® +¥, при x®x₀, то говорят, что имеет неопределенность вида .

4) f(x)® ¥, j(x)® ¥, при x®x₀, то говорят, что имеет неопределенность бесконечность делить на бесконечность.

При нахождении пределов в этих случаях нужно вначале избавиться от неопределенности и лишь после этого применять теоремы и свойства пределов. С этой целью, как правило, выделяют в числителе и знаменателе одинаковые множители, стремящиеся к нулю или к бесконечности, или избавляются от иррациональности умножением на сопряженное выражение или применяют эквивалентные функции.

Пример:

= = =

При нахождении пределов применяют теоремы о связи бесконечно-малых и бесконечно-больших функций и теорему о пределе показательно-степенной функции:

Если y=f(x), при x®x₀ бесконечно малая функция(f(x)->0), то [1/f(x)]-> при x®x₀ - бесконечно большая функция и наоборот, если j(х)- бесконечно большая функция при x®x₀, то [1/j(x)]- бесконечно малая функция при x®x₀.

Пример:

Вычислить:

Порядок роста (наибольший показатель степени у слагаемых) числителя и знаменателя один и тот же и равен 11.

Делим числитель и знаменатель на и учитывая связь бесконечно больших и бесконечно малых функций, имеем:

Если и то существует
предел показательно-степенной функции, причем .

При этом если

1) 0<A<1;

2) A>1;

3) 0<A<1,

4) A>1,

Если же U®1, V®¥, при x®x₀, то говорят о неопределенности вида {1^¥}:

неопределенность.

Для раскрытия неопределенности такого вида применяется формула

Примеры:

Задание 6. Найти производную заданной функции.

При нахождении производных функции в точке и на интервале применяют таблицу производных, их свойства и теоремы о производных.

Таблица производных:

Свойства производных.

Если существуют производные функций и в точках интервала , а и постоянные множители, то:

1. Производная суммы (разности) функций равна сумме (разности) производных, константы можно выносить за знак производной, при этом справедлива формула:

Пример:

2. Производная произведения вычисляется по формуле:

Пример:

3. Производная частного (дроби) вычисляется по формуле:

Пример:

Найти , если
Используя свойство производной суммы и переходя от арифметических корней к степенным функциям, имеем:

Применяя таблицу производных и формулы для дифференцирования произведения и частного, получим

= =

= .

При нахождении производных часто применяется следующая теорема.

Определение:.

Если на интервале 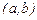существует производная от первой производной функции 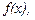то она называется второй производной от 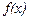на интервале 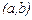и обозначается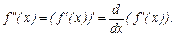

Пример:

Найти вторую производную функции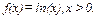

Так как 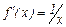, то .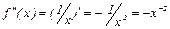

Аналогично можно ввести производные более высокого порядка.

Определение:

Пусть у функции 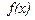существует производная порядка "n-1" на интервале 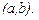Если на этом интервале существует производная от производной порядка " n-1" функции 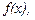то она называется производной порядка "n" и обозначается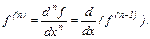

Пример:

Найти пятую производную функции 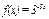. Производя последовательные дифференцирования, имеем

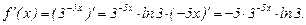
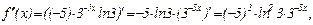
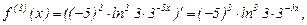
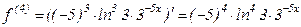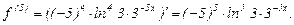
Здесь принято, что производные до второго порядка включительно обозначаются штрихами, производные более высокого порядка обозначаются верхним индексом в скобках. Очевидно, что для нахождения производных высоких порядков нужно последовательно применить первую производную к функции, ее первой производной, второй производной и так до производной нужного порядка.

Заметим, что если существует производная порядка "n", то все производные более низких порядков также существуют. Обратное неверно.

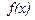Пусть на интервале ( существуют производные порядка "n" у функций и 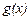тогда справедливы свойства:

1.Линейность.

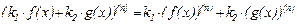где 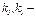константы.

2.Формула Лейбница

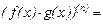
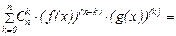
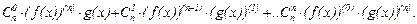
Здесь принято, что знак 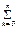- обозначает сумму "n+1" слагаемых, получающихся при изменении индекса от нуля до "n", а числа 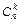вычисляются по формуле:

= .

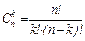Пример:

Вычислить пятую производную 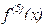, если .

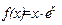Используя формулу Лейбница, имеем:

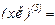
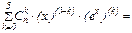
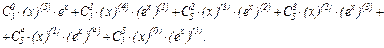
Так как 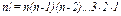, в частности 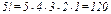, то

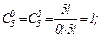
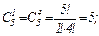
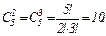
Найдем производные функци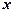й и , производя последовательные дифференцирования:

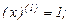
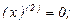
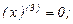
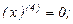
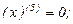
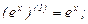
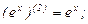
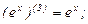
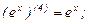
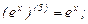
Подставляя найденные производные и числа в формулу Лейбница, получаем:

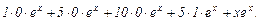
После преобразования имеем:

= .

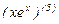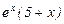Задания 8, 9. Построить график функции.

Полное исследование функции 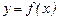и построение ее графика рекомендуется проводить по схеме:

1. Найти область определения функции D ( x )– множество значений аргумента, при которых функция имеет смысл.

2. Исследовать функцию на периодичность, четность и нечетность.

Если 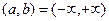и существует такое числ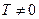о , что для любого 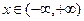, то исследуемая функция периодична с периодом 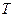. При этом достаточно построить график функции на промежутке 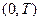и доопределить его по периодичности на всю числовую ось.

Если 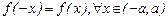, то исследуемая функция четная, в этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке 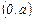и отобразить его симметрично относительно оси ординат на .

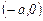Если 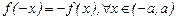, то исследуемая функция нечетная, в этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке 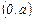и отобразить его симметрично относительно начала координат на .

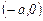3. Асимптоты. Для их нахождения установить характер точек разрыва функции (если они имеются), исследовать поведение функции в точках разрыва и при 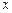стремящемся к бесконечности.

Если в точке 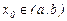функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту 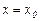(прямая называется асимптотой кривой, если расстояние от точки кривой до этой прямой по мере удаления точки в бесконечность стремится к нулю).

Если при 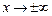существуют и конечны пределы 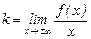и 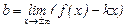, то прямые вида 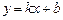называются наклонными асимптотами графика функции .

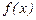4. Найти экстремумы функции (max или min) и интервалымонотонности функции (возрастания, убывания).

Если на (а, b) производная 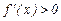, то функция 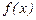возрастает на этом интервале, при 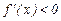функция 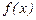на интервале убывает.

Для отыскания точек экстремума применим следующие приемы:

1) Если в окрестности критической точки первой производной х₀ (эти точки ищут из условий: y' не существует или y'=0) первая производная функции непрерывной функции меняет знак, то в точке 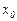есть экстремум, причем при смене знака производной с “-” на “+” в точке 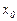имеется минимум( f ( x ₀ )= f_min ) при смене знака с “+” на “-” в точке 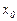имеется максимум( f ( x ₀ )= f_max ).

2) Если в критической точке 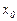производная 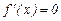, но вторая производная 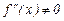, то точка 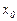- точка экстремума, при этом при значении 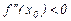в точке 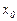имеется максимум ( f ( x ₀ )= f_max ), если же 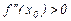, то в точке 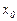имеется минимум( f ( x ₀ )= f_min ).

5. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.

Для отыскания промежутков выпуклости и вогнутости графика функции применяется вторая производная. Функция 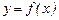будет выпукла на интервале(выпукла вверх) в том случае, если 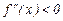на этом интервале, если же 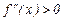на интервале (а, b ), то функция будет на интервале вогнутой( выпуклой вниз).

Когда в окрестности критической точки х₀второй производной (эти точки ищут из условий: 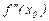не существует или 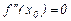) вторая производная функции меняет знак и существует касательная в точке 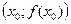_, то точка с координатами 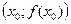называется точкой перегиба точка перегиба.

6. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график: С осью Оy: положив x =0, и найдя y = f (0). С осью Ох: положив y =0, и решив уравнение. f ( x )=0 ( это уравнение решают только в случае, если оно простое).

7.По результатам исследования по пунктам 1-6 построить график данной функции.

Пример:

Построить график функции .

1. Найдем область определения данной функции.

Данная функция определена и непрерывна на всей числовой оси, кроме точек х= -1 и х=1, т.к. в этих точках функция не определена. Значит точки х= -1 и х=1 - точки разрыва функции:

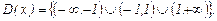
Исследуем данную функцию на четность, нечетность и периодичность.

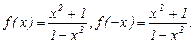
Так как f(-x)=f(x), то данная функция является четной и ее график симметричен относительно оси Оy. Поэтому дальнейшие исследования будем проводить для х 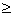0.

Функция не является периодической.

Исследуем характер точек разрыва функции и поведение функции в бесконечности.

В точках 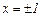имеем:

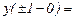
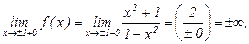
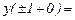
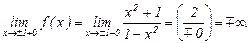
Значит, точки 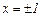– точки бесконечного разрыва 2 рода.

При 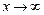получаем:

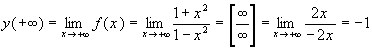Заметим, что при вычислении предела применялось правило Лопиталя):

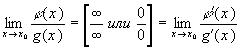
3. Найдем асимптоты графика функции.

а) Вертикальные.

Так как 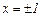- точки бесконечного разрыва функции, то 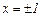– уравнения вертикальных асимптот графика функции .

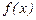б) Наклонные асимптоты ищем в виде .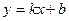

Для правой ветви графика функции имеем:

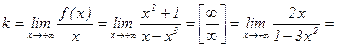
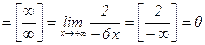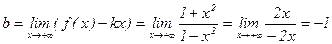
(при вычислениях пределов применялось правило Лопиталя).

Значит, y= -1 – уравнение горизонтальной асимптоты для правой ветви.

4. Найдем интервалы монотонности и экстремумы функции.

Вычислим первую производную функции:

Найдем теперь критические точки 1 рода из условий первая производная y'=0 или не существует.

y' существует для всех x принадлежащих D(x).

y'=0 при 4x= 0, т.е. x= 0 - критическая точка функции первого рода.

Отметим эту точку на числовой оси и разобьем область определения исследуемой функции ( х 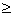0) на интервалы [0; 1) и (1; ):

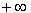Найдем знак y' на каждом из интервалов:

(0; 1): y'(0,5)=4·0,5/(1-0,5²)²=2/(0,75)²>0 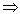функция возрастает на данном интервале.

(1; 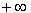): y'(2)=4·2/(1-2²)²=8/9>0 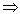функция возрастает на данном интервале.

Найдем интервалы выпуклости и вогнутости графика функции и точки перегиба.

Вычислим вторую производную функции:

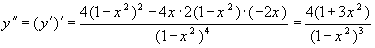
Найдем теперь критические точки 2 рода из условий y" не существует и y"=0.

y" существует для всех x принадлежащих D(x).

y"=0 при 3x²+1=0 - уравнение решений не имеет. Нет критических точек 2 рода.

Отметим на числовой оси область определения функции (х 0)

Найдем знак y^" на каждом из интервалов:

(0; 1): y^"(0,5)=4·(1+3·0,5²)/(1-0,5²)³=4·1,75/(0,75)³>0 направление выпуклости вниз на данном интервале.

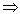(1; ): y^"(2)= 4·(1+3·4)/(1-4)³=4·13/(-27)<0 направление выпуклости вверх на данном интервале.

Точек перегиба нет.

6. Найдем точки пересечения с осями координат.

С осью 0у : х=0 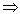y=1; т. пересечения – (0;1)

С осью 0х: у=0 при x² +1=0 – решений не имеет, нет точек пересечения.

7. По результатам исследования по пунктам 1-6 составим таблицу и построим график данной функции для х 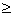0.

х	0	(0;1)	(1; )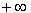
y'	0	+	+
y"		+	-
y	1	Выпукл. вниз возрастает	Выпукл. вверх возрастает
	min

Строим теперь график для х 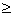0 и отражаем его симметрично относительно оси Оy

Задание 10. Нахождение частных производных ФМП и исследование на экстремум в замкнутой области.

Функции нескольких переменных: область определения, частные производные. Производные сложных функций

Определение: Функции двух переменных.

Если " упорядоченной паре чисел (x,y)ÎD по некоторому закону f ставится в соответствие число zÎE, то говорят, что задана функция z=f(x,y). Множество D- область определения, а E - область изменения функции.

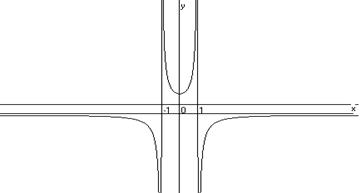
Геометрический смысл ФМП - поверхность в пространстве.

Пример:

Z=x²+y² задает параболоид, а Z=A₁x+B₁y+D₁ - плоскость.

Определение: Функции многих переменных (ФМП.)

Если "(x₁,x₂,...x_n) 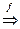zÎR, то говорят, что z=f(x₁,x₂,...x_n)- ФМП.

Пример:

Нахождение областей определения ФМП производят с учетом свойств элементарных функций.Если z=ln(xy) Þ xy>0 Û 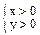или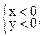

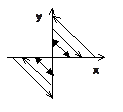
при z=ln(sin(xy)) Þ sin (xy)>0 Þ 0+2pk<xy<p+2pk.

Пределы ФМП

Определение:

Число А называют пределом ФМП z=f(x,y) в т.(x₀,y₀),если

"e>0 $d>0:"пар (x,y) из неравенства 0<(x-x₀)²+(y-y₀)²<d²

^{следует}Þ½f(x,y)-A½<e,

при этом пишут:

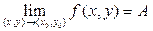Если А=0, т. е. 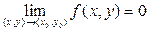, то функцию f(x,y) называют бесконечно-малой ( БМФ ) при (x,y)®(x₀,y₀).

Определение: Бесконечно большой функции.

Если "М>0 $d:"(x,y) из 0<(x- х₀)²+(y-y₀)²<d² Þ ½f(x,y)½>M, при этом пишут 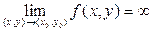и говорят, что z=f(x,y) бесконечно-большая ( ББФ), при (x,y)®(x₀,y₀).

Геометрический смысл.

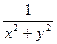
Определение: Непрерывной функции.

Говорят, что функция f(x,y) непрерывна в т. (х₀,y₀), если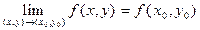

Замечание:

Кроме 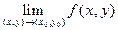существуют повторные пределы 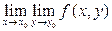и 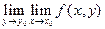, причем из 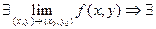- повторных пределов, но из $-я повторных пределов не следует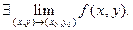

Пример:

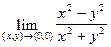-? Найдем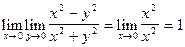

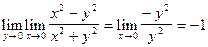
Но предел, если он существует, единственен, значит не существует предела z= , при (x,y)®(0,0).

Частные производные ФМП

Пусть z=f(x,y) определена в т. M₀(x₀,y₀) и ее окрестности

Назовем разность x-x₀=Dx- приращением координаты х, а

y-y₀=Dy- приращением координаты y , тогда для функции z=f(x,y) имеем

D_xz=f(x₀+Dx,y₀)-f(x₀,y₀)- частное приращение по координате x

D_yz=f(x₀,y₀+Dx)-f(x₀,y₀)- частное приращение по координате y.

Определение: Частной производной по переменной х.

Если существует конечный предел отношения D_xz к Dх при Dx®0, то он называется частной производной по переменной х и обозначается

Определение: Частной производной по переменной у.

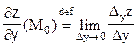При нахождении частной производной по заданной переменной фиксируются все переменные кроме заданной и частная производная находится как обычная производная функции одной переменной.

Геометрический смысл частных производных

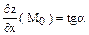
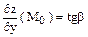
Пример:

z=x^y, 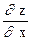=yx^y^-1, 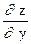=x^y×ln x

z=ln xy, z'_x=1/xy×(xy)'_x=y/xy=1/x.

z'_y=1/xy×(xy)'_y=x/xy=1/y.

Сложные ФМП

Определение:

Если z=f(x,y) определена на "(x,y)ÎD и имеют смысл функции x=x(u,v), y=y(u,v), "(u,v)ÎD, то говорят, что задана сложная ФМП z=f(x(u,v), y(u,v)).

Пример:

z=ln(cos(x×y)+tg(x+y))=ln (cosu+tgv), ,

При нахождении частных производных ФМП применяют следующие теоремы.

ЛИТЕРАТУРА

1. Шипачев В.С. Высшая математика. Учебник для вузов. М.: Высшая школа, 2005.

2. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-Пресс, 2005.

СОДЕРЖАНИЕ

1. Введение …………………………………………………………………… 3
2. Рекомендации по изучению теоретического материала …………... 4
3. Примеры решения задач ………………………………………………... 7
4. Расчетное задание ……………………………………………………… 39
Литература ………………………………………………………………… 62

Учебно-методическое издание

Денисов Валерий Николаевич

Бобков Владимир Иванович

Выборнова Елена Игоревна

Кулага Николай Филиппович

Математика.

Учебный практикум и контрольные задания

для студентов заочной формы обучения. 1 семестр

Технический редактор М.А. Андреев

Корректор Л.И. Чурлина

__________________________________________________________________________

Подписано в печать 14.10.2010 г.

Формат 60×84¹/₁₆. Тираж 70 экз. Печ. л. 4. Усл. печ. л. 3,72.

__________________________________________________________________________Издательский сектор филиала ГОУВПО «МЭИ (ТУ)» в г. Смоленске

214013 г. Смоленск, Энергетический проезд, 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

_____________________________________________________________

ФИЛИАЛ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)»

В г. Смоленске

В.Н. Денисов, В.И. Бобков,

Е.И. Выборнова, Н.Ф. Кулага

МАТЕМАТИКА

УЧЕБНЫЙ ПРАКТИКУМ

и контрольные задания

для студентов заочной формы обучения

Семестр

Смоленск 2010

УДК 51 (076)

М-34

Утверждено учебно-методическим Советом филиала ГОУВПО «МЭИ (ТУ)» в

г. Смоленске в качестве учебно-методического пособия для
студентов 1 курса заочной формы обучения

Рецензент:

Кандидат технических наук, доцент филиала ГОУВПО «МЭИ (ТУ)» в г. Смоленске
А.В. Борисов

П69

ВВЕДЕНИЕ

В других разделах пособия приведены примеры решениях типовых задач, задачи расчетного задания.

РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА

Программа курса для первого семестра обучения состоит из следующих разделов:

1. Матрицы, действия над ними. Алгебра матриц.

3. Обратная матрица, ee свойства. Ранг матрицы, его свойства. Матричные уравнения.

4. Системы линейных алгебраических уравнений. Правило Крамера. Теорема Кронеккера-Капелли.

5. Однородные системы. Структура общего решения неоднородной системы.

6. Таблица межотраслевого баланса, модель Леонтьева.

7. Собственные числа и собственные векторы квадратных матриц.

8. Векторы, действия над ними, базис, координаты. Линейная зависимость и независимость векторов.

9. Скалярное, векторное и смешанное произведения векторов.

12. Поверхности второго порядка. Канонические уравнения поверхностей второго порядка.

13. Понятие функции, способы задания функции. Понятие и определение предела функции в точке.

19. Функции нескольких переменных.

Изучение материала курса полезно проводить, придерживаясь тем и рекомендуемой литературы.

1. ТЕМА.

Матрицы, определители, системы линейных уравнений.

Литература:[1,2].

2. ТЕМА.

Литература:[1,2].

3. ТЕМА.

Литература:[1,2].

4. ТЕМА.

Литература:[1,2].

5. ТЕМА.

Функции нескольких переменных, их производные. Основные теоремы. Задачи на экстремум.

Литература:[1,2].

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задание 1. Даны матрицы

Найти определитель матрицы

Вычислить результирующую матрицу .

Образец решения задания.

Пусть

Вычислим определитель матрицы разложением по первой строке:

Произведем действия над матрицами с учетом свойств матриц

= .

После транспонирования матрицы имеем выражение

Перемножая матрицы, получим

Складывая соответствующие элементы двух полученных матриц, видим, что

Задание 2. Решить методом Гаусса и как матричное уравнение систему линейных уравнений.

Пример.

При решении систем методом исключения Гаусса вначале составим расширенную матрицу системы уравнений.

Шаг 1

= .

Шаг 2

Равносильные преобразования в методе Гаусса - это линейные комбинации строк матрицы.

Для иллюстрации метода Гаусса рассмотрим примеры.

Пример:

Решить систему уравнений:

Исключая неизвестные в 3 и 4 уравнениях по той же схеме завершим прямой ход метода Гаусса.

Используя обратный ход метода Гаусса, имеем:

А×Х = В Û А^-1×А×Х = А^-1×В Û Е×Х = А^-1×В,

т.е.

Х = А^-1×В

В том случае, когда матричное уравнение имеет вид A X×C = B , то схема решения такова:

А^-1×А× Х× C× C^-1= А^-1× В×C^-1 Û Х = А^-1× В×C^-1

Пример.

Задание 3. Треугольник ABC задан координатами его вершин: A(-2,1,3), B(1,-2,-3), C(2,-3,-1).

Найти

1). Площадь треугольника ABC;

2). Косинусы углов треугольника;

3). Высоту, опущенную из вершины А на сторону ВС;

4). Определить, параллелен ли вектор плоскости треугольника АВС.

Решение.

Углы треугольника легко определить, используя скалярное произведение векторов. Например, для угла А имеем:

Значит, вектор не параллелен плоскости треугольника АВС.

Задание 4. Задана прямая и плоскость

Найти

1). Угол между прямой и плоскостью в градусах, округлив результат до единиц градусов;

2). Точку пересечения прямой и плоскости, если она существует.

Решение.

Значит угол равен - .

Задание 5. Найти пределы функций.

При нахождении пределов функции пользуются следующими свойствами пределов и теоремами:

1).Предел константы равен самой константе.

k=k.

2). Если существует ($) f(x)=А (конечный), $ g(x)=B (конечный), то:

- предел суммы (разности) этих функций х®х₀ существует и равен сумме (разности) пределов

(f(x) g(x))= f(x) g(x);

- предел произведения существует и равен произведению пределов

[f(x)×g(x)]= f(x)× g(x);

- предел частного функций существует и равен частному пределов

, В¹0.

3). Пределы основных элементарных функций равны значениям этих функций в точке, где ищется предел.

Например

, , ,

При нахождении пределов нельзя пользоваться рассмотренными выше свойствами, если:

3) f(x)® +¥, j(x)® +¥, при x®x₀, то говорят, что имеет неопределенность вида .

4) f(x)® ¥, j(x)® ¥, при x®x₀, то говорят, что имеет неопределенность бесконечность делить на бесконечность.

Пример:

= = =

Пример:

Вычислить:

Порядок роста (наибольший показатель степени у слагаемых) числителя и знаменателя один и тот же и равен 11.

Делим числитель и знаменатель на и учитывая связь бесконечно больших и бесконечно малых функций, имеем:

Если и то существует
предел показательно-степенной функции, причем .

При этом если

1) 0<A<1;

2) A>1;

3) 0<A<1,

4) A>1,

Если же U®1, V®¥, при x®x₀, то говорят о неопределенности вида {1^¥}:

неопределенность.

Для раскрытия неопределенности такого вида применяется формула

Примеры:

Задание 6. Найти производную заданной функции.

Таблица производных:

Свойства производных.

Если существуют производные функций и в точках интервала , а и постоянные множители, то:

Пример:

2. Производная произведения вычисляется по формуле:

Пример:

3. Производная частного (дроби) вычисляется по формуле:

Пример:

Применяя таблицу производных и формулы для дифференцирования произведения и частного, получим

= =

= .

При нахождении производных часто применяется следующая теорема.

Теорема (о производной сложной функции).

Если функция дифференцируема для любых а функция дифференцируема для любых тогда сложная функция дифференцируема для любых и ее производная находится по формуле = .

Пример:

Найти производную сложной функции

, где .

В соответствии с теоремой имеем:

или

= = =

= = .

При нахождении производной, теорема может применяться несколько раз подряд.

Пример:

Для функции найти производную . Используя формулу из теоремы один раз имеем:

= .

Но функция тоже сложная. Применив теорему к этой функции, получим:

= .

Применяя теорему еще два раза, продолжим цепочку равенств

= = .

Таким образом, при дифференцировании сложной функции находится производная "внешней " функции без учета выражения, являющегося ее аргументом, затем полученная производная умножается на производную выражения, являющегося аргументом.

Для некоторых видов функций применяются специальные приемы нахождения производных.

Если имеется показательно- степенная функция или частное вида , где - функции,
- числа, то для нахождения производных этих функций применяется прием логарифмического дифференцирования. Этот прием основан на использовании основного логарифмического тождества , в частности, , и свойств логарифмов

Суть приема состоит в том, что производную любой функции можно найти как произведение этой функции на производную логарифма ее модуля

С учетом полученной формулы производная показательно-степенной функции равна произведению самой функции на производную логарифма этой функции:

или

Таким образом получена известная формула для производной показательно-степенной функции как сумма производных показательной (при фиксированной ) и степенной (при фиксированной ) функций.

Пример:

Пусть . Применяя прием логарифмического дифференцирования, имеем

Применяя прием логарифмического дифференцирования для случая дроби, имеем

= =

Пример:

Найти производную дроби

Применяя прием логарифмического дифференцирования и свойства логарифмов, видим, что

= =

= .

Преобразовав полученное выражение, получим:

Если у функции существовала производная в точке х₀ или на интервале то операция нахождения производной называлась дифференцированием функции. С наличием производной функции в точке тесно связано понятие дифференцируемости функции в точке, которое вводится по определению.

Определение:

Функция называется дифференцируемой в точке х₀, если ее приращение в окрестности этой точки представимо в виде

( ).

Здесь - некоторое число, определяемое в точке х₀. Используя дифференцируемость функции в точке, введем понятие дифференциала функции в точке.

Определение:

Дифференциалом функции в точке x₀ называется линейная часть приращения дифференцируемой функции, при этом вводится обозначение

Связь между наличием производной и дифференцируемостью функции в точке дается следующей теоремой.

Дата: 2018-12-21, просмотров: 261.

12 3 Следующая ⇒