1. Комплексные числа и действия над ними.

2. Функции комплексного переменного и их основные свойства.

3. Предел и непрерывность функции комплексного переменного. Дифферен-цируемость и аналитичность.

4. Интегрирование ФКП. Интегральные теоремы и формула Коши.

5. Степенные ряды в комплексной области. Ряды Тейлора и Лорана.

6. Особые точки и их классификация. Вычеты и их вычисление.

7. Теорема Коши о вычетах. Применение вычетов и вычисление интегралов.

Кратные интегралы

Задача об объеме цилиндрического бруса

Точно так же, как задача о площади криволинейной трапеции привела нас к понятию простого определенного интеграла, аналогичная задача об объеме цилиндрического бруса приведет нас к новому понятию – двойного интеграла.

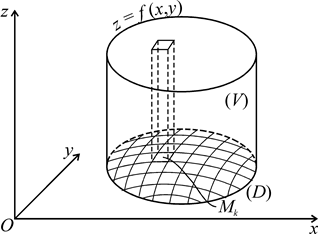
Рассмотрим тело (V), которое сверху ограничено поверхностью

                                                     z = f (x, y),                                 (1.1)

Рисунок 1.1

c боков – цилиндрической поверхностью с образующими, параллельными оси 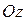, снизу – плоской фигурой  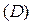на плоско-сти  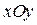(рис.1.1). Требуется найти объем  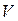тела.

Для решения этой задачи мы прибегнем к обычному в интегральном исчислении приему, состоящему в разложении искомой величины на элементарные части, приближенному подсчету каждой части, суммированию и последующему предельному переходу. С этой целью разобьем область 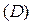 сетью кривых на части  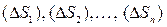и рассмотрим ряд цилиндрических столбиков, которые имеют своими основаниями эти частичные области и в совокупности составляют данное тело.

Для подсчета объема отдельных цилиндрических столбиков возьмем произвольно в каждой фигуре 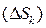 по точке M_k 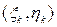. Если приближенно принять каждый столбик за цилиндр с высотой, равной аппликате 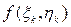, то объем отдельного столбика оказывается приближенно равным 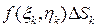, где 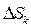 означает площадь фигуры 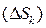. В таком случае приближенное выражение объема всего тела будет

.

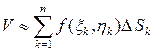Определение 1. Если взять любые пары точек в области то верхняя грань множества расстояний между ними называется диаметром области, обозначается d.

Для повышения точности этого равенства будем уменьшать размеры площадок 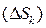, увеличивая их число. В пределе, при стремлении к нулю наибольшего из диаметров d всех областей 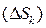, это равенство делается точным, так что

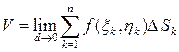,                          (1.2)

и поставленная задача решена.

Предел этого вида и есть двойной интеграл от функции f (x , y) по области ; он обозначается символом 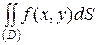 или 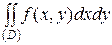, так что формула (1.2) для объема принимает вид

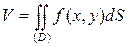.                                    (1.2^*)

Таким образом, двойной интеграл является прямым обобщением понятия простого определенного интеграла на случай функции двух переменных.