Полнофакторных экспериментов»

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ТЕОРИЯ ПЛАНИРОВАНИЯ МНОГОФАКТОРНЫХ

ЭКСПЕРИМЕНТОВ

Методические указания к лабораторным работам

Владимир 2010

УДК 621: 658.5.012.1

Рецензент

Доктор технических наук, профессор

А.В. Белевич

Печатается по решению редакционно-издательского совета Владимирского государственного университета

Гусев В.Г. Теория планирования многофакторных экспериментов : Метод. Указания к лаб. работам. – Владим. Гос. ун-т. Владимир, 2010, 110 с.

Составлены в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования. Приведено описание лабораторных работ по дисциплине «Теория планирования многофакторных экспериментов».

Включают цель, задания, теоретические сведения, методику выполнения и

требования к оформлению отчета.

Предназначены для магистров дневной формы обучения специальности

151001 – технология машиностроения.

Ил. Табл.

УДК 621: 658.5.012.1

Предисловие

В процессе разработки любого технического устройства (изделия) его создателям приходится решать множество научно-технических задач, различных по уровню сложности и объему, но преобладающим являются два направления: выбор наиболее правильного технического решения и его проектно-конструкторское «оформление» с определением оптимальных значений всех параметров и характеристик.

Сказанное в полной мере относится также к различного рода изучаемых явлений, технологических процессов машиностроения, и др. механических объектов и систем.

В настоящее время молодые специалисты, приходящие на работу в научно-производственные предприятия, занимающиеся созданием новой техники и технологии, недостаточно подготовлены к поиску новых технических решений и их использованию при разработке конкретной продукции.

Имея определенную подготовку по компьютерной технологии создания технических объектов, они часто не владеют методикой планирования многофакторных экспериментов, подготовкой, проведением экстремальных экспериментов, а также статистической обработкой данных проведенных опытов.

Отсутствие конкретных знаний и навыков в области оптимизации технических и технологических решений отражается непосредственно на научно-техническом уровне, а следовательно, на конечных результатах исследований и разработок.

Настоящие лабораторные работы направлены на теоретическую и практическую подготовку магистров в области планирования и реализации экстремальных многофакторных экспериментов, оптимизации многофакторных систем с наименьшими затратами живого и овеществленного труда.

Лабораторные работы служат для углубленного изучения лекционного материала по названной дисциплине и приобретения конкретных практических знаний в планировании, проведении многофакторных экспериментов с последующей оптимизацией параметров изучаемых многофакторных процессов и систем.

Лабораторная работа № 1

«Планирование и реализация линейных

Полнофакторных экспериментов»

Цель работы: изучение и освоение методики составления и практической реализации плана первого порядка полного факторного эксперимента.

Задание

1. Для условий точения детали типа вал на токарно-винторезном станке определить факторы, влияющие на шероховатость обработанной поверхности;

2. Определить основной, нижний и верхний уровни факторов, а также интервал варьирования;

3. Закодировать факторы и составить план полного факторного эксперимента и матрицу планирования;

4. Реализовать матрицу планирования, предварительно рандомизировав проведение опытов во времени;

5. Рассчитать коэффициенты регрессии и проверить их значимость;

6.Проверить гипотезу адекватности найденной линейной модели, связывающей средне-арифметическое отклонение профиля обработанной поверхности с независимыми факторами.

7. Построить графики зависимостей средне-арифметического отклонения профиля обработанной поверхности.

ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

При проведении однофакторного эксперимента варьируют один фактор, стабилизируя на выбранных уровнях все прочие факторы. Обработав результаты эксперимета, находят зависимость исследуемой величины только от одного фактора. Производя большое число однофакторных экспериментов при изучении многофакторной системы, получают частотные зависимости, представленные многими графиками, имеющими иллюстративный характер. Найденные таким образом частные зависимости невозможно объединить в одну общую модель процесса.

Использование однофакторного эксперимента для всестороннего исследования многофакторного процесса требует постановки очень большого числа опытов. Для их выполнения в ряде случаев необходимо значительное время, в течение которого влияние неконтролируемых факторов на результаты опытов может существенно измениться.

Отсюда следует, что результаты однофакторных экспериментов, полученные при исследовании многофакторных систем, малопригодны для практического использования. Кроме того, при решении экстремальных задач данные значительного числа опытов однофакторного эксперимента оказываются ненужными, так как получены они для области, далекой от оптимума.

Для изучения многофакторных систем наиболее целесообразным является применение статистических методов планирования эксперимента.

Под планированием эксперимента понимают определение числа и условий проведения опытов в многофакторном процессе, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

Планирование эксперимента – это новый раздел математической статистики. В нем всесторонне рассматриваются статистические методы планирования эксперимента. Эти методы позволяют во многих случаях при минимальном числе опытов получать модели многофакторных процессов.

Эффективность использования статистических методов планирования эксперимента при исследовании технологических процессов объясняется тем, что многие важные характеристики этих процессов являются случайными величинами, распределения которых близки к нормальному закону.

Характерными особенностями процесса планирования эксперимента являются стремление минимизировать число опытов; одновременное варьирование всех исследуемых факторов по специальным правилам – алгоритмам; применение математического аппарата, формализующего многие действия исследователя; выбор стратегии, позволяющей принимать обоснованные решения.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Эксперименты, которые ставят для решения задач оптимизации, называют экстремальными. Для решения экстремальной задачи необходимо иметь математическую модель исследуемого объекта. Математическая модель это система математических соотношений, описывающих изучаемый процесс или явление.

При планировании эксперимента под математической моделью понимают уравнение, связывающее параметр оптимизации с факторами. Такое уравнение называют также функцией отклика.

При постановке экстремальных экспериментов на первом этапе находят область оптимума. На втором этапе стремятся получить более полное представление о поверхности отклика в области оптимума. Решение экстремальной задачи предусматривает получение функции отклика и нахождение с помощью ее оптимальных условий протекания процесса.

В общем виде функция отклика , являющаяся и параметром оптимизации, может быть представлена выражением

, (1)

где – независимые переменные факторы.

Если функция отклика известна, то оптимальные условия процесса находят аналитически, без постановки эксперимента. Однако, часто приходится решать экстремальные задачи при неполном знании механизма процесса. В этом случае выборочную оценку функции отклика можно представить уравнением регрессии

(2)

где – коэффициенты регрессии при соответствующих переменных.

По результатам эксперимента можно определить только выборочные коэффициенты регрессии , которые являются оценками теоретических коэффициентов регрессии.

На первом этапе планирования эксперимента для определения направления движения к оптимуму и крутого восхождения по поверхности отклика функцию отклика выражают полиномом первой степени.

Метод Бокса-Уилсона предусматривает проведение опытов несколькими сериями и позволяет оптимизировать параметры процесса крутым восхождением по поверхности отклика. В каждой серии одновременно варьируют все факторы по определенным правилам. Опыты проводят так, чтобы после математической обработки результатов предыдущей серии можно было спланировать следующую серию опытов.

При планировании экстремального эксперимента цель исследования должна быть четко сформулирована и должна иметь количественную оценку.

Характеристику цели, заданную количественно, называют параметром оптимизации. Параметр оптимизации является реакцией, или откликом, на воздействие факторов, определяющих поведение процесса. Результаты эксперимента используют для получения математической модели исследуемого процесса.

Для определения коэффициентов линейного уравнения регрессии достаточно реализовать факторный эксперимент типа 2^к, где к — число факторов. Планы экспериментов типа 2 ^h называют планами первого порядка.

Крутое восхождение заканчивают после достижения области оптимума. Область оптимума чаще всего удается описать полиномом второй степени. Планы эксперимента, позволяющие оценить коэффициенты полинома второй степени, называют планами второго порядка.

Объект исследования. Для определения параметра оптимизации и выбора схемы планирования эксперимента предварительно изучают объект исследования на основе априорной информации, которую получают, изучая литературные данные и анализируя результаты ранее проведенных работ. При планировании эксперимента к объекту исследования предъявляют следующие требования.

1. Объект исследования должен удовлетворять требованию воспроизводимости. При многократном повторении опыта его результат имеет разброс значений, который характеризует воспроизводимость результата. Объект исследования удовлетворяет требованию воспроизводимости, если многократно повторенные опыты дают результаты с разбросом значений, не превышающим некоторой заданной величины.

2. Объект должен быть управляемым. На реальный объект действуют как управляемые, так и неуправляемые факторы. Последние влияют на воспроизводимость результатов эксперимента и могут служить причиной ее нарушения. Если требование воспроизводимости удовлетворяется, выявляют возможность проведения активного эксперимента, предусматривающего активное вмешательство в исследуемый процесс и выбирают для каждого опыта управляемые факторы на тех уровнях, которые представляют интерес для исследования.

Объект, на котором возможен активный эксперимент, называют управляемым.

Параметр оптимизации. При планировании эксперимента важно правильно выбрать параметр оптимизации. Движение к оптимуму возможно, если выбран один параметр оптимизации, а другие выступают в качестве ограничений. Возможно также построение обобщенного параметра как функции от множества исходных параметров. Параметр оптимизации должен быть количественным, доступным для измерения и должен выражаться одним числом.

Если измерение параметра невозможно, то пользуются ранговой оценкой. Ранг – это оценка параметра оптимизации по заранее выбранной шкале: двухбалльной, пятибалльной, десятибалльной и т. п. Ранговый параметр имеет ограниченную дискретную область определения. В простейшем случае область содержит два значения: да – нет; хорошо – плохо; брак – годные детали и т. д. При прочих равных условиях предпочтение необходимо отдавать количественному измерению, так как ранговая оценка носит субъективный характер.

Параметр оптимизации должен быть однозначным в статистическом смысле, т. е. заданному сочетанию уровней факторов должно соответствовать одно (с точностью до ошибки эксперимента) значение параметра оптимизации; эффективным в статистическом смысле, т. е. определяться с наибольшей точностью, что позволяет сократить до минимума число параллельных опытов; существовать для всех состояний исследуемого объекта; иметь физический смысл.

Параметры оптимизации могут быть экономическими, технико-экономическими, технико-технологическими и другими. Экономическими являются прибыль, себестоимость, рентабельность. К технико-экономическим относят производительность, надежность, долговечность.

Технико-технологическими параметрами являются механические, физические, физико-химические и некоторые другие характеристики изделия. Большинство параметров оптимизации прямо или косвенно связано с экономичностью производства или экономичностью эксплуатации изделия. Фактором называют независимую переменную величину, влияющую на параметр оптимизации.

Каждый фактор имеет область определения – совокупность всех значений, которые он может принимать. При исследовании процесса необходимо учитывать все существенные факторы. Если по каким-либо причинам влияние некоторых факторов невозможно учесть в эксперименте, то эти факторы должны быть стабилизированы на определенных уровнях в течение всего эксперимента.

Уровнем фактора называют численное значение фактора в эксперименте. Если число факторов велико, то необходимо отсеять те факторы, которые оказывают незначительное влияние на параметр оптимизации. Отсеивание несущественных факторов производят на основе априорного ранжирования или с помощью постановки отсеивающих экспериментов. Факторы должны быть:

1) управляемыми, т. е. позволяющими экспериментатору устанавливать их требуемые значения и поддерживать постоянными эти значения в течение опыта;

2) непосредственно воздействующими на объект исследования, так как трудно управлять фактором, который является функцией других факторов;

3) совместимыми, т. е. все комбинации уровней факторов) должны быть осуществимы и безопасны;

4) независимыми, т. е. позволяющими экспериментатору устанавливать требуемые уровни любого фактора независимо от уровней других факторов.

СОДЕРЖАНИЕ РАБОТЫ

1. На основании паспортных данных станка выписать ряды продольных подач суппорта станка и частот вращения шпинделя.

2. Назначить режимы резания для обработки заготовки, отдавая предпочтение тем элементам, которые в наибольшей степени влияют на шероховатость обработанной поверхности.

3. Выполнить обработку ступеней валика на различных режимах в соответствии с матрицей планирования многофакторного эксперимента.

4. Измерить шероховатость обработанных поверхностей.

5. Обработать результаты экспериментов:

- проверить значимость коэффициентов уравнения регрессии,

- проверить уравнение регрессии на адекватность,

-построить графики зависимостей шероховатости обработанной поверхности от выбранных значимых факторов.

РЕЗУЛЬТАТОВ ОПЫТОВ

После выбора плана эксперимента, основных уровней и интервалов варьирования факторов переходят к эксперименту. Каждая строка матрицы – это условия опыта. Для исключения систематических ошибок рекомендуется опыты, предусмотренные матрицей, проводить в случайной последовательности.

Порядок проведения опытов следует выбирать по таблице случайных чисел (табл. 3). Например, если требуется провести восемь опытов, то из случайного места таблицы последовательно выписывают числа, лежащие в интервале от 1 до 8, при этом отбрасывают уже выписанные числа больше восьми.

Так, например, начиная с числа 87 (1-я строка табл. 3), получаем следующую последовательность реализации опытов:

Номер опыта в матрице планирования

Порядок реализации опытов

1 2 3 4 5 6 7 8

7 2 8 3 1 4 5 6

Таблица 3

Фрагмент таблицы случайных чисел

87	63	88	23	62	51	07	69	59	02	89	49	14	98	53	41	92	36
07	76	85	37	84	37	47	32	25	21	15	08	82	34	57	57	35	22
03	33	48	84	37	37	29	38	37	89	76	25	09	69	44	61	88	23
13	01	59	47	64	04	99	59	96	20	30	87	31	33	69	45	58	48
00	83	48	94	44	08	67	79	41	61	41	15	60	11	88	83	24	82
24	07	78	61	89	42	58	88	22	16	13	24	40	09	00	65	46	38
61	12	90	62	41	11	59	85	18	42	61	29	88	76	34	21	80	78
27	84	05	99	85	75	67	80	05	57	05	71	70	21	31	92	99	06
96	53	99	25	13	63												_ —■—=-

Для компенсации влияния случайных погрешностей каждый опыт рекомендуется повторить п раз.

ОФОРМЛЕНИЕ ОТЧЕТА И СДАЧА ЗАЧЕТА

ПО ЛАБОРАТОРНОЙ РАБОТЕ

После выполнения лабораторной работы студент оформляет отчет, в котором приводятся кратко теоретические положения, матрица планирования полного факторного эксперимента первого порядка, заполненная с учетом результатов проведенных опытов и результатов измерения шероховатости шлифованных поверхностей.

В отчете приводятся расчеты, на основании которых получена многофакторная линейная модель.

Приводится проверка значимости коэффициентов уравнения регрессии и адекватности модели, а также графики зависимостей, связывающих параметр оптимизации с независимыми факторами. Отчет студента по лабораторной работе состоит в правильных ответах студента на вопросы преподавателя, касающихся как методики планирования, постановки и проведения экспериментов, их статистической обработки, так и объяснения физической сущности влияния того или иного фактора на параметр оптимизации.

Лабораторная работа № 2

«Планирование и реализация линейных

Задание

1. Для условий плоского шлифования детали на плоскошлифовальном станке определить факторы, влияющие на волнистость обработанной поверхности;

2. Определить основной, нижний и верхний уровни факторов, а также интервал варьирования;

3. Закодировать факторы и составить план дробного факторного эксперимента и матрицу планирования;

4. Реализовать матрицу планирования, предварительно рандомизировав проведение экспериментов во времени;

5. Рассчитать коэффициенты регрессии и проверить их значимость;

6. Проверить гипотезу адекватности найденной линейной модели, связывающей волнистость обработанной поверхности с независимыми факторами.

7. Построить графики зависимостей волнистости обработанной поверхности от независимых факторов.

ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

При большом числе факторов (к>3) проведение полного факторного эксперимента связано с большим числом опытов, значительно превосходящим число коэффициентов линейной модели. Если при получении модели можно ограничиться линейным приближением, т. е. получить адекватную модель в виде полинома 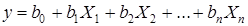, то число опытов можно резко сократить в результате применения дробного факторного эксперимента.

Таблица 1

Матрица планирования

Номер опыта	X₀	X₁	Х₂	Х₃(X₁ Х₂)	Y
1	+	+	+	+	Y₁
2	+	–	+	–	Y₂
3	+	+	–	–	Y₃
4	+	–	–	+	Y₄

Так, например, в полном факторном эксперименте типа 2² при линейном приближении коэффициент регрессии b ₁₂ можно принять равным нулю, а столбец X₁ Х₂ матрицы (табл. 1) использовать для третьего фактора Х₃.

В этом случае линейная модель будет выражаться уравнением 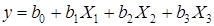. Для определения коэффициентов этого уравнения достаточно провести четыре опыта вместо восьми в полном факторном эксперименте типа 2³.

План эксперимента, предусматривающий реализацию половины опытов полного факторного эксперимента, называют полурепликой. При увеличении числа факторов (к>3) возможно применение реплик большей дробности.

Дробной репликой называют план эксперимента, являющийся частью плана полного факторного эксперимента. Дробные реплики обозначают выражением 2 ^k ^-р , где р – число линейных эффектов, приравненных к эффектам взаимодействия. При р = 1 получают полуреплику; при р = 2 получают 1/4-реплику; при р = 3 получают 1/8-реплику и т. д. по степеням двойки.

Так, например, если в полном факторном эксперименте 2³ (табл. 2) один из эффектов взаимодействия (Х₁Х₂, Х₁Х_З, Х₂Х_З, Х₁Х₂Х_З) заменим четвертым фактором Х₄ то получим полуреплику 2^4-1 от полно факторного эксперимента 2⁴. Если два эффекта взаимодействия заменить факторами Х₄ и Х₅, то получим 1/4 – реплику 2^5-2 от полного факторного эксперимента 2⁵. Можно получить 1/8 – реплику от полного факторного эксперимента, заменив три эффекта взаимодействия факторами Х₄, Х₅ и Х₆.

Таблица 2

Матрица полного факторного эксперимента типа 2³

Номер опыта	X₀	X₁	Х₂	Х₃	X₁ Х₂	X₁ Х₃	X₂ Х₃	X₁ Х₂ Х₃	Y_i
1	+	–	–	+	+	–	–	+	Y₁
2	+	+	–	+	–	+	–	–	Y₂
3	+	–	+	+	–	–	+	–	Y₃
4	+	+	+	+	+	+	+	+	Y₄
5	+	–	–	–	+	+	+	–	Y₅
6	+	+	–	–	–	–	+	+	Y₆
7	+	–	+	–	–	+	–	+	Y₇
8	+	+	+	–	+	–	–	–	Y₈

Если заменить четыре эффекта взаимодействия факторами Х₄, Х₅ и Х₆и Х₇, то получим 1/16 – реплику 2^7-4 от полного факторного эксперимента 2⁷. Реплики, которые используют для сокращения числа опытов в 2^m раз, где т = 1, 2, 3, ..., называют регулярными.

В связи с тем, что в дробных репликах часть взаимодействий заменена новыми факторами, то найденные коэффициенты уравнения регрессии будут являться совместными оценками линейных эффектов и эффектов взаимодействия.

Коэффициенты 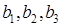будут оценками совмещенных эффектов, а именно

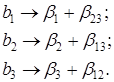
Коэффициент b ₁ является оценкой влияния фактора X₁ и парного взаимодействия X₂X₃ на функцию отклика. Влияние фактора X₁ в этом случае характеризуется величиной 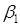, а влияние взаимодействия – величиной 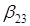. Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.

СОДЕРЖАНИЕ РАБОТЫ

1. На основании паспортных данных станка выписать ряды продольных, поперечных подач стола станка и частот вращения шпинделя.

2.Выбрать факторы, влияющие на волнистость шлифованной поверхности, определить их верхний, нижний уровни и интервалы варьирования.

3.Выбрать план дробного факторного эксперимента, генерирующее соотношение и составить матрицу планирования.

4.Назначить режимы резания и выполнить обработку плоскостей детали на различных режимах.

5. Измерить волнистость обработанных поверхностей.

6. Обработать результаты экспериментов.

7. Проверить значимость коэффициентов уравнения регрессии.

8. Проверить уравнение регрессии на адекватность.

9. Построить графики зависимостей волнистости обработанной поверхности от независимых факторов.

РЕЗУЛЬТАТОВ ОПЫТОВ

После выбора плана эксперимента, основных уровней и интервалов варьирования факторов переходят к эксперименту. Каждая строка матрицы — это условия опыта. Для исключения систематических ошибок рекомендуется опыты, предусмотренные матрицей, проводить в случайной последовательности. Последовательность проведения опытов следует выбирать по таблице случайных чисел (табл.3). Например, если требуется провести восемь опытов, то из случайного места таблицы последовательно выписывают числа, лежащие в интервале от 1 до 8, при этом отбрасывают уже выписанные числа и числа больше восьми. Для компенсации влияния случайных погрешностей каждый опыт рекомендуется повторить п раз. Опыты, повторенные несколько раз при одних и тех же значениях факторов, называют параллельными. В дальнейшем обработку экспериментальных данных следует проводить аналогично обработке данных в лабораторной работе № 1.

ОФОРМЛЕНИЕ ОТЧЕТА И СДАЧА ЗАЧЕТА

ПО ЛАБОРАТОРНОЙ РАБОТЕ

После выполнения лабораторной работы студент оформляет отчет, в котором приводятся кратко теоретические положения, матрица планирования первого порядка, заполненная с учетом результатов проведенных экспериментов и результатов измерения шероховатости шлифованных поверхностей. В отчете приводятся расчеты, на основании которых получена многофакторная модель.

Отчет студента по лабораторной работе состоит в правильных ответах студента на вопросы преподавателя, касающихся как методики планирования, постановки и проведения экспериментов, их статистической обработки, так и объяснения физической сущности влияния того или иного фактора на параметр оптимизации.

Лабораторная работа № 3

«Планирование и реализация центрального

Задание

1. На основании результатов обработки данных и получения неадекватной линейной многофакторной модели разработать матрицу центрального композиционного рототабельного многофакторного эксперимента второго порядка.

2. Реализовать матрицу планирования второго порядка, предварительно рандомизировав проведение опытов во времени;

3. Рассчитать коэффициенты регрессии и проверить их значимость;

4. Проверить гипотезу адекватности найденной модели второго порядка, связывающей параметр оптимизации с независимыми факторами_;

5. Построить графики зависимостей параметра оптимизации от независимых факторов.

ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

В процессе реализации центрального композиционного ортогонального плана функцию отклика в области оптимума обычно удается аппроксимировать полиномом второй степени вида

Для оценки всех коэффициентов полинома второй степени необходимо, чтобы в плане эксперимента каждый фактор принимал не менее трех значений. Применение планов типа 3^k связано с большим числом опытов. Более рациональным является центральное композиционное планирование.

Центральный композиционный план второго порядка получают достройкой некоторого количества точек к «ядру», образованному линейным планом. При числе к факторов менее пяти за «ядро» центрального композиционного плана обычно принимают план полного факторного эксперимента типа 2 ^k .

Если число факторов более пяти, то за «ядро» центрального композиционного плана принимают полуреплику от полного факторного эксперимента. Такой выбор «ядра» центрального композиционного плана обусловлен тем, что от «ядра» плана требуется раздельная оценка всех линейных эффектов и парных эффектов взаимодействия.

Для двух факторов центральный композиционный план второго порядка может быть представлен следующей схемой (рис. 1).

К полному факторному эксперименту 2² (точки 1, 2, 3, 4) добавляют некоторое число n₀ опытов в центре плана (точка 9) и четыре «звездных» точки 5, 6,7,8 с координатами ( + ; 0); (– ; 0); (0, + ); (0;– ).

План второго порядка для двух факторов может быть представлен матрицей (табл.1).

Чтобы получить центральный композиционный план второго порядка для трех факторов, к полному факторному эксперименту 2³ добавляют шесть «звездных» точек с координатами ( + ; 0; 0); (– ; 0; 0); (0; + ; 0); (0; – ; 0); (0; 0; + ); (0; 0; – ) и некоторое число n₀ точек в центре плана.

Центральный композиционный план второго порядка для трех факторов может быть выражен матрицей (табл. 2).

Рис. 1. Схема центрального композиционного плана второго порядка

для двух факторов

Таблица 1

Матрица центрального композиционного плана второго порядка

для двух факторов

Содержание плана	Номер опыта	X₀	X₁	Х₂	X₁ Х₂	X₁²	Х₂²	Y
План Типа 2²	1	+	+	+	+	+	+	Y₁
	2	+	-	⁺	-	+	+	Y₂
	3	+	+	–	-	+	+	Y₃
	4	⁺	-	–	+	+	+	Y₄
«Звездные» точки	5	₊	+	0	0		0	Y₅
	6	+		0	0		0	Y₆
	7	+	0	+	0	0		Y₇
	8	+	0		0	0		Y₈
Нулевая точка	9	+	0	0	0	0	0	Y₉

Таблица 2

Матрица центрального композиционного плана второго порядка

для трех факторов

Содержа-ние плана	Номер опыта	X₀	X₁	Х₂	Х₃	X₁ Х₂	X₁ Х₃	X₂ Х₃	X₁²	Х₂²	Х₃²	Y
План Типа 2²	1	+	+	+	+	+	+	+	+	+	+	Y₁
	2	+	-	+	+	–	-	+	+	+	+	Y₂
	3	+	+	-	+	–	+	–	+	+	+	Y₃
	4	+	-	-	+	+	-	–	+	+	+	Y₄
	5	+	+	+	–	+	-	–	+	+	+	Y₅
	6	+	-	+	–	–	+	–	+	+	+	Y₆
	7	+	+	-	–	–	-	+	+	+	+	Y₇
	8	+	-	-	–	+	+	+	+	+	+	Y₈
«Звездные» точки	9	+		0	0	0	0	0		0	0	Y₉
	10	+		0	0	0	0	0		0	0	Y₁₀
	11	+	0		0	0	0	0	0		0	Y₁₁
	12	+	0		0	0	0	0	0		0	Y₁₂
	13	+	0	0		0	0	0	0	0		Y₁₃
	14	+	0	0		0	0	0	0	0		Y₁₄
Нулевая точка	15	+	0	0	0	0	0	0	0	0	0	Y₁₅

Общее число N опытов центрального композиционного план; зависит от числа k факторов и определяется по выражению .

Величину «звездного» плеча и число опытов n₀ в центре плана выбирают в зависимости от принятого критерия оптимальности. За критерий оптимальности обычно принимают ортогональность или ротатабельность плана.

Ортогонализация планов достигается выбором «звездного» плеча . Значения «звездного» плеча , вычисленные для различного числа факторов, приведены в табл. 3.

Если ортогональность принять за достаточный критерий оптимальности плана эксперимента, то на число опытов в центре плана не накладывается какого-либо ограничения.

Таблица 3

Величина «звездного» плеча

Число независимых переменных	Ядро плана	Число дополнительных опытов	Величина плеча
2	2²	5	1,000
3	2³	7	1,215
4	2⁴	9	1,414
5	2^5-1	11	1,547

Ортогональный центральный композиционный план второго порядка для двух факторов может быть представлен матрицей (табл. 4).

Таблица 4

Ортогональный центральный композиционный план второго порядка

для двух факторов

Содержание плана	Номер операции	X₀	X₁	Х₂	X₁ Х₂	X₁²-2/3	Х₂²-2/3	Y
План типа 2²	1	+	+	+	+	+ 1/3	+ 1/3	Y₁
	2	+	-	+	–	+ 1/3	+ 1/3	Y₂
	3	+	+	–	–	+ 1/3	+ 1/3	Y₃
	4	+	–	–	+	+ 1/3	+ 1/3	Y₄
«Звездные» точки с плечом	5	+	+	0	0	+ 1/3	– 2/3	Y₅
	6	+	–	0	0	+ 1/3	– 2/3	Y₆
	7	+	0	+	0	– 2/3	+ 1/3	Y₇
	8	+	0	–	0	– 2/3	+ 1/3	Y₈
Нулевая точка	9	⁺	0	0	0	– 2/3	– 2/3	Y₉

2. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТОВ И ОБРАБОТКА

РЕЗУЛЬТАТОВ ОПЫТОВ

Для получения модели второй степени, связывающей параметр оптимизации с независимыми факторами, необходимо провести дополнительные к плану первого порядка опыты согласно матрице планирования, представленной в табл.4 (приведенная матрица соответствует двум факторам, в случае числа факторов больше двух необходимо составить новую матрицу планирования).

Обработку экспериментальных данных проводим, с учетом результатов опытов в звездных точках факторов.

Благодаря ортогональности матрицы планирования коэффициенты регрессии определяются независимо друг от друга по формуле

где i – номер столбца матрицы; j – номер опыта; X_ij – элементы соответствующего столбца матрицы; Y_i – значение параметра оптимизации в i-м опыте.

Дисперсии коэффициентов регрессии определяются по формуле

Дисперсии коэффициентов не равны, так как суммы квадратов элементов столбцов матрицы

не равны друг другу.

Реализация опытов по матрице планирования с квадратичной переменной позволяет построить модель вида

Неизвестный коэффициент b₀ находят по выражению

с дисперсией

Проверка адекватности уравнения второго порядка, полученного после центрального композиционного ортогонального планирования, производится так же, как и проверка адекватности линейной модели, полученной при реализации плана первого порядка.

СОДЕРЖАНИЕ РАБОТЫ

1. По данным матрицы центрального композиционного ортогонального планирования второго порядка назначить режимы резания для обработки заготовки.

2. Выполнить обработку плоскостей деталей на уровнях, соответствующих звездным точкам и основному уровням факторов.

3. Измерить волнистость обработанных поверхностей.

4. Обработать результаты экспериментов.

5. Проверить значимость коэффициентов уравнения регрессии.

6. Проверить уравнение регрессии на адекватность.

7. Построить графики зависимостей волнистости обработанной поверхности от независимых факторов.

ОФОРМЛЕНИЕ ОТЧЕТА И СДАЧА ЗАЧЕТА

ПО ЛАБОРАТОРНОЙ РАБОТЕ

После выполнения всех пунктов раздела 6 студент оформляет отчет по лабораторной работе, в котором приводятся кратко теоретические положения, матрица центрального композиционного планирования второго порядка, заполненная с учетом результатов проведенных экспериментов и результатов измерения волнистости шлифованных поверхностей. В отчете приводятся расчеты, на основании которых получена многофакторная модель второго порядка.

Приводится проверка значимости коэффициентов уравнения регрессии и адекватности модели второго порядка, а также графики зависимостей, связывающих параметр оптимизации с независимыми факторами.

Лабораторная работа № 4

«Оптимизация параметров методом крутого восхождения по поверхности отклика»

Цель работы: изучение и освоение методики отыскания оптимума функции, полученной в результате практической реализации плана первого или второго порядка и адекватно описывающей изучаемый процесс.

Задание

1. Для полученного в результате выполнения лабораторных работ №№1-3 уравнения регрессии, связывающего исследуемый параметр с независимыми факторами, найти оптимальное значения функции отклика.

2. Изучить методику расчета шага каждого фактора при крутом восхождении по поверхности отклика,

3. Выполнить крутое восхождение по поверхности отклика и добиться оптимального значения исследуемого параметра.

4. Построить графики зависимостей оптимального параметра обработанной поверхности от независимых факторов для адекватной линейной модели или модели второго порядка.

ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Под математической моделью понимают вид функции отклика 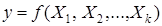. Выбор модели зависит от задачи исследования и от предъявляемых требований к модели.

Экстремальные задачи часто решают, используя шаговый метод. В этом случае модель должна удовлетворять требованиям этого метода.

В основе шагового метода лежит предположение, что совокупность значений параметра оптимизации у, полученная при различных сочетаниях значений факторов X_i, образует поверхность отклика.

Для наглядности представления о поверхности отклика при наличии Y_max рассмотрим простейший случай, при котором число факторов равно двум (X ₁ и Х₂).

Для каждого фактора установлены два значения: максимальное и минимальное. Между этими значениями каждый фактор может изменяться непрерывно или дискретно.

Границы значений факторов образуют на плоскости Х 1 0Х 2 (рис. 1), прямоугольник ABCD , внутри которого лежат точки возможных значений X ₁ и Х₂.

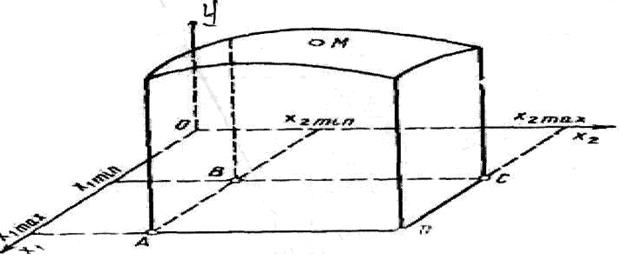Рис. 1. Поверхность отклика

Если по оси у откладывать значения Y_i полученные при различных сочетаниях значений факторов, то точки Y_i будут лежать .на поверхности отклика.

На этой поверхности будет находиться точка М, соответствующая оптимальному значению у. Для нахождения этой точки необходимо шаг за шагом двигаться по поверхности отклика.

Шаговый метод исходит из предположения, что поверхность отклика является гладкой и имеет единственный оптимум. Поверхность отклика расположена в k +1–мерном пространстве, которое называют факторным.

Факторное пространство зависит от числа k факторов. При большом числе факторов это пространство является многомерным, и геометрическая интерпретация функции отклика становится невозможной.

Для описания в многомерном пространстве поверхности отклика пользуются языком алгебры. Гладкость поверхности отклика и наличие на ней одной точки оптимума позволяют двигаться к последней в любом направлении, независимо от исходной точки.

При шаговом методе каждому фактору придают два значения: максимальное и минимальное. Эти значения составляют только часть возможных значений факторов.

На первом этапе реализации шагового метода выбирается лишь какая-то подобласть из области возможных значений факторов, и в этой подобласти ставится эксперимент.

На основании результатов этого эксперимента строится первая модель, по которой предсказываются отклики для значений факторов, выходящих за пределы выбранной подобласти.

Чем дальше от этой подобласти лежит точка, определяющая значения факторов, тем с меньшей точностью путем экстраполяции можно предсказать значение отклика для этой точки. Поэтому экстраполяцию производят вблизи подобласти эксперимента и используют ее для выбора условий проведения следующего эксперимента, т. е. устанавливают новые интервалы значений факторов или выбирают новую подобласть факторного пространства.

Поставив новый эксперимент, строят вторую модель и на основании ее делают следующий шаг в направлении к оптимуму. В этом и заключается сущность шагового метода.

Исходя из сущности этого метода к модели предъявляется главное требование, заключающееся в способности модели «предсказывать» направление дальнейших опытов с требуемой точностью. Это означает, что предсказанные по модели значения отклика должны отличаться от фактических не более, чем на некоторую наперед заданную величину.

Модель, удовлетворяющую этому требованию, называют адекватной. Если имеется несколько удовлетворяющих

указанному требованию моделей, то из них выбирается наиболее простая. Наиболее простой моделью является полином. Полином линеен относительно неизвестных коэффициентов, что упрощает обработку наблюдений.

Полином может быть первой, второй и более высокой степени, коэффициенты полинома вычисляют по результатам опытов. Чем больше число коэффициентов в полиноме, тем большее количество опытов необходимо поставить для их определения. Число коэффициентов зависит от степени полинома: чем выше степень, тем больше число коэффициентов. На первом этапе планирования – определении направления движения к оптимуму и крутого восхождения по поверхности отклика – наиболее целесообразно неизвестную функцию отклика аппроксимировать полиномом первой степени. Аппроксимация – это замена одной функции другой функцией, в каком-то смысле эквивалентной первой.

Полином первой степени имеет минимальное число коэффициентов при данном числе факторов и содержит необходимую информацию о направлении градиента, под которым понимают направление наискорейшего улучшения параметра оптимизации.

После достижения путем постепенного перемещения по поверхности отклика подобласти, в которой лежит точка оптимума, иногда для более полного описания подобласти переходят от полинома первой степени к полиному второй степени.

Движение по градиенту обеспечивает наиболее короткий путь к оптимуму, так как направление градиента – это направление самого крутого склона, ведущего от данной точки к вершине. Если изменять факторы пропорционально их коэффициентам с учетом знака, то движение к оптимуму будет осуществляться по самому крутому пути.

Этот процесс движения к области оптимума называют крутым восхождением. Технику расчета крутого восхождения рассмотрим на примере задачи с одним фактором X ₁ (рис.2). Предположим, что кривая 1 представляет собой неизвестную функцию отклика. В результате реализации плана эксперимента с центром в точке О получено уравнение регрессии 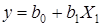адекватно описывающее функцию отклика в области значений фактора X ₁ от –1 до +1.

Значение коэффициента регрессии 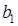равно тангенсу угла между линией регрессии и осью данного фактора. Если шаг движения по оси x ₁ принять равным 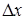, то, умножив его на 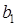, получим координаты ( 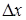и 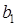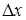) точки А, лежащей на градиенте.

После второго шага расстояние по оси x ₁ будет равно 2 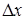. Умножив 2 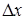на 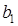, найдем координаты 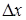2 ; и 2 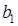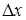точки В, лежащей на градиенте, и т. д. Затем проводят опыты с условиями, отвечающими точкам на градиенте. По результатам этих опытов определяют область оптимума.

В практических задачах для сокращения объема эксперимента проводят не все, а только часть опытов, предусмотренных крутым восхождением. Условия опытов выбирают так, чтобы область оптимума можно было заключить в «вилку». После этого опыты проводят в точках интервала, образованного точками «вилки», до нахождения наилучшего результата.

Рис.2 Схема к расчету координат точек в направлении градиента: 1-график функции отклика; прямая направления градиента.

В случае k факторов расчет крутого восхождения по оси каждого фактора производят аналогичным образом, так как коэффициенты b_i определяются независимо друг от друга.

При этом движение по осям осуществляют одновременно.

Шаг движения по градиенту выбирают таким, чтобы его минимальная величина была больше ошибки, с которой фиксируют фактор. Максимальную величину шага ограничивает область определения фактора.

Необходимо учитывать, что при движении к оптимуму малый шаг потребу значительного числа опытов, а большой шаг может привести к проскоку области оптимума.

Шаг движения выбирают для одного фактора, а для остальных его рассчитывают по выражению

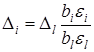
где – выбранный шаг движения для фактора l; 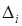– шаг движения дл: i-го фактора; 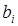, 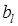– коэффициенты регрессии i-го и l-го факторов; 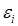, 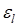– интервалы варьирования i-го и l-го факторов.

Движение по градиенту должно начинаться от нулевой точки основного уровня каждого фактора, так как коэффициенты регрессии вычислены дл. функции отклика, разложенной в ряд Тейлора в окрестности нулевой точки.

Если коэффициенты регрессии значительно отличаются друг от друга, то рекомендуют изменить интервалы варьирования факторов и провести новую серию опытов, ибо при различии коэффициентов на порядок и боле! многофакторный эксперимент при крутом восхождении может превратиться однофакторный.

Рассчитав шаг движения для каждого фактора, находят условия: «мысленных» опытов. «Мысленными» называют опыты, условия, проведения которых на стадии крутого восхождения установлены с учетом шаг; движения для каждого фактора.

С целью проверки результатов крутого восхождения часть мысленных опытов реализуется.

Если при движении к оптимуму возникает ситуация, препятствующая изменению каких-либо факторов, то эти факторы можно фиксировать на оптимальных уровнях, продолжая движение по стальным факторам.

Крутое восхождение прекращается, если найдены условия оптимизации или если ограничения на факторы делают дальнейшее движение по градиент неразумным.

Рассмотренный метод крутого восхождения в область оптимума носит название метода Бокса – Уилсона.

2.СОДЕРЖАНИЕ РАБОТЫ

1. По полученной ранее адекватной модели найти экстремальное значение параметра оптимизации.

2. Выбрать фактор, наиболее существенно влияющий на параметр оптимизации, и назначить шаг, с которым он будет изменяться фактор при крутом восхождении по поверхности отклика.

3. Рассчитать шаг движения по градиенту для остальных факторов.

4. Рассчитать факторы для мысленных и реализованных опытов при крутом восхождении в область оптимума.

Для выполнения пунктов 3 и 4 удобно пользоваться примером – таблицей.

Таблица

Расчет крутого восхождения

Наименование	X₁	Х₂	X₃	y
Основной уровень	0,40	840	60	–
Коэффициент	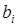20	11,9	–5.1	–
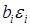
	0,15	100	60	–
Интервал варьирования	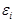3	1190	–306	–
Шаг	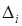0,0252	10	–2,57	–
Округленный шаг	0,03	10	–3	–
Мысленный опыт	0,43	850	57	–
То же	0,46	860	54	–
Реализованный опыт	0,49	870	51	108
Мысленный опыт	0,52	880	48	–
То же	0,55	890	45	–
Реализованный опыт	0,58	900	42	196
Реализованный опыт	0,61	910	39	366
Реализованный опыт	0,64	920	36	313

Как следует из таблицы лучший результат (оптимальное значение параметра у) получен в предпоследнем опыте. Величина параметра оптимизации достигла своего максимального значения у =366, на этом работа была закончена, так как цель многофакторного эксперимента достигнута.

ОФОРМЛЕНИЕ ОТЧЕТА И СДАЧА ЗАЧЕТА

ПО ЛАБОРАТОРНОЙ РАБОТЕ

После выполнения всех пунктов раздела 4 студент оформляет отчет по лабораторной работе, в котором приводятся кратко теоретические положения, расчеты шагов факторов при кругом восхождении по поверхности отклика. Рассчитываются значения факторов, как в мысленных, так и реализуемых опытах.

Отчет студента по лабораторной работе состоит в правильных ответах студента на вопросы преподавателя, касающихся как методики крутого восхождения по поверхности отклика, так и проведения экспериментов, их статистической обработки, а также объяснения физической сущности влияния того или иного фактора на значение параметра оптимизации.

Оглавление

1 .Предисловие...................................................................................... ...…3

2.Лабораторная работа №1. Планирование и реализация линейных полнофакторных экспериментов................................................................. …...4

3.Лабораторная работа №2. Планирование и реализация линейных дробных факторных экспериментов......................................................................... ……19

4.Лабораторная работа №3. Планирование и реализация центрального композиционного рототабельного многофакторного эксперимента второго порядка..................................................................................................................... …...26

5.Лабораторная работа №4. Оптимизация параметров методом крутого восхождения по поверхности отклика…………………………………………….32

ТЕОРИЯ ПЛАНИРОВАНИЯ МНОГОФАКТОРНЫХ

ЭКСПЕРИМЕНТОВ

Методические указания к лабораторным работам

Владимир 2010

УДК 621: 658.5.012.1

Рецензент

Доктор технических наук, профессор

А.В. Белевич

Печатается по решению редакционно-издательского совета Владимирского государственного университета

Включают цель, задания, теоретические сведения, методику выполнения и

требования к оформлению отчета.

Предназначены для магистров дневной формы обучения специальности

151001 – технология машиностроения.

Ил. Табл.

УДК 621: 658.5.012.1

Предисловие

Лабораторная работа № 1

«Планирование и реализация линейных

полнофакторных экспериментов»

Задание

2. Определить основной, нижний и верхний уровни факторов, а также интервал варьирования;

3. Закодировать факторы и составить план полного факторного эксперимента и матрицу планирования;

4. Реализовать матрицу планирования, предварительно рандомизировав проведение опытов во времени;

5. Рассчитать коэффициенты регрессии и проверить их значимость;

7. Построить графики зависимостей средне-арифметического отклонения профиля обработанной поверхности.

ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В общем виде функция отклика , являющаяся и параметром оптимизации, может быть представлена выражением

, (1)

где – независимые переменные факторы.

(2)

где – коэффициенты регрессии при соответствующих переменных.

Объект, на котором возможен активный эксперимент, называют управляемым.

3) совместимыми, т. е. все комбинации уровней факторов) должны быть осуществимы и безопасны;

Дата: 2018-12-21, просмотров: 247.

12 3 4 5 6 7 Следующая ⇒