Курса всех форм обучения по направлениям
подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
(Часть II )
ОРЕЛ
Издательство ОрелГИЭТ
2012
УДК 53
ББК 22.3
Ф 912
Подготовлено на кафедре математики и естествознания
Рекомендовано Методическим советом инженерно-технологического
факультета
Рецензент: кандидат технических наук, доцент Орловского государственного института экономики и торговли Глазова Г.В.
Фролов М.А., Ашихина Л.А. Лабораторный практикум по дисциплине «Физика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавров: 100800.62 «Товароведение», 260800.62 «Технология продукции и
организация общественного питания» (Часть II). – Орёл: Издательство ОрелГИЭТ, 2012. - 36 с.,
Пособие содержит учебный материал по второй части цикла лабораторных работ по механике, молекулярной физике и термодинамике. Приведены сведения по технике безопасности при выполнении лабораторных работ, контрольные вопросы для самопроверки по каждой лабораторной работе.
Материал данного пособия рекомендуется к использованию при изучении дисциплины «Физика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавриата.100800.62 «Товароведение» и 260800.62 «Технология продукции и организация общественного питания».
УДК 53
ББК 22.3
Ф 912
© М.А. Фролов, 2012
© Л.А. Ашихина, 2012
© Орел ГИЭТ , 2012
СОДЕРЖАНИЕ
ПРАВИЛА ТехникИ безопасности при выполнении лабораторных работ (ЧастЬ II) 4
Рекомендации к подготовке и выполнению лабораторных работ (частЬ II) 4
Лабораторная работа №4
Изучение законов колебательного движения. 5
Лабораторная работа №5
Определение коэффициента внутреннего трения жидкостей. 13
Лабораторная работа №6
Определение коэффициента поверхностного натяжения жидкости. 20
Лабораторная работа №7
Определение отношения теплоёмкостей газа при постоянном давлении
и постоянном объёме методом адиабатического расширения. 27
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 35
ПРАВИЛА ТехникИ безопасности при выполнении
Лабораторных работ (частЬ II )
При выполнении лабораторных работ части II необходимо знать и строго соблюдать общие правила техники безопасности п.1-9 (часть I). Кроме того, применительно к лабораторным работам 4-7 необходимо дополнительно соблюдать следующие правила техники безопасности.
При выполнении лабораторной работы № 4:
1. физический маятник снимать с кронштейна, вешать на кронштейн и переносить для уравновешивания на рабочее место только в вертикальном положении;
2. при уравновешивании физического маятника винты, фиксирующие грузы маятника не раскручивать, во избежание соскакивания грузов с маятника при переводе его в вертикальное положение.
При выполнении лабораторной работы № 5:
1. во избежание повреждения стеклянного цилиндра с маслом категорически запрещается перемещать техническую ложку для подъёма шариков со дна цилиндра;
2. во избежание свёртывания барабана микрометра и деформации свинцовых шариков при измерении их диаметров, барабан вращать только за трещотку.
При выполнении лабораторной работы № 6:
1. во избежание повреждения тонкого стеклянного капилляра и пробирок, категорически запрещается самостоятельно, без разрешения преподавателя, переставлять стеклянный капилляр из исследуемой пробирки в эталонную и наоборот;
2. заливать воду в аспиратор можно только при закрытом кране аспиратора.
При выполнении лабораторной работы № 7:
1. запрещается использование насоса Камовского при закрытом кране нагнетания (откачки) воздуха в стеклянный баллон;
2. во избежание выплёскивания жидкости из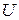 
- образного манометра, насосом Камовского не делать более 3-х качков.
рекомендации к подготовке и выполнению
ЛАБОРАТОРНАЯ РАБОТА№4
Краткая теория
Колебания представляют один из наиболее распространённых видов движений и весьма разнообразны по своей физической природе. Маятник часов, звук, свет, переменный электрический ток являются примерами колебаний тех или иных физических величин. Однако при всём разнообразии колебаний (механических или электромагнитных) закономерности колебательных процессов имеют между собой много общего.
Напомним, что колебательным движением твёрдого тела (системы) называется движение, характеризующееся той или иной степенью повторяемости во времени. Колебания, при которых движение тела повторяется через равные промежутки времени, называются периодическими колебаниями. Для характеристики периодического колебательного движения используются такие величины, как смещение (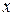 
), амплитуда ( 
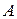), период ( 
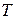) и частота ( 
).
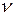Смещением называется величина, характеризующая положение тела в данный момент времени относительно его положения равновесия.
Наибольшее отклонение тела от положения равновесия называется амплитудой колебаний.
Наименьший промежуток времени, по истечении которого движение тела (системы) повторяется, называется периодом колебаний. Величина обратная периоду колебаний, называется частотой колебаний. Она определяет число полных колебаний за единицу времени, т. е.
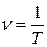. (1)
За единицу частоты в СИ принимается частота такого колебания, период которого равен 1 секунде. Эту единицу называют герцем (Гц).
Важной характеристикой колебательного движения является так называемая круговая (циклическая) частота:
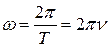, (2)
которая определяет число колебаний тела за 2π секунд.
Простейшим случаем периодического колебательного движения являются гармонические колебания, при которых изучаемая физическая величина изменяется по закону синуса или косинуса.
Гармонические колебания совершает, например, тело, на которое действует только упругая или квазиупругая сила.
Квазиупругой силой называется сила, которая не является по своей природе упругой, но пропорциональна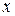 
, то есть она удовлетворяет тому же условию, как и упругая сила
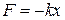, (3)
где 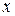— смещение тела от положения равновесия.
Если гармонические колебания происходят только под действием упругой или квазиупругой силы, то частота колебаний не зависит от начальных условий и определяется только свойствами самой колеблющейся системы. На этом основании эта частота называется собственной частотой и обозначается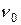 
или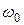 
, а сами колебания называются собственными или свободными колебаниями.
Гармонические колебания тела описываются линейным однородным дифференциальным уравнением второго порядка
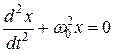. (4)
Решение этого уравнения может быть записано в следующем виде:
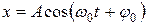, (5)
или
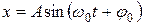, (6)
где 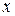— смещение (отклонение) колеблющейся системы от положения равновесия; 
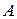— амплитуда колебания.
Аргумент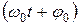 
стоящий под знаком косинуса (синуса), носит название фазы колебания. Величина 
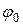называется начальной фазой.
Начальная фаза характеризует колебательный процесс в начальный момент времени, т. е. при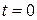 
. Фаза, как физическая величина, сама является функцией времени. В случае гармонических колебаний фаза определяется, как уже отмечалось выше, равенством:
.
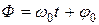Легко убедиться в том, что первая и вторая производные от гармонически колеблющейся величины 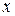также изменяются по гармоническому закону. Так, например, дифференцируя (6) имеем:
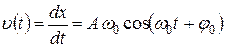, (7)
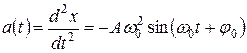. (8)
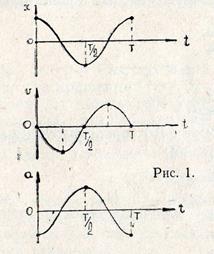
Из (7) и (8) следует, что при гармонических колебаниях скорость и ускорение тела, также как и его смещение, изменяются по периодическому (гармоническому) закону. При этом скорость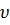 
опережает смещение по фазе на 
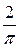, а ускорение ( 
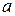) и смещение ( 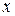) находятся в противофазе. Это хорошо видно на рис. 1, где показаны графики изменения во времени смещения 
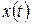, скорости 
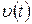и ускорения 
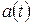для одной и той же механической колебательной системы.
При изучении законов колебательного движения механических систем в лабораторных условиях, как правило, используют колебательные системы, имеющие одну степень свободы. К числу таких систем относятся математический маятник на бифилярном подвесе и физический маятник.
Физическим маятником называется тело, укреплённое на неподвижной горизонтальной оси, не проходящей через его центр масс, и способное совершать колебания относительно этой оси.
При отклонении маятника от положения равновесия на некоторый угол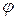 
возникает вращающий момент, стремящийся вернуть маятник в положение равновесия.
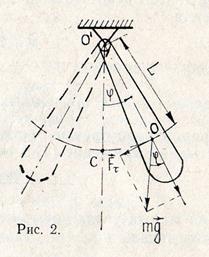
Величина этого момента, как это следует из рис. 2, равна:
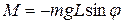(9)
где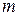 
— масса маятника; 
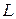— расстояние между точкой подвеса и центром масс маятника. Знак «–» в формуле (9) объясняется тем, что векторы 
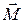и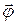 
направлены в противоположные стороны.
В случае малых отклонений от положения равновесия физический маятник совершает гармонические колебания. Докажем это.
Пусть точка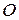 
является центром масс физического маятника. В процессе колебаний центр масс тела совершает движение по дуге окружности радиуса 
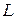. Обозначим момент инерции маятника относительно оси вращения, проходящей через точку 
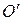, символом 
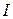. Согласно основному закону динамики вращательного движения
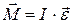, (10)
где
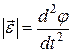. (11)
Приравнивая правые части (9) и (10), пренебрегая трением и учитывая выражение (11), получаем:
.
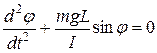При малых углах отклонения маятника можно принять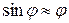 
, тогда:
,
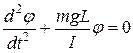а вводя обозначение
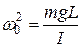, (12)
получим уравнение, аналогичное (4):
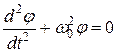. (13)
Решение этого дифференциального уравнения аналогично (5) и записывается в виде:
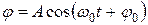. (14)
Из (14) следует, что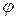 
является периодической функцией и изменяется по закону косинуса. Правильность этого решения можно проверить, дифференцируя (14) два раза по времени.
Следовательно, можно считать, что физический маятник, отклонённый на малый угол, (когда выполняется условие 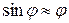), будет совершать гармонические колебания. Период колебания физического маятника определяется выражением:
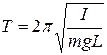, (15)
что следует из формулы (2) с учётом (12).
В (15) символом 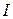обозначен момент инерции физического маятника относительно оси, проходящей через точку 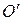рис. 2.
Напомним, что момент инерции твёрдого тела относительно заданной оси равен сумме моментов инерции отдельных составляющих его частиц (материальных точек):
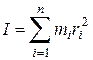, (16)
где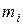 
и 
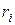— соответственно масса i-й частицы и её расстояние до оси вращения (i = l, 2,…, п).
Если для какого-либо тела известен его момент инерции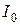 
относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, может быть найден по теореме Штейнера:
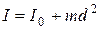, (17)
где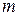 
— масса тела, 
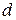— расстояние между осями.
В данной лабораторной работе формулы (15) и (17) используются для определения момента инерции физического маятника (задание № 1).
Математическим маятником называется колебательная система, состоящая из материальной точки, «прикреплённой» к концу гибкой, нерастяжимой и невесомой нити, второй конец которой закреплён неподвижно. Близким к математическому, является маятник, представляющий собой тяжёлый шарик, подвешенный на тонкой нерастяжимой нити (рис. 3).
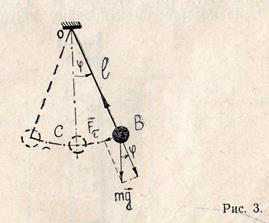Отклонение маятника от положения равновесия будем характеризовать углом 
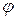, образованным с нитью вертикально.
При отклонении маятника от положения равновесия возникает вращающий момент, модуль которого равен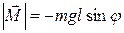 
, где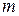 
— масса, а 
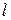— длина маятника.
При малых углах 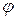(когда можно принять 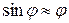) свободные колебания математического маятника можно считать гармоническими с периодом:
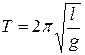(18)
где 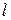— длина маятника, 
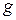— ускорение силы тяжести.
Малые колебания математического маятника (когда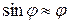 
) являются также гармоническими (аналогично физическому маятнику). Формула (18) получается, если в (15) подставить значение момента инерции математического маятника относительно точки подвеса: 
.
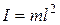Как следует из формулы (18), период колебаний математического маятника зависит (при отсутствии трения) только от его длины 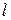и ускорения силы тяжести 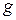. Экспериментальная проверка указанной зависимости и составляет содержание задания № 2 данной лабораторной работы.
Описание установки
В данной лабораторной работе законы колебательного движения будем изучать с помощью универсального маятника (прибор ФП1А).
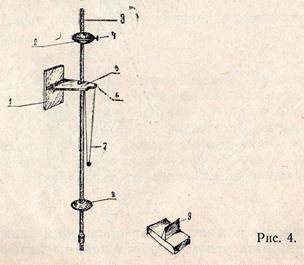
Прибор ФП1А (рис. 4) включает в себя настенный кронштейн 1, на котором смонтирована подушка опорных призм 5 и узел 6 крепления нитей бифилярного подвеса математического маятника 7. На кронштейне 1 подвешен (на опорной призме 5) физический маятник, представляющий собой металлический стержень 3, на котором закреплены два тяжелых груза — чечевицы 2 и 8. Таким образом, универсальный маятник (прибор ФП1А) сочетает в себе два типа маятников: физический и математический. Конструкция прибора обеспечивает вращение обоих маятников около одной и той же оси, проходящей через опорную плоскость подушек 5.
В комплект прибора входит специальная подставка 9 с призмой для нахождения центра масс маятника.
Порядок выполнения работы
Задание 1. Определение момента инерции физического маятника.
Приборы и принадлежности : физический маятник (прибор ФП1А), секундомер, металлическая линейка с ценой деления 1 мм, подставка с призмой для нахождения центра тяжести маятника.
При выполнении задания № 1 рекомендуется соблюдать указанную ниже последовательность выполнения работы.
1. Вывести и записать, используя выражение (15), расчётную формулу для определения момента инерции физического маятника.
2. Приготовить таблицу для записи исходных данных и результатов опыта (табл. 1).
| Номер опыта | m, кг | ∆ m, кг | L, м | ∆ L, м | N | τ, с | Т, с | ∆Т, с | I, кг·м2 | ∆ I, кг·м2 |
| 1 . . . n |
3. Зафиксировать грузы (чечевицы) на стержне физического маятника по указанию преподавателя.
Определить и записать в табл. 1 массу т физического маятника (масса обычно указана на маятнике или сообщается преподавателем).
4. Положить маятник на ребро трёхгранной призмы (рис.5) и, добившись положения устойчивого равновесия маятника, измерить длину L от точки подвеса до центра масс этого маятника. Указанные измерения величины L выполнить не менее 5-ти раз. Результаты всех измерений записать в табл. 1.
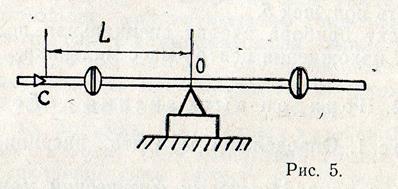5. Повесить маятник на кронштейн 1 (рис. 4). Отклонить маятник на угол 5—10° и предоставить ему возможность совершать малые колебания.
6. Измерить с помощью секундомера время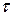 
20-ти полных колебаний. Измерения 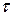повторить не менее 5-ти раз. Число полных колебаний N может быть и другим (N = 30, N=40 и т. д.). Результаты всех измерений записать в табл. 1.
ЛАБОРАТОРНАЯ РАБОТА № 5
Краткая теория
Внутреннее трение (вязкость) жидкостей относится к разделу физики, называемому физической кинетикой, предметом изучения которой являются необратимые процессы. Свойства каждого кинетического процесса определяются как внешними условиями, в которых находится вещество, так и внутренними свойствами вещества. Изучение кинетических процессов является источником ценной информации о силах взаимодействия между частицами вещества.
Каждый кинетический процесс приводит хотя бы к одному из явлений переноса, которые называются диффузией, теплопроводностью, вязкостью, электропроводностью.
Диффузия (перенос вещества), теплопроводность (перенос энергии в форме тепла), вязкость (перенос импульса) являются необратимыми процессами, возникающими самопроизвольно вследствие теплового движения при отклонении вещества от равновесного состояния. Это отклонение выражается соответственно в неоднородном распределении вещества, его температуры, в различии скоростей движения макроскопических частиц среды.
Механизм вязкости заключается в молекулярном перемешивании, обусловленном тепловым движением. Вязкость проявляется в появлении силы сопротивления относительному движению слоёв жидкости или газа. Основным феноменологическим законом, описывающим явление вязкости, является закон Ньютона:
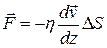, (1)
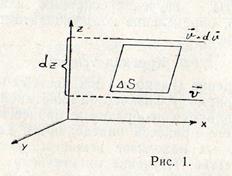где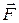 
— сила внутреннего трения соприкасающихся слоёв жидкости (газа); 
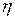— коэффициент внутреннего трения или динамической вязкости; 
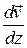- градиент скорости упорядоченного движения, характеризующий изменение скорости потока вдоль оси 
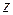(см. рис. 1); 
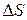— величина площади соприкасающихся слоев; 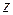— направление, перпендикулярное скорости движения слоёв жидкости (газа).
Единицей вязкости в СИ является такая вязкость, при которой градиент скорости, равный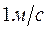 
на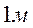 
, приводит к возникновению силы внутреннего трения в 
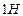на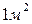 
. Таким образом, коэффициент динамической вязкости имеет размерность
.
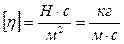Широко применяется и единица измерения вязкости системы СГС, названная пуазом (Пз) в честь французского учёного Ж. Пуазейля, впервые в середине прошлого столетия исследовавшегося течения вязкой жидкости:
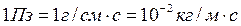. (2)
Свойства течения вязкой жидкости зависят от её плотности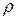 
, динамической вязкости 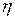, а также от характерных для данного течения скорости 
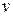и линейного размера 
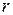. Например, для течения, вызванного движением шара, характерным размером является радиус шара, а характерная скорость — скорость движения шара. Для течения жидкости по трубе характерным линейным размером является диаметр трубы, а характерной скоростью — средняя скорость потока.
Легко показать, что из величин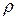 
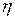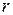, , и 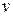можно образовать лишь одну безразмерную комбинацию, названную числом Рейнольдса и обозначаемую через Re:
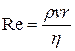. (3)
Число Рейнольдса является одной из важнейших характеристик течения вязкой жидкости, от его значения зависит характер течения, которое может быть ламинарным или турбулентным.
Для каждого течения жидкости существует такое критическое значение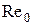 
, что при 
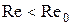возможно только ламинарное течение, а при 
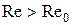течение становится турбулентным. Так, для течения, вызванного движением шара 
.
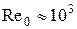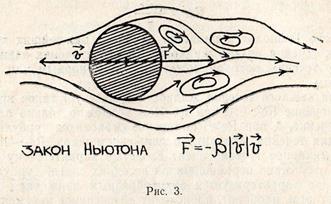
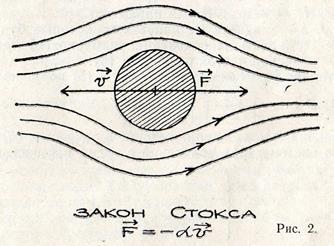Ламинарное течение носит слоистый характер, ему свойственно отсутствие перемешивания соседних слоёв. Турбулентное движение характеризуется вихреобразным движением среды, при котором, наоборот, происходит интенсивное перемешивание вещества в макроскопических масштабах. Эти два режима течения характеризуются различными зависимостями силы сопротивления от скорости (см. рис. 2, 3).
Установим, с какой силой вязкая среда действует на движущееся в ней тело. Рассмотрим вначале ламинарное течение, которое имеет место при малых скоростях течения. Критерием малости является условие:
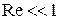. (4)
В этом случае сила сопротивления обусловлена переносом импульса и зависит от динамической вязкости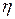 
, скорости течения 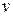и характерного размера 
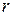. Установим зависимость силы сопротивления от физических параметров методом анализа размерностей. Предполагая, что искомая функциональная зависимость является степенной, можем записать:
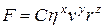, (5)
где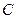 
— безразмерный параметр; 
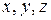— неизвестные константы, которые будут определены из сравнения размерностей правой и левой частей равенства (5).
Подставляя размерность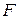 
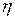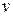, , и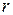 
в (5) получаем:
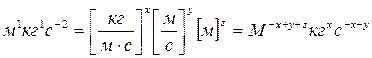. (6)
Приравнивая показатели степеней в равенстве (6), получаем линейную систему трёх уравнений с тремя неизвестными:
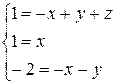
Единственным решением этой системы является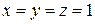 
, что позволяет однозначно установить функциональную зависимость (5):
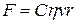, (7)
где безразмерный коэффициент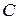 
зависит от формы тела и методом анализа размерностей, естественно, определён быть не может. Английский ученый Дж. Стокс показал, что для шара
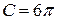и 
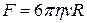, (8)
где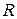 
— радиус шара.
При турбулентном движении (большие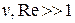 
) перемешивание жидкости становится макроскопическим и определяющей становится не вязкость жидкости, а её плотность 
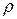. Методом анализа размерностей легко показать, что в этом случае
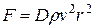, (9)
где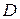 
— безразмерный коэффициент, сильно зависящий от формы тела. В общем случае закон действия силы сопротивления имеет вид:
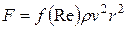, (10)
где безразмерная функция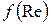 
определяется экспериментально.
Анализ размерностей является одним из универсальных методов исследования физических явлений и очень прост в применении.
(Великий физик Энрико Ферми часто повторял, что действительно понимающие природу того или иного явления должны получать основные соотношения из соображений размерности).
Динамическая вязкость газов растёт с увеличением температуры по закону, близкому к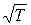 
. Незначительные отклонения от этого закона обусловлены небольшим изменением эффективного сечения молекул 
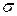с температурой.
Динамическая вязкость жидкостей с увеличением температуры сильно уменьшается в соответствии с законом, открытым советским физиком Я. И. Френкелем (закон Френкеля-Андраде):
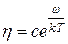, (11)
где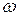 
— энергия активации молекулы; 
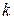— постоянная Больцмана, а множитель 
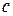зависит от химического состава жидкости и слабо — от температуры. Например, вязкость воды при изменении температуры от 0°С до 100°С уменьшается от 
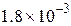до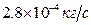 
.
Динамическая вязкость некоторых жидкостей при различных температурах приведена в табл. 1.
Таблица 1
| Жидкость |  ,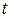
|  ,
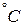
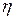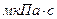
| Жидкость |  ,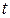
|  ,
|
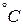
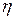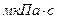
| Вода | 0 | 1788 | Масло касторовое | 10 | 242·104 |
| 20 | 1004 | Масло подсолнечное | 20 100 | 50000 2770 | |
| Глицерин | -20 | 134·106 | |||
| 0 | 121·105 | Мёд | 20 | 650·104 | |
| 20 | 1499·103 | 80 | 100·103 | ||
| 100 | 12945 | ||||
| 200 | 216 | Молоко цельное | 5 20 | 2960 1790 | |
| Молоко сгущенное | 20 | 1245·103 | 80 | 570 | |
| (с сахаром) | |||||
| Рыбий жир | 20 | 45600 | |||
| Раствор спирта этилового в воде (20%-ный) | 20 | 1960 | Сливки (жирностью 40%) | 80 20 | 4600 6900 |
Теория метода Стокса
Одним из способов определения коэффициента вязкости является метод Стокса, основанный на использовании закона Стокса (8) и измерении времени (скорости) движения в исследуемой жидкости тяжёлого металлического шарика малого радиуса.
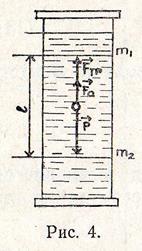
Если небольшой шарик падает вертикально в вязкой жидкости, то он испытывает действие трёх коллинеарных сил (см. рис. 4): силы тяжести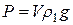 
, выталкивающей силы Архимеда 
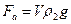и силы сопротивления (трения):
,
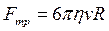где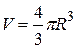 
— объём шарика; 
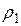и 
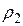– плотности материала шарика и исследуемой жидкости соответственно.
На основании второго закона Ньютона имеем:
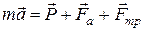, (12)
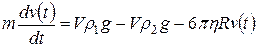. (12΄)
Решением этого уравнения, удовлетворяющим начальному условию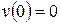 
, является:
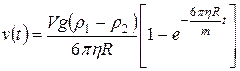. (13)
Через небольшой промежуток времени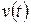 
становится почти постоянной (скорость установившегося движения) и равной
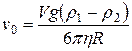. (14)
Решая это уравнение относительно 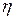и переходя к диаметру шарика 
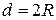, получаем:
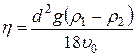. (15)
Скорость установившегося движения вычисляется по экспериментально измеряемому времени 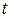его движения (падения) на участие длины 
:
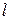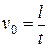. (16)
Окончательно расчётная формула для определения коэффициента вязкости 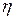примет вид:
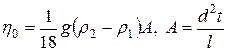, (17)
где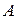 
содержит все экспериментально измеряемые физические величины.
Формулы (15) и (17) справедливы для шарика, движущегося в бесконечно простирающейся жидкости. Для учёта влияния стенок и дна цилиндра, а также верхней поверхности жидкости на движение шарика необходимо в формулу (17) ввести безразмерный поправочный множитель:
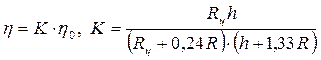(18)
4. Описание установки
Приборы для измерения вязкости жидкости называются вискозиметрами. В данной работе применяется прибор, представляющий собой высокий стеклянный цилиндр, установленный вертикально (рис. 4), в который налита исследуемая жидкость. Сосуд накрыт крышкой с отверстием, через которое при опытах опускаются металлические шарики небольшого диаметра. На цилиндре имеются две метк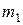и 
и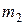 
, расположенные на расстоянии 
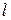друг от друга.
Уровень жидкости в сосуде должен быть выше верхней метки на 8-10 см. Это необходимо для того, чтобы к моменту подхода шарика к верхней метке движение шарика уже было бы установившимся, т. е. выполнялось условие (15). Расстояние между метками можно изменять только за счёт перемещения нижней метки .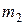
Порядок выполнения работы
1. Ознакомиться с лабораторной установкой и проверить её исправность.
2. Измерить расстояние 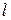между меткам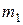и 
и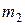 
.
3. Измерить микрометром диаметр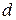 
шарика и опустить этот шарик в сосуд с жидкостью.
4. В момент прохождения шарика мимо метки 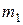включить секундомер. При этом глаз наблюдателя должен находиться на одном уровне с меткой .
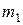5. Остановить секундомер в момент прохождения шарика мимо нижней метки 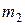. При этом глаз наблюдателя должен находиться на уровне метки .
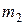6. Произвести отсчёт по секундомеру времени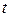 
движения шарика между меткам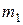и и .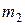
7. Повторить подобный опыт не менее пяти раз, выполняя каждый раз последовательно все пункты 2-6.
8. Температура оказывает заметное влияние на коэффициент вязкости, поэтому следует записать температуру, при которой производят опыт. Плотность шарика и плотность жидкости указаны на установке.
ЛАБОРАТОРНАЯ РАБОТА № 6
НАТЯЖЕНИЯ ЖИДКОСТИ
1. Цель работы: Изучение явления поверхностного натяжения жидкостей, определение коэффициента поверхностного натяжения жидкости методом Ребиндера.
Краткая теория
Молекулы в жидкости расположены настолько близко друг к другу, что между ними возникают значительные силы взаимодействия. Известно, что силы взаимодействия молекул быстро убывают с увеличением расстояния между ними. Следовательно, силы взаимодействия между молекулами жидкости существенно больше, чем силы взаимодействия между молекулами жидкости и молекулами её пара.
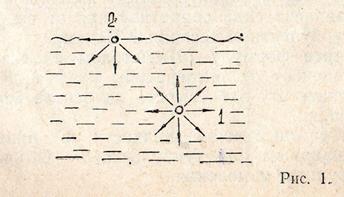Если взять (рис. 1) молекулу 1, находящуюся в глубине жидкости, то она подвержена воздействию соседних молекул со всех сторон в одинаковой мере и поэтому равнодействующая всех молекулярных сил, действующих на неё, равна нулю.
Чем ближе к поверхности молекула, тем больше и равнодействующая, направленная внутрь жидкости. Таким образом, все молекулы, лежащие у поверхности, испытывают силы, стремящиеся втянуть их внутрь жидкости. Для молекулы 2, находящейся на поверхности жидкости, силы молекулярного притяжения направлены только по касательной к поверхности и внутрь жидкости.
Силы, направленные перпендикулярно поверхности и сжимающие нижележащие слои, называются силами молекулярного давления. Силы, направленные по поверхности жидкости и стремящиеся сократить эту поверхность, называются силами поверхностного натяжения. Под влиянием этих сил поверхностный слой жидкости приходит в состояние, напоминающее растянутую упругую плёнку, стремящуюся сократиться. Для того чтобы такую плёнку удержать в равновесии, к линии её границы надо приложить силу F , касательную к поверхности жидкости, называемую силой поверхностного натяжения. Эта сила тем больше, чем больше длина границы пленки l , т. е.
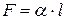(1)
или
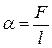, (2)
где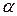 
— коэффициент поверхностного натяжения жидкости.
Таким образом, коэффициент поверхностного натяжения определяется силой поверхностного натяжения, действующей на единицу длины границы поверхности жидкости. В системе СИ коэффициент поверхностного натяжения имеет размерность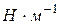 
.
Сила поверхностного натяжения всегда направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует.
Зная силу поверхностного натяжения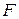 
, можно вычислить работу 
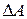, которую надо совершить, чтобы увеличить поверхность жидкости на величину 
.
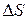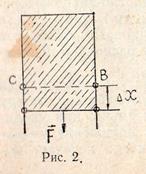
Рассмотрим рис. 2. На нём изображен проволочный прямоугольный каркас, нижняя сторона которого (проволочка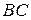 
длиной 
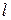) сделана подвижной. Предположим, что этот каркас заполнен мыльной плёнкой, которая представляет собой мыльную воду, имеющую два поверхностных слоя.
Под действием сил поверхностного натяжения свободная поверхность плёнки стремится сократиться. Чтобы удержать плёнку в равновесии, надо, согласно формуле (1), к проволочке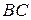 
приложить силу, которая равна
.
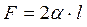Пусть граница поверхности жидкости длиной 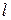передвинулась в направлении действующей силы 
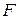на расстояние 
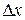. При этом будет совершена работа:
.
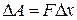С учётом выражения для силы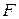 
имеем:
,
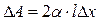или
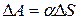, (3)
откуда
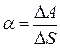, (4)
где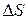 
– приращение площади свободной поверхности жидкости. Из (4) следует, что коэффициент поверхностного натяжения 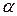определяется работой, которую необходимо затратить для увеличения поверхности жидкости на единицу площади. Таким образом, в системе СИ коэффициент поверхностного натяжения можно измерять не только в ньютонах на метр ( 
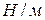), но и в джоулях на квадратный метр ( 
).
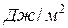Наибольшие значения коэффициента поверхностного натяжения имеют жидкости с наиболее прочными связями между их молекулами. Так, например, для ртути относительно её пара коэффициент поверхностного натяжения (при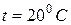 
) равен 
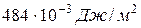, а для анилина в тех же условиях — 
.
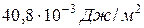Коэффициент поверхностного натяжения различен для различных жидкостей, а для одной и той же жидкости он существенно зависит от температуры жидкости (табл. 1) и наличия в ней примесей, особенно примесей поверхностно-активных веществ (жирные кислоты, их соли, спирты и др.), так как для переноса молекул этих веществ к поверхности требуется меньше энергии, чем для переноса молекул исследуемой жидкости.
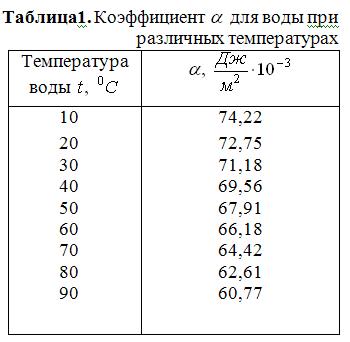Зависимость коэффициента 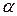от температуры объясняется тем, что при повышении температуры взаимодействие между молекулами жидкости ослабляется. Следовательно, при увеличении температуры жидкости поверхностное натяжение уменьшается. Вблизи критической температуры, когда исчезает поверхность раздела жидкость-пар, коэффициент поверхностного натяжения данной жидкости обращается в нуль.
Существует несколько методов определения коэффициента поверхностного натяжения. В основе этих методов лежат следующие закономерности.
Если поверхностный слой жидкости не плоский, а имеет кривизну, то силы поверхностного натяжения создают в таком слое избыточное давление, обусловленное кривизной поверхностного слоя. Это избыточное давление определяется формулой Лапласа:
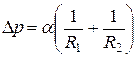, (5)
где 
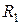и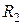 
— главные радиусы кривизны поверхности в рассматриваемой точке.
Добавочное давление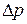 
направлено всегда к центру кривизны поверхности (в случае выпуклой поверхности жидкости дополнительное давление направлено внутрь жидкости, в случае вогнутой — наружу). Поверхность жидкости в узких трубках ( капиллярах ) называют мениском. Для смачивающей жидкости (когда силы взаимодействия между молекулами жидкости слабее взаимодействия между молекулами жидкости и твёрдого тела) мениск вогнутый. Если жидкость не смачивает твёрдое тело (сила сцепления между молекулами жидкости твёрдого тела меньше сил взаимодействия между молекулами жидкости), мениск выпуклый. В узких капиллярах поверхность мениска можно считать частью сферы, то есть можно принимать 
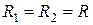. Тогда формула (5) будет иметь вид:
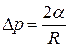. (6)
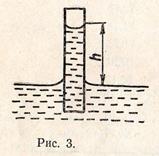Под действием отрицательного избыточного давления смачивающая жидкость поднимется по капилляру на некоторую высоту h (рис. 3), при которой избыточное Лапласово давление будет уравновешено гидрастатическим давлением поднявшегося столбика жидкости:
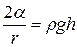, (7)
где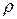 
— плотность жидкости; 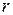— радиус капилляра;
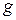— ускорение силы тяжести.
Из соотношения (7) получают формулу для определения коэффициента поверхностного натяжения:
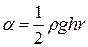. (8)
Заметим, что формула (8) справедлива только при условии полного смачивания стенок капилляра исследуемой жидкостью.
Если в верхней части капилляра, опущенного нижним концом в жидкость (рис. 3), создавать давление больше атмосферного, то поверхность жидкости внутри капилляра под воздействием этого давления начнет опускаться до тех пор, пока у нижнего конца капилляра не образуется воздушный пузырёк того же диаметра, что и диаметр капилляра. Затем, при дальнейшем увеличении давления, пузырёк отрывается от капилляра. Измеряя давление, соответствующее моменту отрыва пузырька, можно определить величину коэффициента поверхностного натяжения исследуемой жидкости. Метод определения коэффициента поверхностного натяжения жидкости путём измерения наибольшего давления пузырьков предложен академиком П. А. Ребиндером.
Существуют и другие методы определения коэффициента 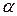, например, с помощью весов Жолли. В данной работе используется метод Ребиндера.
Описание установки
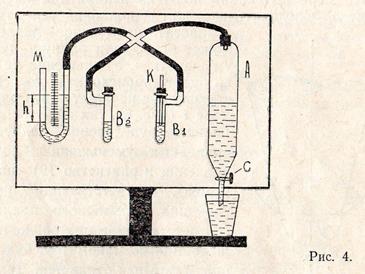Основными элементами установки для определения коэффициента поверхностного натяжения жидкости методом академика П. А. Ребиндера являются: жидкостный манометр 
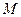, аспиратор 
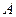, две пробирк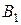и 
и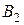 
, тонкая стеклянная трубка 
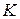с концом, оттянутым в капилляр. Схема соединения перечисленных элементов показана на рис. 4.
Перед началом опыта аспиратор 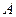(при закрытом кране) наполняется водой, в пробирку 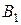наливается исследуемая жидкость (например, спирт), в пробирку 
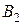— эталонная жидкость (например, дистиллированная вода). В одну из пробирок, например 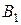, через отверстие в пробке вставляется трубочка 
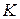так, чтобы её оттянутый под капилляр кончик едва касался бы поверхности жидкости.
Если слегка приоткрыть кран аспиратора, то вода начнёт медленно вытекать из него, и в верхней части аспиратора, а следовательно и в верхней части пробирок 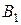и 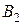, а также в правом колене манометра образуется разряжение. Давление 
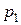над уровнями жидкости в аспираторе и пробирках будет меньше атмосферного 
:
.
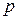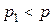В процессе дальнейшего разряжения воздуха в пробирке 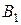поверхность жидкости на «кончике» капилляра начинает искривляться и становится частью некоторой сферы радиуса 
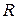(рис. 5). Начинает образовываться воздушный пузырёк. На него со стороны жидкости будет действовать дополнительное давление, определяемое формулой (6). Атмосферное давление 
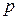будет уравновешиваться давлением воздуха 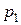, находящимся в аспираторе 
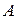и в пробирке 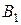и добавочным (Лапласовым) давлением 
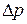. Гидростатическим давлением можно пренебречь. С учётом (6) можно записать:
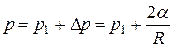. (9)
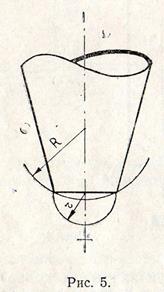По мере вытекания воды из аспиратора уменьшается давление 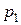. Следовательно, для выполнения условия (9), должно возрастать избыточное давление 
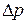. А это может быть, если радиус пузырька будет уменьшаться. Уменьшение радиуса пузырька будет происходить до тех пор, пока этот радиус не будет равен радиусу капилляра 
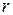(рис. 5), так как любое, даже небольшое увеличение радиуса пузырька приведёт к уменьшению дополнительного давления и равенство (9) нарушается. В момент, соответствующий равенству 
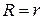, величина избыточного давления, а также соответствующая ему разность 
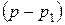, наблюдаемая по манометру, будет максимальной, и пузырек оторвётся. Далее начинается аналогичный процесс формирования нового пузырька.
Для момента отрыва пузырька от капилляра справедливо равенство:
.
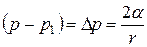Следовательно, измерив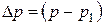 
по манометру 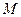и определив радиус 
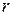капилляра, можно вычислить 
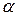. Однако с нужной точностью радиус капилляра определить трудно, поэтому обычно его из расчётной формулы исключают. Для этого вначале проводят опыт с жидкостью, коэффициент поверхностного натяжения 
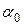которой известен, а затем повторяют опыт с исследуемой жидкостью для определения 
.
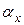Если через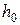 
обозначить величину максимального давления (разность высот в манометре) для эталонной жидкости, а через 
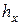- для исследуемой жидкости, то для них соответственно можно написать в момент отрыва пузырька следующие равенства:
, 
.
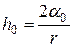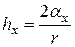Разделив одно равенство на другое, получим
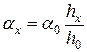. (10)
Из равенства (10) видно, что коэффициент поверхностного натяжения любой жидкости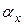 
можно определить, если известен коэффициент поверхностного натяжения другой жидкости 
.
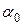В нашем опыте в качестве эталонной жидкости берётся дистиллированная вода при комнатной температуре (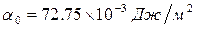 
).
Порядок выполнения работы
1. Ознакомиться с лабораторной установкой и подготовить её для проведения опыта при заданной (комнатной) температуре;
а) налить воду в аспиратор;
б) наполнить дистиллированной водой пробирку ;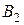
в) наполнить исследуемой жидкостью пробирку ;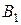
г) опустить капилляр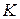 
в сосуд 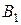настолько, чтобы его конец касался поверхности жидкости.
2. Составить таблицу результатов наблюдений по прилагаемой форме (табл. 2).
Таблица 2.
| Номер опыта | Исследуемая жидкость | Эталонная жидкость |
|
|
| ||||
| Положение уровней в манометре, мм | Положение уровней в манометре, мм | ||||||||
| левый | правый |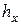 
| левый | правый |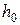
| ||||
1
2
3
…
| |||||||||
,
,
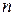
3. Медленно открывая кран аспиратора, добиться появления пузырьков на конце капилляра не группами, а по одному. Это условие необходимо для того, чтобы уровни жидкости в манометре изменялись медленно.
4. Измерить в момент выхода пузырька максимальную разность уровней жидкости 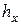в коленах манометра 
.
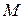5. Повторить измерения 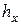не менее 7-10 раз. Результаты занести в табл. 2.
6. Переставить капилляр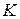 
в трубку 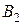и проделать столько же раз аналогичные опыты (выполнить пункты 3, 4, 5) с эталонной жидкостью (водой). Результаты измерений 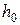занести в таблицу 2.
Примечание: при перестановке капилляра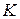 
из трубки 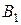в трубку 
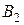его необходимо тщательно просушить.
7. Измерить и записать в свой отчёт температуру, при которой проводились опыты.
ЛАБОРАТОРНАЯ РАБОТА №7
Краткая теория.
Основные закономерности адиабатического процесса изучаются на примере поведения идеального газа.
Идеальный газ — это некий абстрактный газ, удовлетворяющий следующим условиям: 1) соударения молекул такого газа происходят как соударения упругих шаров; 2) размеры молекул пренебрежимо малы; 3) между молекулами отсутствуют силы взаимного притяжения и отталкивания.
Всякий реальный газ по мере убывания его плотности приближается по свойствам к идеальному. Обычный воздух при комнатной температуре и атмосферном давлении можно приближённо считать идеальным газом. Состояние некоторой массы газа определяется значениями трёх параметров: давления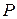 
, объема 
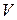и температуры 
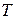. В том случае, когда из этих трёх параметров при изменении состояния газа один остаётся постоянным, процесс перехода называется изопроцессом.
Для идеального газа строго выполняются законы Бойля-Мариотта,
Гей-Люссака и Шарля. Эти законы описывают состояния газа для случаев, когда один из параметров остаётся постоянным.
Закон Бойля-Мариотта описывает изотермический процесс, т. е. процесс, протекающий при постоянной температуре (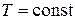 
): для данной массы газа при постоянной температуре произведение давления газа на объём есть величина постоянная
.
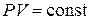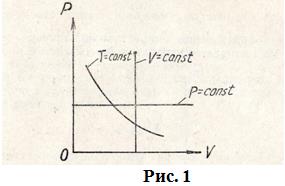
Графически это соотношение изображается гиперболой (рис. 1). Каждому значению температуры соответствует своя кривая. Эти кривые называются изотермами.
Закон Гей-Люссака описывает изобарический процесс, т. е. процесс, протекающий при постоянном давлении (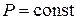 
): отношение объёма данной массы газа к температуре, при которой он находится, есть величина постоянная:
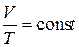. (2)
Закон Шарля описывает изохорический процесс, т. е. процесс, протекающий при постоянном объёме (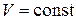 
): отношение давления газа к температуре, при которой он находится, есть величина постоянная:
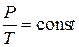. (3)
Графически соотношения (2) и (3) изображены в координатах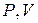 
на рис. 1.
Первое начало термодинамики выражает закон сохранения энергии и формулируется следующим образом: количество тепла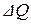 
сообщённое системе, идёт на приращение внутренней энергии 
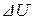системы и на совершение системой работы 
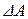против внешних сил:
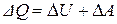. (4)
Для бесконечно малого изменения состояния системы уравнение (4) примет вид:
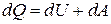. (5)
Адиабатическим процессом называется процесс, протекающий без теплообмена с внешней средой. Близкими к адиабатическому могут быть быстро протекающие процессы, так как количество тепла, которым обменивается система с внешней средой, будет тем меньше, чем меньшее время длится процесс.
Для адиабатического процесса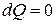 
, тогда из (5) следует:
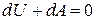
или
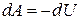, (6)
т. е. работа в адиабатическом процессе совершается за счёт убыли внутренней энергии.
Для идеального газа при адиабатическом процессе функциональная связь между давлением и объёмом определяется уравнением Пуассона:
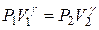, (7)
где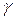 
— показатель степени, численно равный отношению молярных теплоёмкостей данного газа, т. е.:
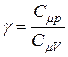. (8)
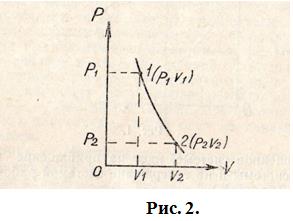
Кривая, изображающая адиабатический процесс в координатах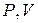 
называется адиабатой (рис. 2).
Теплоёмкость газа — это физическая величина, численно равная количеству тепла, которое необходимо сообщить системе для нагревания её на один Кельвин (градус):
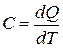. (9)
В системе СИ теплоёмкость имеет размерность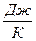 
.
Различают удельную и молярную теплоёмкости.
Теплоёмкость единицы массы вещества называют удельной теплоёмкостью:
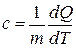. (10)
Она обозначается буквой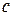 
и имеет и имеет размерность 
.
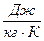Теплоёмкость одного моля вещества называется молярной:
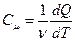, (11)
где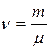 
— число молей вещества; 
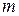— масса вещества; 
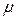— молярная масса. Молярная теплоёмкость имеет размерность 
.
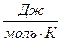Теплоёмкость моля вещества и удельная теплоёмкость связаны очевидным соотношением:
.
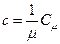Величина теплоёмкости газов существенно зависит от условий, при которых протекает процесс: при постоянном объёме или при постоянном давлении.
Если нагревание газа происходит при постоянном объёме, то газ не совершает работы против внешних сил, так как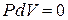 
. Из уравнения первого начала термодинамики следует:
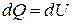, (12)
т. е. при изохорическом процессе всё тепло, сообщенное газу, идёт на приращение его внутренней энергии. Напомним, что внутренняя энергия идеального газа является функцией только температуры. Следовательно, для одного моля идеального газа имеем:
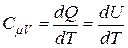. (13)
Внутренняя энергия одного моля идеального газа определяется уравнением:
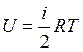, (14)
где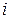 
— число степеней свободы молекулы данного газа (число независимых координат, которые полностью определяют положение молекулы в пространстве, называется числом степеней свободы молекулы); 
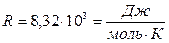- универсальная газовая постоянная.
Для бесконечно малого изменения температуры из уравнения (14) следует:
,
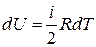откуда
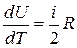. (15)
С учётом (15) выражение (13) приводится к виду
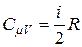. (16)
Если нагревание газа происходит при постоянном давлении, то согласно первому началу термодинамики тепло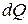 
, сообщённое газу, затрачивается не только на увеличение его внутренней энергии 
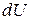, но и на совершение газом работы 
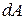, то есть:
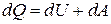. (17)
Для изобарического процесса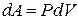 
, поэтому (17) можно записать в виде:
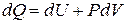
Теплоёмкость моля газа при постоянном давлении равна:
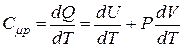. (18)
Первое слагаемое правой части этого равенства равно молярной теплоёмкости газа при постоянном объёме. Запишем уравнение состояния идеального газа для случая бесконечно малого изменения его параметров:
,
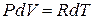откуда
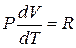. (19)
Таким образом, второе слагаемое равенства (18) численно равно универсальной газовой постоянной .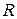
Выражение молярной теплоёмкости газа при постоянном давлении с учётом (15) и (19) приводится к виду:
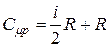, (20)
а так как
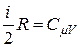, (21)
то
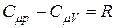. (22)
Это выражение называется уравнением
Майера.
Анализ формул (16) и (20) приводит к выводу, что для идеального газа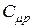 
и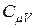 
не зависят от параметров состояния газа 
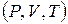, а определяются только числом степеней свободы молекул. Для реальных газов этот вывод удовлетворительно согласуется с опытом при невысоких температурах. При более высоких температурах становится существенной зависимость теплоёмкости и, следовательно, показателя адиабатического процесса 
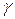от температуры, что необходимо учитывать при расчётах.
Разделив почленно (20) на (16), имеем:
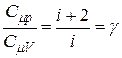. (23)
Так как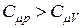 
, то показатель адиабаты 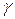всегда больше единицы.
Поэтому адиабата круче спадает к оси абсцисс, чем изотерма (рис. 3).
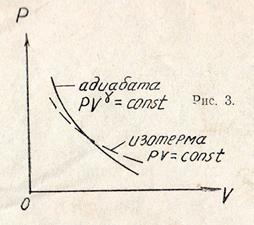Соотношение (23) позволяет вычислить величину 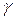для любого газа, если известно число степеней свободы молекул этого газа. Например, для одноатомных газов 
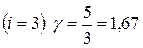; для двухатомных газов 
.
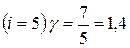Этот результат можно проверить на опыте, что и является целью настоящей работы.
Порядок выполнения работы
1. Составить таблицу для записи результатов.
2. Открыв кран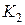 
, накачивают воздух в баллон до тех пор, пока разность уровней жидкости в манометре не будет равна 25-30 см (3-4 качка насосом Камовского). При накачивании воздуха надо следить за тем, чтобы понижающийся в манометре уровень жидкости не доходил до изогнутого нижнего края манометрической трубки.
3. Закрывают кран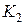 
и ждут 2-3 мин., пока температура внутри баллона не станет равной температуре окружающей среды (давление в сосуде перестанет изменяться). После этого отсчитывают разность уровней жидкости в трубке манометра 
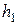. Отсчёт следует делать по нижнему краю мениска.
4. Быстрым нажатием открывают клапан 
, тем самым соединяя баллон с атмосферой. Выдерживают клапан открытым до тех пор, пока уровни жидкости в манометре не сравняются. При этом температура в баллоне понизится. Подождав 2-3 мин., пока температура в баллоне снова не станет равной температуре окружающей среды, отсчитывают показания манометра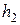 
.
5. Опыт повторить не менее 5 раз, результаты записать в таблицу.
| Номер опыта |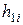 
| 
| 
| 
| 
| 
|
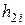
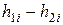
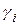
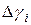
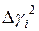
| 1 | ||||||
| … | ||||||
|
6. Рассчитывают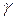 
по формуле (27).
Обработка результатов
1. Вычислить доверительный интервал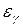 
по заданной доверительной вероятности 
.
.
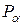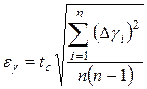2. Оценить границу абсолютной допустимой ошибки линейки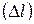 
.
3. Вычислить относительную приборную ошибку, допущенную при определении .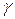
,
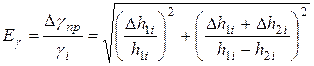где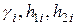 
берутся из таблицы и соответствуют случаю, когда
.
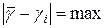4. Вычислить абсолютную приборную погрешность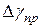 
:
.
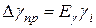5. Сравните абсолютную приборную погрешность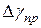 
и доверительный интервал 
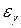. Если они одного порядка, то ошибка измерения 
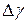вычисляется по формуле:
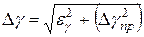
Если они отличаются хотя бы на порядок, то берётся наибольшая ошибка.
6. Окончательный результат запишите в виде:
.
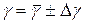Контрольные вопросы
1. Сформулируйте первое начало термодинамики, запишите его и объясните физический смысл всех членов уравнения.
2. Какие процессы называются изохорическими, изобарическими, изотермическими и адиабатическими?
3. Запишите первый закон термодинамики для каждого из этих процессов.
4. Что называется молярной теплоёмкостью? От чего она зависит для идеального газа?
5. Запишите уравнения Пуассона. Что называется коэффициентом Пуассона? Каково его значение для идеального одно- и многоатомного газа?
6. Какая существует связь между внутренней энергией идеального газа и его температурой?
7. Какие процессы происходят с газом в баллоне при выполнении лабораторной работы? Назовите каждый процесс и закон, его описывающий, и напишите математическое выражение этих законов.
8. Постройте графики изопроцессов происходящих в баллоне с газом при выполнении данной лабораторной работы. Приведите примеры изопроцессов из области технологии общественного питания (товароведения и торговой техники).
Рекомендуемая литература
1. Геворкян Р.Г., Шепель В.В. Курс физики. 1959
2. Зисман Г.А., Тодес О.М. Курс общей физики, т. 1. – М.: Наука, 1974. 337 с.
3. Рымкевич А.П. Сборник задач по физике. – М.: Просвещение, 1994. 224 с.
4. Савельев И.В. Курс общей физики, т 1. – М. : Наука, 1987.
5. Трофимова Г.И. Курс физики. Учебник для ВУЗов. М. : Высшая школа, 1989.
6. Шубин А.С. Курс общей физики. – М.: Высшая школа, 1976. – 480 с.
Фролов Марат Александрович
Ашихина Людмила Анатольевна
Лабораторный практикум
по дисциплине «Физика» для студентов
курса всех форм обучения по направлениям
подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
(Часть II )
ОРЕЛ
Издательство ОрелГИЭТ
2012
УДК 53
ББК 22.3
Ф 912
Подготовлено на кафедре математики и естествознания
Рекомендовано Методическим советом инженерно-технологического
факультета
Рецензент: кандидат технических наук, доцент Орловского государственного института экономики и торговли Глазова Г.В.
Фролов М.А., Ашихина Л.А. Лабораторный практикум по дисциплине «Физика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавров: 100800.62 «Товароведение», 260800.62 «Технология продукции и
организация общественного питания» (Часть II). – Орёл: Издательство ОрелГИЭТ, 2012. - 36 с.,
Пособие содержит учебный материал по второй части цикла лабораторных работ по механике, молекулярной физике и термодинамике. Приведены сведения по технике безопасности при выполнении лабораторных работ, контрольные вопросы для самопроверки по каждой лабораторной работе.
Материал данного пособия рекомендуется к использованию при изучении дисциплины «Физика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавриата.100800.62 «Товароведение» и 260800.62 «Технология продукции и организация общественного питания».
УДК 53
ББК 22.3
Ф 912
© М.А. Фролов, 2012
© Л.А. Ашихина, 2012
© Орел ГИЭТ , 2012
СОДЕРЖАНИЕ
ПРАВИЛА ТехникИ безопасности при выполнении лабораторных работ (ЧастЬ II) 4
Рекомендации к подготовке и выполнению лабораторных работ (частЬ II) 4
Лабораторная работа №4
Изучение законов колебательного движения. 5
Лабораторная работа №5
Определение коэффициента внутреннего трения жидкостей. 13
Лабораторная работа №6
Определение коэффициента поверхностного натяжения жидкости. 20
Лабораторная работа №7
Определение отношения теплоёмкостей газа при постоянном давлении
и постоянном объёме методом адиабатического расширения. 27
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 35
Дата: 2018-12-21, просмотров: 408.
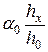
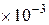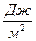
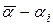
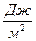
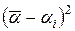
