Для полуограниченной струны

Пусть бесконечная струна в состоянии покоя располагается на участке . Назовем такую струну полуограниченной. Пусть ее левый конец закреплен, так что U(0, t) = 0. В следующей теореме говорится, какую форму U(x, t) имеет такая струна в произвольный момент времени t> 0, когда дополнительно известны начальная форма струны и начальные скорости ее поперечных сечений.

Теорема

Уравнение

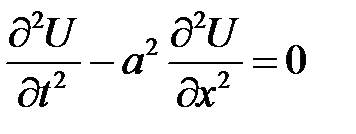
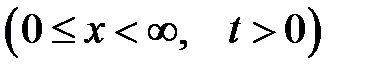
с начальными условиями 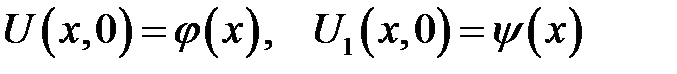 и граничным условием:

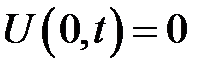                                            (18.1)

имеет следующее решение:

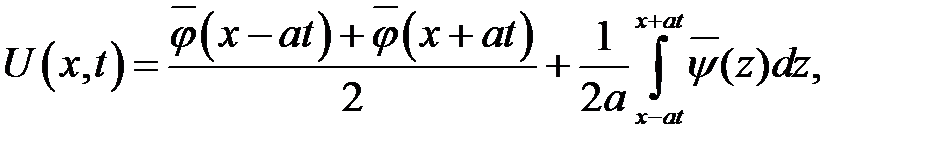
где функции и 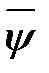являются нечетными продолжениями функци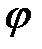й и .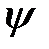

Доказательство.

Функции 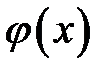, , 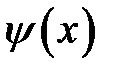заданные в области 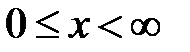, продолжим в область 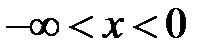нечетным образом. Тем самым мы получим две не-четные функции и :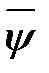

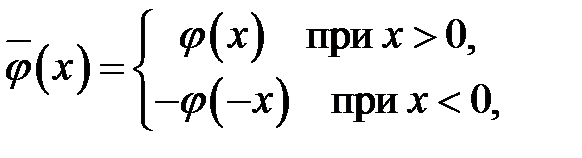
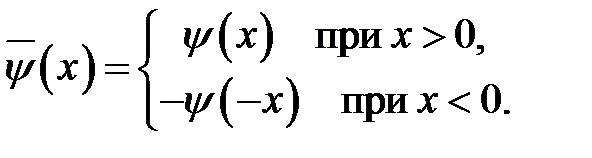
Теперь мы имеем неограниченную струну с известной формой 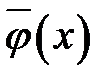и начальными скоростями 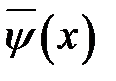сечений. В этом случае, как утверждает предыдущая теорема, решение дается формулой Далам-бера (15.2), из которой вытекает формула (18.2). Убедимся, что ре-шение (18.2) удовлетворяет условию (18.1), подставив в (18.2) зна-чение х = 0

так как и 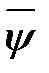— нечетные функции: , .

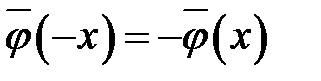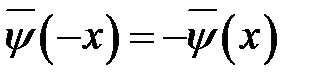Теорема доказана.

Рассмотрим геометрический способ построения решения в двух случаях: когда 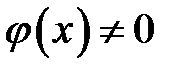,  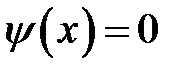(волна отклонения) и когда 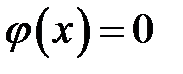,  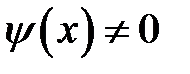(волна импульса). Рассмотрим сначала волну отклонения. Пусть начальный график  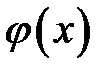полуограниченной струныотличен от нуля на некотором интервале (х₁, х₂), где х₁> 0. Продолжим его в левую сторону 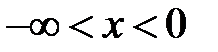нечетным образом. Получится график  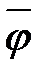неограниченной струны (рис. 18.1, а). Если струну, которую мы отклонили от оси Ох на участке (х₁, х₂), отпустить, то начальное отклонение и его левый двойник раздвоятся на волны вдвое меньшей высоты, бегущие в противоположные стороны (рис. 18.1, б).

Как только волна, бегущая влево, дойдет до начала координат, туда же подойдет ее левый двойник, бегущий вправо (рис. 18.1, б). Затем эти волны начнут накладываться друг на друга (рис. 18.1, в, г, д), что соответствует процессу отражения. Сначала отражающаяся волна укорачивается (рис. 18.1, в), потом исчезает (рис. 18.1, г; если

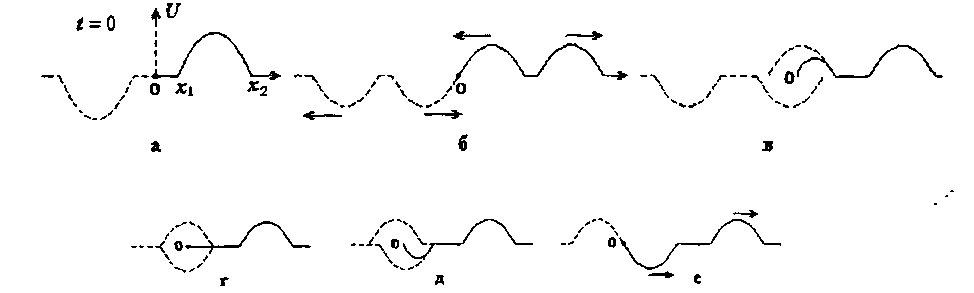
Рис. 18.1

начальное отклонение не было симметрично, то полного исчезно-вения может и не быть), и, наконец, переворачивается (рис. 18.1, д; в этом случае говорят, что фаза волны изменила знак). После этого по струне побегут вправо с одинаковой скоростью две волны, находящиеся в противоположных фазах.

Процесс распространения волны отклонения выглядит следую-щим образом на фазовой плоскости (рис. 18.2).

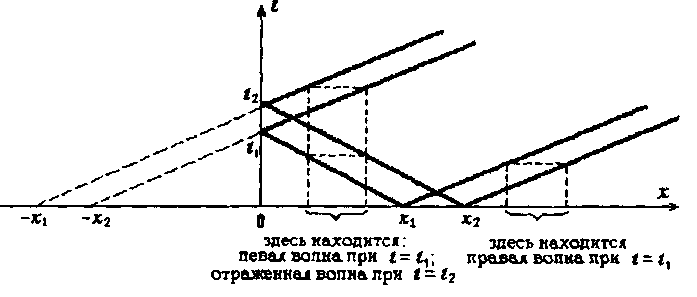
Рис. 18.2

Рассмотрим волну импульса. Снова будем считать, что только сечения струны на участке (х₁, х₂) получили одну и ту же начальную скорость 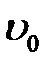. В начальный период времени 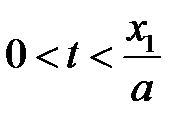, когда волна начинает распространяться и ее левый фронт еще не достиг начала координат, в котором задано граничное условие (18.1), граничное условие не сказывается на процесс распространения волны. Поэтому начало распространения волны происходит так, как это происходит на неограниченной струне (рис. 18.3, а). После того, как волна и бегущий навстречу ее левый двойник встретятся в точке О, они начнут накладываться. Волна будет деформироваться, что соответствует процессу ее отражения в неподвижной точке О (рис. 18.3, б, в, г). После отражения по струне побежит вправо с постоянной скоростью волна в форме трапеции (рис. 18.3, д).

Рис. 18.3