Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

И. В. Добрынина, Р. Р. Яфаева

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО

ЭКОНОМИКО-МАТЕМАТИЧЕСКИМ МОДЕЛЯМ

В УПРАВЛЕНИИ

Тула, 2007

СОДЕРЖАНИЕ

Введение. 3

Лабораторная работа № 1. Задачи линейного и целочисленного линейного программирования. 5

Технология компьютерной реализации. 5

Задача линейного программирования. 5

Пример задачи линейного программирования. 6

Задача целочисленного линейного программирования. 9

Пример задачи целочисленного линейного программирования. 10

Задачи для самостоятельного решения. 13

Лабораторная работа № 2. Задачи транспортного типа. 13

Примеры задач транспортного типа. 14

Задачи для самостоятельного решения. 22

Лабораторная работа № 3. Модели нелинейной оптимизации. 23

Технология компьютерной реализации. 23

Пример задачи нелинейной оптимизации. 24

Задачи для самостоятельного решения. 26

Лабораторная работа № 4. Метод кусочно-линейной аппроксимации. 26

Пример задачи, решаемой методом кусочно-линейной аппроксимации. 27

Задачи для самостоятельного решения. 29

Лабораторная работа № 5. Игровые модели. 29

Пример задачи по теории игр, решаемой симплексным методом.. 30

Задачи для самостоятельного решения. 31

Лабораторная работа № 6. Динамическое программирование. 32

ЛИТЕРАТУРА.. 377

Введение

Методическое пособие предназначено для проведения лабораторных работ по дисциплине «Экономико-математические модели в управлении». При знакомстве с учебным материалом по дисциплине рекомендуется проведение лабораторных занятий.

Цель этих занятий – приобретение навыков компьютерной реализации оптимизационных моделей.

Широкий круг специалистов в своей повседневной практике использует средства Microsoft Office, в частности необходимый компонент расчетов – Microsoft Ехсеl. Пакет Ехсеl содержит специальное средство – команду Сервис/Поиск решения, позволяющую реализовывать модели линейной, нелинейной и дискретной оптимизации.

Для приобретения необходимых практических навыков студентам предлагается ряд типовых экономико-математических задач (об оптимальном использовании ограниченных ресурсов, об инвестициях, о смесях, о раскрое промышленных материалов и др.).

При этом в примере каждого раздела приводится подробное описание технологии получения оптимального решения средствами Ехсеl.

При решении приведенных типовых задач сознательно использовались разнообразные подходы к оформлению рабочей таблицы Ехсеl и результатов решения. В каждой конкретной ситуации студенты могут выбрать свой подход – с позиций содержательности, наглядности, удобства, дизайна.

После отработки типовых задач следует перейти к лабораторной работе.

При этом задачу необходимо правильно понять, записать ее экономико-математическую модель, получить решение на компьютере и дать интерпретацию полученных результатов.

Для успешного выполнения лабораторных работ студент должен знать теоретические основы симплексного метода решения задач, методы ветвей и границ, метода потенциалов, метода кусочно-линейной аппроксимации и иметь представление о матричных антагонистических играх двух участников.

По окончания курса студент должен будет уметь:

– составлять математические модели задач управления;

– находить оптимальные решения задач управления средствами MS Excel;

– анализировать и интерпретировать полученные результаты решения задач.

Компьютерный практикум

Для проведения компьютерного практикума необходима надстройка Поиск решения, которая позволяет реализовывать модели линейной, нелинейной и дискретной оптимизации.

Если в меню Сервис отсутствует команда Поиск решения необходимо выполнить следующие действия:

– выбрать команду Сервис ® Надстройки;

– в диалоговом окне Надстройки установить флажок Поиск решения;

– щелкнуть ОК.

После этого в меню Сервис появится новая команда Поиск решения.

Сокращения

ЭММ		– экономико-математическая модель
ЛП		– линейное программирование
ЗЛП		– задача линейного программирования
ЗЦЛП		– задача целочисленного линейного программирования
ЭТ		–   электронные таблицы
НЛП		– нелинейного программирования
ВП		– выпуклое программирование
ЦФ		–   целевая функция
	–  копировать –  вставить –   мастер функций –  автосумма

Пример задачи линейного программирования

Задача линейного программирования в том или ином виде интерпретируется как задача об оптимальном использовании ограниченных производственных ресурсов.

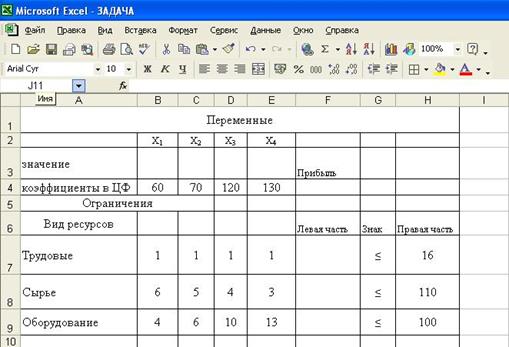
Задача . Предприятие выпускает продукцию четырех видов П₁, П₂, П₃, П₄ с использованием для этого ресурсов, виды и нормы расхода по которым, а также уровень получаемой от их реализации прибыли приведены в таблице. Составьте оптимальный план производства продукции, дающий максимальную прибыль.

Вид ресурса	Вид продукции				Запас ресурса
	П1	П2	П3	П4
Трудовые	1	1	1	1	16
Сырье	6	5	4	3	110
Оборудование	4	6	10	13	100
Прибыль	60	70	120	130

Экономико-математическая модель:

Введём необходимые обозначения: пусть x_j (j=1,2,3,4) – объемы каждого вида продукции. Тогда ЭММ задачи запишется следующим образом:

max f(x₁, x₂, x₃, x₄) =60x₁+70x₂+120x₃+130x₄,

Решение.

1. Создадим форму для ввода условий задачи. Для этого запустим Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. Создадим тексто­вую форму – таблицу для ввода условий задачи.

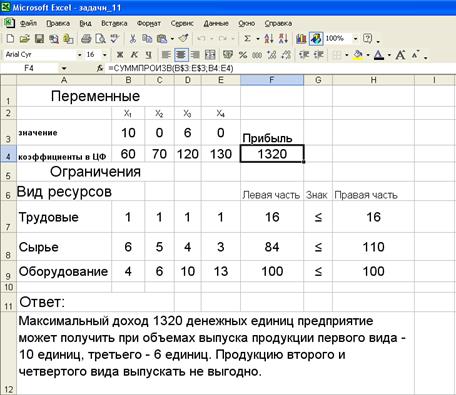
2. Укажем адреса ячеек, в которые будет помещен резуль­тат решения (изменяемые ячейки). Значения компонент вектора X=(x₁, x₂, x₃, x₄) поместим в ячейках ВЗ:ЕЗ, оптимальное значение целевой функции – в ячейку F4.

3. Введем исходные данные задачи в созданную форму-таблицу:

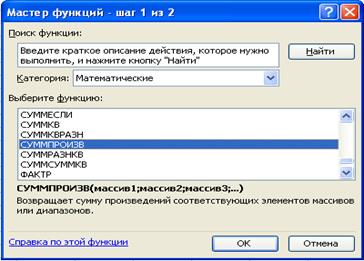
4.Введем зависимость для целевой функции:

· установить курсор в ячейку F4.

· кликнуть по кнопке Мастер функций, расположенной на панели инструментов.

· на экране появляется диалоговое окно Мастер функций – шаг 1 из 2.

· выбрать категорию Математические;

· выбрать функцию СУММПРОИЗВ

· на экране появляется диалоговое окно СУММПРОИЗВ;

· в строку Массив 1 введем В$3:Е$3;

· в строку Массив 2 введем В4:Е4;

· кликнуть по кнопке ОК. На экране в ячейку F4 введена функция.

 

5. Ввести зависимости для ограничений:

· курсор в ячейку F4; кнопка Копировать;

· курсор в ячейку F7; кнопка Вставить;

· курсор в ячейку F8; кнопка Вставить;

· курсор в ячейку F9; кнопка Вставить.

В строке Меню установить указатель мыши на имя Сервис. В развернутом меню выбрать команду Поиск решения.

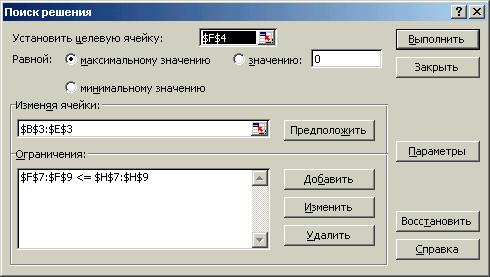
6. Назначим целевую функцию (установим целевую ячейку):

· курсор в строку Установить целевую ячейку;

· введем адрес ячейки $F$4;

· введем направление целевой функции в зависимости от условия задачи – Максимальному значению;

· курсор в строку Изменяя ячейки;

· введем адреса искомых переменных В$3:E$3.

7. Введем ограничения:

· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;

· в строке Ссылка на ячейку введем адрес $F$7: $F$9 (или укажем на листе, т.е. щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу, выделить ячейки F7:F9, нажать клавишу F 4, при этом ссылка станет абсолютной $F$7: $F$9, щелкнуть на красной стрелке и вернуться в блок Поиска решения, при этом нужный адрес будет введен);

· выберем знак ограничения <=;

· в строке Ограничения  введем адрес $Н$7: $Н$9;

· после введения ограничения кнопка ОК.

 

 

8. Введем параметры для решения ЗЛП:

· в диалоговом окне Поиск решения кнопка Параметры.

· на экране диалоговое окно Параметры поиска решения

· установим флажки:

ü Линейная модель (это обеспечит применение симплекс-метода)

ü Неотрицательные значения;

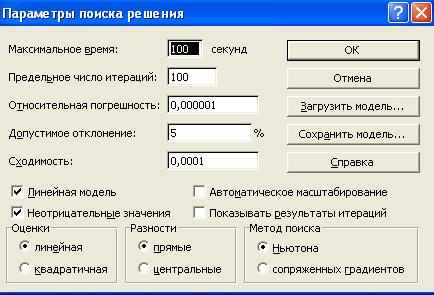
· кнопка ОК. На экране диалоговое окно Поиск решения;

· кнопку Выполнить.

· в диалоговом окно Результаты поиска решения

· выбрать Сохранить найденное решение

· кнопка OK

На экране представлена исходная таблица с заполненными ячейками ВЗ:ЕЗ для значений X и ячейка F4 с максимальным значением целевой функции. Введем экономическую интерпретацию полученных результатов: «Максимальный доход 1320 денежных единиц предприятие может получить при объемах выпуска продукции первого вида – 10 единиц, третьего вида – 6 единиц. Продукцию второго и четвертого вида выпускать не выгодно.»

Пример задачи целочисленного линейного программирования

Задача . Организация арендует баржу грузоподъёмностью 200 т. На этой барже предполагается перевозить груз 4 типов. Вес и стоимость единицы груза соответственно равны 20, 15, 20, 14 и 100, 80, 40, 30. Необходимо погрузить на баржу груз максимальной стоимости.

Экономико-математическая модель:

Введём необходимые обозначения: пусть x_j (j=1,2,3,4) – число предметов j-го типа, которое следует погрузить на баржу. Тогда ЭММ задачи о подборе для баржи допустимого груза максимальной стоимости запишется следующим образом:

max f(x₁, x₂, x₃, x₄) =100x₁+80x₂+40x₃+30x₄, 20x₁+15x₂+20x₃+14x₄ ≤ 200, x_j (j=1, 2, 3, 4) – целые неотрицательные.

Решение.

Необходимо последовательно выполнить следующие операции:

1. Создать текстовую форму-таблицу для ввода условий задачи и ввести исходные данные: 

2. Ввести зависимость для целевой функции:

· курсор в ячейку F4;

· кнопка Мастер функции;

· на экране появится диалоговое окно Мастер функций – шаг 1 из 2.

· выбрать на категорию Математические;

· выбрать функцию СУММПРОИЗВ;

· в строку Массив 1 ввести B$3:E$3;

· в строку Массив 2 ввести B4:E4;

· кнопка ОК.

3. Ввести зависимость для ограничений:

· скопировать полученную формулу в ячейку F8.

В строке Меню указатель мыши на Сервис. В развёрнутом меню команда Поиск решения. Появляется диалоговое окно  Поиск решения.

4. Назначим целевую функцию (установим целевую ячейку):

· курсор в строку Установить целевую ячейку;

· введем адрес ячейки $F$4;

· введем направление целевой функции в зависимости от условия задачи – Максимальному значению;

· курсор в строку Изменяя ячейки;

· введем адреса искомых переменных $B$3:$E$3.

5. Введите ограничения:

· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;

· в строке Ссылка на ячейку введем (или укажем на листе) адрес $F$8;

· выберем знак ограничения <=;

· в строке Ограничение введем адрес $H$8;

· кнопка Добавить

· в строке Ссылка на ячейку введем (или укажем на листе) адрес $B$3:$E$3;

· выберем значение цел   

 

· кнопка ОК.  

 

На экране появится диалоговое окно Поиск решения  с введёнными условиями.

6. Введем параметры для решения задачи:

· кнопка Параметры. 

· на экране диалоговое окно Параметры поиска решения;

· установим флажки:

ü Линейная модель (это обеспечит применение симплекс-метода)

ü Неотрицательные значения;

· кнопка ОК. 

· на экране появится диалоговое окно Поиск решения;

· кнопка Выполнить.

Появится диалоговое окно Результаты поиска решения.

· выберем Сохранить найденное решение

· кнопка ОК.   

 

Таким образом, рекомендуемое управленческое решение с позиций принятого критерия оптимизации – следует погрузить 1 предмет первого типа и 12 предметов второго типа. В этом случае стоимость груза составит 1060 у. е., и грузоподъёмность будет использована полностью.

Задачи для самостоятельного решения

1. Задача об оптимальном использовании ограниченных ресурсов. На участок строящейся дороги необходимо вывезти 20 000 м³ каменных материалов. В районе строительства имеются три карьера с запасами 8000м³, 9000 м³ и 10000 м³. Для погрузки материалов используются экскаваторы, имеющие производительность 250 м³/смену в карьерах А, Б и 500 м³/смену в карьере В. Эти карьеры обеспечивают каменными материалами также ряд других строящихся объектов. На погрузку материалов для рассматриваемого участка выделен для экскаваторов общий лимит 60 машино/смен с правом использовать его по усмотрению строителей. Транспортные затраты на перевозку материалов характеризуются следующими показателями: на перевозку 1000 м³ материалов из карьера А требуется 100 машино/смен, из карьера Б – 135 машино/смен, из карьера B – 170 машино/смен.

Требуется составить оптимальный план перевозок, обеспечивающий минимальные транспортные затраты.

2. Предлагается 5 инвестиционных проектов, тщательная экономическая экспертиза которых позволяет получить для каждого из проектов достаточно убедительные экономические оценки ожидаемого эффекта от их реализации 80; 50; 75; 40; 45 усл. ед. и необходимых капиталовложений 110; 60; 80; 15; 30 усл. ед. Общий объем возможных инвестиций ограничен величиной 200 усл. ед. Необходимо так распорядиться имеющимися финансовыми ресурсами, чтобы максимизировать суммарный эффект от инвестиций.

3. Задача о рациональном раскрое строительных материалов. Часть заемных оборотных средств предприятия иммобилизована в запасы пиломатериалов: на складе имеется партия бруса, содержащая 300 штук длиной 7,5 м каждый и партия бруса, содержащая 500 штук длиной 5 м каждый. Из этого материала можно изготовить оконные блоки, в каждый из которых входит две детали по 2,5 м и три детали длиной 2 м каждая. Как оптимально использовать заемные средства, если предположить, что спрос на оконные рамы неограничен?

Примеры задач транспортного типа

Задача . Перед менеджером нефтяной компании «Магнум» стоит задача создания схемы поставки нефтепродуктов от четырех нефтеперерабатывающих комплексов компании к пяти регионам страны. Одним из основных условий поставленной задачи является минимизация стоимости перевозок, при этом все мощности нефтеперерабатывающих комплексов должны бьть реализованы и все потребности регионов должны быть удовлетворены.

Мощности поставщиков и мощности потребителей, а также стоимость перевозок нефтепродуктов представлены в следующей таблице (в условных единицах).

Мощности поставщиков	Мощности потребителей
	600	400	700	500	1000
700	4	8	5	1	6
800	3	5	2	3	4
900	2	6	5	4	3
800	1	4	3	5	3

Решение.

В данном случае мощности поставщиков нефтепродуктов и потребности регионов в них совпадают, т.е. имеем дело с закрытой моделью транспортной задачи.

Ввод условий задачи состоит из следующих основных этапов.

1. Создание формы для решения задачи.

2. Ввод граничных условий.

3. Ввод исходных данных. 

4. Назначение целевой функции.

5. Ввод зависимостей из математической модели.

6. Ввод ограничений.

7. Просмотр результатов и печать отчета.

Рассмотрим более подробно каждый из этих этапов.

1. Создание формы для решения задачи предполагает создание матрицы перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек ВЗ:F6 заполняется значением 1. Таким образом, резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку груза (нефтепродуктов).

2. Ввод граничных условий.

Введение условия реализации мощностей  поставщиков, т.е.

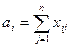
где a_i – мощность i -го поставщика;

x_{i , j} – объем поставки груза от i-го поставщика к j-му потребителю;

п – количество потребителей.

Для этого необходимо выполнить следующие операции:

· курсор в ячейку АЗ;

· кнопка Автосумма;

· выделить необходимые для суммирования ячейки ВЗ:FЗ;

· нажать ENTER – подтверждение ввода формулы для суммирования.

Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:

· курсор в АЗ;

· кнопка Копировать;

· выделить ячейки А4:А6;

· кнопка Вставить.

Введение условия удовлетворения запросов потребителей, т.е.

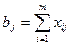
где b_j – мощность j -го потребителя;

т – количество поставщиков.

Для этого необходимо выполнить следующие операции:

· курсор в В7;

· кнопка Автосумма. При этом автоматически выделятся весь столбец ВЗ:В6;

· ЕNTER – подтверждение суммирования показателей выделенного столбца.

Последовательность этих действий выполнить для ячеек С7:F7, или же:

· курсор в В7;

· кнопка Копировать;

· выделить С7:F7;

· кнопка Вставить.

Таким образом, введены ограничения для всех поставщиков и всех потребителей.

3. Ввод исходных данных.

 

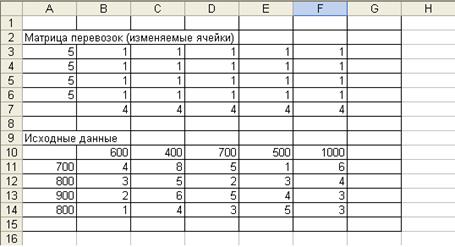
В конкретном примере осуществляется ввод мощностей четырех нефтеперерабатывающих предприятий (ячейки А11:А14), потребности регионов в их продукции (В10: F 10), а также удельные затраты по доставке нефтепродуктов от конкретного поставщика потребителю (блок В11: F 14).

4. Назначение целевой функции.

Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо в определенную ячейку ввести формулу для ее вычисления:

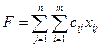
где c_ij – стоимость доставки единицы груза от i -го поставщика к j -му потребителю;

х _ij - объем поставки груза от i-го поставщика к j-му потребителю.

Для этого:

· курсор в ячейку В15. В данную ячейку будет помещаться значение целевой функции после решения задачи;

· кнопка Мастер функций;

На экране появится диалоговое окно Мастер функции шаг - 1 из 2

· выбрать категорию Математические;

· выбрать функцию СУММПРОИЗВ;

В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В11: F 14) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ: F 6). Для этого:

· в строку Массив 1 ввести В11:F14;

· в строку Массив 2 ввести ВЗ:F6;

· кнопка ОК.

В поле ячейки В15 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (число 77 в данной задаче).

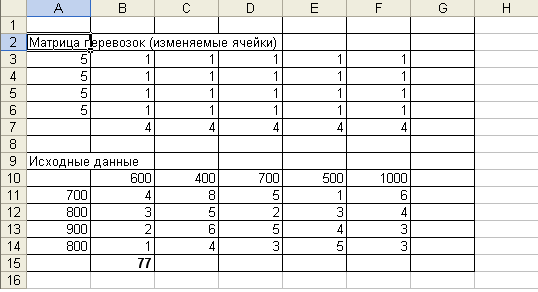
5. Ввод зависимостей из математической модели:

· выбрать Сервис ® Поиск решения;

· курсор в Установить целевую ячейку;

· ввести (выбрать) адрес $В$15.

Таким образом, производится указание ячейки, куда при решении задачи помещается значение целевой функции.

Или:

· поставить курсор в В15

· выбрать Сервис ® Поиск решения.

При этом осуществится автоматический ввод адреса $В$15 в поле адреса целевой ячейки;

· установить направление изменения целевой функции: минимальному значению.

Ввести адреса изменяемых ячеек ВЗ:F6. Для этого:

· щелкнуть в поле Изменяя ячейки;

· ввести адреса $В$3:$F$6 (или укажем на листе).

Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков. Для этого:

· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;

· в строке Ссылка на ячейку введем адреса (или укажем на листе) $А$3:$А$6;

· выберем знак ограничения =;

· в строке Ограничение введем адреса (или укажем на листе) $А$11:$А$14;

· кнопка OK

На экране появится диалоговое окно Поиск решения  с введённым условием.

Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей. Для этого:

· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;

· в строке Ссылка на ячейку введем адреса (или укажем на листе) $В$7:$F$7;

· выберем знак ограничения =;

· в строке Ограничение введем адреса (или укажем на листе) $В$10:$F$10;

· кнопка OK

6. Ввод ограничений.

Далее необходимо установить ограничения на решение задачи. Для этого:

· кнопка Параметры. 

· на экране диалоговое окно Параметры поиска решения:

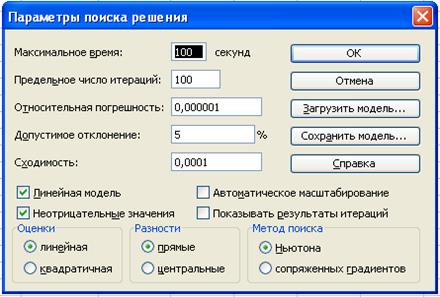
· установим флажки:

ü Линейная модель (это обеспечит применение симплекс-метода)

ü Неотрицательные значения, так как объемы поставок груза отрицательной величиной быть не могут;;

· кнопка ОК. 

· на экране появится диалоговое окно Поиск решения;

· кнопка Выполнить.

7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения

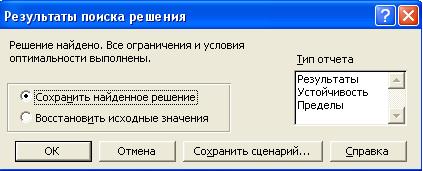
·  В окне Тип отчета выбрать интересующий вид отчета.

·  кнопка ОК.

Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.

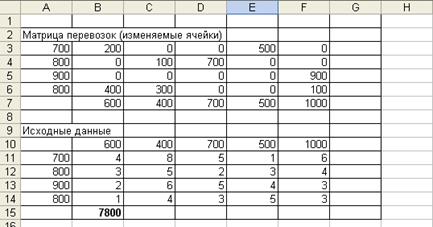
При нажатии Лист 1 происходит возврат в программу к исходным данным.

В матрице перевозок содержатся оптимальные объемы поставок грузов от поставщика потребителям, дающие минимум затрат на доставку. Значение целевой функции содержится в ячейке В15 и для конкретной задачи равно 7800. Из вышеизложенного можно сделать следующий вывод: минимум затрат на доставку нефтепродуктов, равный 7800 условных денежных единиц, будет обеспечен при следующем плане поставок:

1) от первого поставщика первому потребителю в объеме 2 (единиц и четвертому в объеме 500 единиц (условных);

2) от второго поставщика второму потребителю в объеме 18 единиц и третьему потребителю в объеме 700 единиц (условных);

3) от третьего поставщика пятому потребителю в объеме 900 единиц (условных);

4) от четвертого поставщика первому потребителю в объеме 400 единиц и второму потребителю в объеме 300 единиц (условных).

При данной схеме поставок мощности всех поставщиков будут реализованы и спросы всех потребителей будут удовлетворены.

 

Рассмотрим задачу о назначениях, которая в этом случае интерпретируется и реализуется как частный случай транспортной задачи.

 

Задача. На коммерческом предприятии имеется т работников А₁, А₂, ... А _i , …А_т, каждый из которых может выполнять одну из имеющихся т видов работ: В₁, В₂, ... В _j ,… В _m . Известно, что один и тот же работник может выполнять различные виды работ с разной производительностью труда (c_ij) в зависимости от опыта работы, квалификации, индивидуальны особенностей. В связи с этим возникает проблема распределений работников по должностям таким образом, чтобы производительность труда в коллективе была максимальной.

Экономико-математическая модель:

Обозначим через x_ij назначение i-го работника на j-должность. Так как количество работников равно количеству должностей и один работник может занимать только одну должность, то х _ij может принимать только два значения: 1 (если работник назначается на данную должность) или 0 (если не назначается). Тогда суммарная производительность труда работников (целевая функция) имеет следующий вид:

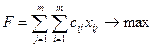
при ограничениях:

   

 

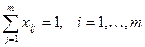
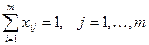
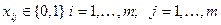
Умножая целевую функцию на -1, задача распределения по должностям может быть приведена к транспортной задаче, в которой объем запасов каждого поставщика и объем потребностей каждого потребителя равны 1.

 

Задача . Перед менеджером фирмы «Стар» стоит задача распределения четырех работников по вакантным должностям по условиям результатов контролых испытаний. Производительность труда по отдельным видам работ, показанная каждым из работников, приведена в таблице.

Одним из основных условий поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.

 

Работники	Производительность труда работников по должностям
	В1	В2	В3	В4
А1	3	1	5	2
А2	2	4	8	6
А3	8	2	7	6
А4	4	3	5	1

Решение.

Ввод условий задачи состоит из следующих основных этапов:

1. Создание формы для решения задачи.

2. Ввод граничных условий.

3. Ввод исходных данных.

4. Назначение целевой функции.

5. Ввод зависимостей из математической модели.

6. Ввод ограничений.

7. Просмотр результатов и печать отчета.

Рассмотрим более подробно каждый из этих этапов.

1. Создание формы для решения задачи предполагает создание матрицы назначений по должностям. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек ВЗ:Е6 вводятся «1». Таким образом, резервируется место, где после решения задачи будет находиться распределение рабочих по должностям, обеспечивающее максимальную производительность труда.

2. Ввод граничных условий.

Введение условия назначения работника только на одну должность, т.е.

,

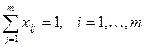где х _ij – назначение i-го работника на j-ую должность;

т – количество вакантных должностей

Для этого необходимо выполнить следующие операции:

· курсор в ячейку АЗ;

· кнопка Автосумма;

· выделить необходимые для суммирования ячейки ВЗ:EЗ;

· нажать ENTER – подтверждение ввода формулы для суммирования.

Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:

· курсор в АЗ;

· кнопка Копировать;

· выделить ячейки А4:А6;

· кнопка Вставить.

Введение условия заполнения вакантной должности, т.е.

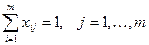
Для этого необходимо выполнить следующие операции:

· курсор в В7;

· кнопка Автосумма. При этом автоматически выделятся весь столбец ВЗ:В6;

· ЕNTER – подтверждение суммирования показателей выделенного столбца.

Последовательность этих действий выполнить для ячеек С7:F7, или же:

· курсор в В7;

· кнопка Копировать;

· выделить С7:F7;

· кнопка Вставить.

Таким образом, введены ограничения по назначению работника только на одну должность и условию заполнения всех вакантных мест.

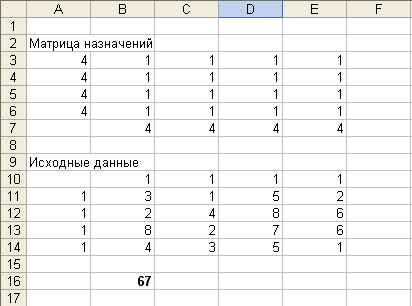
3. Ввод исходных данных.

В конкретном примере осуществляется ввод условной мощности работника фирмы (в ячейки А11:А14 вводится «1»), потребности в заполнении вакантной должности («1» - в В10:Е10), ввод производительности труда конкретного работника при проведении контрольных испытаний по каждой должности (блок В11:Е14).

4. Назначение целевой функции.

Для вычисления значения целевой функции, соответствующей максимальной суммарной производительности труда, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:

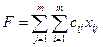
где c_ij – производительность труда i-го работника при занятии j-й должности;

х _ij – назначение i -го работника на j-должность. Для этого:

· курсор в ячейку В16. В данную ячейку будет помещаться значение целевой функции после решения задачи;

· кнопка Мастер функций;

На экране появится диалоговое окно Мастер функции шаг - 1 из 2

· выбрать на категорию Математические;

· выбрать функцию СУММПРОИЗВ;

В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В11: F 14) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ: F 6). Для этого:

· в строку Массив 1 ввести В11:F14;

· в строку Массив 2 ввести ВЗ:F6;

· кнопка ОК –  подтверждение окончания ввода адресов массивов

В поле ячейки В16 появится некоторое числовое значение равное произведению «1» на производительность каждого работника на конкретной должности (число 67 в данной задаче).

 5. Ввод зависимостей из математической модели.

Для осуществления этого этапа необходимо выполнить следующий перечень операций:

· поставить курсор в В16

· выбрать Сервис ® Поиск решения.

При этом осуществится автоматический ввод адреса $В$16 в поле адреса целевой ячейки;

· установить направление изменения целевой функции: минимальному значению.

Ввести адреса изменяемых ячеек ВЗ:E6. Для этого:

· щелкнуть в поле Изменяя ячейки;

· ввести адреса $В$3:$E$6 (или укажем на листе).

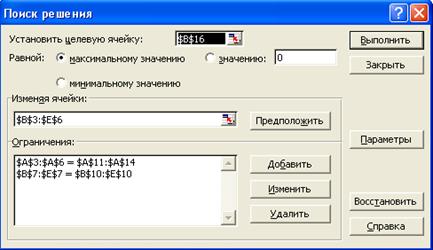
Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие назначения работника только на одну должность. Для этого:

· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;

· в строке Ссылка на ячейку введем адреса (или укажем на листе) $А$3:$А$6;

· выберем знак ограничения =;

· в строке Ограничение введем адреса (или укажем на листе) $А$11:$А$14;

· кнопка OK

На экране появится диалоговое окно Поиск решения  с введённым условием.

Далее вводится ограничение, которое реализует условие заполнения вакантной должности. Для этого:

· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;

· в строке Ссылка на ячейку введем адреса (или укажем на листе) $В$7:$E$7;

· выберем знак ограничения =;

· в строке Ограничение введем адреса (или укажем на листе) $В$10:$E$10;

· кнопка OK

6. Ввод ограничений.

Далее необходимо установить ограничения на решение задачи. Для этого:

· кнопка Параметры. 

· на экране диалоговое окно Параметры поиска решения:

· установим флажки:

ü Линейная модель (это обеспечит применение симплекс-метода)

ü Неотрицательные значения, так как значение работника на должность принимает значение «1» или «0» , т.е. отрицательной величиной быть не может;

· кнопка ОК. 

· кнопка Выполнить.

7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения

·  В окне Тип отчета выбрать интересующий вид отчета.

·  кнопка ОК.

Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.

При нажатии Лист 1 происходит возврат в программу, к исходным данным.

В Матрице назначений содержится схема распределения работников по должностям (1 – назначен, 0 – не назначен), дающая максимальную суммарную производительность труда, Значение целевой функции содержится в ячейке В16 и для конкретной задачи равно 22.

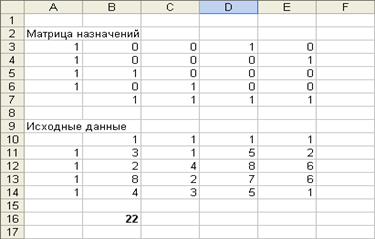
Вывод: максимум производительности труда, равный 22 условных единицы, будет достигнут при назначении:

1. первого работника на должность В₃ (содержимое ячейки D З = 1);

2. второго работника на должность В₄ (Е4=1);  

3. третьего работника на должность В₁ (В5=1);

4. четвертого работника на должность В₂ (С6=1).

Задачи для самостоятельного решения

1. Решите транспортную задачу, определив минимальную стоимость перевозки грузов

Мощности поставщиков	Мощности потребителей
	22	34	41	20
31	10	7	6	8
48	5	6	5	4
38	8	7	6	7

2. Перед менеджером стоит задача распределения четырех работников по вакантным должностям по условиям результатов контрольных испытаний. Производительность труда по отдельным видам работ, показанная каждым из работников, приведена в таблице.

Одним из основных условий поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.

 

Работники	Производительность труда работников по должностям
	В1	В2	В3	В4
А1	9	6	5	8
А2	4	8	6	2
А3	6	7	9	4
А4	2	7	3	1

Чему  равен максимум производительности труда?

3. Для строительства 4 дорог необходим гравий в количестве 130, 220, 60 и 70 единиц, который может быть поставлен из 3 карьеров, запасы которых составляют120,280 и 160 единиц соответственно, а тарифы перевозок представлены таблицей

1	7	9	5
4	2	6	8
3	7	1	2

Пример задачи нелинейной оптимизации

Задача. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4,10), (10,40), (40,80). Нижняя граница доходности портфеля задана равной 15.

Пример задачи, решаемой методом кусочно-линейной аппроксимации

Задача. Найти минимум функции 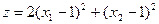 при ограничениях:

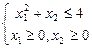
Решить данную задачу методом кусочно-линейной аппроксимации.

 

Решение.

Данная задача является задачей ВП. При условии неотрицательности переменных неравенство 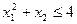 показывает, что  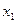может изменяться лишь от 0 до 2, а 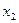– от 0 до 4.

Отрезок [0;2] разобьем точками 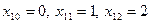, а отрезок [0;4] точками  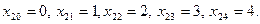Положим: .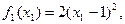

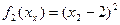Удобно сначала вычислить необходимые значения этих функций (т. к. имеем лишь одно ограничение, т. е. m=1, будем писать j ₁ и j ₂ вместо j ₁₁ иj ₁₂).

x1	x10	x11	x12		x2	x20	x21	x22	x23	x24
x1	0	1	2		x2	0	1	2	3	4
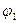
	0	1	4		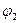	0	1	2	3	4
f1	2	0	2		f2	4	1	0	1	4

 

По формулам имеем:

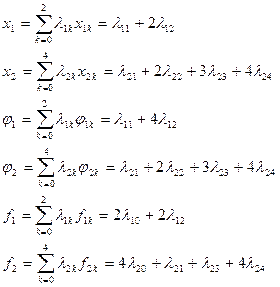
Таким образом, приближенная задача для данной задачи ВП имеет вид: найти минимум функции 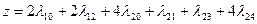  при ограничениях:

 

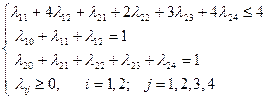
Решая данную задачу линейного программирования, как описано ранее, получим:

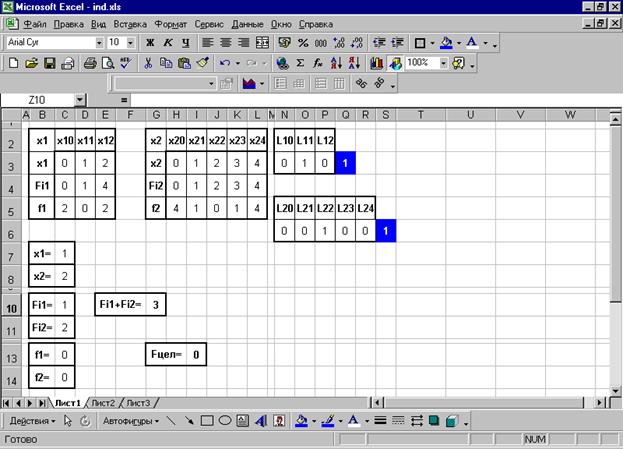
Таким образом, оптимальное решение приближенной задачи (1;2), и .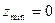

Задачи для самостоятельного решения

1 . Найти максимум функции 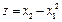 при ограничениях

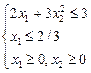
2. Найти минимум функции 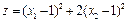 при ограничениях

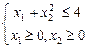
  3. Найти максимум функции 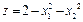 при ограничениях

    

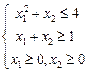
Пример задачи по теории игр, решаемой симплексным методом

Задача. Первый и второй игроки одновременно и независимо друг от друга показывают один, два или три пальца. Выигрыш или проигрыш (в денежных единицах) равен общему количеству показанных пальцев. Если это количество четное, то выигрывает первый игрок, а второй ему платит. Если же оно нечетное, то выигрывает второй игрок, а первый ему платит. Найти оптимальные стратегии каждого игрока.

 

Экономико-математическая модель

 У каждого игрока имеется по три стратегии: показать один, два или три пальца. В соответствии с этим платежная матрица будет выглядеть следующим образом:

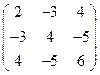
Выберем минимальные значения в каждой строке, а затем из них найдем максимальное. Это даст нам нижнюю цену игры. Она равна -3. Выберем максимальные значения в каждом столбце, а затем из них найдем минимальное. Получим верхнюю цену игры. Она равна 4. Так как нижняя цена игры не совпадает с верхней, то решение будем искать в смешанных стратегиях. Прибавляя ко всем элементам матрицы число, равное 5, перейдем к матрицы модифицированной игры:

,

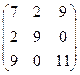которой соответствует задача линейного программирования для 1 игрока:

 min f(x₁, x₂, x₃) =x₁+x₂+x₃

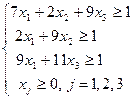
и задача линейного программирования для 2 игрока:

max f(x₁, x₂, x₃) =x₁+x₂+x₃

 

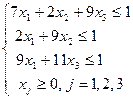
Решение.

Воспользовавшись симплексным методом, получим решения обеих задач, как описано ранее. Результаты приведены на рисунке.

 

 

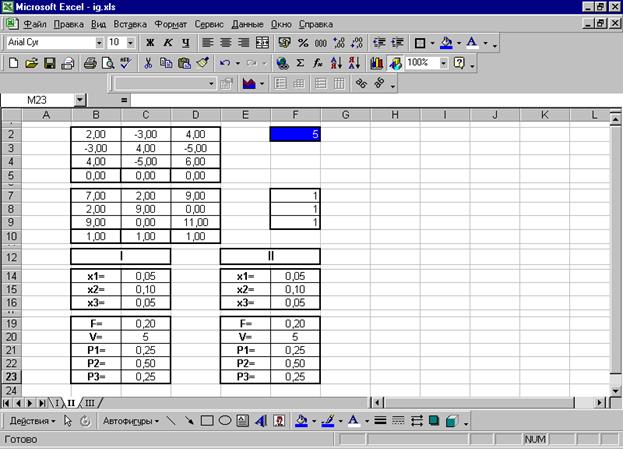
Таким образом, оптимальная смешанная стратегия 1-го игрока совпадает с оптимальной смешанной стратегией 2-го игрока и равна (0,25;0,5;0,25).

 

Задачи для самостоятельного решения

 

1. Найти оптимальную стратегию 1-го игрока для игры двух участников с нулевой суммой путем сведения ее к задаче линейного программирования, если задана платежная матрица:

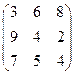
2. Найти оптимальную стратегию 2-го игрока для игры двух участников с нулевой суммой путем сведения ее к задаче линейного программирования, если задана платежная матрица:

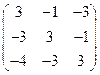
3. Найти оптимальные стратегии игроков для игры двух участников с нулевой суммой, если задана платежная матрица:

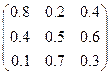
4. Найдите оптимальные стратегии игроков в известной игре «камень, ножницы, бумага».

Решение.

Обозначим через X_k количество средств, выделенных k-му предприятию. Суммарная прибыль равна . Переменные X удовлетворяют ограничениям:  Требуется найти переменные X₁, X₂, X₃, X₄, удовлетворяющие данным ограничениям и обращающие в максимум функцию Z.

Рассмотрим особенности модели. Ограничения линейные, но переменные целочисленные, а функции f_k(X_k) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.

Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств S₀=5 можно рассматривать как 4-шаговый, номер шага совпадает с номером предприятия; выбор переменных X₁, X₂, X₃, X₄ – уравнения соответственно на I, II, III, IV шагах; Ŝ - конечное состояние процесса распределения – равно нулю, так как все средства должны быть вложены в производство, Ŝ=0. Покажем схему распределения:

Уравнения состояний в данной задаче имеют вид:

S _k=S _k-1-X, (k= ),

где S_k-параметр состояния – количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися (4-k) предприятиями.

Введем в рассмотрение функцию Z_k^* (S_k-1) – условно оптимальную прибыль, полученную от k-го, (k+1)-го, ..., 4-го предприятий, если между ними распределялись оптимальным образом средства S_k-1 (0 £ S_k-1 £ 5). уравнения на k-ом шаге удовлетворяют условию: 0 £ X_k£S_k-1 (либо k-му предприятию ничего не выделяем, X_k=0, либо не больше того, что имеем к k-му шагу, X_k £ S_k-1 ).

 

Последовательно решаем уравнения

 проводя последовательную оптимизацию каждого шага. Для этого поступим следующим образом.

1. Создадим тексто­вую форму – таблицу для ввода условий задачи. Введем исходные данные задачи в созданную форму-таблицу:

2. В ячейку E15 введем формулу

=ИНДЕКС($B$3:$F$8; ПОИСКПОЗ($C15;$B$3:$B$8); G$12+1), скопируем формулу с ячейки E15 до ячейки Е35. 

3. В ячейку F15 введем формулу

=ИНДЕКС($B$3:$F$8;ПОИСКПОЗ($D15;$B$3:$B$8);5), скопируем формулу с ячейки F15 до ячейки F35.

4. В ячейку G15 введем формулу =E15+F15, скопируем формулу с ячейки G15 до ячейки G35.

5. Находим максимальное значение для каждого состояния от 0 до 5, для этого в ячейку Н15 введем формулу =МАКС(G15), после копирования формулы в ячейку H16, необходимо изменить диапазон с G16 на G16:G17, для этого стоя в строке формул необходимо растянуть выделенный прямоугольник на одну ячейку вниз. Затем копируем формулу из H16 в ячейку H18 и проводим такие же операции по увеличению диапазона, и т.д. до ячейки H30.

6. Находим значение управления Х_k, которому соответствует максимальное значение функции Z_k, для этого в ячейку I15 введем формулу =ИНДЕКС($C15:G15;ПОИСКПОЗ(H15;G15;0);1), скопируем формулу в ячейки I16, I18, I21, I25, I30 постепенно увеличивая диапазон, аналогично тому, как это делалось в пункте 5. В результате получим следующую таблицу:

7.  Выделяем диапазон ячеек E15:I35 выполняем команду Копировать, устанавливаем курсор в ячейку J15 выполняем команду Вставить.

8. Изменим формулу функции Z₃*(S₂). В ячейки K15, K16, K18, K21, K25, K30, введем соответственно максимальные значения предыдущего шага, находящиеся в ячейках H15, H16, H18, H21, H25, H30. В остальные ячейки поместим значения, стоящие в этом же столбце и соответствующие предыдущим S_k. В ячейку K17 копируем значение ячейки K15; в ячейки K19 и K20 – значения K16 и K17; в K22:K24 – K18:K20 и т. д. до ячейки K35. В результате получим:

 

9. Выделяем диапазон ячеек J15:N35 выполняем команду Копировать, устанавливаем курсор в ячейку O15 выполняем команду Вставить. В результате получаем заполненную таблицу:

10. Сравнивая полученные значения, получим Z₁^*(5)=24 усл. ед. = Z_max при X₁^*= X₁^*(5)=1. Вычисляя, получим S₁^* = 5 - 1 = 4, а по таблице в столбце 12 находим X₂^* = X₂^* (4) = 2. Далее находим S₂^* = 4-2 = 2, а в столбце 6 X₃^* = X₃^*(2) = 1. Наконец, S₃^* = 2-1 = 1 и X₄^*  = X₄^*(1) = 1, т. е. X^*(1; 2; 1; 1).

  Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию – 2 усл. ед.; 3-му предприятию – 1 усл. ед.; 4-му предприятию – 1 усл. ед.

 

Задачи для самостоятельного решения

 

1. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S₀=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k–му предприятию (k=1, 2, 3, 4), приносит в конце года прибыль f_k(X). Функции f_k(X) заданы таблично:

Х	f1(X)	f2(X)	f3(X)	f4(X)
1 2 3 4 5	0,2 0,9 1,0 1,2 2,0	1,0 1,1 1,3 1,4 1,8	2,1 2,5 2,9 3,9 4,9	0 2,0 2,5 3,0 4,0

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.

2. Планируется деятельность трех промышленных предприятий на очередной год. Начальные средства: S₀=9 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k–му предприятию (k=1, 2, 3), приносит в конце года прибыль f_k(X). Функции f_k(X) заданы таблично:

Х	f1(X)	f2(X)	f3(X)
1 2 3 4 5 6 7 8 9	5 9 12 14 15 18 20 24 27	7 9 11 13 16 19 21 22 25	6 10 13 15 16 18 21 22 25

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.

 

ЛИТЕРАТУРА

1. Акоф, Р., Сасиени, М. Основы исследования операций. / Пер. с англ. Под ред. И. А. Ушакова. М.: Мир., 1971.- 536 с.
2. Волков, И.К., Загоруйко, Е.А. Исследование операций: учебник для вузов. М.: МГТУ им. Н. Э. Баумана. 2000. - 436 с.
3. Добрынина, И.В. Исследование операций: учебно-методическое пособие. Тула: ТГУ. 2002. - 120 с.
4. Додж, М., Стинсон, К. Эффективная работа с Microsoft Excel 2000. – СПб.: Питер, 2002. – 1056 с.
5. Кремер, Н.Ш. Исследование операций в экономике: учебное пособие для вузов. М.: ЮНИТИ. 1997. - 407 с.
6. Курицкий, Б.Я. Поиск оптимальных решений средствами MS Excel 7.0. С.-П. BHV.1997.-384 с.
7. Экономико-математические методы и прикладные модели: компьютерный практикум. М.: ИНФРА, –М. 2002. – 72 с.

 

И. В. Добрынина, Р. Р. Яфаева

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО