Блок «Высшая математика».
Понятие матриц. Виды матриц.
Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 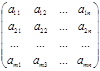
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида:
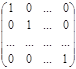 = E,
= E,
называется единичной матрицей.
Определение. Если amn = anm , то матрица называется симметрической.
Пример . 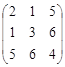 - симметрическая матрица
- симметрическая матрица
Определение. Квадратная матрица вида 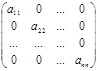 называется диагональной матрицей.
называется диагональной матрицей.
Определители. Вычисление определителей.
Определителем квадратной матрицы А= 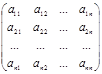 называется число, которое может быть вычислено по элементам матрицы по формуле:
называется число, которое может быть вычислено по элементам матрицы по формуле:
det A =  , где
, где
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det A = 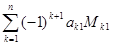
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA = 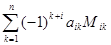 , i = 1,2,…,n.
, i = 1,2,…,n.
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Обратная матрица.
Определим операцию деления матриц как операцию, обратную умножению.
Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E Þ 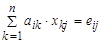 , i=(1,n), j=(1,n),
, i=(1,n), j=(1,n),
eij = 0, i ¹ j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
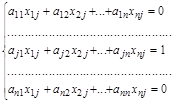 ,
,
Решив эту систему, находим элементы матрицы Х.
Пример. Дана матрица А = 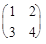 , найти А-1.
, найти А-1.
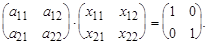
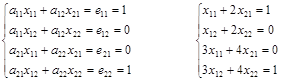
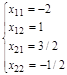
Таким образом, А-1= 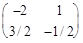 .
.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
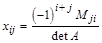 ,
,
где Мji- дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = 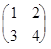 , найти А-1.
, найти А-1.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1= 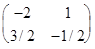 .
.
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Определение. Если 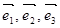 - базис в пространстве и
- базис в пространстве и 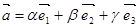 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора 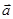 в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
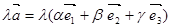 =
= 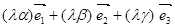 .
.
- при сложении векторов складываются их соответствующие компоненты.
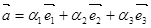 ;
; 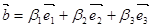 ;
;
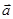 +
+ 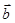 =
= 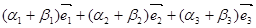 .
.
Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то 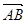 = (x2 – x1, y2 – y1, z2 – z1).
= (x2 – x1, y2 – y1, z2 – z1).
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то 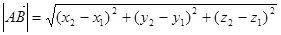 .
.
Если точка М(х, у, z) делит отрезок АВ в соотношении l / m, считая от А, то координаты этой точки определяются как:
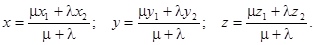
В частном случае координаты середины отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Линейные операции над векторами в координатах.
Пусть заданы векторы в прямоугольной системе координат
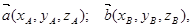 тогда линейные операции над ними в координатах имеют вид:
тогда линейные операции над ними в координатах имеют вид:
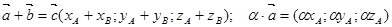
Примеры.
Пусть А(-1; 1; 0), B(3; 1; -2), 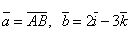 . Найти:
. Найти:
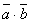 ;
;
 и
и 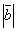 ;
;
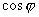 .
.
a. 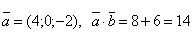 .
.
b. 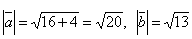 .
.
c. 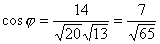 .
.
Основные свойства функций.
1. Четность и нечетность
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
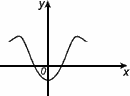
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)

График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом 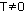 , если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
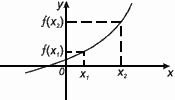
3. Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
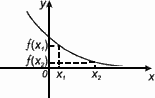
Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
4. Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х) 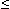 f(Xmax).
f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.
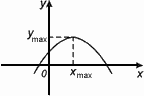
Хmax – точка максимума
Уmax – максимум
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х) 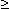 f(Xmin).
f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
Xmin – точка минимума
Ymin – минимум
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
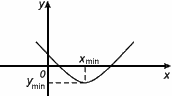
5. Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
Х1,Х2,Х3 – нули функции y = f(x).
Пример 1
Найти производную функции у=С, С=const.
Решение:
- Значению х даем приращение ∆х;
- находим приращение функции ∆у: ∆у=ƒ(х+∆х)-ƒ(х)=С-С= 0;
- значит, ∆(y)/ ∆(x)=0/∆(x)=0;
- следовательно,
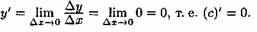
Пример 2
Найти производную функции у=х2.
Решение:
- Аргументу х даем приращение ∆х;
- находим ∆у: ∆у=(х+∆х)2—х2=2х•∆х+(∆х)2;
- составляем отношение
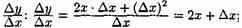
- находим предел этого отношения:
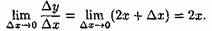
Таким образом, (х2)'=2х.
В задаче про скорость прямолинейного движения было получено
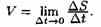
Это равенство перепишем в виде V=S't, т. е. скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t. В этом заключается механический смысл производной.
Обобщая, можно сказать, что если функция y=f(x) описывает какой-либо физический процесс, то производная у' есть скорость протекания этого процесса. В этом состоит физический смысл производной.
В задаче про касательную к кривой был найден угловой коэффициент касательной
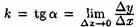
Это равенство перепишем в виде
ƒ'(х) = tga = k,
т. е. производная ƒ'(х) β точке х равна угловому коэффициенту касательной к графику функции у = ƒ(х) в точке, абсцисса которой равна х. В этом заключается геометрический смысл производной.
Таблица дифференциалов



Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 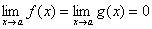 или
или 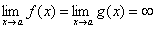 . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций 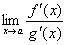 , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
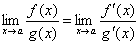 (1)
(1)
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти 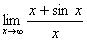 . Этот предел существует
. Этот предел существует 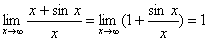 . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Примеры.
1. 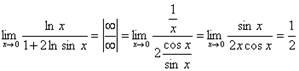 .
.
2. 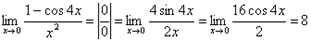 .
.
3. 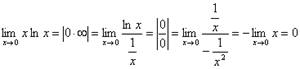 .
.
Дробно-линейная подстановка
Интегралы типа 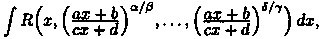 где а, b, с, d - действительные числа, a,b,...,d,g - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки
где а, b, с, d - действительные числа, a,b,...,d,g - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки  где К - наименьшее общee кратное знаменателей дробей
где К - наименьшее общee кратное знаменателей дробей 
Действительно, из подстановки  следует, что
следует, что 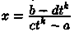 и
и

т. е. х и dx выражаются через рациональные функции от t. При этом и каждая степень дроби  выражается через рациональную функцию от t.
выражается через рациональную функцию от t.
Пример Найти интеграл 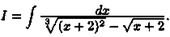
Решение: Наименьшее общee кратное знаменателей дробей 2/3 и 1/2 есть 6.
Поэтому полагаем х+2=t6, х=t6-2, dx=6t5 dt, 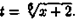 Следовательно,
Следовательно,
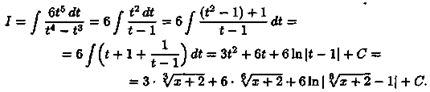
Пример Указать подстановку для нахождения интегралов:
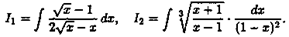
Решение: Для I1 подстановка х=t2, для I2 подстановка 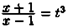
Интегрирование по частям
Теорема. Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула
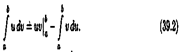 2.
2.
На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:
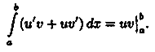
Следовательно,
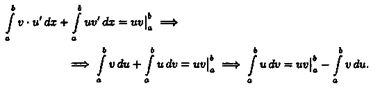
Формула (.2) называется формулой интегрирования по частям для определенного интеграла.
Пример. Вычислить 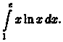
Решение: Положим

Применяя формулу 2), получаем

Пример.
(х + у)×у/ = 1.
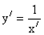 ,
, 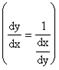 .
.
Пусть
x = u×v, тогда 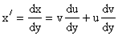 и
и
v×u/ + u×v/ = x + y.
Учитывая, что х = u×v, имеем
v×(u/-v) + u×v/ = y
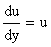 следовательно, lnu = y, u = ey,
следовательно, lnu = y, u = ey,
Так как 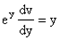 , то имеем
, то имеем 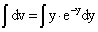 .
.
Далее
v = -y×e-y - e-y + C.
x = u×v = -y-1 + C×ey - общее решение.
y = -y-1 + C×ey
начальные условия:
у0 = 0, х0 = 2.
2 = -1 + С Þ С = 1
х + у + 1 = еу - частное решение.
Признаки сравнения
Если 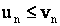 , и ряд
, и ряд 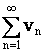 сходится, то сходится и ряд
сходится, то сходится и ряд 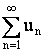 .
.
Если  , и ряд
, и ряд 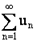 расходится, то расходится и ряд
расходится, то расходится и ряд 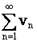 .
.
Признаки сравнения можно сформулировать в такой форме:
Если заданы ряды 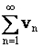 ,
, 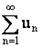 и существует
и существует 
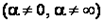 , то ряды
, то ряды 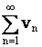 и
и 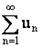 сходятся либо расходятся одновременно.
сходятся либо расходятся одновременно.
Пример:
1. Исследуем сходимость ряда 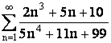 . Очевидно, что
. Очевидно, что 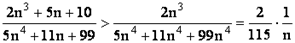 .
.
Так как гармонический ряд 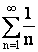 расходится, то и ряд
расходится, то и ряд 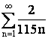 также расходящийся, и, согласно признаку сравнения, данный ряд
также расходящийся, и, согласно признаку сравнения, данный ряд 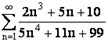 расходится.
расходится.
2. Исследовать сходимость ряда 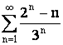 . Имеем:
. Имеем: 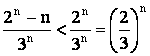 .
.
Ряд 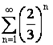 сходится как сумма геометрической прогрессии со знаменателем
сходится как сумма геометрической прогрессии со знаменателем 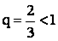 . Следовательно, согласно признаку сравнения ряд
. Следовательно, согласно признаку сравнения ряд 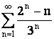 сходится.
сходится.
Признак Д’Аламбера
Если существует 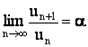 то:
то:
- при 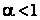 ряд
ряд 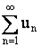 сходится;
сходится;
- при 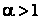 ряд
ряд 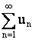 расходится.
расходится.
Радикальный признак Коши
Если существует 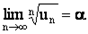 то:
то:
- при 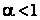 ряд
ряд 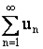 сходится;
сходится;
- при 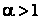 ряд
ряд 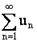 расходится.
расходится.
Интегральный признак Коши
Пусть задан ряд 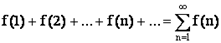 , члены которого являются значениями непрерывной, положительной и монотонно убывающей функции
, члены которого являются значениями непрерывной, положительной и монотонно убывающей функции 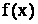 на промежутке
на промежутке 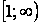 . Тогда ряд
. Тогда ряд 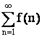 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл 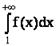 .
.
Если же 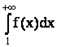 расходится, то ряд
расходится, то ряд 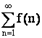 также будет расходящимся.
также будет расходящимся.
Доказательство.
Лемма. Пусть 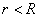 . Тогда
. Тогда 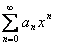 сходится на множестве
сходится на множестве 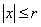 абсолютно и равномерно.
абсолютно и равномерно.
Доказательство. Так как 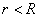 , ряд
, ряд 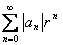 сходится. Так как
сходится. Так как 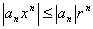 , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
, можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
Замечание. Лемма отнюдь не утверждает равномерной сходимости степенного ряда на 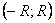 . Да это, вообще говоря, и неверно. Например, прогрессия
. Да это, вообще говоря, и неверно. Например, прогрессия 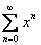 сходится на
сходится на 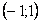 неравномерно. Однако этот ряд сходится равномерно на любом
неравномерно. Однако этот ряд сходится равномерно на любом 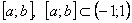 .
.
Пусть теперь 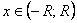 , т.е.
, т.е. 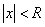 . Выберем
. Выберем 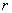 так, чтобы
так, чтобы 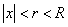 . Тогда, по доказанной лемме, ряд сходится на
. Тогда, по доказанной лемме, ряд сходится на 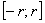 абсолютно и равномерно. Поскольку все функции
абсолютно и равномерно. Поскольку все функции 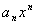 - непрерывные, сумма ряда есть непрерывная на
- непрерывные, сумма ряда есть непрерывная на 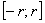 функция. Значит, эта функция непрерывна и в выбранной, произвольной точке
функция. Значит, эта функция непрерывна и в выбранной, произвольной точке 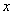 интервала
интервала 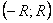 .
.
Следствие. (Единственность степенного ряда). Пусть 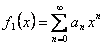 ,
, 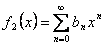 и в некоторой окрестности
и в некоторой окрестности 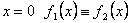 . Тогда
. Тогда 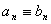 .
.
Доказательство. При 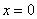 получаем:
получаем: 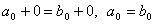 . Поэтому
. Поэтому 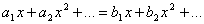 . При
. При 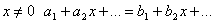 . В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при
. В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при 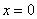 , откуда
, откуда 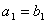 и т.д. (Отметим, что здесь существенно использована непрерывность ряда в точке
и т.д. (Отметим, что здесь существенно использована непрерывность ряда в точке 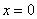 ).
).
Сформулируем без доказательства еще одну важную теорему.
Теорема. (Абель). Если ряд 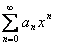 , имеющий сумму
, имеющий сумму 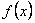 , сходится (хотя бы неабсолютно) при
, сходится (хотя бы неабсолютно) при 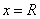 , то
, то 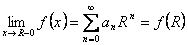 (т.е. сумма ряда непрерывна слева).
(т.е. сумма ряда непрерывна слева).
Теорема. Для любого 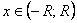
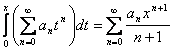 .
.
Доказательство. Пусть 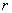 удовлетворяет неравенствам
удовлетворяет неравенствам 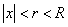 . Тогда степенной ряд сходится равномерно на
. Тогда степенной ряд сходится равномерно на 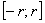 и его можно почленно проинтегрировать. Кроме того,
и его можно почленно проинтегрировать. Кроме того, 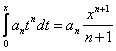 . Теорема доказана.
. Теорема доказана.
Теорема. Для любого 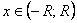
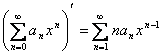 .
.
Доказательство. Выберем 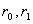 так, чтобы
так, чтобы 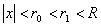 . По определению
. По определению 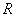 , ряд
, ряд 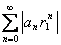 сходится. Поэтому
сходится. Поэтому 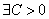 (см. доказательство теоремы 1):
(см. доказательство теоремы 1): 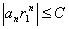 . Рассмотрим величину
. Рассмотрим величину 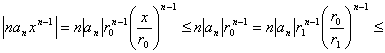
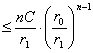 . По признаку Даламбера, ряд
. По признаку Даламбера, ряд 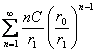 сходится, т.к.
сходится, т.к.  . Значит, мы оценили члены ряда
. Значит, мы оценили члены ряда 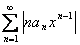 при
при 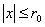 членами сходящегося ряда
членами сходящегося ряда 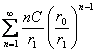 . Применяя теорему Вейерштрасса на
. Применяя теорему Вейерштрасса на 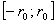 , получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке
, получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке 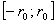 , а значит, и в точке
, а значит, и в точке 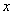 . Ввиду произвольности точки
. Ввиду произвольности точки 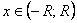 , теорема доказана.
, теорема доказана.
Важное замечание. Из доказанных теорем вытекает, что при интегрировании и дифференцировании радиус сходимости не уменьшается. Но увеличиться он также не может. Если бы, например, он увеличился и стал равен 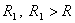 при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем
при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем 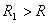 (по доказанному).
(по доказанному).
Итак, радиус сходимости степенного ряда не меняется при почленном интегрировании и дифференцировании.
Однако поведение в концевых точках 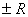 может меняться. Например, ряд
может меняться. Например, ряд 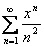 сходится на
сходится на 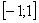 . При этом ряд
. При этом ряд 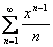 , получающийся из исходного дифференцированием, сходится только на
, получающийся из исходного дифференцированием, сходится только на 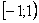 , а прогрессия
, а прогрессия 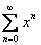 , получающаяся при дифференцировании ряда
, получающаяся при дифференцировании ряда 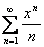 (сходящегося на
(сходящегося на 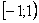 ), сходится на
), сходится на 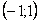 .
.
Рассмотрим теперь функцию 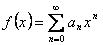 , представляемую степенным рядом в области его сходимости. Очевидно,
, представляемую степенным рядом в области его сходимости. Очевидно, 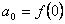 . Далее, последовательно применяем теорему о почленном дифференцировании ряда.
. Далее, последовательно применяем теорему о почленном дифференцировании ряда. 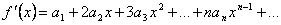 , откуда
, откуда 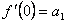 .
. 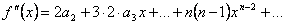 , откуда
, откуда 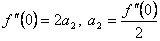 .
. 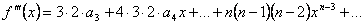 ,
, 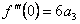 и т.д.
и т.д. 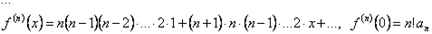 .
.
Следовательно, при всех 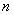
 . Таким образом,
. Таким образом, 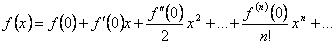 . Это можно сформулировать так: степенной ряд, сходящийся к
. Это можно сформулировать так: степенной ряд, сходящийся к 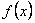 , представляет собой ряд Тейлора для своей суммы
, представляет собой ряд Тейлора для своей суммы 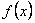 .
.
Если 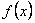 имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке 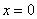 , то можно образовать соответствующий ей ряд Тейлора:
, то можно образовать соответствующий ей ряд Тейлора: 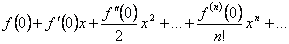 .
.
Важное замечание. Не всегда этот ряд сходится к самой функции 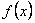 . Например, нетрудно доказать, что функция
. Например, нетрудно доказать, что функция 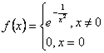 имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке 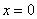 и все они равны 0, т.е.
и все они равны 0, т.е. 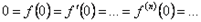 . Ряд Тейлора этой функции тождественно равен 0 и не совпадает с
. Ряд Тейлора этой функции тождественно равен 0 и не совпадает с 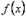 .
.
Необходимое и достаточное условие для того, чтобы ряд Тейлора функции 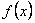 сходился к самой функции
сходился к самой функции 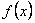 , можно сформулировать так: остаток
, можно сформулировать так: остаток 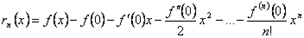 должен стремиться к 0 при
должен стремиться к 0 при 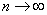 .
.
Блок «Высшая математика».
Понятие матриц. Виды матриц.
Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 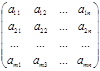
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида:
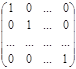 = E,
= E,
называется единичной матрицей.
Определение. Если amn = anm , то матрица называется симметрической.
Пример . 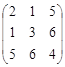 - симметрическая матрица
- симметрическая матрица
Определение. Квадратная матрица вида 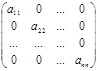 называется диагональной матрицей.
называется диагональной матрицей.
Дата: 2019-12-22, просмотров: 230.