Часто нет необходимости строить функцию распределения, а достаточно найти некоторые ее числовые характеристики.
Основные из них:
Математическое ожидание (M[x]; mx) – сумма произведений значений СВ на соответствующие вероятности
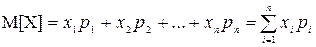 ( для ДСВ)
( для ДСВ)
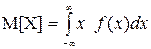 (для НСВ)
(для НСВ)
Замечание: сумма и интеграл – конечны.
Геометрически математическое ожидание это – абсцисса центра тяжести площади под кривой распределения.
Дисперсия СВ D[Х] – это мера рассеяния СВ вокруг ее математического ожидания (центра тяжести).
D [X]= М[x - m x]2 = 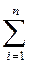 ( x i – mx)2 рi для ДСВ
( x i – mx)2 рi для ДСВ
D [X]= 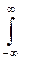 ( x -m x)2 f(x)d x для НСВ
( x -m x)2 f(x)d x для НСВ
Средним квадратическим отклонением СВ Х называется корень квадратный из дисперсии: G[Х]=Gх= 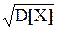 .
.
Модой ДСВ Х называется ее наиболее вероятное значение. Для НСВ Х мода – это значение случайной величины Х, при котором плотность ее распределения максимальна. Обозначают M0; Xмо.
Медиана – такое значение x СВ Х, относительно которого равновероятно получение большего или меньшего ее значения.
Обозначают Me, Xmе.
P(x<Xме)=P(x>Xме)
Замечание: ордината, проведенная в т Xme делит площадь под кривой плотности распределения пополам. В случае дискретной случайной величины при четном числе xi, медиана находится как полусумма двух средних значений.
Пример 25. Баскетболисту предоставляется четыре попытки забросить мяч в корзину. Вероятность попадания при одном бросании 0,6.
Найти:
1.Закон распределения числа попаданий в корзину.
2. Функцию распределения F(x) и построить ее график.
3. Вероятность попадания случайной величины в интервал (0,5;3] двумя
способами.
4. Математическое ожидание числа попаданий мяча в корзину, дисперсию,
среднее квадратическое отклонение, моду, медиану.
Решение.
Пусть СВ Х-число попаданий при четырех бросаниях мяча. Тогда она может принимать значения: х1=0; х2=1; х3=2; x4=3; x5=4
Вероятность попасть при одном бросании р=0,6; вероятность промаха q=1–р=0,4. Найдем вероятности, соответствующие различным значениям СВ Х. Для этого воспользуемся формулой Бернулли: 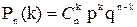
x1=0, Р4(0)=C40×р0×q4=1×1×(0,4)4»0,02
х2=1, Р4(1)=C41×р1×q3=4×0,6×(0,4)3»0,15
х3=2, Р4(2)=C42×р2×q2=6×(0,6)2×(0,4)2»0,35
х4=3, Р4(3)=C43×р3×q1=4×(0,6)3×0,4»0,35
х5=4, Р4(4)=C44×р4×q0=1×(0,6)4×1»0,13
1. Составим ряд распределения:
xi< xi+1, (i=1,..,5)
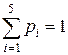
|
| x | 0 | 1 | 2 | 3 | 4 |
| p | 0,02 | 0,15 | 0,35 | 0,35 | 0,13 |
Построим многоугольник распределения:
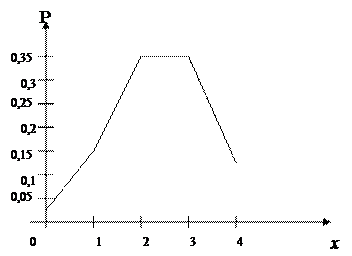 |
2. Найдем функцию распределения и построим ее график :
F(x)= 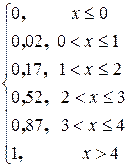
| 
|
3. Вычислим вероятность попадания в заданный интервал двумя способами:
а) P(0,5<X £3)=F(3)-F(0,5)=0,52-0,02=0.5
б) P(0,5<X £3)=P(x=1)+P(x=2)=0,15+0,35=0.5
4. Найдем числовые характеристики CBX
Математическое ожидание
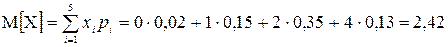
Дисперсия
D[X]=M[X2]–M2[X]
M[X2]= 0×0,02+1×0,15+4×0,35+9×0,35+16×0,13=6,78
M2[X]=2,42 2 =5,85
D[X]=6,78–5,85=0,93
Среднее квадратическое отклонение
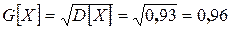
Мода
Mo=2 Mo=3 p(2)=p(3)=0,35
Медиана
Me = 2, т.к. слева и справа от x=2 равное количество значений признака.
Пример 26. Распределение непрерывной случайной величины задано функцией плотности
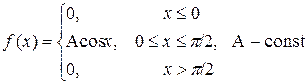
Найти:
1. Интегральную функцию распределения CBX - F(x).
2. Построить графики f(x) и F(x).
3. Найти вероятность попадания CBX в интервал 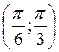 двумя
двумя
способами (через f(x) и F(x)).
4. Найти числовые характеристики CBX: M[X], D[X], G[X], Mo, Me.
Решение.
Найдем А: 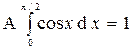 ;
; 
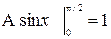 A=1, тогда
A=1, тогда
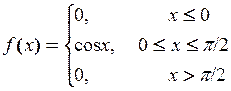
Найдем интегральную функцию распределения
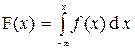
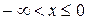
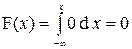
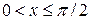
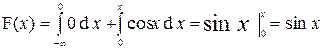
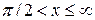
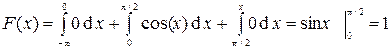
Итак,
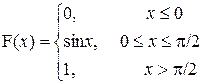
2. Построим графики функций f(x) и F(x)
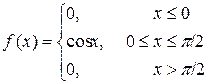
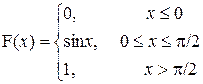
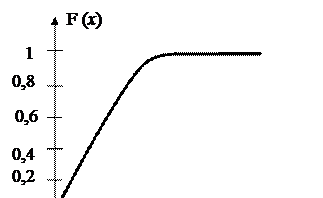 | |||
 | |||
3. Вычислим вероятность попадания CB X в заданный интервал двумя
способами.
а) 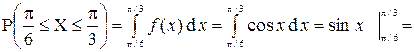
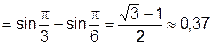
б) 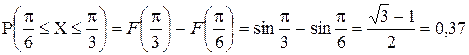
4. Найдем чиcловые характеристики CB X:
Математическое ожидание
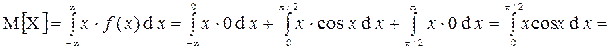
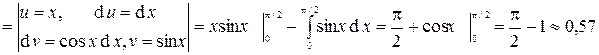
Дисперсия
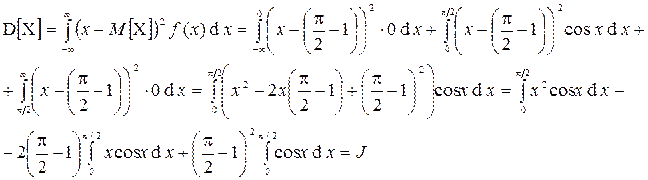
Вычислим каждый интеграл отдельно
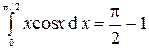 (вычислен ранее)
(вычислен ранее)
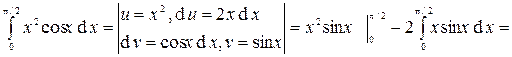
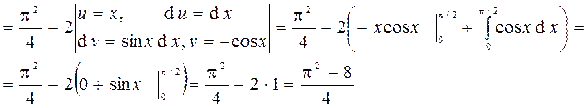
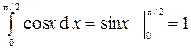
Итак 

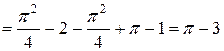
Среднее квадратичное отклонение
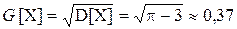
Мода
x=0, т.к. f(x)=f(0)=cos0=1 – max.
Медиана
а) 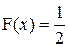 , т.е.
, т.е. 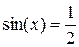
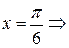
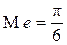
б) Пусть Me = x0
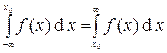 ; x0 не лежит вне интервала
; x0 не лежит вне интервала 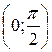 , т.к. там f(x)=0, поэтому
, т.к. там f(x)=0, поэтому
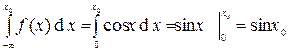
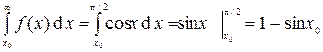
sin x0=1–sin x0; 2sin x0=1; 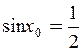
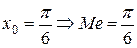
Условия к практическим заданиям
Задание 1: Задана дискретная случайная величина Х рядом распределения или задача, по содержанию которой он может быть составлен.
Требуется:
Найти функцию распределения F(x) и построить ее график.
Вычислить вероятность попадания случайной величины Х в заданный интервал (а,b) двумя способами.
Найти числовые характеристики случайной величины Х: математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану.
Задание 2: Непрерывная случайная величина Х задана функцией распределения F(x) (для четных вариантов) или функцией плотности f(x) (для нечетных вариантов).
Требуется:
Найти функцию плотности f(x) (для четных вариантов) или функцию распределения F(x) (для нечетных вариантов).
Построить их график.
Вычислить вероятность попадания случайной величины Х в заданный интервал (а,b) двумя способами.
Найти числовые характеристики случайной величины Х: математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану.
Задания
1. a) Пассажир делает три попытки купить билет на поезд, причем вероятность того, что он купит билет с одной попытки равна 0,7. Составить закон распределения числа попыток купить билет.
P(1£ X £2)
 b)
b)
| a=1; b=2 |
2. a) Проводится 4 независимых испытания рессоры для вагона. Вероятность благополучно пройти одно испытание равна 0,8. Составить закон распределения испытаний, которые рессора пройдет благополучно.
P (2<X<4)
b)
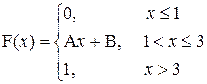
| a=1,5; b=2 |
3. a) Управление вагоно-ремонтного завода выпустило 100 новогодних лотерейных билетов для работников завода достоинством 10 руб. —50 шт., 50 руб. —20 шт., 70 руб. —10 шт., 100 руб. — 1шт.
Остальные билеты невыигрышные. Составить закон распределения стоимости выигрыша владельцем одного лотерейного билета.
P(50< X £100)
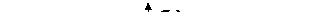 b)
b)
| a= –2,5; b= –1 |
4. a)
| x | –2 | –1 | 0 | 1 | 2 |
| p | 0,1 | 0,2 | 0,3 | p | 0,15 |
P(–2< X £ 0)
b)
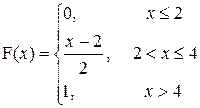
| a =3; b=2,5 |
5. а) В магазин поступили учебники по 3м дисциплинам математике, физике, теории вероятностей. Студент намерен приобрести 3 разных учебника. Вероятность купить любой из них равна 0,6. Пусть Х – число различных учебников, купленных студентом. Составить закон распределения чисел купленных книг.
Р(0 £ Х < 2)
 b)
b)
| a= –2; b= –1 |
6. a) В математической олимпиаде предлагается решить 5 задач. Студент решает любую задачу с вероятностью 0,8. Составить закон распределения числа решенных задач.
P (3£ X £5)
b)
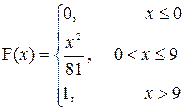
| a=3; b=5 |
7. a) В цехе завода производят оси вагонных колес. В партии из 6 пронумерованных осей 1 бракованная. Брак выявляют, проверяя одну ось за другой, выбирая их наудачу. Найти закон распределения номера выбранной для проверки оси, включая бракованную.
P (1<X<3)
 b)
b)
| a=2; b=¥ |
8. a) Товарная станция имеет контейнеры различного тоннажа для перевозки груза: 1,5 т, 3 т, 5 т и 7 т. Она выделяет заказчику один контейнер. Составить ряд распределения тоннажа выделенного заказчику контейнера.
P (1<X<3)
b)
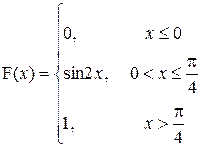
|
a=0; b= 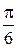
|
9. a) Деталь проходит три этапа контроля. Вероятность нахождения дефекта на первом этапе p1=0,2; на втором – p2=0,3; на третьем – p3=0,1. X – число случаев нахождения дефекта. Составить закон распределения случайной величины X.
P (0≤X<2)
 b)
b)
| a=1,5; b=3 |
10. a) Пассажиру надо купить в железнодорожной кассе 3 билета на поезда трех разных назначений. Вероятность купить билет на поезд 1-ого назначения p1=0,8; на поезд 2-ого назначения p2=0,7; на поезд 3-его назначения p3=0,6. Пусть X – число случаев приобретения пассажиром билетов. Найти закон распределения случайной величины X.
P (1≤X<3)
b)
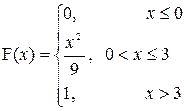
| a=1; b=4 |
11. a) На пути из города A в город B поезд проходит 5 светофоров. Каждый из них разрешает проезд или запрещает. Пусть X – число светофоров, пройденных поездом до первой остановки. Найти закон распределения случайной величины X.
P (X>2)
b)

| a=0; b=1,8 |
12. a) Вагоно-ремонтный завод выпускает в месяц 60% пассажирских вагонов и 40% – товарных. Наудачу берут для контроля качества ремонта 5 вагонов. Пусть X – число пассажирских вагонов. Составить закон распределения случайной величины X.
P (2<X≤ 5)
b)
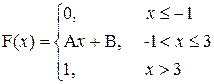
| a = 0; b=2 |
13. a) 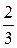 всех сотрудников заводоуправления имеет высшее образование и
всех сотрудников заводоуправления имеет высшее образование и 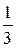 средне-техническое. Отбираются наудачу 5 человек. Составить закон распределения числа сотрудников с высшим образованием.
средне-техническое. Отбираются наудачу 5 человек. Составить закон распределения числа сотрудников с высшим образованием.
P(2<X<3)
b)
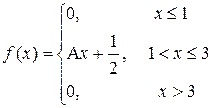
| a =0,5; b=2 |
14. a) На склад поступило 600 м провода, причем высоковольтного из них 100 м диаметром 10 мм; 150 м диаметром 15 мм; 200 м диаметром 25 мм; 50 м диаметром 20 мм; 40 м диаметром 30 мм.
Остальной невысоковольтный. Потребитель заказал высоковольтный провод. Составить закон распределения высоковольтного провода по размеру его диаметра.
P (10≤X≤20)
b)
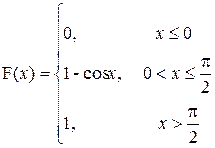
|
a= 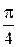 ; b= ; b= 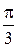
|
15. a) Поезд следует из города А в город В через пункты С и D. Вероятность опоздания на участке АС составляет p1=0,3; на участке CD – p2=0,4; на участке DB – p3=0,35. Пусть X – число участков, на которых может произойти опоздание поезда. Найти закон распределения случайной величины X.
P (0<X≤3)
b)
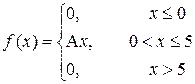
| a =2; b=6 |
16. a) Для ремонта локомотива требуются три детали различного назначения. В цехе три автомата производят эти детали в стандартном качестве с вероятностями 0,9; 0,8; 0,7. Пусть X – количество отобранных стандартных деталей. Найти закон распределения случайной величины X.
P (0≤X<2)
b)
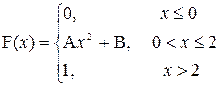
| a=0; b=1 |
17. a)
| x | –2 | –1 | 0 | 1 | 2 |
| p | 0,1 | 0,2 | p | 0,25 | 0,15 |
P (–1≤X<1)
b)
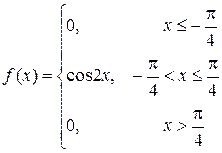
|
a=0; b= 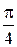
|
34. a)
| x | 1 | 1,5 | 2 | 4 | 5 |
| p | 0,1 | 0,05 | 0,1 | 0,35 | p |
P (1,5≤X≤5)
b)
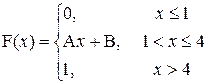
| a=2; b=3 |
19. a) На конкурс предложено 5 проектов прокладки железнодорожной магистрали, из которых может быть принят только один. Проекты по одному проходят предварительное обсуждение. Проект, не прошедший его, из конкурса исключается. Пусть X – число проектов, прошедших предварительное обсуждение. Составить закон распределения случайной величины X.
P (1,5≤X≤3,5)
 b)
b)
| a=0; b=2,5 |
a)
| x | 0 | 1 | 2 | 3 | 4 |
| p | 0,03 | p | 0,3 | 0,35 | 0,1 |
P (1≤X≤3)
b)
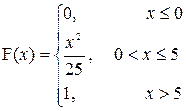
| a=2; b=4 |
21. a) На товарную станцию прибыло 3 партии одинаковых контейнеров по 12 штук в каждой, причем в первой партии 3 нестандартных, во второй – 7, в третьей – 2. Из каждой партии отбираются по одному контейнеру. Составить закон распределения отбора стандартных контейнеров.
P (0,5≤X<2,5)
 b)
b)
| a=1,5; b=2,5 |
22. a)
| x | 1 | 3 | 5 | 7 | 9 |
| p | 0,2 | 0,1 | 0,1 | 0,4 | 0,3 |
P (1≤X≤5)
b)
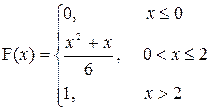
| a=1; b=5 |
23. a) При посадке на электричку пассажир проходит через турникет. Если пассажир без билета, турникет перекрывается. 8 пассажиров стоят в очереди на посадку, из них три без билета. Пусть X – число пассажиров, прошедших турникет до появления первого безбилетника. Составить закон распределения случайной величины X.
P (X≥3)
b)
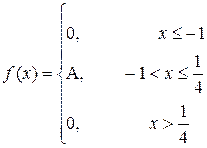
| a= –0,5; b=0,5 |
24. a) В электронной схеме, состоящей из 5 блоков, произошла неисправность в каком-то блоке. Блоки проверяют последовательно один за другим, пока не найдут неисправный блок. Пусть X – номер проверенного блока. Составить закон распределения случайной величины X.
P (1<X<3)
b)
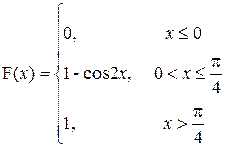
|
a=0; b= 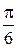
|
25. a)
| x | -3 | -1 | 0 | 1 | 2 |
| p | 0,1 | p | 0,2 | 0,2 | 0,2 |
P (–1,5<X≤1)
 b)
b)
| a=0; b=2 |
26. a)
| x | 0 | 1 | 2 | 3 | 4 |
| p | 0,02 | p | 0,4 | 0,3 | 0,2 |
P (X>3)
b)
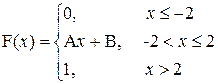
| a= –1; b=0 |
27. a) В цех по ремонту локомотивов поступило 4 партии различных приборов по 10 штук в каждой. Известно, что в каждой партии находится по 4 прибора со знаком качества. Наудачу отбираются по одному прибору из каждой партии. Найти закон распределения количества отобранных приборов со знаком качества.
P (1,5≤X<3,5)
b)
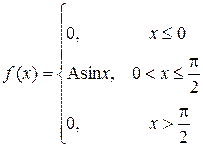
|
a= 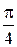 ; b= ; b= 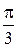
|
28. a) На городские соревнования от железнодорожной спортивной организации отбираются наугад по одному спортсмену от 3-х спортивных групп. В первой группе 10 спортсменов, из них 3 мастера спорта; во второй – 12 спортсменов, из них 4 мастера спорта; в третьей – 20 спортсменов, среди которых 5 мастеров спорта. Пусть X – число отобранных мастеров спорта. Написать закон распределения случайной величины X.
P (X≥1)
b)
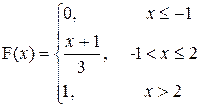
| a= –1; b=0 |
a)
| x | 1 | 2 | 3 | 5 | 7 |
| p | 0,1 | p | 0,3 | 0,35 | 0,15 |
P (2,5≤X<5)
b)
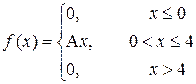
| a=3; b=¥ |
30. a) При подтверждении квалификации машиниста претендент проходит тестирование. Экзаменатор задает 4 вопроса и прекращает тестирование, если претендент не отвечает хотя бы на один вопрос. Пусть X – количество удовлетворительных ответов. Найти закон распределения случайной величины X, если вероятность ответить машинисту на один вопрос равна 0,8.
P (0≤X<2)
b)
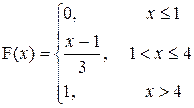
| a=0; b=2 |
Дата: 2019-12-09, просмотров: 324.