Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Оглавление

Оглавление 2

§1. Условие физической задачи. 3

§2. Вывод уравнения колебания струны. 4

§3. Формулировка математической модели. 9

§4. Получение решения методом Фурье. 10

§5. Доказательство достоверности решения, полученного методом Фурье. 14

§6. Вывод конечно-разностных уравнений, формулировка вычислительной схемы метода конечных разностей 16

§7. Табулирование значений искомой функции в узлах сетки, покрывающей область, в которой найдено решение. Построение графика найденной функции. 17

§8. Исследование времени затухания колебания струны из различных материалов в различных средах. 19

§9. Анализ результатов решения задачи. 21

§10. Список использованной литературы и пакетов прикладных программ. 22

Приложение 1. Графики функций отклонения струны и скорости колебания. 23

Приложение 2. Графики функций отклонения струны из различных материалов в различных средах. 25

 

Условие физической задачи

№75(б)

 

Однородная струна длиной , закрепленная на обоих концах, находится в прямолинейном положении равновесия. В некоторый момент времени, принимаемый за начальный, она получает в точке  удар от молоточка, который сообщает этой точке постоянную скорость . Найти отклонение струны для любого момента времени.

       Струна возбуждается начальной скоростью

                  

       Этот случай соответствует плоскому жесткому молоточку, имеющему ширину , такой молоточек в центре интервала возбуждает максимальную скорость.

 

 

Задание на исследование

Исследовать продолжительность процесса колебания для двух материалов струны (с сильными и слабыми упругими свойствами) и для двух сред (с высокой и низкой вязкостью). Определить  время , при котором .

§2. Вывод уравнения колебания струны [2]

 

Пусть конеч­ные точки струны закреплены, а сама струна туго натянута. Если вывести струну из положения равновесия (например, оттянуть ее или ударить по ней), то струна начнет коле­баться. Будем предполагать, что все точки струны движутся перпендикулярно ее положению равновесия (поперечные коле­бания), причем в каждый момент времени струна лежит в одной и той же плоскости.

Возьмем в этой плоскости систему прямоугольных коор­динат . Тогда, если в начальный момент времени струна располагалась вдоль оси , то  будет означать отклонение струны от положения равновесия. В процессе колебания ве­личина отклонения бу­дет зависеть от абсциссы точки струны  и от вре­мени .

 

Таким образом, чтобы знать положение любой точки струны в произвольный момент времени, нам надо найти зависимость  от  и , т. е. найти функцию . При каждом фиксированном значении t график функции  представляет форму колеблющейся струны в момент времени  (рис. 1), частная  производная    дает при этом угловой коэффициент касательной в точке с абсциссой . При изменении  форма струны, очевидно, изменяется, и, чтобы представить себе процесс колебаний, мы должны построить несколько гра­фиков функции  при различных значениях , т. е. сделать несколько мгновенных снимков колеблющейся струны. При постоянном значении  функция дает закон дви­жения точки с абсциссой   вдоль прямой, параллельной оси , производная - скорость этого движения,
а вторая производная - ускорение.

Наша задача состоит в том, чтобы составить уравнение, которому должна удовлетворять функция . Для этого сделаем предварительно несколько упрощающих предположе­ний. Будем считать струну абсолютно гибкой, т.е. не сопротивляющейся изгибу; это означает, что если удалить часть струны, лежащую по одну сторону от какой-либо ее точки, то сила натяжения , заменяющая действие удаленной части, всегда будет направлена по касательной к струне (рис. 1). Струна предполагается упругой и подчиняющейся закону Гука; изменение величины силы натяжения при этом пропорционально изменению длины струны. Примем, что струна однородна; линейную плотность ее обозначим бук­вой  ( —масса единицы длины струны).

Предположим, далее, что на струну в плоскости колеба­ния действуют силы, параллельные оси , которые могут меняться вдоль струны и со временем. Силы эти будем счи­тать непрерывно распределенными вдоль струны; величину силы, направленной вверх, условимся считать положительной, а вниз - отрицательной. Плотность распределения этих сил вдоль струны является функцией абсциссы  и времени ; обозначим ее через . Если, в частности, единствен­ной внешней силой является вес струны, то , где —плотность струны, — ускорение силы тяжести. Силами сопротивления среды, в которой колеблется струна, мы пока пренебрегаем.

Мы будем изучать только малые колебания струны. Если обозначить через острый угол между осью абсцисс и касательной к струне в точке с абсциссой х в момент времени , то условие малости колебаний заключается в том, что величиной  можно пренебрегать:

 

(1.1)

 

Поскольку разложение функции  в ряд Маклорена имеет вид   

то в силу условия (1.1) можно считать, что

	(1.2)
Далее, , и, следовательно,	(1.3)
И наконец,  и	(1.4)
Так как , то в си­лу полученных условий заклю­чаем, что	(1.5)

 

Отсюда сразу следует, что в процессе колебания мы можем пренебречь изменением длины любого участка струны. Действительно, длина участка  в момент времени  (рис. 2) равна

 

	(1.6)
Согласно (1.5) заключаем, что	(1.7)

     

 

Покажем теперь, что при наших предположениях вели­чину силы натяжения  можно считать постоянной, не зависящей ни от точки ее приложения, ни от вре­мени . Возьмем для этого какой-либо участок струны  (рис. 3).

 

В момент времени  заменим действие отброшен­ных участков силами натяжений  и . Так как по усло­вию все точки струны движутся параллельно оси  и внешние силы также параллельны этой оси, то сумма проек­ций сил натяжения на ось должна равняться нулю:

 

(1.8)

 

Отсюда в силу (1.3) заключаем, что . Так как точки  и  выбраны произвольно, то это и доказывает, что в данный момент времени силы натяжения во всех точках равны между собой.

Поскольку мы пренебрегаем изменением длины любого участка струны, то в силу закона Гука неизменным остается и натяжение струны. Итак, мы показали, что в пределах выбранной точности Т есть величина постоянная:

 

.

(1.9)

 

Перейдем теперь к выводу уравнения колебаний струны. Выделим бесконечно малый участок струны , проекти­рующийся в промежуток  оси абсцисс (рис. 4). На него действуют силы натяжения  и , заменяющие влияние отброшенных частей струны. Как уже отмечалось выше, силы  и  направлены по касательным к струне в точках  и ; величина этих сил постоянно равна . Согласно равенству (1.8) сумма проекций сил  и  на ось  равна нулю. Вычислим сумму проекций этих же сил на ось :

В силу (1.4) можно записать, что

Следовательно,

 

(1.10)

Здесь мы заменили частное приращение производной  при переходе от аргументов  к аргументам  ее частным дифференциалом, т. е. .

Примечание. Если бы участок струны  располагался, как на рис. 2, то сумма проекций сил  и  равнялась бы ; но теперь   и в результате мы снова получили бы формулу (1.10).

Равнодействующую внешних сил, приложенных к участку  в момент времени , обозначим через . Согласно определению функции  и приближенному равенству (1.7) можно считать, что

 

(1.11)

 

Направление равнодействующей  определится знаком функции  (направление  на рис. 4 соответствует случаю ).

После того как найдены все силы, действующие на участок , применим к нему второй закон Ньютона, согласно которому произведение массы на ускорение равно сумме всех действующих сил (в силу малости участка  мы рассматриваем его просто как материальную точку).

Так как масса участка  струны равна , то, используя формулы (1.10) и (1.11), получим

Сократив на  и разделив все члены равенства на , приведем полученное уравнение к виду

(1.12)

(  положительная постоянная величина). В результате мы получили линейное дифференциальное уравнение с частными производными второго порядка с постоянными коэффициентами. Уравнение (1.12) называется уравнением колебаний струны или одномерным волновым уравнением. Это одно из простейших и в то же время важнейших дифференциальных уравнений математической физики. Как мы позже увидим, к нему сводится не только рассматриваемая задача, но и многие другие.

Если , уравнение (1.12) называется однородным; оно описывает свободные колебания струны без воздействия внешних усилий.

Если  тождественно не равно нулю, то уравнение называется неоднородным, в этом случае рассматриваются вынужденные колебания струны. Когда на струну действуют только силы тяжести, а натяжение струны  велико, мы вправе пренебречь вторым слагаемым в правой части уравнения струны по сравнению с первым и рассматривать, таким образом, колебания струны как свободные.

 

Рассмотрим теперь слу­чай, когда колебания струны происходят при наличии сопро­тивления среды. Силу сопротивления, возникающую при этом, примем пропорциональной скорости движения (такой же закон для силы сопротивления принимается и при изучении гармонических ко­лебаний точки). Тогда на бесконечно малый участок струны  (рис. 4) действует сила

 

(1.13)

 

где  — коэффициент пропорциональности. Рассуждая так же, как при выводе уравнения

(1.12), и учитывая, что сила сопротивления всегда направлена против движения, придем к уравнению

 

(1.14)

 

где введено обозначение . Ограничиваясь случаем свободных колебаний, запишем уравнение (1.14) в виде

 

(1.15)

         

Список использованной литературы и пакетов прикладных программ.

1. Mathematica 5 © Copyright 1988-2003 Wolfram Research, Inc.

2. Араманович И.Г., Левин В.И. Уравнения математической физики: Учеб. для втузов: - М. : Издательство Наука, 1969. – 288 с.

3. Евграфова Н.Н., Каган. В.Л. Курс физики: Учеб пособие для подготовительных отделения вузов -. 2-е изд. –М.: Высш. школа, 1978 .- 512 с.

4. Чертов А.Г., Воробьев А.А. Задачник по физике: Учеб пособие для втузов .- 7-е изд., перераб. и доп. –М.: Издательство Физико-математической литературы, 2001 .- 640с.

5. Уравнения математической физики © Copyright 2005 Голубев В.О.

Приложение 1. Графики функций отклонения струны и скорости колебания.

 

Управляемые параметры , , , , , , ::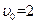

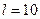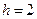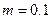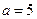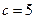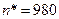Интервалы изменения переменных 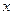 и :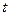

 

 

 

 

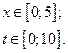
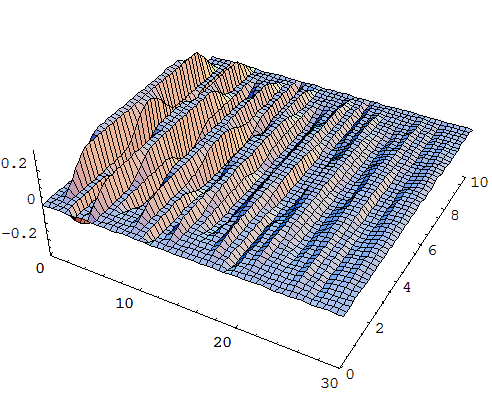
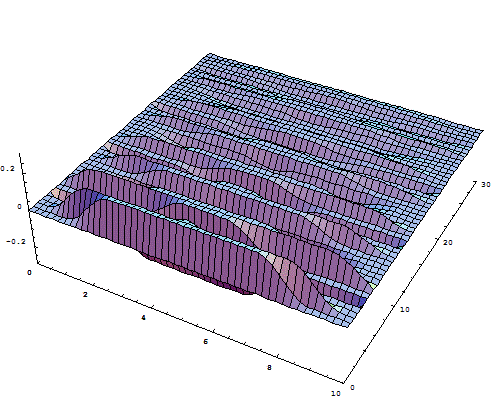
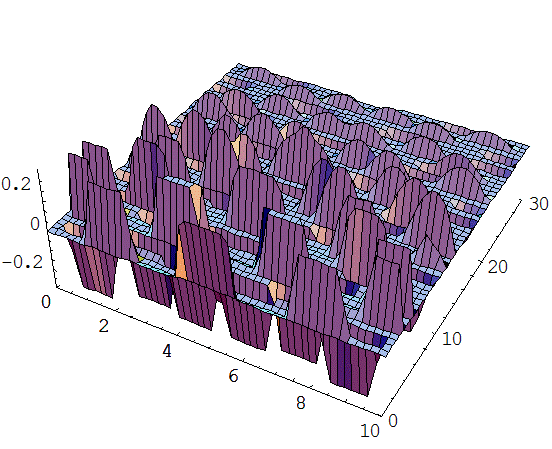
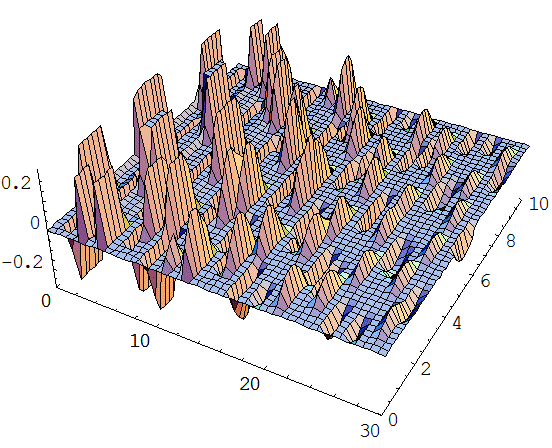
Приложение 2. Графики функций отклонения струны из различных материалов в различных средах.

 

Случай вода – железо:

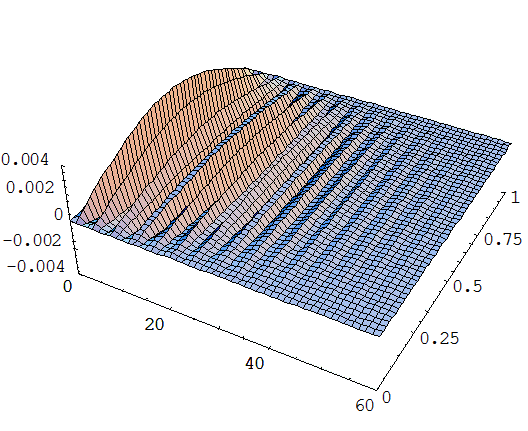
Случай вода – алюминий:

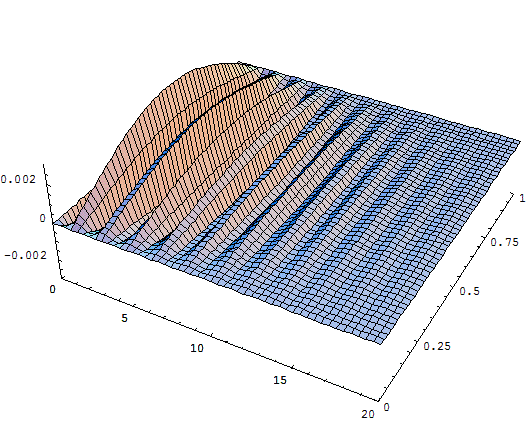
Случай машинное масло – железо:

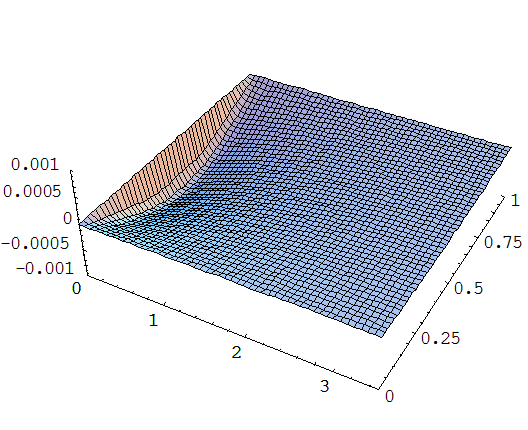
Случай машинное масло – алюминий:

 

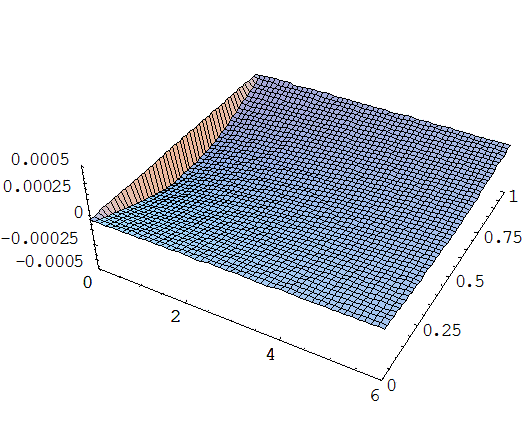
Оглавление

Оглавление 2

§1. Условие физической задачи. 3

§2. Вывод уравнения колебания струны. 4

§3. Формулировка математической модели. 9

§4. Получение решения методом Фурье. 10

§5. Доказательство достоверности решения, полученного методом Фурье. 14

§6. Вывод конечно-разностных уравнений, формулировка вычислительной схемы метода конечных разностей 16

§7. Табулирование значений искомой функции в узлах сетки, покрывающей область, в которой найдено решение. Построение графика найденной функции. 17

§8. Исследование времени затухания колебания струны из различных материалов в различных средах. 19

§9. Анализ результатов решения задачи. 21

§10. Список использованной литературы и пакетов прикладных программ. 22

Приложение 1. Графики функций отклонения струны и скорости колебания. 23

Приложение 2. Графики функций отклонения струны из различных материалов в различных средах. 25

 

Условие физической задачи

№75(б)

 

Однородная струна длиной , закрепленная на обоих концах, находится в прямолинейном положении равновесия. В некоторый момент времени, принимаемый за начальный, она получает в точке  удар от молоточка, который сообщает этой точке постоянную скорость . Найти отклонение струны для любого момента времени.

       Струна возбуждается начальной скоростью

                  

       Этот случай соответствует плоскому жесткому молоточку, имеющему ширину , такой молоточек в центре интервала возбуждает максимальную скорость.

 

 

Задание на исследование

Исследовать продолжительность процесса колебания для двух материалов струны (с сильными и слабыми упругими свойствами) и для двух сред (с высокой и низкой вязкостью). Определить  время , при котором .

§2. Вывод уравнения колебания струны [2]

 

Пусть конеч­ные точки струны закреплены, а сама струна туго натянута. Если вывести струну из положения равновесия (например, оттянуть ее или ударить по ней), то струна начнет коле­баться. Будем предполагать, что все точки струны движутся перпендикулярно ее положению равновесия (поперечные коле­бания), причем в каждый момент времени струна лежит в одной и той же плоскости.

Возьмем в этой плоскости систему прямоугольных коор­динат . Тогда, если в начальный момент времени струна располагалась вдоль оси , то  будет означать отклонение струны от положения равновесия. В процессе колебания ве­личина отклонения бу­дет зависеть от абсциссы точки струны  и от вре­мени .

 

Таким образом, чтобы знать положение любой точки струны в произвольный момент времени, нам надо найти зависимость  от  и , т. е. найти функцию . При каждом фиксированном значении t график функции  представляет форму колеблющейся струны в момент времени  (рис. 1), частная  производная    дает при этом угловой коэффициент касательной в точке с абсциссой . При изменении  форма струны, очевидно, изменяется, и, чтобы представить себе процесс колебаний, мы должны построить несколько гра­фиков функции  при различных значениях , т. е. сделать несколько мгновенных снимков колеблющейся струны. При постоянном значении  функция дает закон дви­жения точки с абсциссой   вдоль прямой, параллельной оси , производная - скорость этого движения,
а вторая производная - ускорение.

Наша задача состоит в том, чтобы составить уравнение, которому должна удовлетворять функция . Для этого сделаем предварительно несколько упрощающих предположе­ний. Будем считать струну абсолютно гибкой, т.е. не сопротивляющейся изгибу; это означает, что если удалить часть струны, лежащую по одну сторону от какой-либо ее точки, то сила натяжения , заменяющая действие удаленной части, всегда будет направлена по касательной к струне (рис. 1). Струна предполагается упругой и подчиняющейся закону Гука; изменение величины силы натяжения при этом пропорционально изменению длины струны. Примем, что струна однородна; линейную плотность ее обозначим бук­вой  ( —масса единицы длины струны).

Предположим, далее, что на струну в плоскости колеба­ния действуют силы, параллельные оси , которые могут меняться вдоль струны и со временем. Силы эти будем счи­тать непрерывно распределенными вдоль струны; величину силы, направленной вверх, условимся считать положительной, а вниз - отрицательной. Плотность распределения этих сил вдоль струны является функцией абсциссы  и времени ; обозначим ее через . Если, в частности, единствен­ной внешней силой является вес струны, то , где —плотность струны, — ускорение силы тяжести. Силами сопротивления среды, в которой колеблется струна, мы пока пренебрегаем.

Мы будем изучать только малые колебания струны. Если обозначить через острый угол между осью абсцисс и касательной к струне в точке с абсциссой х в момент времени , то условие малости колебаний заключается в том, что величиной  можно пренебрегать:

 

(1.1)

 

Поскольку разложение функции  в ряд Маклорена имеет вид   

то в силу условия (1.1) можно считать, что

	(1.2)
Далее, , и, следовательно,	(1.3)
И наконец,  и	(1.4)
Так как , то в си­лу полученных условий заклю­чаем, что	(1.5)

 

Отсюда сразу следует, что в процессе колебания мы можем пренебречь изменением длины любого участка струны. Действительно, длина участка  в момент времени  (рис. 2) равна

 

	(1.6)
Согласно (1.5) заключаем, что	(1.7)

     

 

Покажем теперь, что при наших предположениях вели­чину силы натяжения  можно считать постоянной, не зависящей ни от точки ее приложения, ни от вре­мени . Возьмем для этого какой-либо участок струны  (рис. 3).

 

В момент времени  заменим действие отброшен­ных участков силами натяжений  и . Так как по усло­вию все точки струны движутся параллельно оси  и внешние силы также параллельны этой оси, то сумма проек­ций сил натяжения на ось должна равняться нулю:

 

(1.8)

 

Отсюда в силу (1.3) заключаем, что . Так как точки  и  выбраны произвольно, то это и доказывает, что в данный момент времени силы натяжения во всех точках равны между собой.

Поскольку мы пренебрегаем изменением длины любого участка струны, то в силу закона Гука неизменным остается и натяжение струны. Итак, мы показали, что в пределах выбранной точности Т есть величина постоянная:

 

.

(1.9)

 

Перейдем теперь к выводу уравнения колебаний струны. Выделим бесконечно малый участок струны , проекти­рующийся в промежуток  оси абсцисс (рис. 4). На него действуют силы натяжения  и , заменяющие влияние отброшенных частей струны. Как уже отмечалось выше, силы  и  направлены по касательным к струне в точках  и ; величина этих сил постоянно равна . Согласно равенству (1.8) сумма проекций сил  и  на ось  равна нулю. Вычислим сумму проекций этих же сил на ось :

В силу (1.4) можно записать, что

Следовательно,

 

(1.10)

Здесь мы заменили частное приращение производной  при переходе от аргументов  к аргументам  ее частным дифференциалом, т. е. .

Примечание. Если бы участок струны  располагался, как на рис. 2, то сумма проекций сил  и  равнялась бы ; но теперь   и в результате мы снова получили бы формулу (1.10).

Равнодействующую внешних сил, приложенных к участку  в момент времени , обозначим через . Согласно определению функции  и приближенному равенству (1.7) можно считать, что

 

(1.11)

 

Направление равнодействующей  определится знаком функции  (направление  на рис. 4 соответствует случаю ).

После того как найдены все силы, действующие на участок , применим к нему второй закон Ньютона, согласно которому произведение массы на ускорение равно сумме всех действующих сил (в силу малости участка  мы рассматриваем его просто как материальную точку).

Так как масса участка  струны равна , то, используя формулы (1.10) и (1.11), получим

Сократив на  и разделив все члены равенства на , приведем полученное уравнение к виду

(1.12)

(  положительная постоянная величина). В результате мы получили линейное дифференциальное уравнение с частными производными второго порядка с постоянными коэффициентами. Уравнение (1.12) называется уравнением колебаний струны или одномерным волновым уравнением. Это одно из простейших и в то же время важнейших дифференциальных уравнений математической физики. Как мы позже увидим, к нему сводится не только рассматриваемая задача, но и многие другие.

Если , уравнение (1.12) называется однородным; оно описывает свободные колебания струны без воздействия внешних усилий.

Если  тождественно не равно нулю, то уравнение называется неоднородным, в этом случае рассматриваются вынужденные колебания струны. Когда на струну действуют только силы тяжести, а натяжение струны  велико, мы вправе пренебречь вторым слагаемым в правой части уравнения струны по сравнению с первым и рассматривать, таким образом, колебания струны как свободные.

 

Рассмотрим теперь слу­чай, когда колебания струны происходят при наличии сопро­тивления среды. Силу сопротивления, возникающую при этом, примем пропорциональной скорости движения (такой же закон для силы сопротивления принимается и при изучении гармонических ко­лебаний точки). Тогда на бесконечно малый участок струны  (рис. 4) действует сила

 

(1.13)

 

где  — коэффициент пропорциональности. Рассуждая так же, как при выводе уравнения

(1.12), и учитывая, что сила сопротивления всегда направлена против движения, придем к уравнению

 

(1.14)

 

где введено обозначение . Ограничиваясь случаем свободных колебаний, запишем уравнение (1.14) в виде

 

(1.15)

         

Формулировка математической модели

1. Найти функцию , удовлетворяющую ДУЧП , где

 - константы по  и , зависящие от физических свойств материала и среды;

- координата точки на струне;

 - время от начального момента;

 - функция, показывающая отклонение точки  от положения равновесия в момент времени .

2. Независимые переменные  и  изменяются в области .

3. Начальные условия для функции :

.

4. Граничные условия для функции :  и .

 

Таким образом, математической моделью поставленной задачи является краевая задача Дирихле для одномерного волнового уравнения (ДУЧП гиперболического типа).